应用多元统计分析习题解答 第九章
- 格式:docx
- 大小:199.28 KB
- 文档页数:5

2.1.试叙述多元联合分布和边际分布之间的关系。
解:多元联合分布讨论多个随机变量联合到一起的概率分布状况,12(,,)p X X X X '=L 的联合分布密度函数是一个p 维的函数,而边际分布讨论是12(,,)p X X X X '=L 的子向量的概率分布,其概率密度函数的维数小于p 。
2.2设二维随机向量12()X X '服从二元正态分布,写出其联合分布。
解:设12()X X '的均值向量为()12μμ'=μ,协方差矩阵为21122212σσσσ⎛⎫ ⎪⎝⎭,则其联合分布密度函数为1/21222112112222122121()exp ()()2f σσσσσσσσ--⎧⎫⎛⎫⎛⎫⎪⎪'=---⎨⎬ ⎪⎪⎝⎭⎝⎭⎪⎪⎩⎭x x μx μ。
2.3已知随机向量12()X X '的联合密度函数为121212222[()()()()2()()](,)()()d c x a b a x c x a x c f x x b a d c --+-----=--其中1ax b ≤≤,2c x d ≤≤。
求(1)随机变量1X 和2X 的边缘密度函数、均值和方差; (2)随机变量1X 和2X 的协方差和相关系数;(3)判断1X 和2X 是否相互独立。
(1)解:随机变量1X 和2X 的边缘密度函数、均值和方差;112121222[()()()()2()()]()()()dx cd c x a b a x c x a x c f x dx b a d c --+-----=--⎰12212222222()()2[()()2()()]()()()()dd c c d c x a x b a x c x a x c dx b a d c b a d c -------=+----⎰ 121222202()()2[()2()]()()()()dd c c d c x a x b a t x a t dt b a d c b a d c ------=+----⎰ 2212122222()()[()2()]1()()()()d cdc d c x a x b a t x a t b a d c b a d c b a------=+=----- 所以 由于1X 服从均匀分布,则均值为2b a+,方差为()212b a -。

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS 提供的绘制散点图功能进行一元线性回归分析。
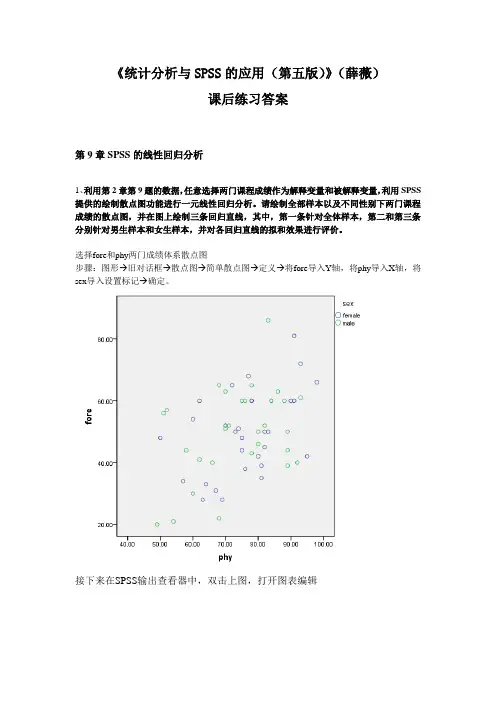
请绘制全部样本以及不同性别下两门课程成绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤:图形→旧对话框→散点图→简单散点图→定义→将fore导入Y轴,将phy导入X轴,将sex导入设置标记→确定。
接下来在SPSS输出查看器中,双击上图,打开图表编辑在图表编辑器中,选择“元素”菜单→选择总计拟合线→选择线性→应用→再选择元素菜单→点击子组拟合线→选择线性→应用。
分析:如上图所示,通过散点图,被解释变量y(即:fore)与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的?相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以及相关方向和程度做出正确判断之前,就进行回归分析,很容易造成“虚假回归”。
与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种,研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。
3、请说明为什么需要对线性回归方程进行统计检验?一般需要对哪些方面进行检验?检验其可信程度并找出哪些变量的影响显著、哪些不显著。


第9章多元线性回归习题答案多元线性回归第9章教材习题答案9.1 根据下面的数据用Excel进行回归,并对回归结果进行讨论,计算、时y 的预测值。
xy x213 174 129 18 2814 31 1898 28 2029 149 5212 47 1885 215 3811 22 1508 36 167513517详细答案:由Excel输出的回归结果如下:回归统计Multiple R 0.4592340.210896 R SquareAdjusted R Square-0.0145613.34122标准误10观测方差分Significance FMSSSFdf0.4364850.93541332.98372166.4919回归分1245.916177.9887残1578.99总CoefficientsUpper 95%P-valueLower 95%t Stat标准误25.028777.7092822.278630.298298Intercept-27.65191.12344-0.049710.653301X Variable 10.1059920.200918-0.30035-0.469041.9281691.47216X Variable 20.231624-1.552941.3097555.409276得到的回证方程为:。
表示,在不变的条不变的条件每变化一个单位件下,,y平均下示表,在降0.04971个单位;每变化一个单位,下,y 平均增加1.928169个单位。
,表示在因变量y的变差中能够被y与和判定系数之间的线性关系所解释的比例为21.09%。
由于这一比例很低,表明回归方程的拟合程度很差。
估计标准误差,预测误差也较大。
方差分析表显示,Significance F=0.436485>a=0.05,表明y与和之间的线性关系不显著。
著显不均数系归回个两,a=0.05于大均值P的验检数系归回于用.当=200、=7时,y的预测值为:9.2 根据下面Excel输出的回归结果,说明模型中涉及多少个自变量?多少个观察值?写出回归方程,并根据F、、及调整的的值对模型进行讨论。
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS 提供的绘制散点图功能进行一元线性回归分析。
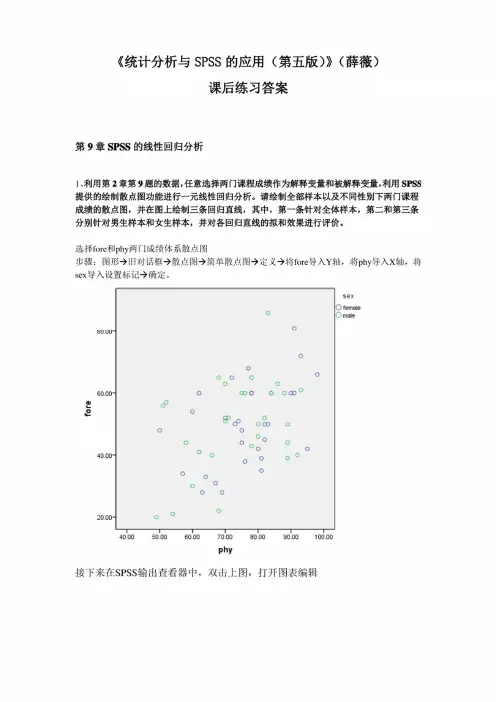
请绘制全部样本以及不同性别下两门课程成绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤:图形今旧对话框今散点图今简单散点图今定义分将fore导入Y轴,将phy导入X轴,将sex导入设置标记今确定。
sexO femaleOrnateOU.UU-60.00-40.00-20.00-40.0050.0060.0070.0080.0090.00100.00phy接下来在SPSS输出查看器中,双击上图,打开图表编辑今点击子组拟合线今选择线性3应用。
分析:如上图所示,通过散点图,被解释变量y(即:fore)与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的?相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以及相关方向和程度做出正确判断之前,就进行回归分析,很容易造成“虚假回归”。
与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种,研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。

一、填空题:1、多元统计剖析是运用数理统计方法来研究解决多指标问题的理论和方法 .2、回归参数明显性查验是查验解说变量对被解说变量的影响能否著.3、聚类剖析就是剖析怎样对样品(或变量)进行量化分类的问题。
往常聚类分析分为Q型聚类和R型聚类。
4、相应剖析的主要目的是追求列联表行要素A和列要素B的基本剖析特点和它们的最优联立表示。
5、因子剖析把每个原始变量分解为两部分要素:一部分为公共因子,另一部分为特别因子。
6、若x( ): N P( ,),=1,2,3 .n且互相独立,则样本均值向量x 听从的散布为 _ x ~N(μ,Σ /n)_。
二、简答1、简述典型变量与典型有关系数的观点,并说明典型有关剖析的基本思想。
在每组变量中找出变量的线性组合,使得两组的线性组合之间拥有最大的有关系数。
选用和最先精选的这对线性组合不有关的线性组合,使其配对,并选用有关系数最大的一对,这样下去直到两组之间的有关性被提取完成为止。
被选出的线性组合配对称为典型变量,它们的有关系数称为典型有关系数。
2、简述相应剖析的基本思想。
相应剖析,是指对两个定性变量的多种水平进行剖析。
设有两组要素A和B,此中要素 A 包括 r 个水平,要素 B 包括 c 个水平。
对这两组要素作随机抽样检查,获得一个 rc 的二维列联表,记为。
要追求列联表列要素 A 和行要素 B 的基本剖析特点和最优列联表示。
相应剖析即是经过列联表的变换,使得要素 A和要素 B 拥有平等性,进而用同样的因子轴同时描绘两个要素各个水平的情况。
把两个要素的各个水平的情况同时反应到拥有同样坐标轴的因子平面上,进而获得要素 A 、 B 的联系。
3、简述费希尔鉴别法的基本思想。
从 k 个整体中抽取拥有 p 个指标的样品观察数据,借助方差剖析的思想结构一个线性鉴别函数系数:确立的原则是使得整体之间差别最大,而使每个整体内部的离差最小。
将新样 品的 p 个指标值代入线性鉴别函数式中求出 值,而后依据鉴别必定的规则,就能够鉴别新的样品属于哪个整体。


一、填空题:1、多元统计分析是运用数理统计方法来研究解决多指标问题的理论和方法.2、回归参数显著性检验是检验解释变量对被解释变量的影响是否著.3、聚类分析就是分析如何对样品(或变量)进行量化分类的问题。
通常聚类分析分为 Q型聚类和R型聚类。
4、相应分析的主要目的是寻求列联表行因素A 和列因素B 的基本分析特征和它们的最优联立表示。
5、因子分析把每个原始变量分解为两部分因素:一部分为公共因子,另一部分为特殊因子。
6、若()(,), Px N αμα∑=1,2,3….n且相互独立,则样本均值向量x服从的分布为_x~N(μ,Σ/n)_。
二、简答1、简述典型变量与典型相关系数的概念,并说明典型相关分析的基本思想。
在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数。
选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的一对,如此下去直到两组之间的相关性被提取完毕为止。
被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数。
2、简述相应分析的基本思想。
相应分析,是指对两个定性变量的多种水平进行分析。
设有两组因素A和B,其中因素A包含r个水平,因素B包含c个水平。
对这两组因素作随机抽样调查,得到一个rc的二维列联表,记为。
要寻求列联表列因素A和行因素B 的基本分析特征和最优列联表示。
相应分析即是通过列联表的转换,使得因素A 和因素B具有对等性,从而用相同的因子轴同时描述两个因素各个水平的情况。
把两个因素的各个水平的状况同时反映到具有相同坐标轴的因子平面上,从而得到因素A 、B 的联系。
3、简述费希尔判别法的基本思想。
从k 个总体中抽取具有p 个指标的样品观测数据,借助方差分析的思想构造一个线性判别函数 系数:确定的原则是使得总体之间区别最大,而使每个总体内部的离差最小。
将新样品的p 个指标值代入线性判别函数式中求出 值,然后根据判别一定的规则,就可以判别新的样品属于哪个总体。

第1章 多元正态分布1、在数据处理时,为什么通常要进行标准化处理?数据的标准化是将数据按比例缩放,使之落入一个小的特定区间。
在某些比较和评价的指标处理中经常会用到,去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或量级的指标能够进行比较和加权。
其中最典型的就是0-1标准化和Z 标准化。
2、欧氏距离与马氏距离的优缺点是什么?欧氏距离也称欧几里得度量、欧几里得度量,是一个通常采用的距离定义,它是在m 维空间中两个点之间的真实距离。
在二维和三维空间中的欧氏距离的就是两点之间的距离。
缺点:就大部分统计问题而言,欧氏距离是不能令人满意的。
每个坐标对欧氏距离的贡献是同等的。
当坐标表示测量值时,它们往往带有大小不等的随机波动,在这种情况下,合理的方法是对坐标加权,使变化较大的坐标比变化较小的坐标有较小的权系数,这就产生了各种距离。
当各个分量为不同性质的量时,“距离”的大小与指标的单位有关。
它将样品的不同属性之间的差别等同看待,这一点有时不能满足实际要求。
没有考虑到总体变异对距离远近的影响。
马氏距离表示数据的协方差距离。
为两个服从同一分布并且其协方差矩阵为Σ的随机变量与的差异程度:如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离。
优点:它不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关。
由标准化数据和中心化数据计算出的二点之间的马氏距离相同。
马氏距离还可以排除变量之间的相关性的干扰。
缺点:夸大了变化微小的变量的作用。
受协方差矩阵不稳定的影响,马氏距离并不总是能顺利计算出。
3、当变量X1和X2方向上的变差相等,且与互相独立时,采用欧氏距离与统计距离是否一致?统计距离区别于欧式距离,此距离要依赖样本的方差和协方差,能够体现各变量在变差大小上的不同,以及优势存在的相关性,还要求距离与各变量所用的单位无关。
如果各变量之间相互独立,即观测变量的协方差矩阵是对角矩阵, 则马氏距离就退化为用各个观测指标的标准差的倒数作为权数的加权欧氏距离。
可编辑修改精选全文完整版应用统计学第9章分类数据分析9.1 欲研究不同收入群体对某种特定上坡是否有相同的购买习惯,市场研究人员调查了四个不同收入组的消费者共527人,购买习惯分为:经常购买,不购买,有时购买。
调查结果如下表所示。
要求:(1)提出假设。
χ值。
(2)计算2(3)以α=0.1的显著水平进行检验。
解:(1):提出假设:oH:不同收入群体对某种特定商品的购买习惯相同H不同收入群体对某种特定商品的购买习惯不全相同1:(2):χ计算结果3⨯4列联表期望值及22()2fo fe feχ=-÷=∑17.63所以2χ的值为17.63.(3):α=0.1 自由度(31)(41)6df=-⨯-=临界值χ0.1²(6)=10.64 2χ=17.63>χ0.1²(6)=10.64∴拒绝原假设,接受备择假设。
结论:不同收入群体对某种特定商品的购买习惯不全相同9.4 教学改革后学生有了更多的选课自由,但学院领导在安排课程上也面临新的问题。
例如MBA研究生班的学生选课学年之间的变化常常很大,去年的学生很多人选会计课,而今年的学生很多人选市场营销课。
由于事先无法确定究竟有多少学生选各门课程,所以无法有效地进行教学资源的准备。
由于有人提出学生所选课程与其本科所学的专业有关。
为此学院(1)以0.05的显著性水平检验学生本科所学专业是否影响其读MBA期间所选的课程。
(2)计算P值。
解:4⨯3列联表期望值及2χ计算结果2()2fo fe feχ=-÷=∑14.93提出假设:oH:本科学生所学专业受其读MBA期间所选的课程影响1:H本科学生所学专业不受其读MBA期间所选的课程影响α=0.05 自由度(41)(31)6df=-⨯-=临界值χ0.05²(6)=12.59 2χ=14.93>χ0.05²(6)=12.59∴拒绝原假设,接受备择假设。
结论:本科学生所学专业不受其读MBA期间所选的课程影响(2):利用Excel计算得出P=0.1856。
第二章2.1.试叙述多元联合分布和边际分布之间的关系。
解:多元联合分布讨论多个随机变量联合到一起的概率分布状况,12(,,)p X X X X '=的联合分布密度函数是一个p 维的函数,而边际分布讨论是12(,,)p X X X X '=的子向量的概率分布,其概率密度函数的维数小于p 。
2.2设二维随机向量12()X X '服从二元正态分布,写出其联合分布。
解:设12()X X '的均值向量为()12μμ'=μ,协方差矩阵为21122212σσσσ⎛⎫ ⎪⎝⎭,则其联合分布密度函数为1/21222112112222122121()exp ()()2f σσσσσσσσ--⎧⎫⎛⎫⎛⎫⎪⎪'=---⎨⎬ ⎪⎪⎝⎭⎝⎭⎪⎪⎩⎭x x μx μ。
2.3已知随机向量12()X X '的联合密度函数为121212222[()()()()2()()](,)()()d c x a b a x c x a x c f x x b a d c --+-----=--其中1a x b ≤≤,2c x d ≤≤。
求(1)随机变量1X 和2X 的边缘密度函数、均值和方差; (2)随机变量1X 和2X 的协方差和相关系数; (3)判断1X 和2X 是否相互独立。
(1)解:随机变量1X 和2X 的边缘密度函数、均值和方差;112121222[()()()()2()()]()()()dx cd c x a b a x c x a x c f x dx b a d c --+-----=--⎰12212222222()()2[()()2()()]()()()()dd cc d c x a x b a x c x a x c dx b a d c b a d c -------=+----⎰ 12122222()()2[()2()]()()()()dd cc d c x a x b a t x a t dt b a d c b a d c ------=+----⎰2212122222()()[()2()]1()()()()d cdcd c x a x b a t x a t b a d c b a d c b a------=+=----- 所以由于1X 服从均匀分布,则均值为2b a +,方差为()212b a -。
第二章2.1.试叙述多元联合分布和边际分布之间的关系。
解:多元联合分布讨论多个随机变量联合到一起的概率分布状况,12(,,)p X X X X '=的联合分布密度函数是一个p 维的函数,而边际分布讨论是12(,,)p X X X X '=的子向量的概率分布,其概率密度函数的维数小于p 。
2.2设二维随机向量12()X X '服从二元正态分布,写出其联合分布。
解:设12()X X '的均值向量为()12μμ'=μ,协方差矩阵为21122212σσσσ⎛⎫ ⎪⎝⎭,则其联合分布密度函数为1/21222112112222122121()exp ()()2f σσσσσσσσ--⎧⎫⎛⎫⎛⎫⎪⎪'=---⎨⎬ ⎪⎪⎝⎭⎝⎭⎪⎪⎩⎭x x μx μ。
2.3已知随机向量12()X X '的联合密度函数为121212222[()()()()2()()](,)()()d c x a b a x c x a x c f x x b a d c --+-----=--其中1a x b ≤≤,2c x d ≤≤。
求(1)随机变量1X 和2X 的边缘密度函数、均值和方差; (2)随机变量1X 和2X 的协方差和相关系数; (3)判断1X 和2X 是否相互独立。
(1)解:随机变量1X 和2X 的边缘密度函数、均值和方差;112121222[()()()()2()()]()()()dx cd c x a b a x c x a x c f x dx b a d c --+-----=--⎰12212222222()()2[()()2()()]()()()()dd cc d c x a x b a x c x a x c dx b a d c b a d c -------=+----⎰ 12122222()()2[()2()]()()()()dd cc d c x a x b a t x a t dt b a d c b a d c ------=+----⎰2212122222()()[()2()]1()()()()d cdcd c x a x b a t x a t b a d c b a d c b a------=+=----- 所以由于1X 服从均匀分布,则均值为2b a +,方差为()212b a -。
第九章典型相关分析9. 1什么是典型相关分析?简述其基本思想。
答:典型相关分析是研究两组变最之间相关关系的一种多元统计方法。
用于揭示两组变最之间的内在联系。
典型相关分析的目的是识别并鼠化两组变最之间的联系。
将两组变最相关关系的分析转化为一组变量的线性组合与另一组变量线性组合之间的相关关系。
基本思想:(1)在每组变最中找出变最的线性组合,使得两组的线性组合之间具有最大的相关系数。
即:若设疋)=(卍),材),・・・,疋))、伙〉=(普),疋)厂,曙〉)是两组相互关联的随机变量, 分别在两组变量中选取若干有代表性的综合变最Ui、Vi,使是原变最的线性组合。
u; = 3严秽)+破材)+•••+膚X? 口於X0)Y=附百耳+叩呂习+・・・+曙住)□ b(1),x(2)在D(a(iy X⑴)= D(b⑴‘X(2)) = 1的条件下,使得p(a(ir X(1),b(ir X(2))达到绘人。
(2)选取和最初挑选的这对线性组介不相关的线性组介,使其配对,并选取相关系数最大的一对。
(3)如此继续下去,直到两组变量之间的相关性被提取完毕为此。
9.2什么是典型变量?它具有哪些性质?答:在典型相关分析中,在一定条件下选取系列线性组合以反映两组变最之间的线性关系, 这被选出的线性组合配对被称为典型变量。
具体来说,炉=(呂D,Xf,絆)、X⑵=(皆,X化…,晋)U, = af 唧 + 甥材)+ •••+ 昭X)□評 X0)Y = 0⑴普)+专)*2) +...+€)疋)□ b⑴*2)在D(a(iy X(1)) = D(b(ir X(3)) = l的条件下,使得pS⑴‘X⑴,1)⑴‘X⑵)达到最大,则称$)乂1)、b⑴*2)是x(】)、X⑵的第一对典型相关变最。
典型变量性质:典型相关最化了两组变量之间的联系,反映了两组变最的相关程度。
1.D(U k) = l, D(\O = 1 (k = l,2,- -,r)Cov(Ui,UJ = 0, Cov(Y,\) = 0 (iHj)4 HO (i = j,i =l,2, ・.,r)2.Cov(U1,V J) = Jo (iHj)0 (j>09.3试分析一组变量的典型变量与其主成分的联系与区别。
第九章 典型相关分析9.1 什么是典型相关分析?简述其基本思想。
答: 典型相关分析是研究两组变量之间相关关系的一种多元统计方法。
用于揭示两组变量之间的内在联系。
典型相关分析的目的是识别并量化两组变量之间的联系。
将两组变量相关关系的分析转化为一组变量的线性组合与另一组变量线性组合之间的相关关系。
基本思想:(1)在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数。
即: 若设(1)(1)(1)(1)12(,,,)p X X X =X、(2)(2)(2)(2)12(,,,)q X X X =X 是两组相互关联的随机变量,分别在两组变量中选取若干有代表性的综合变量Ui 、Vi ,使是原变量的线性组合。
在(1)(1)(1)(2)()()1D D ''==a X b X 的条件下,使得(1)(1)(1)(2)(,)ρ''a X b X 达到最大。
(2)选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的一对。
(3)如此继续下去,直到两组变量之间的相关性被提取完毕为此。
9.2 什么是典型变量?它具有哪些性质?答:在典型相关分析中,在一定条件下选取系列线性组合以反映两组变量之间的线性关系,这被选出的线性组合配对被称为典型变量。
具体来说,()(1)()(1)()(1)()(1)1122i i i i i P PU a X a X a X '=+++a X()(2)()(2)()(2)()(2)1122i i i i i q qV b X b X b X '=+++b X在(1)(1)(1)(2)()()1D D ''==a X b X 的条件下,使得(1)(1)(1)(2)(,)ρ''a X b X 达到最大,则称(1)(1)'a X 、(1)(2)'b X 是(1)X 、(2)X 的第一对典型相关变量。
典型变量性质:典型相关量化了两组变量之间的联系,反映了两组变量的相关程度。
1. ()1,()1(1,2,,)k k D U D V k r ===(,)0,(,)0()i j i j Cov U U Cov V V i j ==≠2. 0(,1,2,,)(,)0()0()i i j i j i r Cov U V i j j r λ≠==⎧⎪=≠⎨⎪>⎩9.3 试分析一组变量的典型变量与其主成分的联系与区别。
答:一组变量的典型变量和其主成分都是经过线性变换计算矩阵特征值与特征向量得出的。
主成分分析只涉及一组变量的相互依赖关系而典型相关则扩展到两组变量之间的相互依赖关系之中,度量了这两组变量之间联系的强度。
()(1)()(1)()(1)()(1)1122i i i i i P P U a X a X a X '=+++a X ()(2)()(2)()(2)()(2)1122i i i i iq q V b X b X b X '=+++b X (1)(1)(1)(1)12(,,,)pX X X =X 、(2)(2)(2)(2)12(,,,)qX X X =X9.4 简述典型相关分析中载荷分析的内容及作用。
答:作用:进行典型载荷分析有助于更好解释分析已提取的p 对典型变量。
分析原始变量与典型变量之间相关性。
内容:令 (1)(2)*()p ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦a a A a (1)(2)*()p ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦b b B b 12p U U U ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦U 12p V V V ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦V *(1)*(2)==U A X V B X其中*A ,*B 为p 对典型变量系数向量组成的矩阵,U 和V 为p 对典型变量组成的向量。
则(1)*(1)(1)*11(,)(,)Cov Cov ==U X A X X A Σ(1)(1)(1)1/2(1)(,)(,)i ki kk k Corr U X Cov U X σ-===这里()1i D U =,1/2kk σ=。
记1/211V -为对角元素是1/2kk σ-的对角阵,所以有(1)(1)1/2(1)11,*(1)1/2(1)*1/2111111(,)(,)(,)U X Corr Cov Cov ---====R U X U V X A X V X A ΣV类似可得:(2)*1/22222,V X -=R B ΣV (2)*1/21222,U X -=R A ΣV (1)*1/22111,V X -=R B ΣV 对于经过标准化处理后得到的典型变量有:(1)*11,Z U Z =R A R ; (2)*22,Z V Z =R B R (2)*12,Z U Z =R A R ;(1)*21,Z V Z =R B R对于样本典型相关分析,上述结果中的数量关系同样成立。
9.5 简述典型相关分析中冗余分析的内容及作用。
答:典型冗余分析的作用即分析每组变量提取出的典型变量所能解释的该组样本总方差的比例,从而定量测度典型变量所包含的原始信息量。
第一组变量样本的总方差为11()tr p =R ,第二组变量样本的总方差为22()tr q =R 。
*ˆz A 和*ˆzB 是样本典型相关系数矩阵,典型系数向量是矩阵的行向量,*(1)ˆˆz =U A Z ,*(2)ˆˆz=VB Z 。
前r 对典型变量对样本总方差的贡献为(1)(1)(1)(2)(2)()()2ˆ,11ˆˆˆˆˆˆ()ik pr r r z zz zz zz U i k tr r =='''+++=∑∑aa a a aa (2)(1)(1)(2)(2)()()2ˆ,11ˆˆˆˆˆˆ()iKq rr r z z z zz z z Vi k tr r =='''+++=∑∑b b b b b b 则第一组样本方差由前r 个典型变量解释的比例为(1)(1)2ˆ,11ˆ|ik pr z U i k z U rd p===∑∑R第二组样本方差由前r 个典型变量解释的比例为(2)(2)2ˆ,11ˆ|ik qrz V i k z V rd q===∑∑R9.6 设X 和Y 分别是p 维和q 维随机向量,且存在二阶距,设p ≤q 。
它们的第i 对典型变量分别为()i a X '、()i b Y ',典型相关系数为i λ,(1,,)i p =。
令*X CX l =+,*Y DY m =+,其中C 、D 分别为,p p q q ⨯⨯阶非奇异阵,l 、m 分别为p 维、q 维随机向量,试证明⑴ **X Y 、的第i 对典型变量为1()*i C a X -'、1()*i D b Y -'。
⑵ 1()*i C a X -'与1()*i D b Y -'的典型相关系数为i λ。
9.7 对140名学生进行了阅读速度1x 、阅读能力2x 、运算速度1y 和运算能力2y 的四种测验,所得成绩的相关系数阵为10.030.240.590.0310.060.07R 0.240.0610.240.590.070.241⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦= 试对阅读本领与运算本领之间进行典型相关分析。
解:根据已知可得R ̂11=(10.030.031) R ̂12=(0.240.590.060.07)=R ̂′21 R ̂22=(10.240.241) R ̂−111=1(0.03−1−10.03)R̂−122=11−0.0576(0.03−1−10.03)M̂∗1z =R ̂−111R ̂12R ̂−122R ̂21= (0.50524550.072798410.08755550.01334270) M̂∗2z =R ̂−122R ̂21R ̂−111R ̂12=(0.10348010.24712470.17233400.4151081) 计算得M ̂∗1z ,M ̂∗2z 的特征值为λ12= 0.517878705 λ22=0.000709502提取第一典型变量为U 1∗=0.9852743Z 1(1)+0.1709812Z 2(1)V 1∗=−0.5121859Z 1(2)−0.8588746Z 2(2)其中Z i(1),Z j(2)分别为原始变量X i ,Y j 标准化后的结果。
按照常识,不应该有负数系数啊?不知道怎么回事。
9.8 某年级学生的期末考试中,有的课程闭卷考试,有的课程开卷考试。
44名学生的成试对闭卷(1X ,2X )和开卷(3X ,4X ,5X )两组变量进行典型相关分析。
9.9 邓讷姆(Dunham )在研究职业满意度与职业特性的相关程度时,对从一大型零售公司各分公司挑出的784位行政人员测量了5个职业特性变量:用户反馈、任务重要性、任务多样性、任务特性及自主性,7个职业满意度变量:主管满意度、事业前景满意度、财政满意度、工作强度满意度、公司地位满意度、工种满意度及总体满意度。
两组变量的样本相关矩阵为:111.000.49 1.00ˆ0.530.57 1.000.490.460.48 1.000.510.530.570.57 1.00R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦22 1.000.43 1.000.270.33 1.00ˆ0.240.260.25 1.000.340.540.460.28 1.000.370.320.290.300.35 1.000.400.580.450.270.590.31 1.00R ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦12210.330.320.200.190.300.370.210.300.210.160.080.270.350.20ˆˆ0.310.230.140.070.240.370.180.240.220.120.190.210.290.160.380.320.170.230.320.360.27R R ⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦试对职业满意度与职业特性进行典型相关分析。
9.10 试对一实际问题进行典型相关分析。