质数与合数(含答案)
- 格式:doc
- 大小:726.00 KB
- 文档页数:8


第3讲质数与合数阿拉伯数字无疑是人类历史上最伟大的发明之一,其本身蕴含的规律更是数学学科中最璀璨的明珠!质数和合数的分类产生了哥德巴赫对于自然数a 和b (0b ≠),若a b ÷没有余数,则a 是b 的倍数,b 是a 的约数。
特殊地,0是任意非零自然数的倍数。
质数:除了1和本身,没有其他约数的自然数叫质数。
合数:除了1和本身,还有其他约数的自然数叫合数。
特殊地,1既不是质数也不是合数。
最小的合数是4,最小的质数是2,且2是唯一的偶质数。
质因数:如果一个质数是某个数的约数,那么就编写说明知识要点【例1】对7个不同质数求和,和为58,则最大的质数是多少【分析】七个质数若全部是奇数,则和一定是奇数,而58是偶数,则七个质数中必定含有唯一的偶质数2,所以最小的质数是2,从2开始,最小的七个连续质数是2,3,5,7,11,13,17,和为58,所以题中的七个质数只能是从2开始的七个连续质数,最大为17。
【温馨提示】2是唯一的偶质数,是偶数中的“叛徒”,所以质数也经常与奇偶性相结合,主要考察“2”.【拓展】已知a、b、c、d都是质数,且130959179a b c d+=+=+=+,求a、b、c、d的值。
【分析】959179+=+=+,所以b、c、d应该都是奇数,所以a是唯一的偶质数2,依此可求得:b c db=,41d=.c=,53a=,372【例2】从小到大写出5个质数,使后面数都比前面的数大12。
这样的数有几组【分析】考虑到质数中除了2以外其余都是奇数,因此这5个质数中不可能有2;又质数中除了2和5,其余质数的个位数字只能是1、3、7、9。
若这5个质数中最小的数其个位数字为1,则比它大24的数个位即为5,不可能是质数;若最小的数其个位数字为3,则比它大12的数个位即为5,也不可能为质数;由此可知最小的数其个位数字也不可能是7和9,因此最小的数只能是5,这5个数依次是5,17,29,41,53。


第三讲 质数与合数什么是质数?每一个数都能写成若干个数相乘的形式,考虑到任何一个数都能写成若干个1乘以它本身的形式,所以不考虑1作为乘数的情况:623=⨯,824222=⨯=⨯⨯,122634223=⨯=⨯=⨯⨯……这些数都能拆成若干个不为1的数相乘的形式,我们把这样的数称为合数.而像2,3,7……这些不能拆成若干个不为1的数相乘形式的数,我们称之为质数.如果说得形象一点,质数就是“拆不开”的数,合数就是拆得开的数.严格说来,质数就是只能被1和自身整除的数;合数是除了1和它本身之外,还能被其它数整除的数.注意,1既不是质数也不是合数.我们先来看一个关于质数的小问题,提高大家对质数的熟悉程度:请写出所有颠倒个位十位之后还是质数的两位质数._____________________________________________(填写在横线上)相信对100以内的质数比较熟悉的同学,做这个题目会很轻松.质数是我们后面学习的基础,因此同学们一定要牢牢记住常见的质数.请同学们在下面的横线上写出100以内的所有质数:同学们还可以这样做:从大到小....写出100以内的质数.如果你能一个不少地写出来,说明你对100以内的质数确实掌握得很牢固了^_^.当然,同学们写出的这些质数只是质数大军中的冰山一角.在100以上还有无穷多个质数,比如接着100的就有四个质数:101,103,107,109.【分析】1~56以内的质数有哪些?把它们列出来,然后依次找出对应的汉字,这句话就出来了.下面是主试委员会为第六届“华杯赛”写的一首诗:美少年华朋会友,幼长相亲同切磋; 杯赛联谊欢声响,念一笑慰来者多; 九天九霄志凌云,九七共庆手相握; 聚起华夏中兴力,同唱移山壮丽歌.将诗中56个字第1行左边第一字起逐行逐字编为1—56号,再将号码中的质数由小到大找出来,将它们对应的字依次排成一行,组成一句话,请写出这句话.自然数N 是一个两位数,它是一个质数,而且N 的个位数字与十位数字都是质数,这样的自然数有多少个?【分析】对于第1问,依次枚举即可,可知这两个不同的质数一定都是奇数.那么后两问中的质数可以都是奇数吗?如果三个互不相同的质数相加,和为52,这三个质数可能是多少?通过前面的学习,我们对质数已经有了基本了解.下面我们来学习这一讲中最重要的内容:分解质因数.分解质因数是指把一个数写成质因数相乘的形式.如:30235=⨯⨯,1002255=⨯⨯⨯,28022257=⨯⨯⨯⨯.同学们请注意:分解式应该把质因数按从小到大的顺序写好,每个数分解质因数的形式是唯一的.分解质因数的方法一般是短除法,如下图所示,我们将30分解质因数,在计算的过程(1)如果两个不同的质数相加等于26,那么这两个质数的乘积可能是多少?请全部写出. (2)如果两个不同的质数相加等于25,那么这两个质数的乘积可能是多少?请全部写出. (3)三个互不相同的质数相加,和为40,这三个质数的乘积可能是多少?请全部写出.中要善用各种特殊数的整除特性.100在分解质因数时也可以写成:2210025=⨯;280在分解质因数时也可以写成3280257=⨯⨯.这种写法更简洁更方便,其中位于质因数右上角,表示质因数个数的数叫作指数,如:这里280的分解式中5和7的指数都是1,写的时候可以省略.如何确定一个大数是不是质数呢?我们要判断197是不是质数,难道需要一一验算197以内的所有质数吗?同学们不用担心,数学家们早就为我们准备了简单的方法,只需要试很少的几个就能判断.例如我们要判断197是否为质数,只需要验算15以内的质数就足够了!因为1515225⨯=比197大.类似的,如果我们要判断2011是不是质数,只需要验算45以内的质数,因为45452025⨯=比2011大.有了这个方法,同学们以后判断一个大数是不是质数就非常方便了.「分析」将一个数分解质因数,可以从最小的质数开始,一个一个去试商,写成短除的形式.请把下面的数分解质因数: (1)373;(2)12660.请把下面的数分解质因数:(1)360;(2)539;(3)999;(4)10101.2210025=⨯指数3280257=⨯⨯ 指数2 30 315 5能整除30相除后得在整数问题中,有一类特殊的问题,专求乘积末尾连续0的个数.解决这类问题的方法同样是质因数分解.下面我们来看一个例题.【分析】乘积的末尾要出现一个0,只需要乘数中凑出一个10,那么能凑出来几个10,末尾就有多少个连续的0.注意到1025=⨯,我们只需要计算这个算式中含有的质因数2和5的个数就可以了.算式12330⨯⨯⨯⨯的计算结果的末尾有多少个连续的0?分解质因数是学习数论问题时非常重要的方法,大家一定要能熟练的将一个数分解质因数,这应该作为一项基本的能力来培养.下面我们来看看如何利用分解质因数来解决实际的问题.三个连续自然数的乘积等于39270,那么这三个数的和等于多少?算式123100⨯⨯⨯⨯计算结果的末尾有多少个连续的0?「分析」39270是三个自然数的乘积,于是先将39270分解质因数,再对这些质因数进行适当的组合,凑出题目中的三个连续自然数.由于连续自然数相互之间比较接近,所以凑的时候也必须尽量接近.360与一个三位数的乘积是完全平方数,这个三位数最小是多少?【分析】完全平方数是两个相同数的乘积,那么分解后它的每个质因数的次数都是偶数.而32360235=⨯⨯,它不是一个平方数.它最小再乘上多少,结果就是平方数了?通过上面例题的讲解,相信大家能体会到分解质因数的好处.它就像手术刀一样,把整数解剖开来,让我们把整数的组成结构看得一清二楚.很多看似复杂的问题,如果从分解质因数的角度来看,就会变得非常简单.课堂内外质数有无穷个吗?在正整数里走得越远,我们就发现质数变得越来越稀少.有人可能会问:质数出现频率越来越小,它们会不会在某处终止呢?会不会从某个数开始之后就没有质数了呢?早在公元前300年左右,欧几里得就第一次证明了质数有无穷多个.他用的是如下的反证法:设n代表最后一个质数,那么从2到n的所有质数的积是2357n⨯⨯⨯⨯⨯.将这个积加1称为k,因为2,3,5,7,11,…,n都不能整除k,所以k必然含有一个更大的质因数!这与n代表最后一个质数相矛盾!作业1.(1)如果两个不同的质数相加等于39,那么这两个质数的乘积是多少?(2)三个互不相同的质数相加,和为30,这三个质数的乘积是多少?2.自然数49,87,101,103,121中,哪些是质数?3.请把下面的数分解质因数:(1)240;(2)1080.4.三个连续自然数的乘积为336,则这三个数的和是多少?⨯⨯⨯⨯的计算结果的末尾有多少个连续的0?5.算式12335第三讲质数与合数例题1.答案:少年朋友亲切联欢一九九七相聚中山详解:1~56中的质数有2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53共16个.例题2.答案:(1)69、133;(2)46;(3)434详解:(1)26可以拆成3与23的和,或者7与19的和;(2)25只能拆成2和23的和;(3)三个数的和是偶数,可以是三个偶数,或者一偶两奇.考虑到质数中只有2是偶数,可知一定是一偶两奇,且偶数是2.另外两个奇数是7和31.例题3.答案:(1)32360235=⨯;=⨯;(3)3999337=⨯⨯;(2)2539711(4)10101371337=⨯⨯⨯.例题4.答案:24详解:末尾0的个数与算式结果所含质因数2和5的个数有关,结果中质因数的个数又与乘数中质因数的个数有关.因为2的个数要比5的个数多,所以0的个数等于5的个数.乘数中5的倍数有20个,25的倍数有4个,所以质因数5的个数有20424+=个.末尾有24个连续的0.例题5.答案:102详解:3927023571117=⨯⨯⨯⨯⨯.考虑其中最大的质因数17,三个自然数中一定有17的倍数.如果是17,那么一定有16或18.这不可能.如果是34,另外两个数是33和35,正好满足.333435102++=.例题6.答案:160详解:完全平方数的每个质因数的次数一定是偶数.而32=⨯⨯,360235至少要再乘上2510⨯=才是一个平方数.题目要求是三位数,即是一个平方数.可知空格上也要填入一个平方数,最⨯⨯36010____三位数小要填16.要乘的三位数最小是160.练习1. 答案:23、37、53、73简答:一位数中的质数只有2、3、5、7.而N 的个位数字只能是3和7,分类枚举即可. 练习2. 答案:2、3、47或者2、7、43或者2、13、37或者2、19、31简答:三个质数一定是一偶两奇,偶数是2. 练习3. 答案:(1)质数;(2)212660235211=⨯⨯⨯. 练习4. 答案:7简答:1~30中5的倍数有6个,25的倍数有1个,所以其中有7个5.计算结果的末尾有7个连续的0.作业1. 答案:(1)74;(2)230或374简答:(1)39237=+,乘积为74.(2)30252321117=++=++,乘积为230或374.作业2. 答案:101,103.作业3. 答案:(1);(2).作业4. 答案:21简答:,和为21. 作业5. 答案:8个简答:看含有因子5的个数,是5的倍数的数有7个,是25的倍数的数有1个,共8个.4336237678=⨯⨯=⨯⨯ 331080235=⨯⨯ 4240235=⨯⨯。

合数和质数的练习册及答案### 合数和质数的练习册及答案#### 练习题一:判断质数1. 判断下列数字是否为质数:- 2- 3- 4- 5- 9- 13- 16- 17- 23#### 练习题二:找出合数2. 找出100以内的所有合数。
#### 练习题三:质数序列3. 列出100以内的质数序列。
#### 练习题四:合数分解4. 将下列合数分解为质因数:- 12- 18- 24- 36#### 练习题五:质数与合数的个数5. 计算100以内质数和合数的个数。
#### 练习题六:质数的应用6. 解释质数在密码学中的应用。
#### 答案解析#### 练习题一:判断质数1. 质数是指只能被1和自身整除的大于1的自然数。
- 2(质数)- 3(质数)- 4(合数)- 5(质数)- 9(合数)- 13(质数)- 16(合数)- 17(质数)- 23(质数)#### 练习题二:找出合数2. 100以内的合数有:- 4, 6, 8, 9, 10, ..., 98, 99#### 练习题三:质数序列3. 100以内的质数序列:- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ..., 97 #### 练习题四:合数分解4. 合数分解为质因数:- 12 = 2 × 2 × 3- 18 = 2 × 3 × 3- 24 = 2 × 2 × 2 × 3- 36 = 2 × 2 × 3 × 3#### 练习题五:质数与合数的个数5. 100以内质数有25个,合数有74个。
#### 练习题六:质数的应用6. 质数在密码学中的应用主要是基于其难以因式分解的特性。
例如,在RSA加密算法中,公钥和私钥的生成依赖于两个大质数的乘积。
通过这些练习题,学生可以加深对质数和合数概念的理解,并学会如何应用这些数学概念解决实际问题。

质数合数单元测试题目及答案一、选择题(每题2分,共20分)1. 下列哪个数是质数?A. 4B. 9C. 15D. 172. 100以内最大的质数是什么?A. 97B. 99C. 100D. 1013. 一个数如果只有1和它本身两个因数,那么这个数是什么?A. 合数B. 质数C. 偶数D. 奇数4. 以下哪个数是合数?A. 2B. 3C. 5D. 45. 质数的定义是什么?A. 只有1和它本身两个因数的数B. 能被2整除的数C. 能被3整除的数D. 能被4整除的数6. 一个数的因数除了1和它本身外,还有其他因数,那么这个数是什么?A. 质数B. 合数C. 偶数D. 奇数7. 以下哪个数不是质数?A. 29B. 31C. 33D. 378. 一个数的因数个数是奇数个,那么这个数是什么?A. 质数B. 合数C. 偶数D. 奇数9. 质数和合数的区别是什么?A. 质数是偶数,合数是奇数B. 质数只有两个因数,合数有多个因数C. 质数是奇数,合数是偶数D. 质数和合数都是偶数10. 以下哪个数是最小的合数?A. 0B. 1C. 2D. 4二、填空题(每题2分,共20分)11. 质数是指只有________和它本身两个因数的自然数。
12. 合数是指除了1和它本身外,还有________的自然数。
13. 100以内的质数有________、________、________等。
14. 一个数的因数个数是偶数个,那么这个数至少是________。
15. 2是唯一的________,因为它是唯一的偶数质数。
16. 质数和合数都是________的子集。
17. 一个数如果只有1和它本身两个因数,那么它一定是________。
18. 一个数如果除了1和它本身外,还有其他因数,那么它一定是________。
19. 质数和合数的区别在于它们的因数个数,质数有________个因数,合数有________个因数。
20. 100以内最大的质数是________。
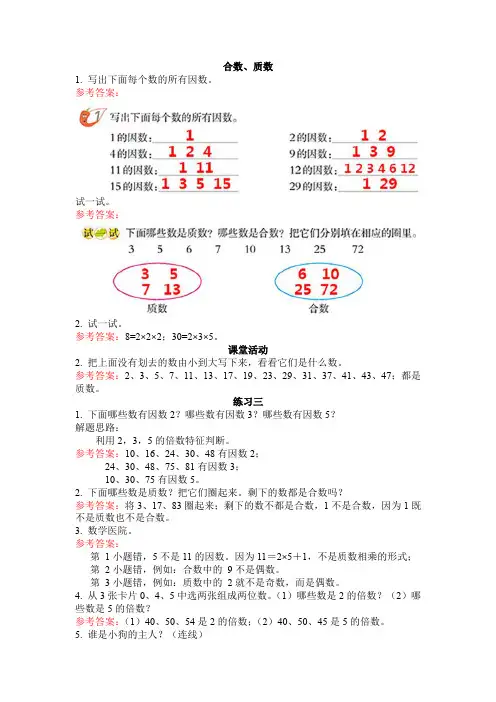
合数、质数1. 写出下面每个数的所有因数。
参考答案:试一试。
参考答案:2. 试一试。
参考答案:8=2×2×2;30=2×3×5。
课堂活动2. 把上面没有划去的数由小到大写下来,看看它们是什么数。
参考答案:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47;都是质数。
练习三1. 下面哪些数有因数2?哪些数有因数3?哪些数有因数5?解题思路:利用2,3,5的倍数特征判断。
参考答案:10、16、24、30、48有因数2;24、30、48、75、81有因数3;10、30、75有因数5。
2. 下面哪些数是质数?把它们圈起来。
剩下的数都是合数吗?参考答案:将3、17、83圈起来;剩下的数不都是合数,1不是合数,因为1既不是质数也不是合数。
3. 数学医院。
参考答案:第1小题错,5不是11的因数。
因为11=2×5+1,不是质数相乘的形式;第2小题错,例如:合数中的9不是偶数。
第3小题错,例如:质数中的2就不是奇数,而是偶数。
4. 从3张卡片0、4、5中选两张组成两位数。
(1)哪些数是2的倍数?(2)哪些数是5的倍数?参考答案:(1)40、50、54是2的倍数;(2)40、50、45是5的倍数。
5. 谁是小狗的主人?(连线)解题思路:先把每个人身上数分解质因数,再连线。
参考答案:6. 把下列各数写成质数相乘的形式。
参考答案:40=2×2×2×5;52=2×2×13;90=2×3×3×5;96=2×2×2×2×2×3。
7. 填表。
解题思路:把这2个数分解质因数,注意1和这个数本身也是这个数的因数。
参考答案:观察发现:除了1和这个数本身外,这个数的其它因数的乘积等于这个数。
8. 在1~100的自然数中,找出既是3的倍数也是5的倍数的所有偶数和所有奇数,说说你是怎么找的?解题思路:既是3的倍数也是5的倍数,一定也是15的倍数,先找出在100以内是15的倍数的两位数;再筛选奇偶数。


《质数与合数(一)》配套练习题
一、解答题
1、有两个质数,它们的和与差也都是质数,那么这两个质数分别是多少?
2、在一个两位质数两个数字交换位置后还是一个两位质数,所有这种质数
的和是多少?
3、从小到大写出5个质数,使后面的数都比前面的数大12.
4、用1、2、3、4、
5、
6、
7、
8、9这9个数字组成若干质数,要求每个数字都要用到并且只用一次,那么最多能组成多少个质数?最多的组成方式
共有多少种?
5、用0~9各一个组成4个一位质数与两个三位质数,这六个质数之和最
大是多少?
6、三个质数a,b,c,满足a+bc=2007,那么a+b+c的最大值是多少?
1。

五年级数学下册《质数和合数》练习题及答案解析学校:___________姓名:___________班级:________________一、判断题1.任何质数加上1都能成为合数。
( )2.把一根16cm长的铁丝围成一个长是a厘米,宽是b厘米的长方形,若a和b都是质数,则长方形的面积是215cm。
( )3.在全部自然数里,不是质数就是偶数。
( )4.所有的质数一定是奇数,所有的合数都是偶数。
( )5.最小的质数是1,最小的合数是4。
( )二、填空题6.一个两位数,个位上是最小的合数,十位上是3的倍数,这个数最大是( )。
7.6的倍数中,最小倍数是( ),100以内3的最大倍数是( );28的因数中最大的一位数是( );20以内最大的质数是( )。
8.20以内所有质数是( ),其中最大的质数比最小的质数多( )。
9.176是一个( )分数,它的分数单位是( ),它有( )个这样的分数单位,再添上( )个这样的分数单位就是最小的合数。
10.下面的游戏规则公平吗?在后面的括号里填“公平”或“不公平”。
(1)淘气和弟弟玩五子棋,他们设计了一个摸牌方案决定谁先走。
将下面4张扑克牌背面朝上,任意摸一张牌,摸到质数弟弟先走,摸到合数淘气先走。
( )(2)足球比赛中,裁判用抛硬币的方法决定谁先开球。
( )(3)同学们玩跳皮筋,常用“石头、剪刀、布”的方法来决定谁先跳。
( )(4)下象棋时,先掷骰子,朝上的数字比3大,红方先走;比3小,黑方先走。
( )11.( )既不是质数也不是合数,( )是偶数但不是合数。
三、解答题12.三个不同的质数之和是50,写出这三个质数。
13.用数字1,2,3,组成一位数、两位数和三位数,其中哪些是质数,哪些是合数?四、选择题14.两个不同质数的积—定是()。
A.合数B.质数C.奇数D.偶数15.下面()组的两个数互质.A.15和16B.14和21C.39和1316.要使3□15能被3整除,□里最小能填()。

24.质数、合数与因数分解知识纵横一个大于1的正整数,若除了1与它自身,再没有其他的约数,•这样的正整数叫做质数;一个大于1的正整数,除了1与它自身,若还有其他的约数,这样的正整数称为合数,这样,我们可以按约数个数将正整数分为三类:正整数1⎧⎪⎨⎪⎩单位质数合数质数、合数有下面常用的性质:1.1不是质数,也不是合数;2是惟一的偶质数.2.若质数p│ab,则必有p│a或p│b.3.若正整a,b的积是质数p,则必有a=p或b=p.4.算术基本定理:任意一个大于1的整数N能分解成k个质因数的乘积,•若不考虑质因数之间的顺序,则这种分解是惟一的,从而N可以写成标准分解形式:N=p1a1·p2a2·…p k ak其中p1<p2<…<p k,p i为质数,a i为非负整数.(i=1,2,…k).例题求解【例1】已知三个不同的质数a,b,c满足ab b c+a=2000,那么a+b+c=_____.(第15届江苏省竞赛题) 思路点拨运用乘法分配律、算术基本定理,从因数分解入手,突破a的值.解:42 提示:由a(b b c+1)=24×53.【例2】不超过100的所有质数的乘积减去不超过60且个位数字为7•的所有质数的乘积所得之差的个位数字是( ).A.3B.1C.7D.9思路点拨从寻找适合题意的质数入手.解:选D 提示2与5的积为10,不超过60且个位数字为7的所有质数共4个,它们是7,17,37,47,10-1=9。
【例3】求这样的质数,当它加上10和14时,仍为质数. (上海市竞赛题)思路点拨由于质数的分布不规划,不妨从最小的质数进行实验,但这样的质数惟一吗?还需按剩余类的方法进行讨论.解:3符合要求提示:当p=3k+1时,p+10=3k+11,P+14=3(k+5),显然p+14是合数;当p=3k+2时,p+10=3(k+4)是合数,当p=3k时,只有k=1才符合题意。
第3讲质数与合数阿拉伯数字无疑是人类历史上最伟大的发明之一,其本身蕴含的规律更是数学学科中最璀璨的明珠!质数和合数的分类产生了哥德巴赫猜想等世界著名的命题,学习质数和合数,窥探数字的奥秘!对于自然数a 和b (0b ≠),若a b ÷没有余数,则a 是b 的倍数,b 是a 的约数。
特殊地,0是任意非零自然数的倍数。
质数:除了1和本身,没有其他约数的自然数叫质数。
合数:除了1和本身,还有其他约数的自然数叫合数。
特殊地,1既不是质数也不是合数。
最小的合数是4,最小的质数是2,且2是唯一的偶质数。
质因数:如果一个质数是某个数的约数,那么就说这个质数是这个数的质因数。
互质数:公约数只有1的两个自然数,叫做互质数。
分解质因数:把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
编写说明知识要点【例1】 对7个不同质数求和,和为58,则最大的质数是多少?【分析】 七个质数若全部是奇数,则和一定是奇数,而58是偶数,则七个质数中必定含有唯一的偶质数2,所以最小的质数是2,从2开始,最小的七个连续质数是2,3,5,7,11,13,17,和为58,所以题中的七个质数只能是从2开始的七个连续质数,最大为17。
【温馨提示】2是唯一的偶质数,是偶数中的“叛徒”,所以质数也经常与奇偶性相结合,主要考察“2”.【拓展】 已知a 、b 、c 、d 都是质数,且130959179a b c d +=+=+=+,求a 、b 、c 、d 的值。
【分析】959179b c d +=+=+,所以b 、c 、d 应该都是奇数,所以a 是唯一的偶质数2,依此可求得:2a =,37b =,41c =,53d =.【例2】 从小到大写出5个质数,使后面数都比前面的数大12。
这样的数有几组?【分析】 考虑到质数中除了2以外其余都是奇数,因此这5个质数中不可能有2;又质数中除了2和5,其余质数的个位数字只能是1、3、7、9。
若这5个质数中最小的数其个位数字为1,则比它大24的数个位即为5,不可能是质数;若最小的数其个位数字为3,则比它大12的数个位即为5,也不可能为质数;由此可知最小的数其个位数字也不可能是7和9,因此最小的数只能是5,这5个数依次是5,17,29,41,53。
第二讲质数、合数和分解质因数一、基本概念和知识1.质数与合数一个数除了1和它本身,不再有别的约数,这个数叫做质数(也叫做素数)。
一个数除了1和它本身,还有别的约数,这个数叫做合数。
要特别记住:1不是质数,也不是合数。
2.质因数与分解质因数如果一个质数是某个数的约数,那么就说这个质数是这个数的质因数。
把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
例:把30分解质因数。
解:30=2×3×5。
其中2、3、5叫做30的质因数。
又如12=2×2×3=22×3,2、3都叫做12的质因数。
二、例题例1 三个连续自然数的乘积是210,求这三个数.解:∵210=2×3×5×7∴可知这三个数是5、6和7。
例2 两个质数的和是40,求这两个质数的乘积的最大值是多少?解:把40表示为两个质数的和,共有三种形式:40=17+23=11+29=3+37。
∵17×23=391>11×29=319>3×37=111。
∴所求的最大值是391。
答:这两个质数的最大乘积是391。
例3 自然数123456789是质数,还是合数?为什么?解:123456789是合数。
因为它除了有约数1和它本身外,至少还有约数3,所以它是一个合数。
例4 连续九个自然数中至多有几个质数?为什么?解:如果这连续的九个自然数在1与20之间,那么显然其中最多有4个质数(如:1~9中有4个质数2、3、5、7)。
如果这连续的九个自然中最小的不小于3,那么其中的偶数显然为合数,而其中奇数的个数最多有5个.这5个奇数中必只有一个个位数是5,因而5是这个奇数的一个因数,即这个奇数是合数.这样,至多另4个奇数都是质数。
综上所述,连续九个自然数中至多有4个质数。
例5 把5、6、7、14、15这五个数分成两组,使每组数的乘积相等。
解:∵5=5,7=7,6=2×3,14=2×7,15=3×5,这些数中质因数2、3、5、7各共有2个,所以如把14(=2×7)放在第一组,那么7和6(=2×3)只能放在第二组,继而15(=3×5)只能放在第一组,则5必须放在第二组。
合数与质数答案典题探究例1.在横线内填上合适的质数.26=23+312=7+5=13+13=7+19=3+23=2×13.考点:合数与质数.专题:数的整除.分析:在自然数中,除了1和它本身外,没有别的因数的数为质数,据此填空即可.解答:解:26=23+3 12=7+5=13+13=7+19=3+23=2×13故答案为:23,3,13,13,7,19,3,23,2,13,7,5.点评:明确质数的意义,是解答此题的关键.例2.寻找符合条件的数:小于100,并且由3个不同质数相乘得到.考点:合数与质数.专题:数的整除.分析:只要把这个小于100的数,分解质因数即可得出.解答:解:2×3×7=42点评:此题考查了一个数分解质因数的方法.例3.自然数N是一个两位数,它是一个质数,而且N的个位数字与十位数字都是质数,这样的自然数有多少个?考点:合数与质数.专题:数的整除.分析:根据个位数字与十位数字都是质数,可得这个两位质数的个位数字和十位数字只能是:2、3、5、7.解答:4解:因为N是质数,且其个位数字和十位数字都是质数,那么十位数字和个位数字只能是:2、3、5、7,所以符合题意的两位数质数有:23,37,53,73,有4个;答:这样的自然数有4个.点评:此题考查了质数的灵活应用,理解十位数字与个位数字都是质数的两位质数是由:2、3、5、7组成的是本题的关键.例4.一个式子有8个空“空格”,在这些“空格”里,填进20以内各不相同的质数,使A是整数,并且尽可能大.A=(2+3+5+11+13+17+19)÷7.考点:合数与质数;整数的除法及应用.分析:根据质数的意义可知,20以内的质数有2、3、5、7、11、13、17、19;它们的和为2+3+5+7+11+13+17+19=77,则算式中除数应用为77的约数,能被77整除的只有7和11,因此A最大为(77﹣7)÷7=10.解答:解:20以内的质数的质数的和为:2+3+5+7+11+13+17+19=77,77=7×11,所以要使A最大,则A=[2+3+5+11+13+17+19]÷7=70÷7=10,即A能取得的最大整数是10.故答案为:2,3,5,11,13,17,19,7.点评:首先根据质数的意义确定20以内的质数并求出它们的和是完成本题的关键.演练方阵A档(巩固专练)一.选择题(共10小题)1.(•龙湖区)2、3、5、7都是()A.奇数B.偶数C.质数考点:合数与质数.分析:自然数中,能被2整除的数为偶数,不能被2整除的数为奇数;自然数中,除了1和它本身外,没有别的因数的数为质数.根据以上定义对题目中的数字进行分析即能得出正确选项.解答:解:根据偶数、奇数及质数的定义可知:在2、3、5、7这四个数字中,2为偶数,3,5,7为奇数,2、3、5、7全是质数.故选:C.点评:通过本题可以看出,2既为质数,同时也是偶数.2.(•新余模拟)一个两位数,个位和十位上的数字都是合数,并且互质,这个两位数最小是()A.89 B.28 C.49考点:合数与质数.专题:整数的认识.分析:自然数中,除了1和它本身外,还有别的因数的数为合数.由此可知,小于10的合数有4,6,8,9.即这个两位数由有4,6,8,9中的两个合数组成.又这两个数互质,只有公因数1的两个数为互质数,而这4个数中,9与4,8互质,所以这个两位数最小是49..解答:解:根据合数的意义可知,这个两位数由有4,6,8,9中的两个合数组成,而这4个数中,9与4,8互质,所以这个两位数最小是49.故选:C.点评:首先根据合数的定义确定组成这个两位数的数的取值范围,然后根据互质数的意义确定是完成本题的关键.3.(•石阡县模拟)一个合数至少有()个因数.A.3个B.3个以上C.3个或3个以上考点:合数与质数.专题:数的整除.分析:合数是指一个大于1的自然数,除了1和它本身两个因数外,还有其它的因数,说明一个合数有3个或3个以上的因数.据此做出选择即可.解答:解:一个合数有3个或3个以上的因数.故选:C.点评:此题考查合数的意义,关键是看这个数有几个因数,有3个或3个以上的因数的数一定是合数.4.(•北海)下面()组中的两个数是合数,又是互质数.A.7和8 B.10和12 C.15和16考点:合数与质数.专题:数的整除.分析:合数是含有1和它本身两个因数外还含有其它因数的数,互质数是只有公因数1的两个数,据此依次分析选择.解答:解:A、7和8是互质数,但7是质数,不是合数,所以不合题意;B、10和12都是合数,但是10和12不是互质数,所以不合题意;C、15和16都是合数,15和16又是互质数,所以符合题意;故选:C.点评:本题主要考查互质数、合数的意义.5.(•汉阳区)一个数如果只有2个因数,那么这个数一定是()A.偶数B.奇数C.质数D.合数考点:合数与质数.专题:整数的认识.分析:在自然数中,除了1和它本身外,没有别的因数的数为质数.即质数只有两个因数,即1和它本身.解答:解:根据质数的意义可知,一个数如果只有2个因数,那么这个数一定是质数.故选:C.点评:自然数中,质数只有两个因数,1只有一个因数,零有没因数,合数最少有三个因数.6.(•蕲春县模拟)是一个最简分数,a和c一定是()A.质数B.合数C.互质数D.不一定考点:合数与质数.分析:首先弄清什么样的分数是最简分数,据此解答.解答:解:分数的分子和分母只有公约数1的分数叫做最简分数,由此得一个最简分数的分子和分母一定是互质数.故选C.点评:此题主要考查最简分数的意义及互质数的概念.7.(•黄岩区)一个比l大的数除了1和它本身之外,没有其他的因数,这个数是()A.质数B.合数C.奇数D.偶数考点:合数与质数.专题:数的整除.分析:根据质数和合数的含义:除了1和它本身以外,不含其它因数的数是质数;除了1和它本身外,还含有其它因数的数是合数;据此解答即可.解答:解:由质数的含义可知:一个比l大的数除了1和它本身之外,没有其他的因数,这个数是质数;故选:A.点评:明确质数的含义,是解答此题的关键.8.(•渝北区)下面的数是质数的是()A.1B.2C.4考点:合数与质数.专题:综合判断题.分析:自然数中,除了1和它本身外没有别的因数的数为质数,除了1和它本身外还有别的因数的数为合数.据此对各选项中的数字进行分析即能得出正确选项.解答:解:A、1不是质数也不是合数;B、2是质数;C、4是合数;故选:B.点评:自然数中,质数与合数是根据因数的多少进行定义的.9.(•安岳县模拟)下列叙述正确的是()A.互质的两个数没有公因数B.两个分数大小相等,分数单位也一定相等C.小兰完成的作业量一定,她已完成的作业和未完成的作业量成反比例D.两个面积相等的三角形,不一定能拼成一个平行四边形考点:合数与质数;分数的意义、读写及分类;辨识成正比例的量与成反比例的量;三角形的特性.专题:综合判断题.分析:A,根据互质数的意义,公因数只有1的两个数叫做互质数.所以互质的两个数没有公因数.此说法错误.B,两个分数的大小相等,分数单位不一定相同,如:和相等,但是它们的分数单位不同.所以两个分数相等,分数单位也一定相同.此说法错误.C,根据反比列的意义,两种相关联的量,如果它们对应的两个数的积一定,这两种相关联的量成反比列.所以,小兰完成的作业量一定,她已完成的作业和未完成的作业量成反比例.此说法错误.D,因为只有两个完全一样的三角形,才能拼成一个平行四边形,两个三角形的面积相等,不一定完全一样,所以,两个面积相等的三角形,不一定能拼成一个平行四边形.此说法正确.解答:解:根据上面的分析知:说法正确的是:两个面积相等的三角形,不一定能拼成一个平行四边形.故选:D.点评:此题考查的目的是理解互质数的意义、分数单位的意义、反比列的意义,明确:只有两个完全一样的三角形,才能拼成一个平行四边形.10.(•华亭县模拟)正方形的边长是质数,它的周长一定是(),它的面积一定是()A.质数B.合数C.既不是质数也不是合数考点:合数与质数;正方形的周长;长方形、正方形的面积.分析:正方形的边长是质数,设这个质数是a,则它的周是4a,它的面积是a2,然后根据约数个数分析,是质数还是合数,据此解答.解答:解:正方形的边长是质数,设这个质数是a,则它的周是4a,4a含有1、2、4、a、2a、4a,含有6个约数,它的面积是a2,a2含有:1、a、a2共计3个约数,即4a和a2含有至少3个约数,所以都是合数;故选:B.点评:本题主要考查质数合数的意义,注意本题设这个质数是a,则它的周长是4a,它的面积是a2,然后根据约数个数分析.二.填空题(共10小题)11.(•台州)的分数单位是,再添上14个这样的分数单位是最小的素数.考点:合数与质数.分析:根据分数的意义和最小的素数(质数)是2来进行分析,然后填出即可.解答:解:的分数单位是.因为:+=2;所以:再添上14个这样的分数单位是最小的素数.故答案为:,14.点评:此题考查分数的认识与质数合数.12.(•浙江)在6、10、18、51这四个数中,51既是合数又是奇数.10和51互质.考点:合数与质数;奇数与偶数的初步认识.分析:合数的含义:在自然数中除了1和它本身外还有其它因数的数;奇数的含义:在自然数中不能被2整除的数叫作奇数;在自然数中,如果两个数的公因数只有1,那么这两个数称为互质数.解答:解:在6、10、18、51这四个数中,合数有:6,10,18,51;奇数有:51;互质的数是:10与51;所以在6、10、18、51这四个数中,51即是合数又是奇数,10与51互质.故答案为:51,10,51.点评:此题主要考查的是合数、奇数和互质数的知识.13.(•万州区)一个质数和比它小的每一个非零自然数都互质.正确.考点:合数与质数.分析:自然数中,除了1和它本身外,没有别的因数的数为质数;假如这个质数与比它小的某个非零自然数不互质,那么这个质数与这个非零自然数就有“除1和其本身之外的”公约数,这个结论和质数的定义相矛盾,即“一个素数肯定与比它小的任意非零自然数互质.”解答:解:根据质数的定义可知,一个质数和比它小的每一个非零自然数都互质的说法是正确的.故答案为:正确.点评:一个质数和比它大的非零自然数中只与它的倍数不互质,除了其倍数外,与其它自然数都互质.14.(•福田区模拟)如果a和b是大于0的相邻的自然数,那么a和b一定是互质数.√.(判断对错)考点:合数与质数.专题:数的整除.分析:在自然数中,只有公因数1的两个数为互质数.根据自然数的排列规律及公因数的意义可知,任何一对大于0的相邻的两个自然数只有公因数1,所以如果a和b是大于0的相邻的自然数,那么a和b一定是互质数.解答:解:根据互质数的意义可知,如果a和b是大于0的相邻的自然数,那么a和b一定是互质数是正确的.故答案为:√.点评:明确任何一对大于0的相邻的两个自然数只有公因数1是完成本题的关键.15.(•芜湖县)有公约数1的两个数叫做互质数.×.(判断对错)考点:合数与质数.专题:数的整除.分析:根据互质数的意义,公因数只有1的两个数叫做互质数.1是任何两个非0自然数的公因数.解答:解:公因数只有1的两个数叫做互质数.1是任何两个非0自然数的公因数.所以有公约数1的两个数叫做互质数.出说法错误.故答案为:×.点评:此题考查的目的是理解掌握互质数的概念及意义.16.(•中山市模拟)质数只有1个因数.错误.(判断对错)考点:合数与质数.专题:整数的认识.分析:自然数中,除了1和它本身外,没有别的因数的数为质数.由此可知,质数共有2个因数,即1和它本身.解答:解:根据质数的意义可知,质数共有2个因数,即1和它本身.故答案为:错误.点评:自然数中,只有1只有一个因数,即它本身.17.(•上海模拟)既是合数又是偶数的最小自然数是4.考点:合数与质数;奇数与偶数的初步认识.分析:根据质数与合数、奇数与偶数的意义,是2的倍数的数叫做偶数;不是2的倍数的数叫做奇数;一个自然数如果只有1和它本身两个因数,这样的数叫做质数;一个自然数如果除了1和它本身还有别的因数,这样的数叫做合数;由此解答.解答:解:根据合数、偶数的意义,既是合数又是偶数的最小自然数是4.故答案为:4.点评:解答本题主要明确自然数,合数、质数、奇数、偶数的概念.18.(•贵州模拟)相同两个素数的和等于它们的积,这个素数是2.考点:合数与质数.专题:数的整除.分析:一个自然数如果只有1和它本身两个因数,这样的数叫做质数(素数),在所有的质数中,相同两个素数的和等于它们的积,得出2+2=2×2,所以这个素数是2.解答:解:相同两个素数的和等于它们的积,这个素数是2;故答案为:2.点评:此题考查了质数的含义.19.(•通州区模拟)一个非零自然数,不是质数就是合数.×.(判断对错)考点:合数与质数.专题:综合判断题.分析:根据质数与合数的意义:一个自然数,如果只有1和它本身两个因数,这样的数叫做质数;一个自然数,如果除了1和它本身还有别的因数,这样的数叫做合数;1既不是质数也不是合数.解答:解:因为,1既不是质数也不是合数,所以,一个非零自然数,不是质数就是合数.此说法是错误的.故答案为:×.点评:解答此题的关键是理解质数、合数的意义.20.(•临川区模拟)最小的质数占最小的合数的50%.考点:合数与质数;百分数的实际应用.专题:综合填空题.分析:最小的质数是2,最小的合数是4,进而用2除以4,计算得出百分数的结果即可.解答:解:最小的质数是2,最小的合数是4,那么:2÷4=0.5=50%.故答案为:50%.点评:明确求一个数占另一个数的百分之几,用除法计算;也考查了最小的质数是2,最小的合数是4.三.解答题(共10小题)21.两个质数的积一定是奇数,如3×5=15、11×83=913×.考点:合数与质数;奇数与偶数的初步认识.专题:数的整除.分析:在自然数中,除了1和它本身外,没有别的因数的数为质数,则最小的质数是2;能被2整数的数为偶数.由此可知,2与其它质数的积一定是偶数.解答:解:由于最小的质数是2,则2与其它质数的积一定是偶数.故答案为:×.点评:除了2之外,任意两个质数的积一定是奇数.22.判断27,28,29,30是素数,还是合数.考点:合数与质数.专题:数的整除.分析:在自然数中,除了1和它本身外,没有别的因数的数为质数.除了1和它本身外,还有别的因数的数为合数.据此分析即可.解答:解:在27,28,29,30中,素数为29,合数为27,28,30.点评:本题考查了学生对于合数与质数意义的理解与应用.23.写出大于85而小于98的所有素数.考点:合数与质数.专题:数的整除.分析:在自然数中,除了1与它本身之外,没有别的因数的数为质数.据此意义完成即可.解答:解:大于85而小于98的所有素数为:89、97.点评:完成本题要注意将大于85而小于98中的数分解质因数,以确定它们因数的个数.24.四个质数的乘积是和的11倍,这样的数和是多少?考点:合数与质数.专题:数的整除.分析:因为四个质数的乘积是和的11倍,可知四个数里面一定有一个是11,设其余三个是abc,那么abc=a+b+c+11,因为b+c≥4,所以11<3(b+c)容易知道b+c≤bc,因此abc<a+4bc,4≤bc<a/(a﹣4)或a<4得到a=2,3,5,同理b,c,据此解答即可.解答:解:4个质数的乘积是和的11倍,可知四个数里面一定有一个是11,设其余三个是abc,那么abc=a+b+c+11,因为b+c≥4,所以11<3(b+c)容易知道b+c≤bc,因此abc<a+4bc,4≤bc<a/(a﹣4)或a<4得到a=2,3,5,同理b=2,3,5,c=2,3,5,经过验证这4个质数为2,2,5,112+2+5+11=20答:这样的数和是20.点评:解答本题的关键是:四个质数的乘积是和的11倍,可以推算出期中一个质数是11.25.有一个三位数,百位数字是最小的质数,个位数是一位数中最大的偶数,这个数最小是多少?最大是多少?(直接写数)考点:合数与质数;奇数与偶数的初步认识.专题:整数的认识;数的整除.分析:我们知道最小的质数是2,一位数中最大的偶数是8.所以这个三位数百位上是2,个位上是8,要想最小,十位为0,最大十位为9,据此解答即可.解答:解:由分析可得这个数最小是208;最大是298.答:这个数最小是208;最大是298.点评:本题是考查整数的写法、质数与合数的意义、自然数的意义.26.我校少先队员排队做操,每排人数相等且都在1人以上.想一想,总共有多少人?在正确答案的下面划线.41人43人47人49人.考点:合数与质数.专题:数的整除.分析:由“每排人数相等且都在1人以上”说明总人数能分成几个相同的数,即合数;而41、43、47都是质数,故不能分成几个相同的数,因此总人数为49.解答:解:由题意,总人数能分成几个相同的数,而41、43、47都是质数,故不能分成几个相同的数,因此总人数为49.答:五(3)班有49人.点评:此题重点考查了合数与质数的概念,并由此解决问题.27.在横线填上合适的质数.10=3+736=17+1991=13×785=17×524=11+13=17+7.考点:合数与质数.专题:数的整除.分析:在自然数中,除了1和它本身外,没有别的因数的数为质数.据此意义将题目中的数分解成两个质数相加的形式即可.解答:解:10=3+736=17+1991=13×785=17×524=11+13=7+17故答案为:3,7;17,19;13,7;17,5;11,13,17,7.点评:如果两个质数的和是奇数,则这两个质数其中一个一定为2.28.写出60的全部因数,其中质数有2、3、5,偶数有2、4、6、10、12、20、30、60.考点:合数与质数;奇数与偶数的初步认识.专题:数的整除.分析:先根据找一个数因数的方法,找出60的所有因数,然后根据质数和合数的意义,奇数和偶数的意义进行分类.解答:解:60=1×60=2×30=3×20=4×15=5×12=6×10所以60的因数有1、2、3、4、5、6、10、12、15、20、30、60,在这些因数中,质数有2、3、5;偶数有2、4、6、10、12、20、30、60.故答案为:2、3、5,2、4、6、10、12、20、30、60.点评:熟练掌握找一个数因数的方法,以及正确的对自然数进行分类是解决本题的关键.B档(提升精练)一.选择题(共10小题)1.(•天河区)下面说法正确的是()A.两个质数的和一定是质数B.假分数的倒数都小于1C.分数的大小一定,它的分子和分母成正比例D.面积相等的两个三角形一定能拼成一个平行四边形考点:合数与质数;倒数的认识;分数的基本性质;三角形的周长和面积.专题:综合判断题.分析:根据题意,对各题进行依次分析、进而得出结论.解答:解:A、两个质数的和一定是质数,说法错误,如:3+5=8,8是合数;B、假分数的倒数都小于1,说法错误,如;C、因为:分子÷分母=分数的值(一定),它的分子和分母成正比例;D、因为:面积相等的两个三角形一定能拼成一个平行四边形,说法错误;故选:C.点评:此题涉及的知识点较多,但都比较简单,属于基础题,只要认真,容易完成,注意平时基础知识的积累.2.(•高台县)下列说法正确的是()A.1既不是质数也不是合数B.最小的合数是2C.负数比正数大考点:合数与质数;正、负数大小的比较.专题:整数的认识.分析:在自然数中,1既不是质数也不是合数;除了1和它本身外,没有别的因数的数为质数,除了1和它本身外,还有别的因数的数为合数;在数轴上,负数位于0的左边,正数位于0的右边,借助数轴比较数的大小,所有的负数都在0的左边,也就是负数都比0小,而正数都比0大,正数都比负数大.解答:解:下列说法正确的是:1既不是质数也不是合数.故选:A.点评:根据质数与合数,正数与负数的含义进行解答即可.3.(•泗县模拟)在1~25的自然数中,合数有()A.14 B.15 C.16考点:合数与质数.专题:压轴题.分析:根据合数的定义即可解决问题.解答:解:在1~25的自然数中合数有:4、6、8、9、10、12、14、15、16、18、20、21、22、24、25,共15个,故选:B.点评:此题考查了合数的定义.4.(•龙海市模拟)在1、2.3、2、6、﹣4、5%、23、9、51中,素数有()个.A.1个B.2个C.3个考点:合数与质数.专题:数的认识.分析:根据质数(又叫素数)的意义,一个自然数,如果只有1和它本身两个因数,这样的数叫做质数(素数).由此解答.解答:解:在1、2.3、2、6、﹣4、5%、23、9、51中,素数有:2,23.答:在这组数中素数有2和23.故选:B.点评:此题考查的目的是使学生理解质数(素数)的意义,明确质数与合数是在非0自然数范围内,根据一个非0自然数因数个数的多少分成质数、合数和1三部分.5.(•萝岗区)两个质数的积一定是()A.奇数B.偶数C.质数D.合数考点:合数与质数.专题:压轴题;数的整除.分析:在自然数中,除了1和它本身外,没有别的因数的数为质数.最小的质数是2,除了2之外,其它质数都为奇数.根据数的奇偶性可知,2与其它质数相乘的积一定是偶数;除了2之外,其它两个质数相乘的积是奇数,即两个质数的积可能是偶数也可是质数;又在自然数中,除了1和它本身外,还有别的因数的数为合数.两质数相乘的积的因数,除了1和它本身外,还有这两个质数是它的因数,即共有4个因数.一定为合数.解答:解:根据质数的意义及数的奇偶性可知,个质数的积可能是偶数也可是质数;根据合数的意义可知,两质数相乘的积,一定为合数.故选:D.点评:完成本题要注意最小的质数是2,2同时为偶数.6.(•楚州区)所有素数的积是()A.奇数素数B.奇数合数C.偶数合数D.偶数素数考点:合数与质数.专题:数的整除.分析:在自然数中,除了1和它本身外,没有别的因数的数为质数.则最小的质数是2,除了1和它本身外,还有别的因数的数为合数.由于素数有无数个,则所有所有素数的积的因数也有无数个,则它们的积是合数,又最小的素是2,2为偶数,根据数的奇偶性可知,所有素数的积是偶合数.解答:解:所有所有素数的积的因数也有无数个,则它们的积是合数,又最小的素是2,2为偶数,根据数的奇偶性可知,所有素数的积是偶合数.故选:C.点评:除了2之外,所有素数为奇数,则除2之外所有素数的积是奇数合数.7.(•玉溪模拟)在下面与3有关的四句话中,正确的一句话是()A.3是一个自然数,它既是质数也是奇数B.一个自然数的末位是3的倍数,这个自然数一定能被3整除C.任何一个偶数都能被2整除,但不能被3整除D.如果m是一个不为零的自然数,那么3和m一定是互质数考点:合数与质数;奇数与偶数的初步认识;找一个数的倍数的方法.专题:数的整除.分析:根据所学的有关知识,将下列四个选项逐一进行分析、判断,即可选择出正确的一项.解答:解:A、根据自然数、质数、奇数的定义可知,3是一个自然数,它既是质数也是奇数,所以此选项说法正确;B、举例说明:如26,末位数字是6,是3的倍数,但是这个自然数26不能被3整除,所以此选项说法错误;C、举例说明:24,是偶数,能被2整除,也能被3整除,所以此选项说法错误;D、互质数是指两个数的最大公因数是1,如果m=21,则3和m的最大公约数是3,所以不是互质数,此选项说法错误.故选:A.点评:此题主要考查质数、倍数、奇数、偶数、互质数的意义及应用,此类问题可以采用举反例的方法进行判断选择.8.(•天河区)两个数既是合数,又是互质数,它们的最小公倍数是90,这两个数分别是()A.9和10 B.2和45 C.6和15 D.30和3考点:合数与质数;求几个数的最小公倍数的方法.专题:数的整除.分析:在自然数中,除了1和它本身外还有别的因数的数为合数.公因数只有1的两个数为互质数.又互质的两个数的最小公倍数一定是这两个互质数相乘的积,据此分析即可.解答:解:由于90=2×45=18×5=15×6=9×10,在这几组数中,2、5不是合数,15与6不互质,符合条件的只有10与9,故选:A.点评:明确互质的两个数的最小公倍数一定是这两个互质数相乘的积并据此分析是完成本题的关键.。
第3讲质数与合数内容概述:掌握质数与合数的概念;熟悉常用的质数,并掌握质数的判定方法;能够利用分解质因数的方法解决相关的整数问题;学会计算末尾零的个数。
典型问题:兴趣篇1.(1)如果两个质数相加等于16,这两个质数有可能等于多少?(2)如果两个质数相加等于25,这两个质数有可能等于多少?(3)如果两个质数相加等于29,这样的两个质数存在吗?【分析】(1)因为16是个偶数,偶等于偶+偶或是奇+奇,但是质数中只有2是偶数,所以只能是奇+奇,所以是3+13或是5+11(2)因为25是个奇数,奇等于偶+奇,但是质数中只有2是偶数,所以另一个是25-2=23 (3)因为29是个奇数,奇等于偶+奇,但是质数中只有2是偶数,所以另一个只能是29-2=27,但是27不是质数,所以不存在!(第1届华罗庚金杯数学邀请赛决赛二试试题)2.有个人说:“任何7个连续数中一定有质数”。
请你举一个例子,说明这句话是错的。
【分析】方法一:例100以内:90-96,100以上很多,例114-126。
方法二:又例如连续的7个整数:842、843、844、845、846、847、848分别能被2、3、4、5、6、7、8整除,也就是说它们都不是质数.评注:有些同学可能会说这是怎么找出来的,翻质数表还是……,我们注意到(n+1)!+2,(n+1)!+3,(n+1)!+4,…,(n+1)!+(n+1)这n个数分别能被2、3、4、…、(n+1)整除,它们是连续的n 个合数.其中n !表示从1一直乘到n 的积,即1×2×3×…×n .3. 请写出5个质数,使得它们正好构成一个公差为12的等差数列。
【分析】10以上质数的末位只能是1,3,7,9.,一个数的末位+2只能出现1,3,7,9,那么这个数最小不能是偶数,不能是3,所以可以试验5,5+12=17,17+12=29,29+12=41,41+12=53,即可满足要求。
1. 掌握质数与合数的定义2. 能够用特殊的偶质数2与质数5解题3. 能够利用质数个位数的特点解题4. 质数、合数综合运用一、质数与合数 一个数除了1和它本身,不再有别的约数,这个数叫做质数(也叫做素数).一个数除了1和它本身,还有别的约数,这个数叫做合数。
要特别记住:0和1不是质数,也不是合数。
常用的100以内的质数:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97,共计25个;除了2其余的质数都是奇数;除了2和5,其余的质数个位数字只能是1,3,7或9.考点:⑴ 值得注意的是很多题都会以质数2的特殊性为考点.⑵ 除了2和5,其余质数个位数字只能是1,3,7或9.这也是很多题解题思路,需要大家注意.二、判断一个数是否为质数的方法根据定义如果能够找到一个小于p 的质数q (均为整数),使得q 能够整除p ,那么p 就不是质数,所以我们只要拿所有小于p 的质数去除p 就可以了;但是这样的计算量很大,对于不太大的p ,我们可以先找一个大于且接近p 的平方数2K ,再列出所有不大于K 的质数,用这些质数去除p ,如没有能够除尽的那么p 就为质数.例如:149很接近1441212=⨯,根据整除的性质149不能被2、3、5、7、11整除,所以149是质数.模块一、判断质数合数 【例 1】 下面是主试委员会为第六届“华杯赛”写的一首诗:美少年华朋会友,幼长相亲同切磋;杯赛联谊欢声响,念一笑慰来者多;九天九霄志凌云,九七共庆手相握;聚起华夏中兴力,同唱移山壮丽歌.请你将诗中56个字第1行左边第一字起逐行逐字编为1—56号,再将号码中的质数由小到大找出来,例题精讲知识点拨知识框架5-3-1.质数与合数(一)将它们对应的字依次排成一行,组成一句话,请写出这句话.【考点】判断质数合数【难度】1星【题型】填空【解析】按要求编号排序,并画出质数号码:美少年华朋会友,幼长相亲同切磋;1 2 3 4 5 6 7 8 9 10 11 12 13 14杯赛联谊欢声响,念一笑慰来者多;15 16 17 18 19 20 21 22 23 24 25 26 27 28九天九霄志凌云,九七共庆手相握;29 30 31 32 33 34 35 36 37 38 39 40 41 42聚起华夏中兴力,同唱移山壮丽歌.43 44 45 46 47 48 49 50 51 52 53 54 55 56将质数对应的汉字依次写出就是:少年朋友亲切联欢;一九九七相聚中山.【答案】少年朋友亲切联欢;一九九七相聚中山【例 2】著名的哥德巴赫猜想是:“任意一个大于4的偶数都可以表示为两个质数的和”。
五年级数学质数与合数试题答案及解析1.两个质数的积一定是合数。
()【答案】√【解析】略2.把10以内所有的质数相乘,所得的积一定是( )。
A.奇数B.偶数C.质数D.无法确定【答案】B【解析】略3. 12的因数有( ),其中( )是质数,( )是合数。
【答案】1,2,3,4,6,12 2,3 4,6,12【解析】略4.在20以内的自然数中,是奇数又是质数的数是()。
【答案】3,5,7,11,13,17,19【解析】略5.两个质数的差是2,这两个质数分别是( )和( )。
【答案】7 5【解析】略6.最小的质数是( ),最小的奇数是( ),( )既不是质数也不是合数。
【答案】2 1 1【解析】略7.两个质数的和一定是合数。
( )【答案】×【解析】例如2+3=5,5是质数。
8. 37是( )。
A.因数 B.质数 C.合数【答案】B【解析】略9.按要求写数。
24的因数:___________________________________________40以内6的倍数:______________________________________20以内的质数:________________________________________20以内的合数:_______________________________________20以内的奇数:_______________________________________20以内的偶数:_______________________________________【答案】24,2,12,3,8,4,66,12,18,24,30,362,3,5,7,11,13,17,194,6,8,9,10,12,14,15,16,18,201,3,5,7,9,11,13,15,17,192,4,6,8,10,12,14,16,18,20【解析】略10.如果n是自然数,那么2n+2一定是偶数。
第3讲质数与合数阿拉伯数字无疑是人类历史上最伟大的发明之一,其本身蕴含的规律更是数学学科中最璀璨的明珠!质数和合数的分类产生了哥德巴赫猜想等世界著名的命题,学习质数和合数,窥探数字的奥秘!对于自然数a 和b (0b ≠),若a b ÷没有余数,则a 是b 的倍数,b 是a 的约数。
特殊地,0是任意非零自然数的倍数。
质数:除了1和本身,没有其他约数的自然数叫质数。
合数:除了1和本身,还有其他约数的自然数叫合数。
特殊地,1既不是质数也不是合数。
最小的合数是4,最小的质数是2,且2是唯一的偶质数。
质因数:如果一个质数是某个数的约数,那么就说这个质数是这个数的质因数。
互质数:公约数只有1的两个自然数,叫做互质数。
分解质因数:把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
编写说明知识要点【例1】对7个不同质数求和,和为58,则最大的质数是多少?【分析】七个质数若全部是奇数,则和一定是奇数,而58是偶数,则七个质数中必定含有唯一的偶质数2,所以最小的质数是2,从2开始,最小的七个连续质数是2,3,5,7,11,13,17,和为58,所以题中的七个质数只能是从2开始的七个连续质数,最大为17。
【温馨提示】2是唯一的偶质数,是偶数中的“叛徒”,所以质数也经常与奇偶性相结合,主要考察“2”.【拓展】已知a、b、c、d都是质数,且130959179+=+=+=+,求a、b、c、d的值。
a b c d【分析】959179+=+=+,所以b、c、d应该都是奇数,所以a是唯一的偶质数2,依此可求得:b c dc=,53b=,41d=.a=,372【例2】从小到大写出5个质数,使后面数都比前面的数大12。
这样的数有几组?【分析】考虑到质数中除了2以外其余都是奇数,因此这5个质数中不可能有2;又质数中除了2和5,其余质数的个位数字只能是1、3、7、9。
若这5个质数中最小的数其个位数字为1,则比它大24的数个位即为5,不可能是质数;若最小的数其个位数字为3,则比它大12的数个位即为5,也不可能为质数;由此可知最小的数其个位数字也不可能是7和9,因此最小的数只能是5,这5个数依次是5,17,29,41,53。
这样的数只有一组。
说明:除了2和5,其余的质数个位数字只能是1,3,7或9。
这是此题的突破口。
老师可以只推算个位数字就可以否定1、3、7、9,然后剩下个位数字是2和5,就很容易找到5。
【拓展】如果某整数同时具备如下三条性质:①这个数与1的差是质数,②这个数除以2所得的商也是质数,③这个数除以9所得的余数是5,那么我们称这个整数为幸运数。
求出所有的两位幸运数。
【分析】法一:由条件②可知,所求的数是偶数,因此可设所求的幸运数是质数p的两倍,即此幸运数为2p,则p的所有可能取值为5,7,11,13,17,19,23,29,31,37,41,43,47。
于是2p-1的所有可能取值为9,13,21,25,33,37,45,57,61,73,81,85,93。
根据题目条件①,2p-1应为质数,因此2p-1只可能为13,37,61或73。
再由条件③知2p-1除以9所得的余数应为4,于是2p-1只可能是13,从而这个幸运数只能是2p=14。
法二:从条件③入手,符合条件的偶数有:14,32,50,68,86,再由条件②排除掉32,50,68,最后由条件①排除掉86,所以这个幸运数是14。
【例3】四个连续自然数的乘积是3024,这四个自然数中最大的一个是多少?【分析】分解质因数43=⨯⨯,考虑其中最大的质因数7,说明这四个自然数中必定有一个是7的3024237倍数。
若为7,因3024不含有质因数5,那么这四个自然数可能是6、7、8、9或7、8、9、10(10仍含有5,不行),经检验6、7、8、9恰符合。
【温馨提示】根据乘积求因数,是分解质因数的一个重要运用.【拓展】2004×7×20的计算结果能够整除三个连续自然数的乘积,这三个连续自然数之和最小是多少?【分析】首先分解质因数,2004×7×20=2×2×2×2×3×5×7×167,其中最大的质因数是167,所以所要求的三个连续自然数中必定有167本身或者其倍数。
165=3×5×11,166=2×83,168=2×2×2×3×7,169=13×13,所以165×166×167,166×167×168,167×168×169都没有4个2,不满足题意。
说明167不可行。
尝试334=167×2,335=5×67,336=2×2×2×2×3×7,334×335×336=2×2×2×2×2×3×5×7×67×167,包括了2004×7×20中的所有质因数,所以这组符合题意,以此三数之和最小为1005。
【拓展】 甲数比乙数大5,乙数比丙数大5,三个数的乘积是6384,求这三个数。
【分析】 将6384分解质因数,6384=22223719⨯⨯⨯⨯⨯⨯,则其中必有一个数是19或19的倍数;经试算,19-5=14=2×7,19+5=24=2×2×2×3,恰好14×19×24=6384,所以这三个数即为14,19,24。
一般象这种类型的题,都是从最大的那个质因数去分析。
如果这道题里19不符合要求,下一个该考虑38,再下一个该考虑57,依此类推。
【例4】 一个长方体的长、宽、高是连续的3个自然数,它的体积是39270立方厘米,那么这个长方体的表面积是多少平方厘米?【分析】 方法一:39270=2×3×5×7×11×17,为三个连续自然数的乘积,所以33、34、35为满足题意的长、宽、高.则长方体的表面积为:2×(长×宽+宽×高+高×长)=2×(33×34+34×35+35×33) =6934(平方厘米).方法二:39270=2×3×5×7×11×17,为三个连续自然数的乘积,考虑质因数17,如果17作为长、宽或高显然不满足.当17与2结合即34作为长方体一条边的长度时有可能成立,再考虑质因数7,与34接近的数32~36中,只有35含有7,于是7与5的乘积作为长方体的一条边的长度.而39270的质因数中只剩下了3和1l ,所以这个长方体的大小为33×34×35.长方体的表面积为: 2×(3927033+3927034+3927035)=2×(1190+1155+1122)=2×3467=6934(平方厘米).【拓展】 在面前有一个长方体,它的正面和上面的面积之和是209,如果它的长、宽、高都是质数,那么这个长方体的体积是多少?【分析】 如上图,设长、宽、高依次为a 、b 、c ,有正面和上面的和为209ac ab +=.()209ac ab a c b +=⨯+=,而2091119=⨯.当11a =时,19c b +=,当两个质数的和为奇数,则其中必定有一个数为偶质数2,则217c b +=+;当19a =时,11c b +=,则29c b +=+,b 为9不是质数,所以不满足题意.所以它们的乘积为11217374⨯⨯=.【例5】 4只同样的瓶子内分别装有一定数量的油.每瓶和其他各瓶分别合称一次,记录千克数如下:8,9,10,11,12,13.已知4只空瓶的重量之和以及油的重量之和均为质数,求最重的两瓶内有多少油? 【分析】 由于每只瓶都称了三次,因此记录数据之和是4瓶油(连瓶)重量之和的3倍,即4瓶油(连瓶)共重(8+9+10+11+12+13)÷3=21(千克)而油重之和及瓶重之和均为质数,所以它们必为一奇一偶,由于2是唯一的偶质数,只有两种可能:(1)油重之和为19千克,瓶重之和为2千克,每只瓶重21千克,最重的两瓶内的油为13-12×2=12(千克).(2)油重之和为2千克,瓶重之和为19千克,每只瓶重194千克,最重的两瓶内的油为13-194×2=27(千克),这与油重之和2千克矛盾.因此最重的两瓶内共有12千克油.【例6】从20以内的质数中选出6个,然后把这6个数分别写在正方体木块的6个面上,并且使得相对两个面的数的和都相等。
将这样的三个木块掷在地上,向上的三个面的三个数之和可能有多少种不同的值?【分析】小于20的质数有2,3,5,7,11,13,17,19,其中5+19=7+17=11+13。
每个木块掷在地上后向上的数可能是六个数中的任何一个,三个数的和最小是5+5+5=15,最大是19+19+19=57,经试验,三个数的和可以是从15到57的所有奇数,所有可能的不同值共有22个。
【拓展】有些自然数能够写成一个质数与一个合数之和的形式,并且在不计加数顺序的情况下,这样的表示方法至少有13种,那么所有这样的自然数中最小的一个是多少?【分析】在所有的质数中,从小到大第13个质数是41,因此在13种分解方法中,质数最大的那一组至少是41445+=。
按题目要求分拆45有如下12种方法:4534254073811341332=+=+=+=+=+ =+=+=+=+=+=+=+17281926232229163114378414按题目要求分拆46有如下7种方法:=+=+=+=+=+=+=+462447391135133319273115379按题目要求分拆47有如下14种方法:=+=+=+=+=+=+=+472453444435426417401037=+=+=+=+=+=+=+因此满足题意的最小自然数是47。
1136133417301631182919282324【练习1】4个一位数的乘积是360,并且其中只有一个是合数,那么在这4个数字所组成的四位数中,最大的一个是多少?【分析】将360分解质因数得360=2×2×2×3×3×5,它是6个质因数的乘积。
因为题述的四个数中只有一个是合数,所有该合数必至少为6-3=3个质因数的积,又只有3个2相乘才能是一位数,所以这4个乘数分别为3,3,5,8,所组成的最大四位数是8533。