曲线要素计算程序

万能程序包含所有曲线要素的万能测量程序（6种模式）扩展变量操作（15个）：Defm 15 , O字母0数字←┚J-SQX（竖曲线数据输入）“J-SQX”:{NHUVMQP}:Z[9]=N“SJD”:Z[10]=H“JDZ”:Z[11]=U“I1”:Z[12]=V“I2”:Z[13]=M“R”:Z[14]=Q“QD”:Z[15]=P“ZD”:“T O J-JSMS”J-PQX (平面数据输入，自行切换到J-JSMS)A“JD” B“JDX” C“JDY” F“FJ” O“ZJ：Z-，Y+” RE“LS1”K“LS2”：E<1=>E=1E-9⊿K<1=>K=1E-9⊿Z[1]=EE÷24R-E∧4÷2688RRR:Z[2]=E÷2-EEE÷240RR:X=(EE-KK)÷24R÷sin Abs O :Z[3]“T1”=(R+Z[1])tan(Abs O÷2)+Z[2]-X◢Z[4]“T2” =(R+KK÷24R-K∧4÷2688RRR)tan(Abs O÷2)+K÷2-KKK÷240RR+X◢L=Abs OπR÷180+(E+K)÷2◢J=tan-1((R+Z[1])÷(Z[3]-Z[2]):X“E”=(R+Z[1])÷sin J-R◢X=A-Z[3]:Y=X+E:E<1=>X“ZY”◢≠=>X“ZH”◢Y“HY”◢⊿Y“QZ”=X+(L-K-E)÷2+E◢Y=X+L-K:X=X+L:K<1=>X“YZ”◢≠=>Y“YH”◢X“HZ”◢⊿Prog“J-JSMS” ←┚J-JSMS（放样模式主程序）“1-ZS,2-F1,3-FS”:“4-F2,5-Z0,6-DM”:Lb1 0:{Z}:Z“MS”≤2=>Goto 1: ≠=> Z≤4=> Goto2:≠=> Goto 3⊿⊿←┚Lb1 1 :{PDW}:PD“BZ”W“BJ”: Prog“JP”:X“X=”◢(4850输入“X=”：X◢)Y“Y=” ◢(4850输入“Y=”：Y◢)Z<2=> Goto 1:≠=>Prog“JS”:Prog“JC”:H“Z”=H+G◢Goto 1⊿←┚Lb1 2 :{XYW}:XYW“BJ”: Prog“JF”: P“P=”◢(4850输入“P=”：P◢)D“BZ=”◢(4850输入“BZ=”：D◢)Z<4=>Goto2:≠=>{Q}:Q“ZP”:Prog“JS”:Prog“JC”:Prog“JB”:Goto2⊿←┚Lb1 3 :{P}:P: Prog“JS”:H“Z0=”◢(4850输入“Z0=”：H◢)Z<6=>Goto3:≠=>{D}:S“CGZ”:T“JKZ”:Z[8]=Q“LH”:D“BZ”:Prog“JC”:J “JK=”◢(4850输入“JK=”：J◢)G“Z”=H+G◢(4850输入“Z=”：G=H+G◢)Goto 0⊿JS（竖曲线计算子程序）P<Z[14]=>Prog“J-S QX” ⊿P>Z[15]=>Prog“SJ-SQX”⊿←┚N=Z[9]:U=Z[11]:V=Z[12]:H=Z[13]:G=HAbs(U-V)÷200:P<N=>I=U:M=N-G:M>P=>M=P⊿≠=>I=V:M=N+G:M<P=>M=P⊿⊿J=(P-M)2÷2H:U-V>0=>J=-J⊿H=Z[10]+(P-N)×I ÷100+JJP（平曲线正算子程序）Fixm←┚Lb1 1 :J=F:X= B-Z[3]cos F :Y= C-Z[3]sin F :G=E←┚P≤A-Z[3]=>I=A-Z[3]-P:M=-I:N=0:H=F+W:Goto 5←┚≠=>P≤A-Z[3]+E=>I=P-A+Z[3]:H=90II÷REπ:O<0=>H=-H⊿H=H+W+F:G oto 3←┚≠=>P≤A-Z[3]+L-K=>I=P-A+Z[3]-E:Goto 4: ≠=>Goto 2⊿⊿←┚ Lb1 2 :X= B+Z[4]cos(F+O :Y= C+Z[4]sin(F+O :J=F+O+180:G=K←┚ P≤A-Z[3]+L=>I=A-Z[3]+L-P:H=90II÷RKπ:O>0=>H=-H⊿H=H+J+W+180 :Goto 3 ←┚≠=>I=P-A+Z[3]-L:M=-I:N=0:H=J+W+180:Goto 5 ←┚Lb1 3 :M=I-I∧5÷40RRGG:N=III÷6GR-I∧7÷336RRRGGG:Goto 5 ←┚ Lb1 4 :H=(E+2I)×90÷πR:M=R sin H+Z[2]:N=R(1-cosH)+Z[1]:O<0=>H=-H⊿H=J+H+W: Goto 5←┚Lb1 5 :P≤A-Z[3]+L-K=> O<0=>N=-N⊿≠=>O>0=>N=-N⊿⊿Goto 6←┚ Lb1 6 :X =X+M cos J-N sin J+D cos H:Y =Y+M sin J+N cos J+D sin HJF（平曲线反算子程序）Fixm←┚U=X:V=Y:D=0:J=F-W:P=A+(Y-C)cos J-(X-B)sin J←┚Lb1 1:Prog“JP”:J=H-180:I=(V-Y)cos J-(U-X)sin J:AbsI<1E-4=>Goto 2:≠=>P=P+I:Goto 1⊿←┚Lb1 2: D=(V-Y)÷s inHJC（超高加宽计算子程序）Fixm:Z[8]<1=>Z[8]=1E-8⊿I=E:M=A-Z[3]:E<1=>I=Z[8]:M=M-I⊿G=K:N=A-Z[3]+L:K<1=>G=Z[8]:N= N+G⊿←┚P≤0.5(N+M=>U=(P-M)÷I:≠=>U=(N-P)÷G⊿U<0=>U=0⊿U>1=>U=1⊿J=UT 高次抛物线加宽J=T(1-3UU+2UUU ) : D O<0=>J=0⊿I=1:Prog“JD”:I=US:G=I+UN-N:U=AbsD-V:U<0=>U=O⊿U>M+J+Z[5]=>U=M+J+Z[5]⊿Z[7]=1=>Goto 1:≠=>Goto 2←┚Lb1 1:I=G:D O>0=>I=-I:Abs I<N=>I=-N⊿⊿G=UI:N=I:Goto 3←┚Lb1 2:N<I=>N=I⊿G=N(M-U)+Z[5]Z[6]:N=-N:D O<0=>G=G+2IU:N=I⊿Goto 3←┚Lb1 3: U= M+J+V+Z[5]:Abs D≥U-0.01=>G=G-Z[5](N+Z[6])⊿JB（路基边桩放样子程序）H=H+G-Q:H<0=>I=2:H“W=”=Abs H◢≠=>I=3 :H“T=”◢(4850输入“T=”：H◢)⊿Prog“JD”:G=H÷V:G<1=>I=MG:≠=>G<2=>I=M+N(G-1):≠=>I=M+N+Z[6](G-2) ⊿⊿I“BP”=Abs D-VI-Z[7]Int G-U-Z[5] ◢G=V Frac G:G<1.5=>G“PT”◢⊿JD（断面数据储存子程序）I=1=>M=27:N=0.002:Z[5]=0.5:Z[6]=0.002:V=1.5:Z[7]=1:≠=> I=2=> Z[5]=0.8: M=0.75: N= 0.75: Z[6]=1.00: V=8: Z[7]=2.0 :≠=> Z[5]=0.3:M=1.50: N=1.75: Z[6]=2.00 : V=8: Z[7]=2.0⊿⊿ 符号说明：←┚◢⊿≠=> => ≤≥一、程序简介本套程序是共有2个主程序，7个子程序。

一、曲线要素计算已知：JDZH 、JDX 、JDY 、R 、L S1、L S2、L H 、T 、A 1、A 2（L H =L S1+L S2+圆曲线长）1、求ZH 点（或ZY 点）坐标及方位角⎪⎩⎪⎨⎧-=-=-=11sin cos AT JDY ZHY A T JDX ZHX TJDZH ZHZH 2、求HZ 点（或YZ 点）坐标及方位角⎪⎩⎪⎨⎧+=+=+-=22sin cos AT JDY HZY A T JDX HZX L T JDZH HZZH H3、求解切线长T 、外距E 、曲线长L（1）圆曲线⎪⎩⎪⎨⎧=-==180/)1)2/cos(/1()2/tan(απααR L R E R T （2）缓圆曲线 )2/(2/)2/cos(/)(2180/)21()2/tan()(020R l l l Rl l R p R E l R L qp R T s s s HsH H ===⎪⎩⎪⎨⎧-+=+⨯-=+⨯+=ββαπβα时当其中 二、直线上各桩号坐标及方位角计算 已知：ZH 、X 、Y 、A ⎪⎩⎪⎨⎧+=+==-=A L Y DY A L X DX A T ZH DZH L sin cos 三、第一缓和曲线上各桩号点坐标及方位角计算 已知：ZHZH 、ZHX 、ZHY 、A 1、R 、L S1、i （Z+1Y-1） ⎪⎩⎪⎨⎧⨯-+=⨯++=⨯⨯-==-=-=1111121132125cos sin sin cos /180)2/()6/()40/(Ay i A x ZHY DY A y i A x ZHX DX Rl l i A T Rl L y l R L L x ZHZH DZH L s s s π四、圆曲线上各桩号点坐标及方位角计算已知：ZHZH 、ZHX 、ZHY 、A 1、R 、L S1、i （Z+1Y-1）⎪⎩⎪⎨⎧⨯-+=⨯++=⨯+⨯-=⎪⎩⎪⎨⎧=-==++-=-++=--=1111121231110211231111cos sin sin cos /180)/2/(24/240/2/2/24/)]/2/cos(1[240/2/)/2/sin(Ay i A x ZHY DY A y i A x ZHX DX R L R l i A T R l p R l l q R l R l R L R l R y R l l R L R l R x ls ZHZH DZH L s s s s s s s s s s πβ其中五、第二缓和曲线上个桩号坐标及方位角计算 已知：HZZH 、HZX 、HZY 、A2、R 、L S2、i （Z+1Y-1） ⎪⎩⎪⎨⎧⨯--=⨯+-=⨯⨯+==-=-=2222222232225cos sin sin cos /180)2/()6/()40/(Ay i A x HZY DY A y i A x HZX DX Rl l i A T Rl L y l R L L x DZHHZZH L s s s π六、边桩坐标求解 已知：DZH 、X 、Y 、T 、BZJL （Z+Y-）、DLJJ 、N （距中桩距离，左正右负）⎪⎩⎪⎨⎧-=-=+=T N Y BDY T N X BDX T T sin cos α七、纵断面高程计算（1） 直线段上高程计算 已知：直线上任一点桩号（ZH ）、高程（H ）、纵坡（i ）)(*ZH DZH i H DH -+=（2） 竖曲线上高程计算已知：竖曲线起点桩号（ZH ）、起点高程（H ）、竖曲线半径R 、起点坡度（i ）、k （凸曲线+1、凹曲线-1） )2/(2R l k il H DH ZHDZH l ⨯-+=-=注：JDZH 、JDX 、JDY ：交点桩号、交点X 、Y 坐标R 、L S1、L S2：半径、缓和曲线1、缓和曲线2LH ：缓和曲线1长 +圆曲线长+ 缓和曲线2长 A1、A2：方位角1、方位角2 T ：在曲线要素中代表切线长；在坐标计算中代表被求解点的坐标方位角。

圆曲线要素计算公式
1圆曲线要素
圆曲线是一种比较复杂的曲线，一般表示一个圆曲线就需要四组参数，它们分别是锚点、大小、旋转角度和方向。

2圆曲线计算公式
圆曲线(or圆弧)曲线在数学上表示为:(x-Cx)^2+(y-Cy)^2= r^2。

这个公式中，Cx和Cy分别是圆心横纵坐标，r代表半径，可以通过计算得出圆曲线。

3圆曲线应用
圆曲线在计算机图形学中有重要的应用，它把平面上的点连接起来，形成一条由点变王的曲线。

这条曲线往往用于表示更复杂的几何体，如圆、椭圆、三角形、多边形等等。

4圆曲线的优势
圆曲线的优势在于它的计算精度高，圆曲线上的每个点处，都可以接近圆形。

而且，由于圆曲线本身就很接近于圆，而且它又具有良好的扩展性，所以可以用来做不同程度圆形的几何体。

5结论
圆曲线能够把一个平面上的点连接成一条曲线，而且可以通过圆曲线的计算公式更好的表示几何体的形状与形态，它在数学计算以及计算机图形学中有着重要的应用。

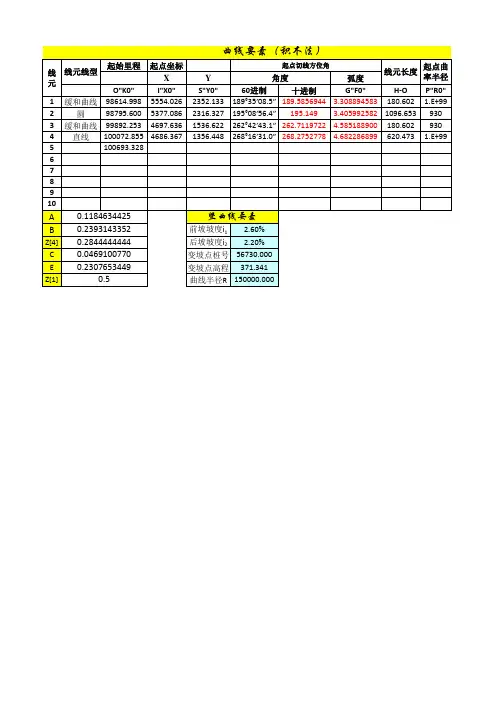
竖曲线1、竖曲线要素计算1.)变坡角δ：相邻两纵坡i1，i2，由于公路纵坡的允许值不大，故可以认为变坡角δ为：δ=△i= i1-i2（若不考虑近似情况，该值δ=arctan (i1)-arctan(i2)。

需要注意的是假设坡度上升为正时，δ计算结果会有正有负，但其绝对值的大小却与变坡角的角度相等。

但若不考虑正负差异，会造成最终的计算结果出错。

）2.)切线长T：（变坡角δ和圆心角大小相等。

）由于δ很小，可认为故（若不考虑近似情况，,δ值的正负号需注意。

）3.)曲线长L的计算由于变坡角δ很小，可认为L=2T（若不考虑近似情况，因为δ等于该弧所对应的圆周角，那么L=R*δ，其中δ应换算成弧度。

注意在利用CASIO计算器计算时的中间、最终结果的角度弧度问题。

）4.)外矢距E的计算由于变坡角δ很小，可认为y坐标与半径方向一致，它是切线上与曲线上的高程差。

从而得（R+y）2=R2+x2展开2Ry=x2-y2又因y2 与x2相比较，y2的值很小，略去y2，则2Ry= x2即当x=T时，y值最大，约等于外矢距E，所以（若不考虑近似情况，y2+2Ry-x2=0，，其中E >0,。

）2、竖曲线的测设算例：已知：某竖曲线半径R=2000米，相邻坡段的坡度i1=-2.95%，i2=-5.0628%，变坡点里程桩号为K0+760，其高程为428.312米。

（设计给出T=21.128，E=0.112。

）求：K0+730、K0+740、K0+750、K0+760、K0+770、K0+780、K0+790的线路坡度高程和设计高程。

解：步骤一：由已知条件知δ= i1-i2=-0.0295+0.050628=0.021128弧度（若不考虑近似情况δ=（arctan(i1)-arctan(i2)）=1°12′30.82″=0.0210940493155弧度）1、）切线长=1000*（-0.0295+0.050628）=21.128米（若不考虑近似情况，=21.0942米）2、）曲线长L=2T=21.128*2=42.256米（若不考虑近似情况L=R*δ=2000*（arctan(i1)-arctan(i2)）=2000*1°12′30.82″*π/180°=42.1867米）3、）外矢距=21.128^2/4000=0.1116米(若代入T=21.0942，计算结果=0.1112)（若不考虑近似情况 =0.1112米，其中T=21.0942。

公路工程的圆曲线要素代表的含义、计算式
图1 圆曲线要素的示意图
一、圆曲线各要素对应于图1的含义：
1．半径：圆的半径，对应于图1中的R
2．切线长度T：图1中，圆曲线左切点A至切线交点C之间的直线长度（对应于图1中AC 直线长度）
3．曲线长度L：A、B两点间的圆弧长度，图1中的弧线L。

4．转角值2a：两条切线AC和BC之间夹角的补角（即图1中的2a），也等于OA和OB之间的夹角。

5．外距：C点到圆弧的最小距离，即图1中CD的长度。

二、圆曲线要素之间的关系：
由图1可知,
1.转角(a)和切线长度(T)、半径之间(R)的关系：
，或者：a=arctan()
这里得到的角度单位是弧度，即180度等于弧度单位的PI（3.141592……），对此不太理解的童鞋，请复习高中数学的三角函数有关章节。

2. 弧长(L)和转角(a)的关系
L=R*a
=R*arctan()
3. 外距CD
CD=R*()。

铁路圆曲线要素计算程序设计
要设计一个计算铁路圆曲线要素的程序，可以按以下步骤进行设计：
1. 确定输入要素：
- 初始点：曲线起点的坐标或里程
- 终点：曲线终点的坐标或里程
- 曲线半径：圆曲线半径
- 速度限制：曲线上的速度限制，可以根据需要选择是否加入
2. 确定输出要素：
- 曲线长度
- 运行速度表
- 中点坐标或里程
- 曲线的几何元素（切线长、长外矢量等）
3. 编写计算曲线长度的函数：
- 使用两点间的距离公式计算初始点和终点之间的直线距离 - 使用圆弧的长度公式计算曲线长度
4. 编写计算运行速度表的函数（可选）：
- 根据速度限制计算曲线上各点的速度限制
- 可以采用规定的速度限制表，或者根据某种规则计算速度限制
5. 编写计算中点坐标或里程的函数：
- 使用初始点和终点的坐标或里程计算曲线的中点坐标或里程
- 使用初始点和终点的坐标计算切线方向，然后计算中点的坐标
6. 编写计算几何元素的函数：
- 利用曲线半径和切线长公式计算切线长
- 利用切线长和圆曲线半径公式计算长外矢量
7. 设计主程序：
- 获取用户输入的初始点、终点、曲线半径和速度限制
- 调用计算曲线长度的函数，将结果保存
- 调用计算运行速度表的函数，将结果保存（可选）
- 调用计算中点坐标或里程的函数，将结果保存
- 调用计算几何元素的函数，将结果保存
- 输出计算结果
以上是一个简单的程序设计框架，具体的实现可以根据实际情况进行适当调整和优化。

平曲线的五大要素计算公式以下是关于平曲线的五大要素计算公式。

平曲线是指在平面上描述一条曲线的五种基本参数，包括曲线长度、曲线半径、曲线角度、曲线切线和曲线弧度。

下面是这五种要素的计算公式：1.曲线长度（L）：曲线长度可以通过计算曲线上的所有坐标点之间的距离来获得。

对于参数方程表示的曲线，曲线长度L可以通过以下公式计算：
L=∫(√((dx/dt)²+(dy/dt)²)dt)
其中，(dx/dt)和(dy/dt)分别是曲线在x和y方向上的速度矢量。

2.曲线半径（R）：曲线半径表示曲线在某一点处弯曲的程度。

对于圆弧曲线，曲线半径R可以通过以下公式计算：
R=(dx²+dy ²)^(1/2)/(1+(dy/dx)²)^(1/2)
其中，(dx,dy)是曲线上的某一点坐标。

3.曲线角度（θ）：曲线角度表示曲线在某一点处与x轴的夹角。

对于参数方程表示的曲线，曲线角度θ可以通过以下公式计算：
θ=atan2(dy/dx)
其中，(dx,dy)是曲线上的某一点坐标。

4.曲线切线（T）：曲线切线表示曲线在某一点处的切线方向。

对于参数方程表示的曲线，曲线切线T可以通过以下公式计算：
T=(dx/dt,dy/dt)
其中，(dx/dt)和(dy/dt)分别是曲线在x和y方向上的速度矢量。

5.曲线弧度（α）：曲线弧度表示曲线在某一点处沿逆时针方向的旋转程度。

对于圆弧曲线，曲线弧度α可以通过以下公式计算：
α=θ
其中，θ是曲线在某一点处与x轴的夹角。


需要注意的是，这些公式适用于平曲线的一般情况。

在实际应用中，根据具体的曲线类型和表示方式，可能需要对公式进行相应的调整。

曲线要素计算公式
曲线是数学中的基本概念，是指在平面上由无数个点连接而成的
连续曲线。

曲线具有许多重要的特征，如长度、弧度、曲率等。

而曲线的要素计算就是计算曲线的各种特征值。

下面，我们就来
介绍曲线要素的计算公式，帮助大家更深入地了解曲线的特征和性质。

一、曲线长度的计算公式：
曲线的长度指的是曲线上所有点之间的直线距离总和。

计算公式为：
L = ∫a b √[1+f’(x)²]dx
其中，a和b为曲线上的两个端点，f’(x)表示曲线的导数。

二、曲率的计算公式：
曲率是曲线某一点处曲线的弯曲程度的量度。

计算公式为：
k = |f’’(x)| / [1+f’(x)²]^(3/2)
其中，f’’(x)为曲线的二阶导数。

三、曲线斜率的计算公式：
曲线的斜率是指曲线在某一点处的切线斜率。

计算公式为：
f’(x) = lim Δx→0 [f(x+Δx)−f(x)] / Δx
四、曲线弧度的计算公式：
曲线的弧度是指曲线某一段的弧长对半径的比值。

计算公式为：θ = l / r
其中，l为曲线一段的弧长，r为曲线的半径。

以上就是曲线要素计算公式的详细介绍。

掌握这些公式可以涵盖曲线的多方面特征，并为实际问题的解决提供指导和依据。