曲线要素等计算公式表格

一、曲线要素计算已知：JDZH 、JDX 、JDY 、R 、L S1、L S2、L H 、T 、A 1、A 2（L H =L S1+L S2+圆曲线长）1、求ZH 点（或ZY 点）坐标及方位角⎪⎩⎪⎨⎧-=-=-=11sin cos AT JDY ZHY A T JDX ZHX TJDZH ZHZH 2、求HZ 点（或YZ 点）坐标及方位角⎪⎩⎪⎨⎧+=+=+-=22sin cos AT JDY HZY A T JDX HZX L T JDZH HZZH H3、求解切线长T 、外距E 、曲线长L（1）圆曲线⎪⎩⎪⎨⎧=-==180/)1)2/cos(/1()2/tan(απααR L R E R T （2）缓圆曲线 )2/(2/)2/cos(/)(2180/)21()2/tan()(020R l l l Rl l R p R E l R L qp R T s s s HsH H ===⎪⎩⎪⎨⎧-+=+⨯-=+⨯+=ββαπβα时当其中 二、直线上各桩号坐标及方位角计算 已知：ZH 、X 、Y 、A ⎪⎩⎪⎨⎧+=+==-=A L Y DY A L X DX A T ZH DZH L sin cos 三、第一缓和曲线上各桩号点坐标及方位角计算 已知：ZHZH 、ZHX 、ZHY 、A 1、R 、L S1、i （Z+1Y-1） ⎪⎩⎪⎨⎧⨯-+=⨯++=⨯⨯-==-=-=1111121132125cos sin sin cos /180)2/()6/()40/(Ay i A x ZHY DY A y i A x ZHX DX Rl l i A T Rl L y l R L L x ZHZH DZH L s s s π四、圆曲线上各桩号点坐标及方位角计算已知：ZHZH 、ZHX 、ZHY 、A 1、R 、L S1、i （Z+1Y-1）⎪⎩⎪⎨⎧⨯-+=⨯++=⨯+⨯-=⎪⎩⎪⎨⎧=-==++-=-++=--=1111121231110211231111cos sin sin cos /180)/2/(24/240/2/2/24/)]/2/cos(1[240/2/)/2/sin(Ay i A x ZHY DY A y i A x ZHX DX R L R l i A T R l p R l l q R l R l R L R l R y R l l R L R l R x ls ZHZH DZH L s s s s s s s s s s πβ其中五、第二缓和曲线上个桩号坐标及方位角计算 已知：HZZH 、HZX 、HZY 、A2、R 、L S2、i （Z+1Y-1） ⎪⎩⎪⎨⎧⨯--=⨯+-=⨯⨯+==-=-=2222222232225cos sin sin cos /180)2/()6/()40/(Ay i A x HZY DY A y i A x HZX DX Rl l i A T Rl L y l R L L x DZHHZZH L s s s π六、边桩坐标求解 已知：DZH 、X 、Y 、T 、BZJL （Z+Y-）、DLJJ 、N （距中桩距离，左正右负）⎪⎩⎪⎨⎧-=-=+=T N Y BDY T N X BDX T T sin cos α七、纵断面高程计算（1） 直线段上高程计算 已知：直线上任一点桩号（ZH ）、高程（H ）、纵坡（i ）)(*ZH DZH i H DH -+=（2） 竖曲线上高程计算已知：竖曲线起点桩号（ZH ）、起点高程（H ）、竖曲线半径R 、起点坡度（i ）、k （凸曲线+1、凹曲线-1） )2/(2R l k il H DH ZHDZH l ⨯-+=-=注：JDZH 、JDX 、JDY ：交点桩号、交点X 、Y 坐标R 、L S1、L S2：半径、缓和曲线1、缓和曲线2LH ：缓和曲线1长 +圆曲线长+ 缓和曲线2长 A1、A2：方位角1、方位角2 T ：在曲线要素中代表切线长；在坐标计算中代表被求解点的坐标方位角。

曲线道路坐标计算§1 曲线要素计算缓和曲线是在不改变直线段方向和保持圆曲线半径不变的条件下，插入到直线段和圆曲线之间的。

其曲率半径ρ从直线的曲率半径∞（无穷大）逐渐变化到圆曲线的半径R ，在缓和曲线上任意一点的曲率半径ρ与缓和曲线的长度l 成反比，以公式表示为：l1∝ρ 或 C l =⋅ρ（C 为常数，称曲线半径变更率）。

当o l l =时，R =ρ，应有o l R l C ⋅=⋅=ρ以上几式是缓和曲线必要的前提条件。

在实际应用中，可采取符合这一前提条件的曲线作为缓和曲线。

常用的有辐射螺旋线及三次抛物线，我国采用辐射螺旋线。

为了在圆曲线与直线之间加入一段缓和曲线o l ，原来的圆曲线需要在垂直于其切线的方向移动一段距离p ，因而圆心就由'O 移到O ，而原来的半径R 保持不变，如图。

由图中可看出，缓和曲线约有一半的长度是靠近原来的直线部分，而另一半是靠近原来的圆曲线部分，原来圆曲线的两端其圆心角o β相对应的那部分圆弧，现在由缓和曲线所代替，因而圆曲线只剩下缓圆点(HY )到圆缓点(YH )这段长度即y l 。

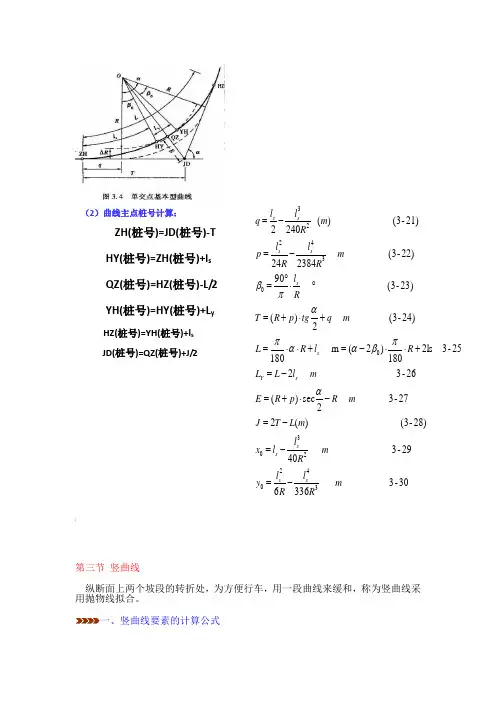
o β为缓和曲线的切线角，即缓圆点或圆缓点切线与直缓点或缓直点切线的交角，亦即圆曲线HY→YH 两端各延长2ol 部分所对应的圆心角。

γ为缓和曲线总偏角，即从直缓点(ZH )测设缓圆点(HY )或从缓直点(HZ )测设圆缓点(YH )的偏角。

q 为切线增量(切垂距)，即ZH (或HZ )到从圆心O 向ZH (或HZ )的切线作垂线垂足的距离。

p 为圆曲线内移值，即垂线(从圆心O 向ZH (或HZ )的切线作垂线)长与圆曲线半径R 之差。

§1.1 不等长缓和曲线要素计算：在铁路曲线测设中，线路曲线一般是由相等的两条缓和曲线中间加一个圆曲线构成，有时还会出现由两个不等长的缓和曲线中间加一个圆曲线构成的特殊情况，如图：缓和曲线长分别为1o l 、2o l ， 切线长分别为1T 、2T ，曲线偏角(线路转角)为α，圆曲线半径为R ，圆曲线长为y l ，曲线长为L ，外矢距为E ，切曲差为J ，(缓和曲线后)圆曲线内移值分别为1p 、2p ，(缓和曲线)切线增量分别为1q 、2q ，缓和曲线偏角分别为1o β、2o β ， 回旋线参数分别为121o Rl A =、222o Rl A =各曲线要素计算公式如下：231112402R ll q o o -=232222402Rll q o o -=341211268824R lR l p o o -=342222268824RlR l p o o -=ααsin )(2)(12111p p tgp R q T -+++=ααsin )(2)(21222p p tgp R q T -+++=Rl R l o o o ππβ111901802=⋅=Rl R l o o o ππβ222901802=⋅=︒--++=180)(2121Rl l L o o o o πββα从以上公式可以看出，当21o o l l =时，就是等长(对称)缓和曲线的情况。

：第三节 竖曲线纵断面上两个坡段的转折处，为方便行车，用一段曲线来缓和，称为竖曲线采用抛物线拟合。

一、竖曲线要素的计算公式（2）曲线主点桩号计算：ZH(桩号)=JD(桩号)-THY(桩号)=ZH(桩号)+l s QZ(桩号)=HZ(桩号)-L/2 YH(桩号)=HY(桩号)+L y HZ(桩号)=YH(桩号)+l sJD(桩号)=QZ(桩号)+J/230-3 336629-3 4028)-(3 )(227-3 2sec )(26-3 225-3 2ls 180)2(m 18024)-(3 2)(23)-(3 9022)-(3 23842421)-(3 )( 240234202300034223m Rl R l y m R l l x m L T J m R p R E m l L L R l R L m q tg p R T Rl m R l R l p m R l l q s s s s s Y s ss s s s -=-=-=-⋅+=-=+⋅⋅-=+⋅⋅=+⋅+=︒⋅︒=-=-=απβααπαπβ相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时，是凹曲线；ω为负，是凸曲线。

2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: （前提：ω很小）L=Rω#竖曲线切线长：T=L/2=Rω/2竖曲线上任一点竖距h：竖曲线外距：[例1]、某山岭区二级公路，变坡点桩号为K5+，标高为，变坡点桩号的地面高程为，i1=+5%，i2=-4%，竖曲线半径R=2000m。

试计算竖曲线诸要素以及桩号为K5+和K5+处的设计高程，BPD的设计高程与施工高。

解：1.计算竖曲线要素ω= |i2-i1|= | =，为凸型。

曲线长L=Rω=2000×=180m 切线长T=L/2=180/2=90m外距E=T2/2R=902/2×2000=$2.计算设计高程竖曲线起点桩号=（K5+）-90=K4+竖曲线起点高程=×=竖曲线终点桩号=（K5+）+90=K5+竖曲线终点高程=×=桩号K5+处：横距K5x 1=（K5+ ）-（K4+）=60m 竖距h 1=x 12/2R=602/2×2000= 切线高程=（90-60）×=[+60×=设计高程=桩号K5+处： 横距x 2=(K5+-(K5+=20m竖距h 2=x 22/2R=202/2×2000= 切线高程=（90-20）×=设计高程=横距x 2=(K5+-(K4+=160m 竖距h 2=x 22/2R=1602/2×2000= 切线高程=+160×= 设计高程=设计高程==BPD 施工高=设计高程-地面高程=，应为挖方。

缓和曲线、竖曲线、圆曲线、匝道（计算公式）一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”) 求：①线路匝道上点的坐标：xy②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x0。

一、路线转角、交点间距的计算（一）在地形图上量出路线起终点及各路线交点的坐标：QD 23810,27180、JD1 23996，26977 、JD 224684，26591、 JD3248480，25885、JD4 25350，25204 、ZD2606225783，（二）计算公式及方法设起点坐标为 QD X0,Y0，第 i 个交点坐标为 JD i X i ,Y i , i1,2,3,4, 则坐标增量 DX X i X i 1, DY Y i Y i 1交点间距 D(DX )22 DY象限角arctanDYDX方向角 A 是由象限角计算的：象限DX DY A象限DX DY A Ⅰ++AⅢ--A180o Ⅱ-+ A 180oⅣ+-A360o转角i A i Ai 11.QD与 JD1之间：坐标增量 DX X1X 0 =2396623810=186 0DY Y1Y026977271802030交点间距 D(DX )2DY 218622032275.33m象限角arctan DY arctan20347.502 oDX186方向角 A0360o360o47.502o312.498o 2.JD1与 JD 2之间：坐标增量 DX X 2X1=2468423966=688 0DY Y2Y126591269773860交点间距 D(DX )2268823862DY788.89 m象限角arctanDYarctan386 29.294 oDX688方向角 A 1 360o360o 29.294o 330.706o 转角 1 =A 1 A 0 330.706o 312.498o 18.208o3. JD 2 与JD 3之间：坐标增量 DXX 3 X 2 =24840 24684=156 0DYY 3 Y 2 25885 26591706 0交点间距 D(DX )221562 706 2DY723.03m象限角arctanDYarctan706 77.54oDX156方向角 A 2 360o360o 77.54o 282.46o转角 2 =A 2 A 1 282.46o 330.706o 48.246 o4. JD 3与 JD 4 之间：坐标增量 DXX 4 X 3 =25350 24840=510 0DY Y 4 Y 3 25204 25885681 0交点间距 D(DX )225102681 2DY850.8m象限角arctan DYarctan 51053.171oDX681方向角 A 3 360o360o 53.171o306.829o 转角 3 =A 3 A 2 306.829 282.4624.369o5. JD 4 与 ZD 之间：坐标增量 DXX X 4 =26062 25350=712 0DYYY 4 2578325204579 0交点间距 D (DX )2 27122 5792 917.706mDY象限角arctanDYarctan57939.118 oDX712方向角 A 039.118o转角 4 =A 4 A 3 39.118o 312.498o 92.289o二、各平曲线要素的计算( 一) JD 1曲线要素计算取R 800m ,设计速度为 60km/ h ,JD1桩号为K0+275.33，转角1.缓和曲线长度 L S，则：L SV 30.0366030.0369.72(m)R800L SV60350(m) 33.63.6L S R~ R800~ 80088.89 ~ 800(m) 99取整数，采用缓和曲线长120m（《公路工程技术标准》规定：V 最小缓和曲线长度为50m ）.2.圆曲线内移值 RL2S L4S120212040.75(m)R2688 (R)324 8002688 (800) 324R3.总切线长T hL S L3S120120359.989(m)先求 q240R2224080022所以 T h (R R) tan q(80018.20859.989 188.31(m)0.75) tan224.曲线总长度 L hL S=0.0752RL h ( 2 )R 2L S?R+L S 374.22(m)1801805.五个基本桩号JD 1K0+274.33)T h188.31ZH 1K 0+087.0218.208o60 km h 时，)L SHY1)( L h 2L S )YH1)L SHZ 11L h)2QZ1120.00K0+207.02134.22 K0+341.24120.00 K0+461.24187.11 K0+274.13E h ( R R)sec R (8000.75sec 18.208800 10.97(m)22超距 D2T L h 2 188.31374.22 2.4(m)。

曲线坐标计算一、圆曲线圆曲线要素：a -------------- 曲线转向角R -------------- 曲线半径根据a及R可以求出以下要素：T --------------- 切线长L -------------- 曲线长E -------------- 外矢距q -------------- 切曲差（两切线长与曲线全长之差）各要素的计算公式为:L R180（弧长）E RRsec 1）2（sec a =cos a 的倒数）圆曲线主点里程：ZY=J[> TQZ=ZY + L/2 或QZ=JD —q /2YZ=QZ + L/2 或YZ=JD + T—qJD=QZ + q/2 （校核用）1、基本知识里程：由线路起点算起，沿线路中线到该中线桩的距离。

表示方法：DK26＋284.56 。

“+”号前为公里数，即26km，“ +”后为米数，即284.56m CK ——表示初测导线的里程。

DK ——表示定测中线的里程。

K ——表示竣工后的连续里程。

铁路和公路计算方法略有不同。

2、曲线点坐标计算（偏角法或弦切角法）已知条件：起点、终点及各交点的坐标。

1）计算ZY、YZ 点坐标通用公式：2）计算曲线点坐标①计算坐标方位角i 点为曲线上任意一点li为i点与ZY点里程之差当曲线左转时用“-”，右转时用“ +”② 计算弦长③ 计算曲线点坐标此时的已知数据为：ZY ( xZY , yZY 、？ZY- i 、C 。

根据坐标正算原理：切线支距法 这种方法是以曲线起点ZY 或终点YZ 为坐标原点，以切线为X 轴，以过原点的半径为丫轴，则圆曲线上任意一点的切线支距坐标可通过以下公式求得： 利用坐标平移和旋转，该点在大地平面直角坐标系中的坐标可由以下公式求得: 式中：a 为ZY(YZ)点沿线路前进方向的切线方位角。

当起点为ZY 时“土”取“ + ”，XO=X(ZY),YO=Y(ZY),曲线为左偏时应以yi=-yi 代入；当起点为YZ 时，“土”取“ -”，XO=X(YZ), YO=Y(YZ), 曲线为左偏时应以yi 二yi 代入；弧长所对的圆心角弦切角弦的方位角注：1、同弧所对的圆周角等于圆心角的一半2、切线性质圆的切线与过切点的半径相垂直3、弦切角定理弦切角等于它所夹弧上的圆周角4、弧长公式由L/ n R=n /180 °得L=n°n R/ 180 °=n n R/180二、缓和曲线(回旋线)缓和曲线主要有以下几类：A:对称完整缓和曲线(基本形)------切线长、Is1与ls2都相等。

精心整理第三节竖曲线纵断面上两个坡段的转折处，为方便行车，用一段曲线来缓和，称为竖曲线采用抛物线拟合。

一、竖曲线要素的计算公式相邻坡段的坡度为i 1和i 2,代数差为ω=i 2-i 1ω为正时，是凹曲线；ω为负，是凸曲线。

2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R:（前提：ω很小）L=R ω竖曲线切线长：T=L/2=R ω/2竖曲线上任一点竖距h ：（2）曲线主点桩号计算：ZH(桩号)=JD(桩号)-THY(桩号)=ZH(桩号)+l sQZ(桩号)=HZ(桩号)-L/2YH(桩号)=HY(桩号)+L yHZ(桩号)=YH(桩号)+l sJD(桩号)=QZ(桩号)+J/230-3 336629-3 4028)-(3 )(227-3 2sec )(26-3 225-3 2ls 180)2(m 18024)-(3 2)(23)-(3 9022)-(3 23842421)-(3 )( 240234202300034223m Rl R l y m Rl l x m L T J m R p R E m l L L R l R L m q tg p R T R l m R l R l p m R l l q s s s s s Y s s s s s s -=-=-=-⋅+=-=+⋅⋅-=+⋅⋅=+⋅+=︒⋅︒=-=-=απβααπαπβ竖曲线外距：[例1]、某山岭区二级公路，变坡点桩号为K5+030.00，标高为427.68m，变坡点桩号的地面高程为450.65m，i1=+5%，i2=-4%，竖曲线半径R=2000m。

试计算竖曲线诸要素以及桩号为K5+000.00和K5+100.00处的设计高程，BPD 的设计高程与施工高。

解：1.计算竖曲线要素ω=|i2-i1|=|-0.04-0.05|=0.09，为凸型。

曲线长L=Rω=2000×0.09=180m切线长T=L/2=180/2=90m外距E=T2/2R=902/2×2000=2.03m2.计算设计高程竖曲线起点桩号=（K5+030.00）-90=K4+940.00竖曲线起点高程=427.68-90×0.05=423.18竖曲线终点桩号=（K5+030.00）+90=K5+120.00竖曲线终点高程=427.68-90×0.04=424.08桩号K5+000.00处：横距K5x1=（K5+000.00）-（K4+940.00）=60m竖距h1=x12/2R=602/2×2000=0.90m切线高程=427.68-（90-60）×0.05=426.18m423.18+60×0.05=426.18设计高程=426.18-0.90=425.28m桩号K5+100.00处：横距x2=(K5+120.00)-(K5+100.00)=20m竖距h2=x22/2R=202/2×2000=0.1m切线高程=427.68-（90-20）×0.04=424.88m设计高程=424.88-0.1=424.78m横距x2=(K5+100.00)-(K4+940.00)=160m竖距h2=x22/2R=1602/2×2000=6.4m切线高程=423.18+160×0.05=431.18m设计高程=431.18-6.40=424.78mBPD设计高程=427.68-E=425.65mBPD施工高=设计高程-地面高程=425.65-450.65=-25m，应为挖方。

[转]缓和曲线、竖曲线、圆曲线、匝道（计算公式）来源：王维超的日志一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：xy②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x0时sgn(x)=1，当x=0时sgn(。