一阶系统与二阶系统

标题一阶二阶系统的公式推导过程自控前两章的学习主要是打基础，到了第三章才真正开始了自控这门课的核心内容。

在前两章建立起系统模型后，接下来要进行的就是认识系统——即分析系统的性能指标，第三章介绍了三种方法中的第一种——时域分析法。

我们首先要明确本章讲了哪些内容。

时域方法是最基本的方法，也是我们在分析时最先想到的方法，它可以直接提供系统时间响应内的所有内容，直观且明确，但是也有它的缺点，那就是这一方法必须要基于求解系统输出的解析法，过程很是繁琐，这一局限性也就决定了应用时域法进行分析的系统阶数不能太高，所以本章我们研究对象只有一阶系统和二阶系统，其中二阶系统是研究的重点。

接下来分别给出一阶系统和二阶系统典型结构和其性能指标的定义，对系统输入典型输入信号，研究对应响应的情况，在这其中，最重点的是二阶系统的阶跃响应，其余的响应仅作了解即可。

注意到性能指标只能定量的描述一个系统响应的情况，考虑前面所提到的对于一个系统的基本要求：“稳、准、快”。

其中“快”——动态性能；“稳”——基本要求；“准”——稳态要求，往后的内容都是围绕这三个字。

对于“快”，其实就是系统的性能指标，对于“稳”，时域法介绍了赫尔维玆判据和劳斯判据，对于“准”，介绍了稳态误差还有校正方法。

以上就是本章的知识结构，接下来我们来一一介绍。

NO.1一阶系统我们从最简单的一阶系统说起，以下是一阶系统的典型结构：一阶系统中，只有特征参数：时间常数T。

虽然有五个典型输入信号，但一般我们只研究阶跃输入对应的响应，我们把阶跃信号称为“标准输入”，其单位阶跃响应曲线如下：对于一阶系统，对应的性能指标有两个：上升时间和调节时间。

1.上升时间从终值的10%上升到终值的90%所用的时间。

（此定义式基于非振荡的动态过程，要区别于后续的振荡动态过程）。

在一阶系统单位阶跃曲线上表示如下：2.调节时间指第一次进入误差带且信号以后都不出误差带的时间。

在响应曲线上表示为：注意:如上图，调节时间不是到A点的时间，因为曲线在A点以后还有出了误差带的部分。

一二阶系统频率特性测试与分析一、引言二阶系统是控制系统中常见的一种类型，它的频率特性对系统的稳定性和性能具有重要影响。

频率特性测试是分析系统动态响应的重要手段之一，通过对二阶系统进行频率特性测试和分析，可以获取系统的幅频特性和相频特性，进一步了解系统的稳定性和性能指标。

本文将介绍二阶系统频率特性测试的基本原理和方法，并通过实例进行分析。

二、二阶系统频率特性测试原理二阶系统是由两个一阶系统级联组成的复合系统，其传递函数可以表示为：G(s)=K/((s+a)(s+b))其中K为系统的增益，a和b为系统的两个极点。

二阶系统的频率特性可以通过系统的幅频特性和相频特性来描述。

1.幅频特性：幅频特性反映了系统对不同频率输入信号的增益响应。

在频率特性测试中，可以通过给系统输入正弦信号，并测量系统输出信号的幅值与输入信号的幅值之比来得到系统的幅频特性。

一般情况下，可以使用频率响应仪或示波器进行测量。

2.相频特性：相频特性反映了系统对不同频率输入信号的相位响应。

在频率特性测试中，可以通过测量系统输出信号与输入信号的相位差来得到系统的相频特性。

一般情况下，可以使用频率响应仪或示波器进行测量。

三、二阶系统频率特性测试方法二阶系统的频率特性测试方法主要有两种，一种是激励法，另一种是响应法。

1.激励法：激励法是通过给系统输入不同频率的正弦信号，并测量系统的输出响应来获取系统的频率特性。

具体步骤如下：（1）设置输入信号的幅值和频率范围；（2）给系统输入不同频率的正弦信号，并记录系统的输出响应；（3）根据记录的数据，绘制系统的幅频特性曲线和相频特性曲线。

2.响应法：响应法是通过给系统输入一个周期或多个周期的脉冲信号，并测量系统的输出响应的特性来获取系统的频率特性。

具体步骤如下：（1）设置输入信号的幅值、频率和脉冲宽度；（2）给系统输入一个周期或多个周期的脉冲信号，并记录系统的输出响应；（3）根据记录的数据，绘制系统的幅频特性曲线和相频特性曲线。

实验名称：一二阶系统的电子模拟及时域响应测试课程名称：自动控制原理实验目录（一）实验目的 (3)（二）实验内容 (3)（三）实验设备 (3)（四）实验原理 (3)（五）一阶系统实验结果 (3)（六）一阶系统实验数据记录及分析 (7)（七）二阶系统实验结果记录 (8)（八）二阶系统实验数据记录及分析 (11)（九）实验总结及感想............................................................................错误!未定义书签。

图片目录图片1 一阶模拟运算电路 (3)图片2 二阶模拟运算电路 (3)图片3 T=0.25仿真图形 (4)图片4 T=0.25测试图形 (4)图片5 T=0.5仿真图形 (5)图片6 T=0.5测试图形 (5)图片7 T=1仿真图形 (6)图片8 T=1测试图形 (6)图片9 ζ=0.25s仿真图形 (8)图片10 ζ=0.25s测试图形 (8)图片11 ζ=0.5s仿真图形 (9)图片12 ζ=0.5s测试图形 (9)图片13 ζ=0.8s仿真图形 (10)图片14 ζ=0.8s测试图形 (10)图片15 ζ=1s仿真图形 (11)图片16 ζ=1s测试图形 (11)表格目录表格1 一阶系统实验结果 (7)表格2 二阶系统实验结果 (11)一二阶系统的电子模拟及时域响应测试（一）实验目的1.了解一、二阶系统阶跃响应及其性能指标与系统参数之间的关系。

2.学习在电子模拟机上建立典型环节系统模型的方法。

3.学习阶跃响应的测试方法。

（二）实验内容1.建立一阶系统的电子模型,观测并记录在不同时间常数T时的跃响应曲线,并测定其过渡过程时间TS。

2.建立二阶系统的电子模型,观测并记录在不同阻尼比ζ时的跃响应曲线,并测定其超调量σ%及过渡过程时间TS。

（三）实验设备HHMN电子模拟机，实验用电脑，数字万用表（四）实验原理一阶系统：在实验中取不同的时间常数T，由模拟运算电路，可得到不同时间常数下阶跃响应曲线及不同的过渡时间。

控制系统的时域分析_一二阶时间响应讲述时域分析是控制系统理论中的重要内容，主要用于分析系统的时间响应。

在时域分析中，我们会关注系统的输入和输出之间的关系，并研究系统在时间上的性能指标和特征。

本文将重点讲述一阶和二阶系统的时间响应。

一、一阶系统的时间响应一阶系统是指系统的传递函数中只有一个一阶多项式的系统，其传递函数形式为：G(s)=K/(Ts+1)其中，K是系统的增益，T是系统的时间常数。

一阶系统的单位阶跃响应是常用的时间响应之一，通过对系统施加一个单位阶跃输入，可以得到系统的响应曲线。

单位阶跃输入可以表示为：u(t)=1由于一阶系统的传递函数是一个一阶多项式，因此它的拉普拉斯变换可以通过部分分式展开得到：G(s)=K/(Ts+1)=A/(s+1/T)通过进行拉普拉斯逆变换，可以得到系统的单位阶跃响应函数y(t)：y(t) = K(1 - exp(-t/T))其中，exp(-t/T)为底数为e的指数函数，表示系统的响应曲线在t时刻的衰减程度。

从单位阶跃响应函数可以看出，一阶系统的时间常数T决定了系统的响应速度和衰减程度。

时间常数越小，系统的响应越快速，衰减程度也越快。

二、二阶系统的时间响应二阶系统是指系统的传递函数中有一个二阶多项式的系统，通常可以表示为：G(s) = K / (s^2 + 2ξω_ns+ω_n^2)其中，K是系统的增益，ξ是系统的阻尼比，ω_n是系统的自然频率。

二阶系统的时间常数和质量阻尼比是描述系统性能的重要参数。

时间常数决定了系统响应的速度，质量阻尼比则影响了系统的稳定性和衰减程度。

对于二阶系统的单位阶跃响应，可以通过拉普拉斯逆变换得到响应函数y(t)：y(t) = K*(1 - (1-ξ^2)^0.5 * exp(-ξω_nt) * cos((1-ξ^2)^0.5 * ω_nt + φ))其中，φ为相位角，由初始条件和变量确定。

从单位阶跃响应函数可以看出，二阶系统的阻尼比ξ决定了系统的过阻尼、临界阻尼和欠阻尼的响应形式。

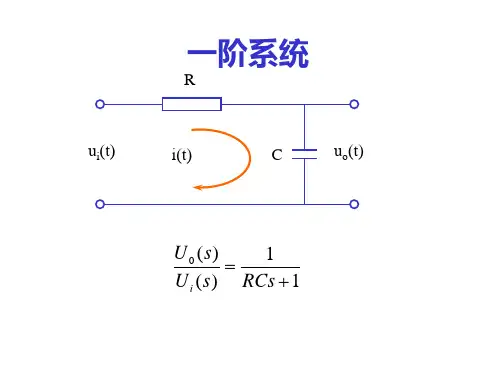
一阶二阶系统的动态响应1汇总一阶系统和二阶系统是控制系统中常见的两种动态响应模型。

它们在自然科学、工程技术等领域中具有重要的应用价值。

本文将对一阶系统和二阶系统的动态响应进行详细的介绍和分析，并对其特性进行总结和比较。

一、一阶系统的动态响应一阶系统是指系统的微分方程中只含有一阶导数的控制系统。

一阶系统的动态响应通常由一阶微分方程表示。

一般而言，一阶系统的微分方程可以表示为：$ \frac{dy(t)}{dt} = -ay(t) + bx(t) $其中，$y(t)$表示系统的输出，$x(t)$表示系统的输入，$a$和$b$为系统的参数。

根据方程的特性，可以推导出一阶系统的动态响应的数学表达式。

1.1零输入响应当系统处于零输入状态（即$x(t)=0$）时，系统的输出仅由初始条件决定。

一阶系统的零输入响应表达式为：$ y(t) = y(0)e^{-at} $其中，$y(0)$表示系统初始时刻的输出。

可以看出，在没有输入信号的情况下，一阶系统的输出会随着时间的推移而指数级衰减。

1.2零状态响应当系统处于零状态（即初始条件$y(0)$为0）时，系统的输出完全由输入信号决定。

一阶系统的零状态响应表达式为：$ y(t) = \frac{b}{a}(1 - e^{-at})x(t) $其中，$x(t)$表示系统的输入。

可以看出，在没有初始条件的情况下，一阶系统的输出将随着时间的推移而趋近于输入信号。

1.3一阶系统的阶跃响应阶跃响应是指当输入信号为单位阶跃函数时，系统的输出响应。

一阶系统的阶跃响应表达式为：$ y(t) = b(1 - e^{-at})\cdot u(t) $其中，$u(t)$表示单位阶跃函数。

可以看出，在单位阶跃输入信号的作用下，一阶系统的输出会随时间的推移而逐渐趋近于输入信号的幅值。

二、二阶系统的动态响应二阶系统是指系统的微分方程中含有二阶导数的控制系统。

二阶系统的动态响应通常由二阶微分方程表示。

快速性分析一阶二阶系统响应一阶和二阶系统是控制系统中常见的两种类型。

了解和分析这两种系统的响应特性对于掌握控制工程非常重要。

下面将从理论和实际角度分别讨论一阶和二阶系统的快速性分析。

一、一阶系统响应分析一阶系统是指具有一个可控参数的一阶微分方程。

常见的一阶系统包括RC电路和RL电路。

其方程形式为：τdy(t)/dt + y(t) = Ku(t)其中，τ是系统的时间常数，K是系统的增益，u(t)是输入信号，y(t)是输出信号。

1.理论分析一阶系统的理论响应可通过对微分方程进行求解来得到。

假设输入信号u(t)为单位阶跃函数，即：u(t)=1,t≥0;u(t)=0,t<0此时，微分方程的解为：y(t)=1-e^(-t/τ)根据解析解，可以得到一阶系统的重要性能指标：a) 上升时间（Rise Time）：定义为系统输出从0.1到0.9之间所需的时间。

对于一阶系统，上升时间可以近似为：Tr≈2.2τb) 峰值时间（Peak Time）：定义为系统输出达到峰值的时间。

Tp≈3τc) 超调量（Overshoot）：指系统输出超过其稳态值的最大量。

OS≈(e^(-π/(√(1-ζ^2)))-1)×100%其中，ζ是系统的阻尼比，对于一阶系统，ζ仅能取0，因此一阶系统不存在超调量。

d) 调节时间（Settling Time）：定义为系统输出在误差范围内稳定的时间。

Ts≈4τ2.实际分析除了理论分析，我们还可以通过实验或仿真来评估一阶系统的快速性能。

以下是一些实际分析的步骤：a)根据系统的特性指标选择适当的输入信号，例如单位阶跃、正弦波等。

b)将选定的输入信号施加到系统上，并记录系统的输出响应。

c)根据实际记录的数据，计算系统的性能指标，如上升时间、峰值时间等。

二、二阶系统响应分析二阶系统是具有二阶微分方程的系统，常见的例子包括机械振动系统、电路振荡器等。

其方程形式为：τ^2d^2y(t)/dt^2 + 2ζτdy(t)/dt + y(t) = Ku(t)其中，τ是系统的时间常数，ζ是系统的阻尼比，K是系统的增益，u(t)是输入信号，y(t)是输出信号。

一阶和二阶系统的数学模型如果知道测量系统的数学模型，经过适当的运算，通常都可以推算得到该测量系统对任何输入的动态输出响应。

但是测量系统的数学模型中的具体参数确定通常需经实验测定，亦称动态标定。

工程上常用阶跃和正弦两种形式的信号作为标定信号。

阶跃输入信号的函数表达式为式中，A为阶跃输入信号幅值。

采用阶跃输入信号具有适用性广、实施简单、易于操作等特点。

采用正弦输入信号对分析测量系统频率特性十分方便，但在对压力、流量、温度、物位等检测系统的实际应用中一般难以碰到被测参量以正弦方式变化的情况，可把被测参量随时间变化看作是在不同时刻一系列阶跃输入的叠加。

工程上常见的各类检测系统的动态响应特性大都与理想的一阶或二阶系统相近，少数复杂系统也可近似地看作两个或多个二阶系统的串并联。

1.一阶系统的标准微分方程不管是电学、力学，还是热工测量系统，其一阶系统的运动微分方程最终都可化成如下通式（1）式中，Y（t）为测量系统的输出函数；x（t）为测量系统的输入函数；为测量系统的时间常数；k为测量系统的放大倍数。

上述一阶系统的传递函数表达式为（2）上述一阶系统的频率特性表达式为（3）其幅频特性表达式为（4）其相频特性表达式为（5）2.二阶系统的标准微分方程不管是电学、力学或热工测量系统，其二阶系统的运动微分方程最终都可化成如下通式（6）式中，为二阶系统的固有角频率；为二阶系统的阻尼比；K为二阶系统的放大倍数或称系统静态灵敏度。

上述二阶系统的传递函数表达式为（7）上述二阶系统的频率特性表达式为（8）其幅频特性表达式为（9）其相频特性表达式为（10）下面着重介绍一阶和二阶系统的动态特性参数。

一阶系统和二阶系统区分方法-回复一阶系统和二阶系统是控制系统理论中常见的两种类型。

在实际应用中，了解如何区分这两种系统对于系统分析和设计具有重要意义。

本文将从数学模型的形式、特征方程的阶数、单位阶跃响应以及系统动态响应等方面逐步回答如何区分一阶系统和二阶系统。

一、数学模型的形式：一阶系统的数学模型通常可以写作以下形式：G(s) = \frac{K}{Ts + 1}其中，G(s)代表系统的传输函数，K为系统的增益，T为系统的时间常数。

二阶系统的数学模型通常可以写作以下形式之一：1. 标准二阶的形式：G(s) = \frac{K}{(T_1s + 1)(T_2s + 1)}其中，K为系统的增益，T_1和T_2分别为系统的两个时间常数。

2. 通用二阶的形式：G(s) = \frac{K\omega_n^2}{s^2 + 2\zeta\omega_ns +\omega_n^2}其中，K为系统的增益，\omega_n为系统的自然频率，\zeta为系统的阻尼比。

根据数学模型的形式，我们可以初步区分一阶系统和二阶系统。

二、特征方程的阶数：特征方程是描述系统响应的方程，其阶数等于系统的阶数。

对于一阶系统，特征方程的阶数为一，通常为一次多项式。

对于二阶系统，特征方程的阶数为二，通常为二次多项式。

通过观察特征方程的阶数，我们进一步可以区分一阶系统和二阶系统。

三、单位阶跃响应：单位阶跃响应是指当系统输入信号为单位阶跃函数时，系统的输出响应。

根据单位阶跃响应的形式，我们也可以区分一阶系统和二阶系统。

一阶系统的单位阶跃响应通常具有指数衰减的形式，即在初始时刻系统响应迅速达到稳定，并以指数形式趋于稳定值。

而对于二阶系统的单位阶跃响应，其形式通常包含了振荡（正弦项）和指数衰减（指数项）两部分。

其中，振荡部分描述了系统的振荡行为，而指数衰减部分描述了系统的稳态响应。

通过分析单位阶跃响应的形式，我们可以进一步确认一阶系统和二阶系统的类型。