3第三章热力学第二定律

第三章热力学第二定律热力学第一定律过程的能量守恒热力学第二定律过程的方向和限度§3.1 热力学第二定律（1）过程的方向和限度自发过程：体系在没有外力作用下自动发生的变化过程，其有方向和限度。

例如：水位差、温度差、压力差等引起的变化过程。

自发过程，有做功能力方向：始态终态反自发过程，需消耗外力平衡状态限度：始态终态无做功能力自发过程的共同特征：不可逆性（2）热力学第二定律的表达式经典表述：人们不能制造一种机器（第二类永动机），这种机器能循环不断地工作，它仅仅从单一热源吸取热量均变为功，而没有任何其它变化。

一般表述：第二类永动机不能实现。

§3.2 卡诺循环1824年，法国工程师卡诺（Carnot）使一个理想热机在两个热源之间，通过一个特殊的可逆循环完成了热→功转换，给出了热机效率表达式。

这个循环称卡诺循环。

（1）卡诺循环过程设热源温度T1 > T2，工作物质为理想气体。

卡诺循环1. 恒温可逆膨胀（A → B ）：0U 1=∆ 12111V V lnnRT W Q == 2. 绝热可逆膨胀（B → C ）：0q =， )T T (nC U W 21V 22-=∆-=3. 恒温可逆压缩（C → D ）：0U 3=∆， 342322V V lnnRT W q Q ==-= 4. 绝热可逆压缩（D → A ）：0q =， )T T (nC U W 12V 44-=∆-=整个循环过程的总功为：34212112V 34221V 1214321V Vln nRT V V lnnRT )T T (nC V Vln nRT )T T (nC V V ln nRT W W W W W +=-++-+=+++= 热机循环一周有：0U =∆， W q Q Q Q Q 2121=-=+=热机效率：1213421211V V ln nRT V Vln nRT V V lnnRT Q W+==η对于绝热可逆膨胀：k12312V V T T -⎪⎪⎭⎫ ⎝⎛=对于绝热可逆压缩： k14121V V T T-⎪⎪⎭⎫ ⎝⎛=比较得：1423V V V V =或 4312V V V V = 则： 121121Q Q Q T T T +=-=η η— 卡诺热机效率（2） 卡诺定理卡诺定理：一切工作于高温热源T 1与低温热源T 2之间的热机效率，以可逆热机的效率为最大。

第三章 热力学第二定律 本章知识要点与公式1.自发变化的不可逆性；一个自发变化发生后，不可能使系统和环境都恢复到原来的状态而不留下任何影响，自发变化具有方向性，是不可逆的。

2.热力学第二定律Clausius ：不可能把热从低温物体传到高温物体，而不引起其他变化。

Kelvin ：不可能从单一热源取出热使之完全变为功，而不发生其他的变化。

热力学第二定律表明：热转化为功是有条件的，有限度的，而功转化为热是无条件的。

3.Carnot 定律所有工作于同温热源与同温冷源之间的热机，其效率不可能超过可逆热机；所有工作于同温热源与同温冷源之间的可逆热机，其热机效率都相等。

4.熵（1）熵的数学表达式2pG H T T T ⎛∆⎫⎛⎫∂ ⎪ ⎪∆⎝⎭ ⎪=-∂ ⎪ ⎪⎝⎭B A R Q S T δ⎛⎫∆= ⎪⎝⎭⎰或Rδd Q S T ⎛⎫= ⎪⎝⎭ （2）Clausius 不等式d d 0Q S T =≥或d d QS T≥ 可利用不等式来判别过程的可逆性；等式表示可逆过程，不等式表示不可逆过程。

（3）熵增加原理在绝热过程中，若过程是可逆的则系统的熵是不变的，若过程是不可逆的，则系统的熵增加，绝热不可逆过程当达到平衡时，熵达到最大值。

5.熵的计算等温过程中熵的变化值（1） 理想气体等温可逆变化max R 2112ln ln W Q V pS nR nR T T V p -∆====（2） 等温等压可逆变化()()()H S T ∆∆=相变相变相变（3） 理想气体的等温等压混合过程，且符合分体积定律，mix B B Bln S R n x ∆=-∑非等温过程熵的变化值。

（4） 可逆等容，变温过程21,m d T V T nC S T T ∆=⎰ （5） 可逆等压，变温过程21,m d T p T nC S T T∆=⎰（6） 分布计算法12211221T ,m 212T 1T ,m 112T 2ln d ln d S S V S S p A C B nC V S S S nR T V T A C B nC p S S S nR T p T ∆∆''∆∆⎧⎫−−−−→−−−−→⎪⎪⎪⎪∆=∆+∆=+⎪⎪⎪⎪⎨⎬−−−−→−−−−→⎪⎪⎪⎪⎪⎪∆=∆+∆=+⎪⎪⎩⎭⎰⎰等温可逆等容可逆等温可逆等压可逆5.热力学第二定律本质：在隔离系统中，由比较有次序的状态向比较无次序的状态变化，是自发变化的方向。

第三章 热力学第二定律一．基本要求1．了解自发变化的共同特征，熟悉热力学第二定律的文字和数学表述方式。

2．掌握Carnot 循环中，各步骤的功和热的计算，了解如何从Carnot 循环引出熵这个状态函数。

3．理解Clausius 不等式和熵增加原理的重要性，会熟练计算一些常见过程如：等温、等压、等容和,,p V T 都改变过程的熵变，学会将一些简单的不可逆过程设计成始、终态相同的可逆过程。

4．了解熵的本质和热力学第三定律的意义，会使用标准摩尔熵值来计算化学变化的熵变。

5．理解为什么要定义Helmholtz 自由能和Gibbs 自由能，这两个新函数有什么用处？熟练掌握一些简单过程的,,H S A ΔΔΔ和G Δ的计算。

6．掌握常用的三个热力学判据的使用条件，熟练使用热力学数据表来计算化学变化的，和r m H Δr m S Δr m G Δ，理解如何利用熵判据和Gibbs 自由能判据来判断变化的方向和限度。

7．了解热力学的四个基本公式的由来，记住每个热力学函数的特征变量，会利用d 的表示式计算温度和压力对Gibbs 自由能的影响。

G 二．把握学习要点的建议自发过程的共同特征是不可逆性，是单向的。

自发过程一旦发生，就不需要环境帮助，可以自己进行，并能对环境做功。

但是，热力学判据只提供自发变化的趋势，如何将这个趋势变为现实，还需要提供必要的条件。

例如，处于高山上的水有自发向低处流的趋势，但是如果有一个大坝拦住，它还是流不下来。

不过，一旦将大坝的闸门打开，水就会自动一泻千里，人们可以利用这个能量来发电。

又如，氢气和氧气反应生成水是个自发过程，但是，将氢气和氧气封在一个试管内是看不到有水生成的，不过，一旦有一个火星，氢气和氧气的混合物可以在瞬间化合生成水，人们可以利用这个自发反应得到热能或电能。

自发过程不是不能逆向进行，只是它自己不会自动逆向进行，要它逆向进行，环境必须对它做功。

例如，用水泵可以将水从低处打到高处，用电可以将水分解成氢气和氧气。

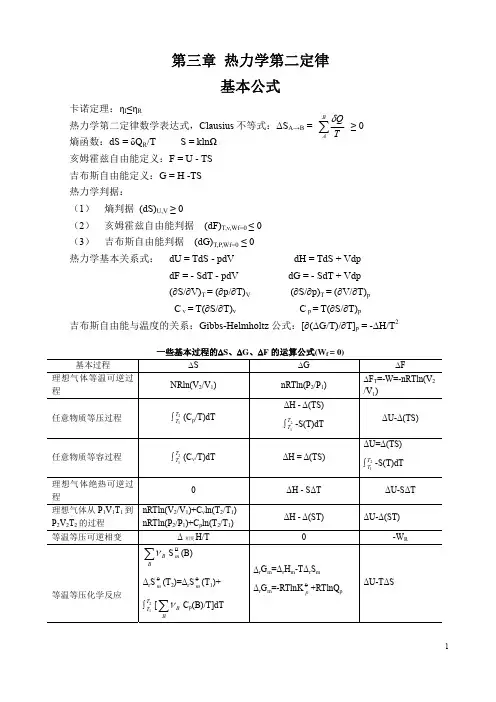
第三章热力学第二定律基本公式卡诺定理：ηI≤ηR热力学第二定律数学表达式，Clausius不等式：ΔS A→B = ∑BATQδ≥ 0熵函数：dS = δQ R/T S = klnΩ亥姆霍兹自由能定义：F = U - TS吉布斯自由能定义：G = H -TS热力学判据：（1） 熵判据 (dS)U,V≥ 0（2） 亥姆霍兹自由能判据(dF)T,v,Wf=0 ≤ 0（3） 吉布斯自由能判据(dG)T,P,Wf=0≤ 0热力学基本关系式：dU = TdS - pdV dH = TdS + VdpdF = - SdT - pdV dG = - SdT + Vdp(∂S/∂V)T = (∂p/∂T)V(∂S/∂p)T = (∂V/∂T)pC v = T(∂S/∂T)v C p = T(∂S/∂T)p吉布斯自由能与温度的关系：Gibbs-Helmholtz公式：[∂(ΔG/T)/∂T]p = -ΔH/T2一些基本过程的ΔS、ΔG、ΔF的运算公式(W例题例1 一个理想卡诺热机在温差为100K的两个热源之间工作，若热机效率为25％，计算T1、T2和功，已知每一循环中T1热源吸热1000J，假定所作的功W以摩擦热的形式完全消失在T2热源上，求该热机每一循环后熵变和环境的熵变。

解：卡诺热机效率η = (T2 - T1)/T225% =100K/T2, T2=400K, T1 = 300K热机效率定义：η = W/Q2η = W/(Q1+ W), 25% =W/(1000J + W), W =333.3JQ2 = W/η = 333.3J/25% = 1333JΔS体 =0(热机循环一周回到原态)由题意知，热机对环境所作的功完全以摩擦热的形式释放在T2热源上。

故T2热源得到了W的热量。

放出了Q2的热量。

ΔS环 =Q环,1/T1 + Q环,2/T2 = Q1/T1 + (Q2+W)/T2=1000J/300K + (-1333+333.3)J/400K =0.83J.K -1例2 有一绝热体系，中间隔板为导热壁，右边容积为左边容积的2倍，已知气体的C V,m = 28.03 J.mol-1，试求：1mol O2 273K 2mol N2 298K(a)不抽掉隔板达平衡后的ΔS ；(b) 抽去隔板达平衡后的ΔS。

第三章热力学第二定律第三章 热力学第二定律（一）主要公式及其适用条件1、热机效率1211211/)(/)(/T T T Q Q Q Q W -=+=-=η式中：Q 1及Q 2分别为工质在循环过程中从高温热源T 1所吸收的热量和向低温热源T 2所放出的热量，W 为在循环过程中热机对环境所作的功。

此式适用于在两个不同温度的热源之间所进行的一切可逆循环。

2、卡诺定理的重要结论⎩⎨⎧<=+不可逆循环可逆循环,0,0//2211T Q T Q不论是何种工作物质以及在循环过程中发生何种变化，在指定的高、低温热源之间，一切要逆循环的热温商之和必等于零，一切不可逆循环的热温商之和必小于零。

3、熵的定义式TQ dS /d r def ＝ 式中：r d Q 为可逆热，T 为可逆传热r d Q 时系统的温度。

此式适用于一切可逆过程熵变的计算。

4、克劳修斯不等式⎰⎩⎨⎧≥∆21)/d (可逆过程不可逆过程T Q S上式表明，可逆过程热温商的总和等于熵变，而不可逆过程热温商的总和必小于过程的熵变。

5、熵判据∆S (隔) = ∆S (系统) + ∆S (环境)⎩⎨⎧=>系统处于平衡态可逆过程能自动进行不可逆,,0,,0 此式适用于隔离系统。

只有隔离系统的总熵变才可人微言轻过程自动进行与平衡的判据。

在隔离系统一切可能自动进行的过程必然是向着熵增大的方向进行，绝不可能发生∆S （隔）<0的过程，这又被称为熵增原理。

6、熵变计算的主要公式⎰⎰⎰-=+==∆212121r d d d d d T p V H T V p U T Q S对于封闭系统，一切可逆过程的熵变计算式，皆可由上式导出。

（1）∆S = nC V ,m ln(T 2/T 1) + nR ln(V 2/V 1)= nC p,m ln(T 2/T 1) + nR ln(p 2/p 1)= nC V ,m ln(p 2/p 1) + nC p,m ln(V 2/V 1)上式适用于封闭系统、理想气体、C V ,m =常数、只有pVT 变化的一切过程。

第三章 热力学第二定律主要公式及使用条件1. 热机效率1211211/)(/)(/T T T Q Q Q Q W -=+=-=η式中1Q 和2Q 分别为工质在循环过程中从高温热源T 1吸收的热量和向低温热源T 2放出的热。

W 为在循环过程中热机中的工质对环境所作的功。

此式适用于在任意两个不同温度的热源之间一切可逆循环过程。

2. 卡诺定理的重要结论2211//T Q T Q +⎩⎨⎧=<可逆循环不可逆循环,,00任意可逆循环的热温商之和为零，不可逆循环的热温商之和必小于零。

3. 熵的定义4. 克劳修斯不等式d S {//Q T Q T =>δ, δ, 可逆不可逆5. 熵判据a mb s y s i s o S S S ∆+∆=∆{0, 0, >=不可逆可逆 式中iso, sys 和amb 分别代表隔离系统、系统和环境。

在隔离系统中，不可逆过程即自发过程。

可逆，即系统内部及系统与环境之间皆处于平衡态。

在隔离系统中，一切自动进行的过程，都是向熵增大的方向进行，这称之为熵增原理。

此式只适用于隔离系统。

6. 环境的熵变rd δ/S Q T =ambys amb amb amb //S T Q T Q s -==∆7. 熵变计算的主要公式222r 111δd d d d Q U p V H V p S T T T+-∆===⎰⎰⎰ 对于封闭系统，一切0=W δ的可逆过程的S ∆计算式，皆可由上式导出（1）,m 2121ln(/)ln(/)V S nC T T nR V V ∆=+,m 2112ln(/)ln(/)p S nC T T nR p p ∆=+,m 21,m 21ln(/)ln(/)V p S nC p p nC V V ∆=+上式只适用于封闭系统、理想气体、,m V C 为常数，只有pVT 变化的一切过程（2） T 2112l n (/)l n (/)S n R V V n R p p ∆=＝ 此式使用于n 一定、理想气体、恒温过程或始末态温度相等的过程。