一次函数的图像(1)

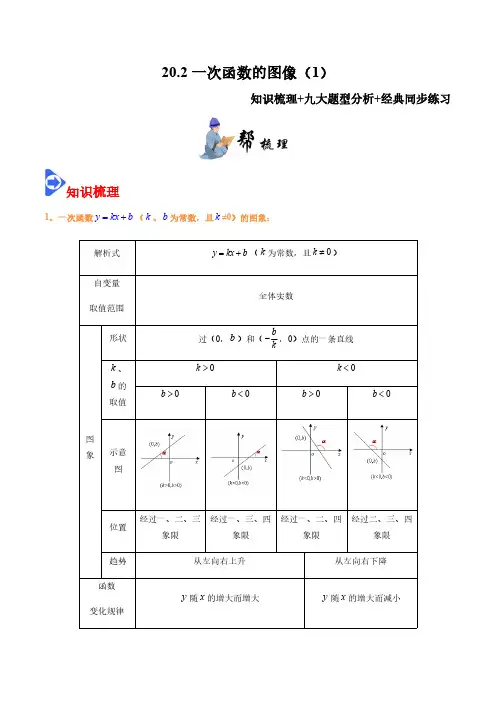
20.2一次函数的图像（1）知识梳理+九大题型分析+经典同步练习知识梳理1、一次函数（、为常数，且≠0）的图象：解析式（为常数，且）自变量取值范围全体实数形状过（0，）和（，0）点的一条直线、的取值示意图位置经过一、二、三象限经过一、三、四象限经过一、二、四象限经过二、三、四象限图象趋势从左向右上升从左向右下降函数变化规律随的增大而增大随的增大而减小y kx b =+k b k y kx b =+k 0k ¹b bk-k >0k <k b 0b >0b <0b >0b <y x y x2、 、对一次函数的图象和性质的影响：①一条直线与轴的交点的纵坐标叫做这条直线在轴上的截距，直线的截距是.②由于值的不同，则直线相对于轴正方向的倾斜程度不同，这个常数称为直线的斜率.③决定直线从左向右的趋势，决定它与轴交点的位置，、一起决定直线经过的象限．3、函数（、为常数，且≠0）的图象是一条直线 ：①当＞0时，直线是由直线向上平移个单位长度得到的；②当＜0时，直线是由直线向下平移||个单位长度得到的.4.、两条直线：和：的位置关系可由其系数确定：①与相交； ②，且与平行；典型例题题型一：由k ，b 的符号判断一次函数图像例题1一次函数y ＝－3x －2的图象不经过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】A 【解析】根据一次函数的性质，当k ＜0，b ＜0时，图象经过第二、三、四象限解答．解：∵k=-3＜0，∴函数经过第二、四象限，k b y kx b =+y y y kx b =+b k x k k y kx b =+b y k b y kx b =+y kx b =+k b k b y kx b =+y kx =b b y kx b =+y kx =b 1l 11y k x b =+2l 22y k x b =+12k k ¹Û1l 2l 12k k =12b b ¹Û1l 2l∵b=﹣2＜0，∴函数与y 轴负半轴相交，∴图象不经过第一象限．故选A题型二：利用一次函数的图像判断k ，b 的符号例题2已知一次函数y kx b =+的图象如图所示，则k ，b 的符号是（ ）A ．0k >，0b >B ．0k >，0b <C ．k 0<，0b >D ．k 0<，0b <【答案】D 【解析】由图可知，一次函数y=kx+b 的图象经过二、三、四象限，根据一次函数图象在坐标平面内的位置与k 、b 的关系作答．解：由一次函数y ＝kx+b 的图象经过二、三、四象限，又有k ＜0时，直线必经过二、四象限，故知k ＜0，再由图象过三、四象限，即直线与y 轴负半轴相交，所以b ＜0．故答案为：D ．题型三：k ，b 的符号与一次函数图像的综合问题例题3若关于x 的一元二次方程x 2﹣2x+kb+1＝0没有实数根，则一次函数y ＝kx+b 的大致图象可能是（ ）A ．B ．C ．D ．【答案】A 【解析】由根的判别式△＜0，即可得出k 、b 同号，再利用一次函数图象与系数的关系找出k ＞0、b ＞0或k ＜0、b ＜0时，一次函数y ＝kx+b 的图象经过的象限，此题得解．解：∵关于x 的一元二次方程x 2﹣2x+kb+1＝0没有实数根，∴△＝（﹣2）2﹣4×1×（kb+1）＝﹣4kb ＜0，∴k 、b 同号．当k ＞0、b ＞0时，一次函数y ＝kx+b 的图象经过第一、二、三象限；当k ＜0、b ＜0时，一次函数y ＝kx+b 的图象经过第二、三、四象限．故选：A题型四：一次函数图像平移问题（要点：左加右减（在x 上），上加下减（在y 上））例题4将一次函数23y x =-+的图像沿x 轴向左平移4个单位长度后，得到的新的图像对应的函数关系式为（ ）A ．25y x =--B ．211y x =-+C ．27y x =-+D ．21y x =--【答案】A直接利用一次函数平移规律“上加下减”、“左加右减”即可得到答案．将一次函数y ＝﹣2x +3的图像沿x 轴向左平移4个单位长度，平移后所得图像对应的函数关系式为：2(4)3y x =-++，即y ＝﹣2x -5．故选：A ．题型五：一次函数的图像与坐标轴交点问题（利用坐标轴上点的坐标特点可解）例题5已知方程ax ＋b ＝0的解为x ＝32-，则一次函数y ＝ax ＋b 图象与x 轴交点的横坐标为（ ）A ．3B ．23-C ．﹣2D ．32-【答案】D 【解析】关于x 的一元一次方程ax ＋b ＝0的根是x ＝32-，即x ＝32-时，函数值为0，所以直线过点（32-，0），于是得到一次函数y ＝ax ＋b 的图象与x 轴交点的坐标．解：方程ax ＋b ＝0的解为x ＝32-，则一次函数y ＝ax ＋b 的图象与x 轴交点的坐标为（32-，0），即一次函数y ＝ax ＋b 图象与x 轴交点的横坐标为32-．故选：D ．拓展题：在平面直角坐标系中，点O 为原点，点(1,0)A ，直线3y kx =-交x 轴于点B ，交y 轴于点C ，若ABC D 的面积6，则k =（ ）A ．±1B ．35±C ．1或35-D ．1-或35【答案】D利用一次函数图象上点的坐标特征可得出点B ，C 的坐标，进而可得出OC ，AB 的长，利用三角形的面积公式结合ABC D 的面积为6，即可得出关于k 的方程，解之即可得出结论．解：当0x =时，033y k =´-=-，\点C 的坐标为(0,3)-，3OC =；当0y =时，30kx -=，解得：3x k=，\点B 的坐标为3(k，0)，3|1|AB k=-．162ABC S AB OC D ==Q g ，即133|1|62k´-=，解得：1k =-或35k =．故选：D ．题型六：利用一次函数图像或者解不等式求自变量或函数值的范围关键词：数形结合、几何法、代数法、一次函数与不等式例题6一次函数2y kx =+与x 轴交于点(4,0)A ，则不等式21kx +<的解是（ ）A ．2x >B ．2x <C ．2x >-D ．2x <-【答案】A 【解析】先由题意求出一次函数表达式，然后再求解不等式的解集即可．解：由题意得：把点A 坐标代入解析式得：042k =+，解得1k=2-；\一次函数解析式为：122y x =-+，\1212x -+<，解得2x ＞；故选A ．题型七：直线的倾斜程度与k 的大小关系例题7 帮练习第7题题型八：一次函数与其他函数相交问题例题8如图在平面直角坐标系中，直线y 6x =-+分别与x 轴、y 轴交于点A 、B ，与()y 0kx x=>的图象交于点C 、D ．若CD =13AB ，则k 的值为（ ）A ．4．B ．6．C ．8．D ．10．【答案】C 【解析】先求出点A 、B 的坐标，于是可得AB 的长，进而可得CD 的长，设C 、D 的横坐标分别为a ，b ，则a ，b 是联立y ＝﹣x +6和y ＝kx并整理后的方程的解，由CD b -并结合根与系数的关系可得关于k 的方程，解方程即可求出k ，从而可得答案．解：对直线y ＝﹣x +6，令x ＝0，则y ＝6，令y ＝0，则x ＝6，∴点A 、B 的坐标分别为（6，0）、（0，6），∴OB ＝OA ＝6，∴AB＝＝3CD，∠BAO=45°，∴CD=，联立y＝﹣x+6和y＝kx并整理得：x2﹣6x+k＝0，设点C、D的横坐标分别为a，b，则a+b＝6，ab＝k，∵∠BAO=45°，∴CD b-，∴CD2＝2（a﹣b）2＝2[(a+b)2﹣4ab]＝2（36﹣4k）＝（）2，解得：k＝8．故选：C．题型九：一次函数的几何综合问题例题9已知直线y=x轴，y轴分别交于,A B两点，在x轴上取一点P，使得PABD是等腰三角形，则符合条件的点P有（）个A．2B．3C．4D．5【答案】A【解析】根据等腰三角形的性质进行分类讨论：以AB为腰和底进行讨论即可求解．解：由题意，如图：Q 直线y =x 轴，y 轴分别交于,A B 两点，\()(1,0,A B ，\1,OA OB ==在Rt AOB V 中，2AB =，\∠ABO=30°，∠OAB=60°，又Q 在x 轴上取一点P ，使得PAB D 是等腰三角形，\①当AB=AP=2时，在x 轴上有()()123,0,1,0P P -；②当BP=AP 时，易得△ABP 为等边三角形，则有AB=BP=AP=2，所以()31,0P -；综上所述：符合条件的点P 有2个；故选A ．一、单选题1．一次函数3y x =-+的图像经过的象限是（ ）A ．一、二、三象限B ．一、二、四象限C ．一、三、四象限D ．二、三、四象限【答案】B 【解析】根据一次函数解析式k 和b 的符号，即可判定该函数图像经过的象限，即可解决．解：∵k ＜0∴一次函数图像y 随x 的增大而减小∵b ＞0∴图像交y 轴正半轴∴函数经过一、二、四象限故选B ．【点睛】本题主要考查了一次函数图形的性质，熟练k 和b 决定图像位置是解决本题的关键．2．直线1y x =+与y 轴的交点是（ ）A ．()1,0-B ．()1,0C ．()0,1D ．()1,1--【答案】C 【解析】根据y 轴上点的坐标特征：横坐标为0，将x=0代入直线解析式中即可求出结论．解：当x=0时，011y =+=∴直线1y x =+与y 轴的交点是()0,1故选C ．【点睛】此题考查的是求直线与y 轴的交点坐标，掌握y 轴上点的坐标特征：横坐标为0，是解决此题的关键．3．一次函数0y kx b kb =+，＜，且y 随x 的增大而增大，则其图象可能是( )A ．B ．C ．D ．【答案】A【解析】先根据一次函数y kx b =+中，y 随x 的增大而增大，且0kb ＜，判断出k 与b 的符号，再根据一次函数的图象与系数的关系进行解答．∵一次函数y kx b =+中，y 随x 的增大而增大，∴0k >，∵0kb ＜，∴0b ＜，∴一次函数y kx b =+的图象过一、三、四象限．故答案为：A ．【点睛】本题考查的是一次函数的图象与性质、一次函数的性质及不等式的基本性质，解决本题的关键是熟练掌握一次函数图像和系数的关系．4．如图，若一次函数y ＝﹣2x ＋b 的图象与两坐标轴分别交于A ，B 两点，点A 的坐标为(0，4)，则不等式﹣2x ＋b ＜0的解集为（ ）A．x＞2B．x＜2C．x＜4D．x＞4【答案】A【解析】首先把A点坐标代入一次函数解析式，算出b的值，进而可求出B点坐标，再结合图象可得不等式﹣2x＋b ＜0的解集．∵一次函数y＝﹣2x＋b的图象过A(0，4)，∴b＝4，∴函数解析式为y＝﹣2x＋4，当y＝0时，x＝2，∴B(2，0)，∴不等式﹣2x＋b＜0的解集为x＞2，故选：A．【点睛】此题主要考查一次函数与不等式的综合运用，熟练掌握，即可解题.5．某个一次函数的图象与直线162y x=+平行，并且经过点()2,4--，则这个一次函数的解析式为（）A．152y x=--B．132y x=+C．132y x=-D．28y x=--【答案】C 【解析】根据两直线平行时k 的值相等，设出所求解析式，把已知点坐标代入计算即可．由一次函数的图象与直线y ═12x ＋6平行，设直线解析式为y ＝12x ＋b ，把（−2，−4）代入得：−4＝−1＋b ，即b ＝−3，则这个一次函数解析式为y ＝12x−3．故选：C ．【点睛】此题考查了待定系数法求一次函数解析式，以及一次函数的图象，熟练掌握待定系数法是解本题的关键．6．如图，已知一次函数y kx b =+的图象与x 轴，y 轴分别交于点（2，0），点（0，3）．有下列结论：①关于x 的方程0kx b +=的解为2x =;②当2x >时，0y <；③当0x <时，3y <． 其中正确的是（ ）A ．①②B ．①③C ．②③D ．①③②【答案】A【解析】根据一次函数图象的性质，一次函数与一元一次方程的关系对各小题分析判断即可得解．由图象得：①关于x 的方程kx+b=0的解为x=2，故①正确；②当x>2时，y<0，故②正确；③当x<0时，y>3，故③错误；故选：A 【点睛】本题考查了一次函数图象的性质及一次函数与一元一次方程的关系，对于任意一个以x 为未知数的一元一次方程，它都可以转化为kx+b=0(k ≠0)的形式，解一元一次方程相当于在某个一次函数的函数y=kx+b 值为0时，求自变量的值．7．已知一次函数(3)1y a x b =+++的图象经过过一、二、四象限，那么a ，b 的取值范围是（ ）A ．3a >-，1b >-B ．3a <-，1b <-C ．3a >-，1b <-D ．3a <-，1b >-【答案】D【解析】由一次函数的图像经过过一、二、四象限可得：3a +＜0且1b +＞0,从而可得答案．解：因为一次函数(3)1y a x b =+++的图象经过过一、二、四象限，所以：3a +＜0且1b +＞0,所以：3a <-，1b >-，故选D ．【点睛】本题考查的是一次函数的图像的性质，同时考查一元一次不等式的解法，掌握一次函数的图像的性质是解题的关键．8．如图，四个一次函数y ax =，y bx =，1y cx =+，3y dx =-的图象如图所示，则a ，b ，c ，d 的大小关系是（ ）A ．b a d c>>>B ．a b c d >>>C ．a b d c >>>D ．b a c d>>>【答案】B【解析】根据一次函数和正比例函数的图象与性质可得．解：∵y ax =，y bx =经过第一、三象限，且y ax =更靠近y 轴，∴0a b >>，由∵ 1y cx =+，3y dx =-从左往右呈下降趋势，∴0,0c d <<，又∵3y dx =-更靠近y 轴，∴d c <，∴a b c d>>>故答案为：B ．【点睛】本题考查了一次函数及正比例函数的图象与性质，解题的关键是熟记一次函数及正比例函数的图象与性质．9．将直线y=3x 向左平移2个单位长度，再向上平移5个单位长度，平移后所得新直线的表达式为（ ）A ．()3-25y x =+B ．()325y x =++C ．()3-2-5y x =D ．()325y x =+-【答案】B【解析】根据直线的平移规律：上加下减，左加右减解答即可．解：将直线y=3x 向左平移2个单位长度，再向上平移5个单位长度，平移后所得新直线的表达式为()325y x =++．故选：B ．【点睛】本题考查了直线的平移，属于基本题型，熟练掌握一次函数的平移规律是解题关键．10．如图，点(,3)M m 在直线27y x =-+与直线21y x =-+之间（不在这两条直线上），则m 的取值范围是（ ）A ．12m -<<B ．02m <<C ．51m -<<D ．11m -<<【答案】A【解析】分别求出点M 在两条直线上时对应的m 的值，进而可得答案．解：当点(,3)M m 在直线27y x =-+上时，273m -+=，解得2m =，当点(,3)M m 在直线21y x =-+上时，213m -+=，解得1m =-；∵点(,3)M m 在直线27y x =-+与直线21y x =-+之间（不在这两条直线上），∴m 的取值范围为12m -<<．故选：A ．【点睛】本题考查了一次函数图象上点的坐标特征，属于常考题型，正确理解题意、熟练掌握一次函数的图象与性质是解题关键．二、填空题11．若一次函数()121y k x k =++- 的图象不经过第一象限，则k 的取值范围是_____【答案】k ＜-12【解析】根据一次函数图像所在的象限，得到关于k 的不等式组，进而即可求解．∵一次函数()121y k x k =++- 的图象不经过第一象限，∴1+2k ＜0，且k-1＜0，∴k ＜-12，且k ＜1，∴k ＜-12故答案是：k ＜-12【点睛】本题主要考查一次函数的系数与图像的关系，熟练掌握y=kx+b （k ≠0，k ，b 为常数）中，常数k ，b 的几何意义，是解题的关键．12．直线1:24l y x =+沿x 轴向右移动4个单位长度得到直线2l ，则直线2l 的解析式为______．【答案】24y x =-【解析】根据函数图象平移的方法：左加右减判断即可；直线1:24l y x =+沿x 轴向右移动4个单位长度得到：()2:24424=-+=-l y x x ；故答案是：24y x =-．【点睛】本题主要考查了一次函数图象的平移，准确分析判断是解题的关键．13．直线3y x =-+与x 轴，y 轴分别交与点,M N ，则点,M N 的坐标分别__________和__________【答案】()3,0 ()0,3【解析】分别把y=0或x=0代入解析式计算出对应的自变量和函数值，则可确定直线与x 轴、y 轴的交点坐标解：把y=0代入得-x+3=0，解得x=3；把x=0代入得y=3所以直线3y x =-+与x 轴、y 轴的交点坐标分别为()3,0，()0,3故答案为()3,0，()0,3【点睛】本题考查一元一次函数图象上的点的坐标特征，熟练掌握知识点是解此题的关键14．如图，直线y kx b =+分别交坐标轴于()5,0-，()0,3两点，则不等式0kx b +<的解集是__________．【答案】5x <-【解析】求0kx b +<的解集，就是求使一次函数y kx b =+的值小于0的自变量x 的取值范围．解：求0kx b +<的解集，从图象上可以看出当0y <时，5x <-．故答案为：5x <-．【点睛】本题考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y kx b =+的值大于（或小于）0的自变量x 的取值范围；从函数图象的角度看，就是确定直线y kx b =+在x 轴上（或下）方部分所有的点的横坐标所构成的集合．15．在一次函数y=kx+2中，若y 随x 的增大而增大，则它的图象不经过第 象限．【答案】四．【解析】一次函数y=kx+b 的图象有两种情况：①当k 0>，b 0>时，函数y=kx+b 的图象经过第一、二、三象限，y 的值随x 的值增大而增大；②当k 0>，b 0<时，函数y=kx+b 的图象经过第一、三、四象限，y 的值随x 的值增大而增大；③当k 0<，b 0>时，函数y=kx+b 的图象经过第一、二、四象限，y 的值随x 的值增大而减小；④当k 0<，b 0<时，函数y=kx+b 的图象经过第二、三、四象限，y 的值随x 的值增大而减小．由题意得，函数y=kx+2的y 的值随x 的值增大而增大，因此，k 0>．由k 0>，b 0>，知它的图象经过第一、二、三象限，不经过第四象限．16．已知一次函数y ＝kx+b 的图象经过一，二，四象限，且当2≤x ≤4时，4≤y ≤6，则b k的值是_____．【答案】-8【解析】利用一次函数的性质得到k＜0，则判断x＝2时，y＝6；x＝4时，y＝4，然后根据待定系数法求得k、b的值，即可求得bk的值．解：∵一次函数y＝kx+b的图象经过一、二、四象限，∴k＜0，∴函数y随x的增大而减小，∵当2≤x≤4时，4≤y≤6，∴当x＝2时，y＝6；当x＝4时，y＝4，∴26 44 k bk b+=ìí+=î，解得：18kb=-ìí=î，∴bk＝﹣8，故答案为：﹣8．【点睛】本题考查了一次函数的性质，一次函数图象上点的坐标特征以及待定系数法求一次函数的解析式，根据题意得出当x=2时，y=6；当x=4时，y=4是解题的关键．17．已知：一次函数y＝（2﹣m）x+m﹣3．（1）如果此函数图象经过原点，那么m应满足的条件为__；（2）如果此函数图象经过第二、三、四象限，那么m应满足的条件为__；（3）如果此函数图象与y轴交点在x轴下方，那么m应满足的条件为__；（4）如果此函数图象与y轴交点到x轴的距离为2，那么m应满足的条件为__．【答案】m＝3 2＜m＜3 m＜3且m≠2 m＝5或m＝1【解析】（1）将点（0，0）代入一次函数解析式，即可求出m的值；（2）根据一次函数的性质知，当该函数的图象经过第二、三、四象限时，2-m＜0，且m-3＜0，即可求出m 的范围；（3）先求出一次函数y=（2-m）x+m-3与y轴的交点坐标，再根据图象与y轴交点在x轴下方得到2-m≠0且m-3＜0，即可求出m的范围；（4）先求出一次函数y=（2-m）x+m-3与y轴的交点坐标，再根据图象与y轴交点到x轴的距离为2，得出交点的纵坐标的绝对值等于2，即可求出m的值．（1）∵一次函数y=（2﹣m）x+m﹣3的图象过原点，∴m﹣3=0，解得m=3．故答案为：m=3；（2）∵该函数的图象经过第二、三、四象限，∴2﹣m＜0，且m﹣3＜0，解得2＜m＜3．故答案为：2＜m＜3；（3）∵y=（2﹣m）x+m﹣3，∴当x=0时，y=m﹣3，由题意，得2﹣m≠0且m﹣3＜0，∴m＜3且m≠2．故答案为：m＜3且m≠2；（4）∵y=（2﹣m）x+m﹣3，∴当x =0时，y =m ﹣3，由题意，得2﹣m ≠0且|m ﹣3|=2，∴m =5或m =1．故答案为：m =5或m =1．【点睛】本题考查了一次函数与系数的关系：由于y=kx+b 与y 轴交于（0，b ），当b ＞0时，（0，b ）在y 轴的正半轴上，直线与y 轴交于正半轴；当b ＜0时，（0，b ）在y 轴的负半轴，直线与y 轴交于负半轴．k ＞0，b ＞0⇔y=kx+b 的图象在一、二、三象限；k ＞0，b ＜0⇔y=kx+b 的图象在一、三、四象限；k ＜0，b ＞0⇔y=kx+b 的图象在一、二、四象限；k ＜0，b ＜0⇔y=kx+b 的图象在二、三、四象限．也考查了一次函数图象上点的坐标特征以及一次函数的定义．18．已知一次函数y 1＝x ＋2与y 2＝－x ＋b （b 为常数），当x ＜1时，y 1＜y 2．则b 的取值范围是___________．【答案】b≥4【解析】由12y y <，求出b 2x 2-<根据x<1时，12y y <，列出b 212-³，解出不等式即可求出答案．∵12y y <，y 1＝x ＋2，y 2＝－x ＋b∴x+2<-x+b∴2x<b-2∴b 2x 2-< 又∵x<1时，12y y < ∴b 212-³∴b ≥4故答案为：b ≥4【点睛】本题考查了一次函数与不等式的关系，掌握函数与不等式的关系是解题的关键．19．已知直线4y kx =-与两坐标轴所围成的三角形面积等于4，则k 的值为________．【答案】±2【解析】求出直线与坐标轴的交点坐标或坐标表达式，根据三角形的面积公式建立关系式，即可求出k 的值．直线与y 轴的交点坐标为（0，﹣4），与x 轴的交点坐标为（4k，0），则与坐标轴围成的三角形的面积为14442k´´=，解得k=±2，经检验，k=±2是方程的解且符合题意，故答案为：±2．【点睛】本题考查了一次函数与坐标轴的交点与相关三角形的面积问题，要熟悉函数与坐标轴的交点的求法．20．在平面直角坐标系xOy 中，直线l ：1(0)y kx k =-¹与直线x k y k =-=-，分别交于点A B ，．直线x k =-与y =k -交于点C ．记线段AB ，BC AC ，围成的区域（不含边界）为W ．横，纵坐标都是整数的点叫做整点．（1）当2k =-时，区域W 内的整点个数为_____；（2）若区域W 内没有整点，则k 的取值范围是_______．【答案】6 01k <…或k=2【解析】（1）当2k =-时，直线21y x =--与直线22x y ，==的交点A B ，的坐标为：322æö÷ç-÷ç÷çèø， ，()2，-5，作出函数图像即可得出答案.（2）将k=1与k=2的函数图像作出，得出线段AB ，BC AC ，围成的区域（不含边界）无整点，即区域W 内没有整点.（1）解：如图示，当2k =-时，直线21y x =--与直线22x y ，==的交点A B ，的坐标为：322æö÷ç-÷ç÷çèø ，()2，-5，则，区域W 内的整点有（0，0），（0，1），（1，-2），（1，-1），（1，0），（1，1）共6个.（2）当1k =时，图像如下图示线段AB ，BC AC ，围成的区域（不含边界）无整点，当2k =时，图像如下图示线段AB ，BC AC ，围成的区域（不含边界）无整点，综上所述，由（1）的图像可知，当01k <…或k=2时，区域W 内没有整点.【点睛】本题考查的是一次函数图像的性质特点，解题的关键是要懂得根据题目的条件，画出相对应的函数图像.三、解答题21．已知一次函数122y x =+的图象与x 轴交于点A ，与y 轴交于点B ，求A ，B 两点的坐标并在如图的坐标系中画出此函数的图象．【答案】()4,0A -；()0,2B ；图象见解析．【解析】根据一次函数的解析式求出点A 、B 的坐标，然后利用五点作图法，最好使用列表-描点-连线的作图步骤作出图象．解：当x=0时，则有：2y =；当y=0时，则有：4x =-；∴点()4,0A -，点()0,2B ，∴函数图像如图所示：【点睛】本题主要考查一次函数的图像，熟练掌握一次函数图像的画法是解题的关键．22．画出函数y=-2x+2的图象，结合图象回答下列问题：（1）这个函数中，随着自变量x的增大，函数值y是增大还是减小？它的图象从左到右怎样变化？（2）当x取何值时，y=0？（3）当x取何值时，y＜0？【答案】（1）见详解；（2）x=1；（3）x＞1【解析】（1）画出函数图像，由图像可得；y随着x的增大而减小，图像从左至右下降；（2）由图像可得，当x=1时，y=0；（3）由图像可得，当x＞1时，y＜0.（1）函数y=－2x+2的图象为：由图象知：这个函数中，随着x的增大，y将减小，图象从左向右下降；（2）由图象知：当x=1时，y=0；（3）由图象知：当x＞1时，y＜0.23．一次函数y＝kx+b的图象如图所示：（1）求出该一次函数的表达式；（2）当x＝10时，y的值是多少？（3）当y＝12时，x的值是多少？【答案】（1）y＝x﹣2．（2）8；(3)14【解析】【解析】（1）观察函数的图象，得出一次函数经过点（2，0）（0，﹣2），代入函数解析式即得出一次函数的表达式．（2）（3）再分别令x＝10和y＝12，即可得出对应的y，x的值．解：（1）观察图象可得一次函数的图象经过点（2，0），（0，﹣2）代入函数的解析式y＝kx+b中，得202k bb+=ìí=-î，解得k1b2=ìí=-î，∴一次函数的表达式为y＝x﹣2．（2）令x＝10，得y＝10﹣2＝8（3）令y＝12，得x＝12+2＝14．【点睛】本题考查了待定系数法求一次函数的解析式，比较简单，同学们要熟练掌握．24．已知一次函数的图像经过()1,5A --和()1,1B 两点.（1）求这个一次函数的解析式；（2）若点(),1C a a -+在这个一次函数的图象上，求a 的值.【答案】(1)函数的解析式是：y=3x−2；(2) a=0.75.【解析】（1）设函数的解析式是y=kx+b ，把A （-1，-5）和B （1，1）代入函数的解析式，然后解方程组即可求解；（2）把点C 代入一次函数的解析式中，列方程可得a 的值．(1)设函数的解析式是y=kx+b ，根据题意得：53k b k b -+=-ìí+=î，解得：32k b =ìí=-î，则函数的解析式是：y=3x−2；(2)∵点C(a,−a+1)在这个一次函数的图象上，∴−a+1=3a −2a=0.75.【点睛】本题考查一次函数图象上点的坐标特征和待定系数法求一次函数解析式，解题的关键是掌握待定系数法求一次函数解析式.25．如图，已知直线123y x =-+和21y mx =-分别交y 轴于点A ，B ，两直线交于点()1,C n ．（1）求m ，n 的值；（2）求ABC V 的面积．【答案】（1）2m =，1n =；（2）△ABC 的面积为2．【解析】（1）先利用直线1y 求出点C 坐标，再利用直线2y 求出m 的值．（2）两个函数图象与y 轴的交点为A 、B ，即x=0时，可以求出A 、B 坐标，即可得出三角形面积．解：（1）∵两直线交于点()1,C n ∴将()1,C n 代入123y x =-+得：n=-2+3=1即：C 点坐标为：（1,1）将C （1,1）代入21y mx =-得：m-1=1即：m=2故：m=2，n=1．（2）∵当x=0时，13y =∴A （0,3）当x=0时，2-1y =∴B （0，-1）∴11141222ABC S AB D =´=´´= 故：△ABC 的面积为2．【点睛】本题属于一次函数的基础题型，根据已知点求出函数解析式，然后利用解析式求出点坐标，并求出三角形面积．26．直线2y x =--与x 轴相交于A 点，与y 轴相交于B 点，直线24(0)y kx k k =+->与直线2y x =--相交于C 点．（1）请说明24(0)y kx k k =+->经过点（4，2）；（2）1k =时，点D 是直线24(0)y kx k k =+->上一点且在y 轴的右侧，若2DOB DOA S S =V V ，求点D 的坐标；（3）若点C 在第三象限，求k 的取值范围．【答案】（1）见解析；（2）(4,2)D 或42,33D æö-ç÷èø；（3）113k <<【解析】（1）把x=4代入函数关系求出y 的值即可；（2）先求出A ，B 的坐标，进而求出OA ，OB 的值，再设点D 的坐标为(,2)a a -，根根据2DOB DOA S S =V V ，列出方程求解即可；（3）分别求出当直线24(0)y kx k k =+->经过点A ，B 时k 的值即可．解：（1）当4x =时，244242y kx k k k =+-=+-=∴点（4，2）在直线24(0)y kx k k =+->上．（2）∵直线2y x =--与x 轴相交于A 点，与y 轴相交于B 点∴(2,0)A -，(0,2)B -∴2OA OB==设D 的坐标为(,2)a a -∵2DOB DOA S S =V V ，∴2|2|a a =-，∴4a =或43a =，∴(4,2)D 或42,33D æö-ç÷èø（3）当直线24(0)y kx k k =+->经过点A 时，0224k k =-+-，解之得，13k =当直线24(0)y kx k k =+->经过点B 时，有224k -=-，解之得，1k =∴若点C 在第三象限，则113k <<．【点晴】本题考查了一次函数与一元一次方程，是一次函数的综合题，利用数形结合进行分析是解题的关键．27．如图，已知直线:4AB y x =+与直线AC 交于点A ，与x 轴交于点B ，且直线AC 过点(2,0)C 和点(0,1)D ，连接BD ．（1）求直线AC 的解析式．（2）求交点A 的坐标，并求出ABD △的面积．（3）在x 轴上是否存在一点P ，使得APD △周长最小？若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）112y x =-+；（2）(2,2)A -，3ABD S =V ；（3）存在点P 使APD △周长最小2,03P æö-ç÷èø．【解析】（1）设直线AC 解析式y kx b =+，代入(2,0)C ，(0,1)D ，用待定系数法解题即可；（2）将直线AB 与直线AC 两个解析式联立成方程组，转化成解二元一次方程组，再结合三角形面积公式解题；（3）作D 、E 关于x 轴对称，利用轴对称性质、两点之间线段最短解决最短路径问题，再用待定系数法解直线AE 的解析式，进而令0y =，解得直线与x 轴的交点即可．（1）设直线AC 解析式y kx b =+，把(2,0)C ，(0,1)D 代入y kx b =+中，得201k b b +=ìí=î，解得121k b ì=-ïíï=î，\直线AC 解析式112y x =-+．（2）联立1124y x y x ì=-+ïíï=+î，解得22x y =-ìí=î．(2,2)A \-，把0y =代入4y x =+中，得4x =-，(4,0)B \-，(2,0)C Q ，6BC \=，1162622ABC A S BC y \=×=´´=V ，1161322DBC D S BC y =×=´´=V ，633ABD ABC DBC S S S \=-=-=V V V ．故答案为：(2,2)A -，3ABD S =V ．（3）作D 、E 关于x 轴对称，PD PE \=，APD QV 周长AP PD AD =++，AD Q 是定值，AP PD \+最小时，APD △周长最小，AP PD AP PE AE +=+³Q ，\A 、P 、B 共线时，AP PE +最小，即AP PD +最小，连接AE 交x 轴于点P ，点P 即所求，(0,1)D Q ，D 、E 关于x 轴对称，(0,1)E \-，设直线AE 解析式y mx n =+，把(2,2)A -，(0,1)E -代入y mx n =+中，221m n n -+=ìí=-î，解得321m n ì=-ïíï=-î，312y x \=--，令0y =得3102x --=，23x =-，2,03P æö\-ç÷èø，即存在点P 使APD △周长最小2,03P æö-ç÷èø．【点睛】本题考查一次函数、二元一次方程组、轴对称最短路径问题、与x 轴交点等知识，是重要考点，难度较易，掌握相关知识是解题关键．。