电网络---第七章网络的灵敏度分析

2023年博士生入学考试初试科目考试大纲
科目名称：电网络理论
一、考试总体要求
《电网络理论》是介绍现代电路分析中一些较为成熟和先进的内容,是了解现代电路理论的“窗口”。

牢记基本概念,掌握基本方法,与大学电路原理的内容有机地联系在一起。

掌握与电气工程及电子工程相关的电路理论的一些新思想、新方法、新元件和新进展。

综合利用所学知识解决复杂电路分析计算问题。

二、考试内容
1．网络理论基础：网络元件的新体系，网络的互联规律性以及网络及元件的基本性质，如（1）线性与非线性、（2）无源性和有源性、（3）时变性与时不变性、（4）互易性与非互易性等。

2.简单非线性电路：非线性电阻电路的基本概念和常用分析方法以及一、二阶非
线性动态电路的分析方法。

重点掌握低阶自治电路的定性分析。

3．多口网络：含源及无源多口网络的常见矩阵表示法，重点掌握不定导纳矩阵的计算方法及其应用。

4．电路的代数方程：电路代数方程的矩阵形式，混合分析法，稀疏表格法和改进节点法，重点掌握混合分析法和改进节点法。

5．动态电路的时域方程：网络分析的状态变量法，状态方程的列写，线性状态方程的解析解法，重点掌握含有高阶元件、非线性元件或非常态电路的状态方程的列写。

6．网络的灵敏度分析：灵敏度分析的意义和在本专业分析计算中的主要应用，重点掌握伴随网络法。

三、考试题型
证明题、计算题、论述题
四、参考书目
1．梁贵书．高等电网络．讲义．．2.．高等电力网络分析． 2007。

基于网络分析的输电线路灵敏度分析及优化随着经济的快速发展和城市化进程的加速，电力需求量不断增长，而输电电力的可靠性和稳定性成为电网建设和运营中不可忽视的问题。

因此，对于输电线路灵敏度的研究变得越来越重要。

本文将通过网络分析来探讨输电线路灵敏度的分析和优化方法。

一、网络分析简介网络分析是指研究由节点和连接组成的网络的性质和行为的一种方法。

它广泛应用于社交网络、电力系统、物流系统等领域。

网络分析的核心是节点和连接的度量，即节点的度和连接的度。

节点的度是指与该节点直接相连的节点数，连接的度是指该连接所连接的两个节点的度之和。

对于输电电力系统，可以将输电线路抽象成为一个网络，不同的节点代表着不同的电力设备或输电线路，连接代表着电力设备或输电线路之间的关系。

通过对输电系统进行网络分析，可以揭示出系统中的节点和连接性质，以及系统的全局性质。

二、输电线路灵敏度分析方法线路的灵敏度反应了输电系统在发生故障或负荷突变时的稳定性和鲁棒性。

在电力系统实际运行中，输电线路的负荷、故障或其他影响因素会导致系统功率流分布产生相应的变化，从而影响系统的稳定性和可靠性。

因此，对于输电系统的灵敏度分析是电力系统运行和管理的重要手段。

1. 线性灵敏度分析线性灵敏度分析是一种基于微小扰动的分析方法，它通过分析输电系统在变化负荷或节点短路等情况下的功率流分布的变化，从而推导出输电线路的灵敏度。

其基本思想是将输电系统的非线性方程线性化，然后对线性化方程进行求解。

在这个基础上，可以通过统计分析、多项式拟合等方法来分析线路的灵敏度情况。

2. 非线性灵敏度分析相对而言，非线性灵敏度分析方法更加适用于现代复杂的输电系统。

它通过对整个系统在不同负荷、风速、短路等条件下的进行仿真计算，并通过计算机模拟的方法来分析系统的灵敏度。

三、输电线路灵敏度优化方法通过灵敏度分析，我们可以找到系统中灵敏度较弱的部分，然后对其进行优化，以提高系统的稳定性和鲁棒性。

电网络理论考题总结（简答题）【1】N端口线性时变与非线性的电感元件、电容元件的定义，并举例。

线性时变电感：N端口元件满足关系，且为矩阵，与Ψ=L i(t)L(t)(N-1)×(N-1)磁链及电流无关。

线性时变电容：N端口元件满足关系，且为矩阵，与q=C v(t)C(t)(N-1)×(N-1)电荷及电压无关。

（电阻定义类似）☛☛☛一个不含时变元件的电路称为时不变电路，否则为时变电路。

若一个电容元件的库伏特性不是一条通过坐标原点的直线，该种电容就是非线性电容；电感的磁通链和电流间的函数关系为韦安特性，若电感元件的韦安特性不是一条过坐标原点的直线，则为非线性电感元件。

【2】N端口非线性电路的定义。

一是根据电路元件的特性来定义（含非线性元件即为非线性电路）；二是根据输入输出关系来定义（端口型定义，网络输入输出关系不同时存在可加性和齐次性时即为端口型非线性网络）。

【3】高阶有源滤波器的设计步骤。

（根据相应实例写步骤）一般：高阶：给出设计指标，根据设计指标选择逼近函数；确定阶数、找到对应的无源网络模型；选择实现方法（级联、多路反馈、无源模拟等）；参数退归一化；注意补偿、修正电路（直流通路）。

选取逼近函数类型；根据设计要求确定阶数；找到对应逼近函数的无源低通网络模型；选择实现方法（级联、多路反馈、无源模拟等）；根据要求的滤波器类型进行变换（如仿真电感、F D N R、L F等）；参数退归一化。

二阶：S a l l e n K e y---L P、H P、B P、高通、陷波或者双积分回路---K H NT T。

【4】高阶有源滤波器的分类。

按使用的器件：仿真电感、F D N R、C CⅡ、跨导电容、运放；按设计方法：级联法、多路反馈法、无源模拟法。

【5】高阶有源滤波器的设计方法，它们的共同点和特点。

❶级联法：级联滤波器易于调节和优化动态范围，但设计时各极、零点的搭配要慎重考虑，以实现较低灵敏度。

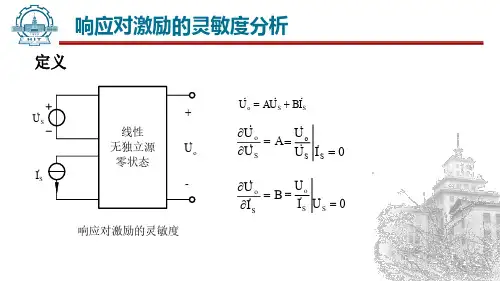
响应对激励的灵敏度分析 线性
无独立源零状态S U
S I -
o
U
+
o S S U AU BI =+A U U =∂∂S o B I U =∂∂S o 响应对激励的灵敏度定义 o S 0S U U I ==o 0S S U I U ==
互易定理1：对于含有一个独立电压源和若干线性二端电阻的电路，当此电压源在某一端口A 作用时,在另一端口B 产生的短路电流等于把此电压源移到端口B 作用而在端口A 所产生的短路电流。

电压、电流的参考方向见图 N S U S S
ˆU U =o o ˆI I =o I N ˆ
互易定理2：对于含有一个独立电流源和若干线性二端电阻的电路，当此电流源在某一端口A 作用时，在另一端口B 产生的开路电压等于把此电流源移到端口B 作用而在端口A 所产生的开路电压。

电压、电流的参考方向见图 N -+o U S I S S
ˆ
I I =-=+
o
o ˆ
U U N ˆ
如果在数值上I s 与U s 相等，则U 0与 在数值上也相等。

其中I s 与 及U s 与 U 0 分别取同样单位。

0ˆI N o
U +-S U S S ˆI U =o o ˆU I -=N ˆ0ˆI 定理3：对于 图所示电路，。

电网络第七章网络的灵敏度分析第七章网络的灵敏度分析网络的灵敏度分析是指对网络中各个节点或边的变化进行分析，以评估网络对这些变化的敏感程度。

通过灵敏度分析，我们能够更好地了解网络中的关键节点和关键边，从而为网络的优化设计和保护提供有力的支持。

本章将介绍网络的灵敏度分析方法和应用，并对其在实际网络中的价值进行探讨。

一、网络的灵敏度分析方法1.1 传统方法传统的网络灵敏度分析方法主要基于线性系统理论，通过计算网络在节点变化或边删除时的响应情况来评估网络的灵敏度。

其中，常用的方法包括雅可比矩阵法、拉普拉斯矩阵法等。

这些方法在对简单网络进行分析时较为有效，但在面对复杂网络时往往会遇到计算复杂性高、求解难度大等问题。

1.2 基于复杂网络理论的方法随着复杂网络理论的发展，越来越多的灵敏度分析方法基于复杂网络理论而提出。

这些方法可以更好地应对复杂网络的特点，包括节点之间的异质性、非线性关系等。

其中，常用的方法包括基于节点介数的方法、基于度中心性的方法、基于小世界网络理论的方法等。

二、网络的灵敏度分析应用2.1 网络优化设计灵敏度分析可以帮助我们识别网络中的关键节点和关键边，从而为网络的优化设计提供指导。

通过对网络的灵敏度进行分析，我们可以发现网络中的薄弱环节，针对这些薄弱环节进行改进，提高网络的鲁棒性和可靠性。

2.2 网络安全防护网络的灵敏度分析在网络安全防护中有着广泛的应用。

通过对网络的灵敏度进行分析，我们可以了解网络中的关键节点和关键边，当这些节点或边受到攻击或破坏时，网络的整体性能会受到较大的影响。

基于这些分析结果，我们可以采取相应的安全策略，加强对网络中的关键节点和关键边的保护，提高网络的抗攻击能力。

2.3 社交网络分析灵敏度分析在社交网络分析中也有着重要的应用。

社交网络中的节点代表人员，边代表人员之间的关系。

通过对社交网络的灵敏度进行分析，我们可以了解社交网络中的核心人物和关键关系，从而更好地理解社交网络的结构和特性，为社交网络的管理和决策提供参考。

1. （15%）图示电路中，求传递函数iU U s H 0)(=对流控电压源的控制系数2r 变化的灵敏度Hr S 2（分别用直接微分法和伴随网络法），V r 1,52=Ω=i UiU0U +-1题图2. （15%）推导回转器的伴随网络及其灵敏度公式rT∂∂，其中回转器的伏安关系为 ⎩⎨⎧=-=1221ri u ri u ，参考方向与标准二端口网络端口方向相同。

3. （15%）用伴随网络法计算图示电路输出电压U o 对电导的灵敏度（5,4,3,2,1=∂∂j jo G U ）。

2V1/2Ω2A4.（20%）图示电路中10s u V =，1234511()G G G G G S =====Ω，受控源的控制系数分别为2α=，4β=，用伴随网络法求灵敏度,1,2,3,4,5O j I j G ∂=∂，OI α∂∂和OI β∂∂。

5. （20%）图示一端口单口网络中，12R =Ω，22R =Ω，2α=， 12R =Ω，3333112(,)2G S G R R ===Ω。

设单口网络的输入电阻为in R ，用伴随网络法求in 1R R ∂∂、in 3R G ∂∂和in Rα∂∂。

G 5G 4G 3G 1. U S5题图2R 5题图6.（20%）图示电路的转移电阻定义为t R （otsU R I =），试用伴随网络法计算灵敏度(1,2,3,4,5)tjR j G ∂=∂和tR α∂∂。

7.（15%）图示电路中10s u V =，1234511()G G G G G S =====Ω，受控源的控制系数分别为2α=，4β=，用伴随网络法求灵敏度,1,2,3,4,5O j I j G ∂=∂，O Iα∂∂和OI β∂∂。

G 5G 4G 3G U S6题图I s222I I α=12Ω7题图8.（10%）试推导理想变压器的伴随网络及其灵敏度公式Tn∂∂，其中T 为网络函数，n 为变比9. （10%）图示电路的转移电阻定义为t R （o t sU R I =），其中10s I A =。

第七章 网络的灵敏度分析第一节 灵敏度分析的意义p281第二节 灵敏度分析基本概念一．灵敏度 1．p281 定义 2．分类（1） 绝对灵敏度（微分灵敏度）（非归一化灵敏度）xTx T D x Tx ∆∆=∂∂=→∆0lim （式7－2－1） （2） 相对灵敏度（归一化灵敏度）xTx x TTx T T x S T x ln ln ∂∂=∂∂=∂∂=（式7－2－1） （3） 其他灵敏度表示法·xTx S Tx ∂∂=100 （参数变化百分之一时）·xTx S xT x S T x T x∂∠∂=∂∂=∠180100 ·半归一化灵敏度x Tx T xS T Tx ln 0∂∂=∂∂== xT x T T S x Tx ∂∂=∂∂==ln 10·多参数灵敏度（只能用于参数的微小变化） p282)(),(21x T x x x T T n ==)()(21)()()(0000x x H x x x x T x T x T T T --+-⋅∇=-=∆ 较高精度 其中：⎥⎦⎤⎢⎣⎡∂∂∂∂∂∂=∆n x T x T x T T 21, 3．解析灵敏度公式 p283 （1）2121Tx Tx TT x S S S +=（2）)(121212121T x T x T T x S T S T T T S ++=+ 证明见“书”（3）Tx T xnS S n=（4）Tx T xS S -=1 （5）Tx Tx S S -=1（6）设)()()(ωθωωj e H j H = ，则)()()()(ωθωωωθxH x j H xS j S S += 证明：（补充）θθθθθθθθθθθθθθxH x H x j j H x j j j j j He xS j S xj x S x j He Hex S x e H x H e He x x He He x S j ⋅+=∂∂+=∂∂⋅⋅+=∂∂+∂∂=∂∂=)()( （7）T 是常量，0=Tx S 4．应用p284 例7－2－1（自己看）第三节 伴随网络法（Adjoint Network ）一．概念引入伴随网络目的（1）原网络N ：线性时不变网络，且内部不含独立源。

电⽹络第⼀讲（⼤纲125）讲义——电⽹络理论讲义（⼀）1 ⽹络元件和⽹络的基本性质1.1 ⽹络及其元件的基本概念1.1.1 ⽹络的基本表征量（1）基本表征量分为三类：1）基本变量：电压u (t )、电流i (t )、电荷q (t )和磁链Ψ(t )。

2）基本复合量：功率P (t )和能量W (t )。

3）⾼阶基本变量：()uα和()iβ()0 1αβ≠-、，()d d k k k xxt =，2()112...()...ktt t k kx x d d d ττττ--∞-∞-∞=0k ?? ?>例如，22d d i u E t =，22d d u i D t =等基本变量和⾼阶基本变量⼜可统⼀成()u α和()i β两种变量，其中α和β为任意整数。

（2）基本表征量之间存在着与⽹络元件⽆关的下述普遍关系：()()d t u t dt ψ=(1)()()tt u u d ττ--∞ψ==?()()dq t i t dt =(1)()()tq t ii d ττ--∞==?()()()()dW t p t u t i t dt ==()()()()t t W t p d u i d τττττ-∞-∞==??（3）容许信号偶和赋定关系可能存在于（多⼝）元件端⼝的电压、电流向量随时间的变化或波形称为容许的电压—电流偶，简称容许信号偶，记作{}(),()t t u i 。

3Ω电阻的伏安关系为，3u i =，{}3cos ,cos t t ωω是容许信号偶，｛3, 1｝不是容许信号偶。

容许信号偶必须是向量或者时间的函数。

元件所有的容许信号偶的集合，称为该元件的赋定关系（本构关系) 。

（3）基本⼆端代数元件基本⼆段元件的定义为：()()()()(){}, , , ,u i u q i q ηθ∈ψψ，，，，或(), 0f ηθ=例如线性电阻元件u=iR , 电容元件q=Cu 等。

如图所⽰。

⼀般性分类：η控元件：θ＝θ(η) θ控元件：η＝η(θ)单调元件：元件既是η控的,⼜是θ控的多值元件：元件既不是η控的,也不是θ控的这个概念与数学上的函数定义可以类⽐，若η是θ的函数，则元件是θ控元件；若θ是η的函数，则元件是η控元件；若函数单调，元件既是η控的,⼜是θ控的；若η不是θ的函数，且θ也不是η的函数，则元件既不是η控的,也不是θ控的。