信息论与编码 第四章 (1)
- 格式:docx
- 大小:30.68 KB
- 文档页数:4








《信息论与编码》课程教学大纲一、课程基本信息课程代码:16052603课程名称:信息论与编码英文名称:Information Theory and Coding课程类别:专业课学时:48学分:3适用对象:信息与计算科学考核方式:考试先修课程:数学分析、高等代数、概率论二、课程简介《信息论与编码》是信息科学类专业本科生必修的专业理论课程。
通过本课程的学习,学生将了解和掌握信息度量和信道容量的基本概念、信源和信道特性、编码理论等,为以后深入学习信息与通信类课程、为将来从事信息处理方面的实际工作打下基础。
本课程的主要内容包括:信息的度量、信源和信源熵、信道及信道容量、无失真信源编码、有噪信道编码等。
Information Theory and Coding is a compulsory professional theory course for undergraduates in information science. Through this course, students will understand and master the basic concepts of information measurement and channel capacity, source and channel characteristics, coding theory, etc., lay the foundation for the future in-depth study of information and communication courses, for the future to engage in information processing in the actual work.The main contents of this course include: information measurement, source and source entropy, channel and channel capacity, distortion-free source coding, noisy channel coding, etc。


第4章无失真信源编码习题及其参考答案4-1 有一信源,它有六个可能的输出,其概率分布如下表所示,表中给出了对应的码A、B、C、D、E和F(1)求这些码中哪些是唯一可译码;(2)求哪些码是及时码;(3)对所有唯一可译码求出其平均码长l。
4-2 设信源61261126()1()()()()iis s sXp sp s p s p sP X=⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦∑。
对此次能源进行m元唯一可译编码,其对应的码长为(l1,l2,…,l6)=(1,1,2,3,2,3),求m值的最好下限。
(提示:用kraft不等式)4-3设信源为1234567811111111()248163264128128s s s s s s s sXp X⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦,编成这样的码:(000,001,010,011,100,101,110,111)。
求(1)信源的符号熵;(2)这种码的编码效率;(3)相应的仙农码和费诺码。
4-4求概率分布为11122(,,,,)3551515信源的二元霍夫曼编码。
讨论此码对于概率分布为11111(,,,,)55555的信源也是最佳二元码。
4-5有两个信源X和Y如下:121234567()0.200.190.180.170.150.100.01X s s s s s s s p X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦123456789()0.490.140.140.070.070.040.020.020.01Y s s s s s s s s s p Y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦(1)用二元霍夫曼编码、仙农编码以及费诺编码对信源X 和Y 进行编码,并计算其平均码长和编码效率;(2)从X ,Y 两种不同信源来比较三种编码方法的优缺点。
4-6设二元霍夫曼码为(00,01,10,11)和(0,10,110,111),求出可以编得这样 霍夫曼码的信源的所有概率分布。
4-7设信源为12345678()0.40.20.10.10.050.050.050.05X s s s s s s s s p X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,求其三元霍夫曼编码。
4.1某离散无记忆信源概率空间为分别使用长度为10和100的序列进行等长无失真编码,分别计算最短平均码长和编码效率。
解:信源的熵为881.03.03.07.07.0)(H =--=lb lb X 比特/符号当N=10时,序列码长应当满足 81.81881.0102)(L 1=⨯=>lb X NH 比特/序列考虑到序列码长应该为整数,取L1=9比特/符号,平均每个符号的码长为9.0NL L 11==比特/符号 所以编码效率为%9.97L )(H 11==X η 当N=100时,序列码长为1.881881.01002)(L 1=⨯=>lb X NH 比特/100符号取L1=89比特/符号,平均每个符号的码长为89.0NL L 22==比特/符号 编码效率为%99L )(H 22==X η 4.2设离散无记忆信源为如果要求编码效率为,允许错误概率为,求编码序列的长度。
解:信源的熵为722.02.02.08.08.0)(H =--=lb lb X 比特/符号自信息量方差为64.0722.0-)2.0(2.0)8.0(8.0D 222=+=lb lb采用二进制码进行等长编码,序列长度应当满足72221062.1)1)((D N ⨯=-≥δηηX H4.3设离散无记忆信源的概率空间为要求编码效率为(1) 如果采用序列等长编码,而允许译码错误概率为,求编码序列的长度。
(2) 如果采用序列变长编码,求编码序列的长度,并且与(1)比较,说明为什么会有这样的结果。
解1)信源的熵为811.025.025.075.075.0)(H =--=lb lb X 比特/符号自信息量方差为471.0811.0-)25.0(25.0)75.0(75.0D 222=+=lb lb采用二进制编码,序列长度为62221029.1)1)((D N ⨯=-≥δηηX H2)对信源进行二次扩展,并采用下列编码方式构成唯一可译码平均码长为6875.13161316321631169L =⨯+⨯+⨯+⨯=比特/2符号 每个符号码长为84375.026875.12L L ===比特/符号 编码效率为%95%1.9684375.0811.0L H(X)=>===δη 由于变长编码能够更好利用不同序列的概率分布进行编码,概率越大,序列的码长越短,概率越小,序列的码长越长,所以相对等长编码而言,变长编码的平均码长很短。
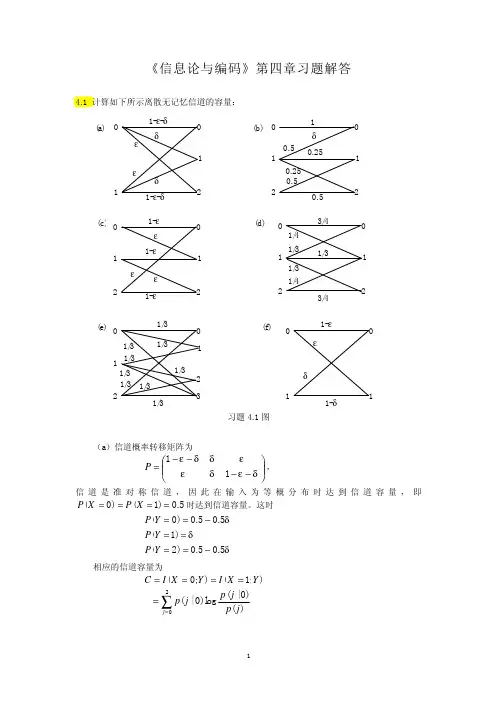
4-1 设有一个二元等该率信源{}1,0∈X ,2/110==p p ,通过一个二进制对称信道(BSC )。
其失真函数ij d 与信道转移概率ij p 分别定义为j i j i d ij =≠⎩⎨⎧=,0,1 ,j i j i p ij =≠⎩⎨⎧-=,1,εε 试求失真矩阵d 和平均失真D 。
解:由题意得,失真矩阵为d ⎥⎦⎤⎢⎣⎡=0110d ,信道转移概率矩阵为P ⎥⎦⎤⎢⎣⎡--=εεεε11)(i j 平均失真为εεεεε=⨯-+⨯+⨯+⨯-==∑0)1(211211210)1(21),()()(,j i d i j p i p D ji 4-3 设输入符号与输出符号X 和Y 均取值于{0,1,2,3},且输入符号的概率分布为P(X=i)=1/4,i=0,1,2,3,设失真矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0111101111011110d 求)(),(,,max min max min D R D R D D 以及相应的编码器转移概率矩阵。
解:由题意,得 0min =D.则symbol bit X H R D R /24log )()0()(2min ====这时信源无失真,0→0,1→1,2→2,3→3,相应的编码器转移概率矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000010*********)j (i P ∑===303,2,1,0max ),()(min i j j i d i p D,,141141041141141141141041min{⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯=}041141141141141041141141⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯, 43}43,43,43,43min{== 则0)(max =D R此时输出概率分布可有多种,其中一种为:p(0)=1,p(1)=p(2)=p(3)=0 则相应的编码器转移概率矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001000100010001)(i j P]4-5 具有符号集{}10,u u U =的二元信源,信源发生概率为:2/10,1)(,)(10≤<-==p p u p p u p 。
信息论与编码 第四章
4.5判断以下几种信道是不是准对称信道
(1)⎥⎦
⎤⎢⎣⎡3.02.05.05.03.02.0不是
(2)⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡7.03.06.04.03.07.0不是 (3)⎥⎦
⎤⎢⎣⎡7.01.02.02.01.07.0是
(4)⎥⎦
⎤⎢⎣⎡6/13/13/16/16/16/13/13/1 是 4.7计算以下离散无记忆信道DMC 的容量及最佳分布
(1)P=⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡---p p p p p p 101001
解:
此为对称信道,达到C 需要等概,则该信道的最佳分布为:
X q (X ) = x1 x2 x313 13 13
所以该信道的容量为:C=log 3+(1-p )log(1−p)+p log p =log3-H 2(p )
(2)P=⎥⎦⎤⎢⎣⎡----2/)1(2/)1(2/2
/2/2/2/)1(2/)1(p p p p p p p p
解:
易得该信道为一个准对称信道,假定最佳分布为:
X q (X ) = x1 x2 13 13
s1= (1−p)/2p/2p/2(1−p)/2 s2= (1−p)/2p/2p/2(1−p)/2
C=log k - N s *log M s -H
=log 2-(1/2*log 1/2+1/2*log 1/2)+(1-p)log(1−p)/2+p log p =log2+(1-p)log(1−p)/2+p log p
=log2-H 2(p )
(5)P= 132323
13
解:
C=log 2+13×log 13+23×log 23 =0.083
4.10给定离散信道的信道转移概率矩阵P=⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡----q q q q p p p p 100100001001,计算其信道容量C
解:
s1= 1−p p p 1−p s2= 0000
S3= 0000
s4= 1−q q q 1−q C=log 4+(1-p)log(1−p)+p log p +(1-q)log(1−q)+q log q
4.11给定离散信道P=
0.30.70.50.5
,计算信道容量C 解:
P −1= −2.5 3.52.5−1.5 H(Y |x 1)=-0.3ln 0.3-0.7ln 0.7=0.6
H(Y |x 2)=-ln 0.5=0.7
C=ln e {− p −1H}2i=12k=1
=ln[e 2.5∗0.6−3.5∗0.7+e −2.5∗0.6+1.5∗0.7]
=0
4.18 N 个同样的二进制对称信道BSC 级联,如图所示,各信道的转
移概率矩阵为P= p 1−p 1−p p
,证明它等价于一个转移概率为12[1-(1−2p)n ]的BSC ,且当n →∞时,信道容量C →0
图见P98
证明:P N =(1-P N −1)*P+P N −1*(1-P)=P N −1*(1-2P)+P
P N −1=P N −2*(1-2P)+P
P N −2=P N −3*(1-2P)+P
…
P 2=P 1*(1-2P)+P
P 1=P
=>P N =P N −1*(1-2P)+P
=[P N −2*(1-2P)+P]*(1-2P)+P =P N −2*(1−2P)2+P*(1-2P)+P =P N −3*(1−2P)3+P*(1−2P)2+P*(1-2P)+P
=P ∗(1−2P)N −1+P* (1−2P)I N −2I=0
=P (1−2P)I N −1I=0
=P*
1−(1−2P)N 1−(1−2P) =1−(1−2P)N 2
Q N =P{X N =0}=P{X 0=0}*(1-P N )+P{X 0=1}*P N C=0。