信息论与编码第四章

《信息论与编码》习题解答第四章 信息率失真函数-习题答案4.1解：依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡=0110d ，转移概率⎥⎦⎤⎢⎣⎡--=εεεε11)|(i j a b p 平均失真：εεεεε=⨯-⨯+⨯⨯+⨯⨯+⨯-⨯==∑∑==0)1(2/112/112/10)1(2/1),()|()(2121j i i j i j i b a d a b p a p D4.2解：依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡=0210d ， 0min =D ,∑=⨯+⨯=⨯+⨯===ij i i j j y x d x p D D )102/122/1(2/112/102/1),()(min min max 舍去当0min =D ，bit X H R D R 12log )()0()(min ====因为没有失真，此时的转移概率为⎥⎦⎤⎢⎣⎡=1001P当2/1max =D ，0)(max =D R因为取的是第二列的max D 值，所以输出符号概率:,1)(,0)(21==b p b p ,,2221b a b a →→因此编码器的转移概率为⎥⎦⎤⎢⎣⎡=1010P 4.3解：0min =D0041041041041),(min )(43041141141141),()(min min min max =⨯+⨯+⨯+⨯===⨯+⨯+⨯+⨯===∑∑i j i j i i j i i j j y x d x p D y x d x p D D 当0min =D ，bit X H R D R 24log )()0()(min ==== 因为没有失真，此时的转移概率为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000010000100001P 当4/3max =D ，0)(max =D R因为任何一列的max D 值均为3/4，所以取输出符号概率:0)(,0)(,0)(,1)(4321====b p b p b p b p ，即14131211,,,b a b a b a b a →→→→因此编码器的转移概率为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001000100010001P 4.4解： 依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡=4/1014/110d ， 0min =D∑=⨯+⨯===ij i i j j y x d x p D D )2/12(4/1)4/12/14/12/1min(),()(min min max 个均为其它当0min =D ，bit X H R D R 12log )()0()(min ====因为没有失真，此时的转移概率为⎥⎦⎤⎢⎣⎡=010001P 当4/1max =D ，0)(max =D R因为取的是第三列的max D 值为1/4，所以取输出符号概率:1)(,0)(,0)(321===b p b p b p ，即3231,b a b a →→因此编码器的转移概率为⎥⎦⎤⎢⎣⎡=100100P 4.5解：(1)依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡=0110d ，转移概率为：⎥⎦⎤⎢⎣⎡-=q q P 101 )1(0)1()1(1)1(1001),()|()(11p q q p q p p p y x d x y p x p D n i mj j i i j i -⨯=⨯-⨯-+⨯⨯-+⨯⨯+⨯⨯==∑∑==(2) 0min =D因为)(D R 是D 的递减函数，所以)1log()1(log )()()())(m ax (min min p p p p D H p H D R D R ----=-==当0=q 时可达到))(max(D R ，此时0=D(3) ∑-=⨯+⨯===iji i j j ，p p p p y x d x p D D )1(10),()(min min max 舍去更大另一个 因为)(D R 是D 的递减函数，所以0)()()())(m in(max max =-==D H p H D R D R当1=q 时可达到))(min(D R ，此时p D -=1(图略，见课堂展示)4.6解：依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡∞∞=1010d ，信源⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡2/12/110)(u p u 0min =D ，∑⨯+⨯⨯+∞⨯∞⨯+⨯===iji i j j y x d x p D D )12/112/1,02/12/1,2/102/1min(),()(min min max )(1]1,,m in[舍去另二个，∞=∞∞=10≤≤D因为二元等概信源率失真函数：⎪⎭⎫ ⎝⎛-=a D H n D R ln )( 其中1,2==a n ，所以率失真函数为：D D R -=1)(4.7解：失真矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=011101110d ，按照P81页方法求解。

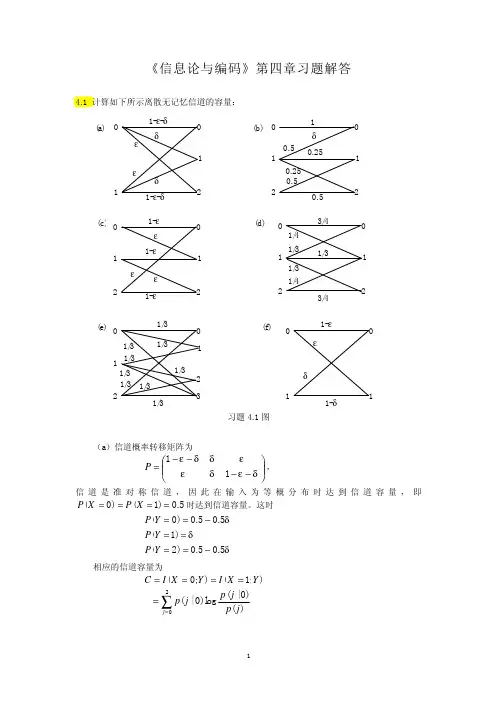
4.5若将N 个相同的BSC 级联如题图4.5所示，各信道的转移概率矩阵为⎥⎦⎤⎢⎣⎡--p p p p 11。

令Q t =P{X t =0}，t=0,1,…,N,且Q 0为已知。

题图 4.5(a)求Q t 的表达式。

(b)证明N →∞时有Q N →1/2，且与Q 0取值无关，从而证明N →∞级联信道的信道容量C N →0，P>0。

解：(a)对于满足X N 为马氏链的串联信道，他们总的信道转移概率矩阵为各个串联信道矩阵的乘积，即P(X N |X 0)= P(X 1|X 0) P(X 2|X 1)……P(X N |X N-1)由已知得，但各信道的转移概率矩阵为⎥⎦⎤⎢⎣⎡--p p p p 11 则两个信道级联的转移概率矩阵为： P 2=⎥⎦⎤⎢⎣⎡--p p p p 11⎥⎦⎤⎢⎣⎡--p p p p 11=()()()()⎥⎦⎤⎢⎣⎡-+---+2222112p 12p 1p p p p p p 三个信道级联的转移概率矩阵为： P 3=()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+----+33331221211221211221211-2p 2121p p p 四个信道级联的转移概率矩阵为： P 4=()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+----+44441221211221211221211-2p 2121p p p 以此类推：可得N 个信道级联的转移概率矩阵为：P N =()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+----+N N N N p p p 1221211221211221211-2p 2121 则Q t =P{X t =0}=()()()()()000121221211122121122121Q p p Q p Q p t t t t -+--=-⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡-+即Q t 的表达式为：Q t =()()012122121Q p p t t -+-- t=0,1,……,N (b) 由(a)可得到：Q N =()()012122121Q p p t t -+-- 由0<p<1，则0<2p<2，-1<2p-1<1，即|2p-1|<1 则21lim =∞→N N Q ，与Q 0取值无关。

第4章无失真信源编码习题及其参考答案4-1 有一信源，它有六个可能的输出，其概率分布如下表所示，表中给出了对应的码A、B、C、D、E和F（1）求这些码中哪些是唯一可译码；（2）求哪些码是及时码；（3）对所有唯一可译码求出其平均码长l。

4-2 设信源61261126()1()()()()iis s sXp sp s p s p sP X=⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦∑。

对此次能源进行m元唯一可译编码，其对应的码长为（l1,l2,…,l6）=(1,1,2,3,2,3)，求m值的最好下限。

（提示：用kraft不等式）4-3设信源为1234567811111111()248163264128128s s s s s s s sXp X⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦，编成这样的码：（000，001，010，011，100，101，110，111）。

求（1）信源的符号熵；（2）这种码的编码效率；（3）相应的仙农码和费诺码。

4-4求概率分布为11122(,,,,)3551515信源的二元霍夫曼编码。

讨论此码对于概率分布为11111(,,,,)55555的信源也是最佳二元码。

4-5有两个信源X和Y如下：121234567()0.200.190.180.170.150.100.01X s s s s s s s p X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦123456789()0.490.140.140.070.070.040.020.020.01Y s s s s s s s s s p Y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦（1）用二元霍夫曼编码、仙农编码以及费诺编码对信源X 和Y 进行编码，并计算其平均码长和编码效率；（2）从X ，Y 两种不同信源来比较三种编码方法的优缺点。

4-6设二元霍夫曼码为（00，01，10，11）和（0，10，110，111），求出可以编得这样 霍夫曼码的信源的所有概率分布。

4-7设信源为12345678()0.40.20.10.10.050.050.050.05X s s s s s s s s p X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦，求其三元霍夫曼编码。