下载文档原格式
可靠性理论第二讲不可修基本系统所谓典型不可修系统是指组成系统的部件失效后并不对其进行维修(更换)的系统。
本讲介绍串联、并联、表决、混联等基本系统的可靠性模型。
描述不可修系统可靠性的主要数值指标是系统可靠度R(t)和系统平均寿命MTTF。
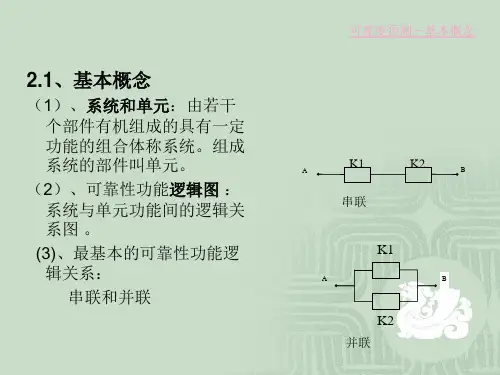
问题：已知部件可靠性，如何求整体（系统）的可靠性？§2.1串联系统串联系统：系统由n个部件组成、n个部件中的任何一个失效均将引起系统失效。
串联系统的可靠性结构框图如图2.1所示。
问题描述：设第i个部件的寿命为X i，可靠度为R i(t)＝p(X i>t)，其中i＝1,2,……,n，并设系统寿命为X，可靠度为R(t)。
假定X1,X2,…,X n相互独立，初始时刻t＝0时所有部件都是新的、且同时开始工作。
由串联系统定义可知，系统寿命X 应等于各部件寿命X i 的最小者，即X =M in {X 1,X 2,……,X n }。
于是，系统的可靠度为：12()()(M {X ,X ,,X })n R t p X t p in t =>=⋅⋅⋅>12(X X X )n p t t t =>>⋅⋅⋅>，，，∏∏===>=ni i n i i t R t X p 11)()( 当第i 个部件的失效率为λi (t )时，系统可靠度为})(ex p{})(ex p{)(0110⎰∑∏⎰==-=-=t n i in i t i du u du u t R λλ ∴系统的失效率为∑=='-=n i i t t R t R t 1)()()()(λλ 因此，一个由独立部件组成的串联系统的失效率是所有部件失效率之和。
系统的平均寿命为：⎰⎰⎰∞∞-==000})(ex p{)(dt du u dt t R MTTF tλ讨论：1）如果t i i e t R λ-=)(，其中i ＝1,2,……,n ，即所有部件寿命X i 服从参数为λi 的负指数分布，那么有：}ex p{)(1∑=-=t i i t t R λ，11][-=∑=ni i MTTF λ 因此，系统的寿命分布也服从负指数分布。
