§7-7 正弦稳态电路功率
- 格式:ppt
- 大小:1.68 MB
- 文档页数:20




正弦稳态电路的瞬时功率与平均功率 - 电工基础图1(a) 表小—个任意的无源二端网络,设端口电压为,电流为,不论电压、电流的波形如何,网络在任一瞬时吸取的功率,即瞬时功率,等于网络端口瞬时电压与瞬时电流的乘积:图 1 任意的无源二端网络( 1 )对于正弦电流电路而言,电压与电流是同频率的正弦时间函数,但在相角上,一般有所区分。
设则 ( 2 )式中为电路输入端电压超前于电流的相角差,即电路的等效阻抗的隔角。
二端网络吸取的平均功率 (average power)( 简称功率 ) 等于上述瞬时功率在—周期内的平均值,故平均功率或 ( 3 )如前所述,式中认为二端网络输入端电压超前于电流的相角,即二端网络端口等效阻抗的辐角。
式〔 3) 表明,二端网络吸取的平均功率等于它所吸取的瞬购功率的伤定重量,当己知一端网络端口电压和电流的存放值 ( 或幅值 ) 以及电压超前十电流的相角时,即可按式 (6—7—3) 计算二端网络吸取的平均功率。
对于正弦电流电路中的电感元件或电容元件来说,由于端口电压与电流间的相角差为,即元件吸取的平均功率 ( 4 ) 即无论电压幅值及电流幅值多大,电感元件与电容元件吸取的平均功率恒等于零。
但瞬时功率却并非恒等于零。
依据式 (2) 可得( 5 )即瞬时功率 P(t) 仅含简谐重量、其值可正可负:这表明,虽然就任一瞬时来看,电感元件与电容元件或是从电源获得能量,或是将能量反送回电源,但在任—周期内,元件获得的总能量等于它释放出的总能量。
这正是由佬能元件只能储存能量而不能消耗能量的特性所打算的。
对于正弦电流电路中的电阻元件来说,由于端口电压与电流同相,即元件吸取的平均功率 ( 6 )而其瞬时功率( 7 )这表明。
不仅电阻元件吸取的平均功率恒为正值,而且它在任何瞬时吸取的瞬时功率也个可能成为负值。
这正是由线性正值电阻元件只能消耗能量间不行能释放能量的特性所打算的。

cos t ω无源网络(1cos2φ+第一种分解形式()()cos cos 2p t UI φt φω=+-⎡⎤⎣⎦UI cos j 恒定分量UI cos (2ωt -j )为正弦分量ωtiOu p (t )∙p 有时为正,有时为负;∙p >0,电路吸收功率;∙p <0,电路发出功率;ωtOp(2)平均功率(有功功率)P第 2 页第二种分解形式:()()cos 1+cos2sin sin 2p t UI φt UI tωj ω=+UI cos j (1+cos2ωt )≥0为不可逆分量UI sin j sin2ωt 为可逆分量ωto能量在电源和一端口之间来回交换(3)无功功率Q可逆分量的最大值定义为无功功率sin Q UI φ=单位:var (乏)Q >0,表示网络吸收无功功率Q <0,表示网络发出无功功率无功功率第 4 页有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)(4)R 、L 、C 元件及阻抗Z 的有功功率和无功功率P R =UI cos j =UI cos0︒=UI =I 2R =U 2/R Q R =UI sin j =UI sin0︒=0P L =UI cos j =UI cos90︒=0Q L =UI sin j =UI sin90︒=UI=I 2X LP C =UI cos j =UI cos(-90︒)=0Q C =UI sin j =UI sin (-90︒)= -UI=I 2X Cu i R+-i u C+-i u L+-电感的无功功率>0吸收无功电容的无功功率<0发出无功第 5 页u i Z+-P Z =UI cos j Q Z =UI sin j 2L L 2C C 00Q I X Q I X ⎧=>⎪⎨=<⎪⎩=I |Z|I cos j =I 2|Z|cos j =I 2R =I |Z |I sin j =I 2|Z |sin j =I 2X=I 2(X L +X C )=Q L +Q C发出无功吸收无功电感和电容具有无功互相补偿的作用第 6 页以感性负载为例R cos P UI U I j ==G cos P UI φUI ==jIUBI GI X sin Q UI U Ij ==Bsin Q UI φUI ==RX +_+_+_U RU XU I GB+_GI IBI U jIURU XU XU 电压的无功分量RU 电压的有功分量GI 电流的有功分量BI 电流的无功分量(3)电压、电流三角形第8 页R P U I =GP UI =X Q U I=BQ UI =jSPQj⎥Z ⎪RX相似三角形jII GI BjUU RU XRX +_+_+_U RU XU I GB+_GI I BI U P =I 2RQ =I 2XRX +_+_+_U RU XU I第9 页3、复功率*S UI= U I负载+_定义:()u iS UI j j =∠- *S UI = 也可表示为:**()S UI U UY ==j P Q =+cos j sin UI φUI φ=+UI φS φ=∠=∠2ZI=有功功率无功功率视在功率*ZII = ***2UU Y Y U == 复数第10 页有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)()R L C P P Q Q Q =∑⎧⎨=+∑⎩总总视在功率不守恒=+j S P Q 总总总()R L C j P Q Q =++∑∑()RL C j P Q Q ⎡⎤=++∑⎣⎦=S ∑ =S S∑ 总复功率守恒无功功率守恒有功功率守恒=S S∑总第11 页求电流源发出的复功率o o 100 236(37.1)VU Z =∠⨯=∠- 例题解法1()()o10j25//5j1523.6(37.1)Z =+-=∠-W()*o o 236(37.1)100 1.88j1.42 kVAS UI ==∠-⨯∠=- +_U 10∠0oA10W j25W5W -j15W第12 页o o 100 236(37.1)VU Z =∠⨯=∠- 解法2()()o10j25//5j1523.6(37.1)Z =+-=∠-W23610 2.36 kVAS UI ==⨯≈+_U 10∠0oA10W j25W5W -j15W()o 2.36(37.1) 1.88j1.42 kVAS =∠-=- 第13 页21I Z =+_+ A_= 8.77* AW V+_D I30⨯4、功率因数的提高设备容量S (额定)向负载送多少有功由负载的阻抗角决定。

正弦稳态电路的功率公式在电路中,功率是电能转换的重要指标之一。
而对于正弦稳态电路,我们可以通过一条简单而有效的公式来计算其功率。
本文将详细介绍正弦稳态电路的功率公式,并解释其背后的原理和应用。
一、正弦稳态电路的功率公式正弦稳态电路是指电路中的电流和电压都是正弦波形式,并且其频率保持不变。
在这种情况下,我们可以使用以下功率公式来计算电路中的功率:P = Vrms * Irms * cos(θ)其中,P表示电路的功率,Vrms表示电压的有效值,Irms表示电流的有效值,θ表示电压和电流之间的相位差。
二、功率公式的原理解释为了更好地理解功率公式的原理,我们可以从电能转换的角度来解释。
在正弦稳态电路中,电流和电压都是周期性变化的,而功率则是电能转化的速率。
根据能量守恒定律,电路中产生的功率等于电能的消耗速率。
在公式中,Vrms和Irms分别表示电压和电流的有效值。
有效值是指在一个周期内,电压和电流的平方值的平均值的平方根。
有效值可以反映电压和电流的实际大小,而不受正弦波形式的影响。
而c os(θ)则表示电压和电流之间的相位差。
相位差是指电压和电流的波形之间的时间差,它可以是正值、负值或零值。
当相位差为零时,电压和电流完全同相,功率取得最大值。
当相位差为正值或负值时,电压和电流存在一定的错位,功率将减小。
因此,正弦稳态电路的功率公式可以通过电压和电流的有效值以及它们之间的相位差来计算电路的功率。
三、功率公式的应用功率公式在电路分析和设计中有着广泛的应用。
它可以帮助我们计算电路中的功率消耗,并进一步优化电路的设计。
功率公式可以用于计算电路中不同元件的功率消耗。
例如,我们可以通过测量电压和电流的有效值,并计算它们之间的相位差,来确定电阻、电容或电感元件的功率消耗。
功率公式可以用于分析电路中的功率传递和传输效率。
通过计算电路中不同节点的功率,我们可以了解能量在电路中的分布情况,找出能量损失的原因,并进一步改进电路的效率。

今日作业:7-117-137.3 正弦稳态电路中的功率Power in Sinusoidal Steady State一、瞬时功率(Instantaneous Power)----W二、平均功率(Average Power or Active Power)----W 三、无功功率(Reactive Power)----Var 四、视在功率(Apparent Power)----VA 五、功率因数(Power Factor )的提高六、复功率(Complex Power)----VA7.3 正弦稳态电路中的功率Power in Sinusoidal Steady State正弦稳态电路+_ui一、瞬时功率(Instantaneous Power)----WA)cos(2V cos 2ϕωω−==t I i t U u 设:tUI t UI t t UI t UI t t UI ui p ωϕωϕϕϕωϕωϕϕωϕωω2sin sin ]2cos 1[cos ]cos sin 2sin cos 2[cos )cos )2[cos()cos(cos 2⋅++=+⋅+⋅=+−=−⋅==ωti,u,p[cos(2)cos )cos [1cos 2]sin sin 2p UI t UI t UI tωϕϕϕωϕω=−+=++⋅ϕcos UI 不可逆部分可逆部分返回二、平均功率(Average Power or Active Power)----Wϕcos )(10UI dtt p T P T==∫cos ϕ−−功率因数正弦稳态电路+_U I计算平均功率的两种方法ϕcos )()(UI P P P R=∑=21RXtg iu 121−=−=ϕψψϕϕ)()的求解:(返回三、无功功率(Reactive Power)----Var sin Q UI ϕ=计算无功功率的另一种方法XQ Q =∑返回正弦稳态电路+_U I 四、视在功率(Apparent Power)----VA22S P Q UI=+=PQSϕ功率三角形注:在工程上视在功率用来表示电源设备(变压器、发电机等)的容量,也可用来衡量发电机可能提供的最大平均功率(额定电压×额定电流)正弦稳态电路+_U I等于多少?问:此电路的功率因数,另一个负载的,,已知一个负载的)(.cos )(.cos 0850Kw 90070Kw 70222111>==<==ϕϕϕϕP P P 1cos ϕ1P 2cos ϕ21I 2I I+_U解例1问题的提出:日常生活中绝大部分负载为感性cos ϕI当U 、P 一定时,∴五、功率因数(Power Factor )的提高P =P R =UI cos ϕ其消耗的有功功率为:R LR U LU IU +-+-+-1、线路损耗增加;2、终端负载工作电压降低,影响其正常工作;3、电源容量增加。

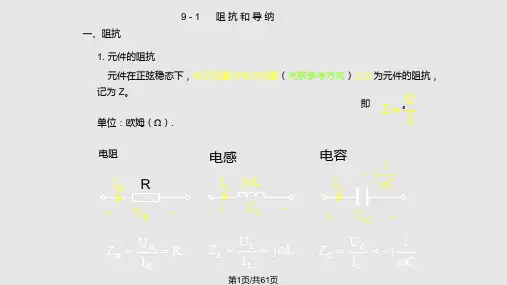


§7-3正弦稳态电路的功率一.瞬时功率如图所示的任意一端口电路N 0,在端口的电压u 与电流i 的参考方向对电路内部关联下,其吸收瞬时功率()()()p t u t i t =⋅若设正弦稳态一端口电路的正弦电压和电流分别为()2cos u t U t ω= ()2cos()i t I t ωϕ=-式中u 0ψ=为正弦电压的初相位,i ψϕ=-为正弦电流的初相位,Z u i ψψψϕ=-=为端口上电压与电流的相位差。
则在某瞬时输入该正弦稳态一端口电路的瞬时功率为则()2cos 2cos()p t U t I t ωωϕ=⋅-[]cos cos(2)UI t ϕωϕ=+- cos cos(2)UI UI t ϕωϕ=+- 常量 两倍于原频率的正弦量cos cos 2cos sin 2sin UI UI t UI t ϕωϕωϕ=++ cos (1cos 2)sin 2sin UI t UI t ϕωωϕ=++ 不可逆部分R ()P t (0)≥ 可逆部分X ()P tN 0 i (t ) u (t ) +_二.平均功率T01()cos TPp t dt UI ϕ=⎰ 可见:1. P 是一个常量,由有效值U 、I 及cos ϕ,u i ()ϕψψ=-三者乘积确定,量纲:W2. 当P >0时,表示该一端口电路吸收平均功率P ;当P <0时,表示该一端口电路发出平均功率|P |。
3. 单一无源元件的平均功率:R P UI =,L C 0,0P P ==。
0900900P ϕϕ⎫<<>⎬<<⎭感性容性-,始终消耗功率。
三.无功功率正弦稳态一端口电路内部与外部能量交换的最大速率(即瞬时功率可逆部分的振幅)定义为无功功率Q ,即 sin QUI ϕ可见:1. Q 也是一个常量,由U 、I 及sin ϕ三者乘积确定,量纲:乏(Var)2. R L C 0,,Q Q UI Q UI ===- 0900Q ϕ<<> 吸收无功功率 9000Q ϕ-<<< 发出无功功率四.视在功率(表观功率)S UI ,反映电源设备的容量(可能输出的最大平均功率),量纲:伏安(V A )。