下载文档原格式
目录1 引言1．1 选题的依据及意义·························································································（1）1．2 国内外研究概况及发展趋势··········································································（2）1．3 论文主要工作·······························································································（3）2 曲柄（导杆）滑块机构简介····································································（4）3 曲柄（导杆）滑块机构的运动学分析3．1 曲柄导杆滑块机构的运动分析······································································（5）3．1．1 机构装配的条件····················································································（6）3．1．2 建立数学模型·························································································（6）3．1．3 计算机辅助分析及其程序设计······························································（9）3. 2曲柄滑块机构的运动分析3．2．1 机构装配的条件·····················································································（25）3．2．2 建立数学模型·······················································································（25）3．2．3 计算机辅助分析及其程序设计·····························································（27）4 曲柄（导杆）滑块机构实验台装置设计4. 1 实验台结构·································································································（40）4.2 实验台硬件操作说明···················································································（41）4.3 用SolidWorks 2006实现实验台的立体图形················································（42）总结·········································································································（46）参考文献·········································································································（47）致谢·········································································································（48）1 引言1．1 选题的依据及意义1．曲柄（导杆）滑块机构定义曲柄滑块机构是铰链四杆机构的演化形式,由若干刚性构件用低副(回转副、移动副)联接而成的一种机构。
% 转动导杆机构运动分析% 已知条件n=200;omega_1=pi*n/30; % 主动件导杆转速和角速度(rad/s)lambda=0.5; % 机构尺度系数alpha_p=45; % 机构许用压力角du=180/pi;hd=pi/180; % 角度与弧度转换系数disp ' ******** 已知条件********'fprintf (' 导杆转速n = %3.4f r/min \n',n)fprintf (' 导杆角速度omega_1 = %3.4f rad/s \n',omega_1)fprintf (' 机构尺度系数lambda = %3.4f \n',lambda)fprintf ('机构许用压力角alpha_p = %3.4f °\n',alpha_p)% 1-计算机构运动参数for phi_1=1:360phi_3(phi_1)=phi_1-asin(lambda*sin(phi_1*hd))*du; % 从动件曲柄角位移omega_3_z=lambda*cos(phi_1*hd);omega_3_m=sqrt(1-lambda^2*sin(phi_1*hd)^2);omega_3(phi_1)=omega_1*(1-omega_3_z/omega_3_m); % 从动件曲柄角速度i_31(phi_1)=omega_3(phi_1)/omega_1; % 机构传动比alpha(phi_1)=asin(lambda*sin(phi_1*hd))*du; % 机构压力角enddisp ' 'disp ' *** 转动导杆机构的运动参数***'disp ' 导杆转角曲柄角位移曲柄角速度'disp ' (°) (°) (rad/s) 'for phi_1=10:10:360ydcs=[phi_1 phi_3(phi_1) omega_3(phi_1)];disp(ydcs)end% 2-绘制机构的运动线图figure(1);subplot(2,1,1) % 曲柄角位移线图phi_1=1:360;plot(phi_1,phi_3);xlabel ('导杆转角\it \phi_1 / \rm( °)')ylabel ('\it \phi_3 / \rm(°)')title('从动件曲柄角位移线图');subplot(2,1,2) % 曲柄角速度线图phi_1=1:360;plot(phi_1,omega_3);xlabel ('导杆转角\it \phi_1 / \rm( °)')ylabel ('\it \omega_3 / \rm(rad/s)')title('从动件曲柄角速度线图');% 3-绘制机构的压力角线图figure(2);phi_1=1:360;plot(phi_1,alpha);xlabel ('导杆转角\it \phi_1 / \rm( °)');ylabel ('\it \alpha / \rm(°)');line([0,360],[alpha_p,alpha_p]);text(365,45,'\alpha_{max}=45°');line([0,360],[0,0]); % 横坐标line([0,360],[-alpha_p,-alpha_p]);text(365,-45,'\alpha_{min}=-45°');title('机构压力角线图');text(230,30,'可行域');% 4-绘制机构的传动比线图和传动比与尺度系数关系线图figure(3);subplot(1,2,1) % 机构传动比线图phi_1=1:360;plot(phi_1,i_31);xlabel ('导杆转角\it \phi_1 / \rm( °)')ylabel ('\it i_{31}')title('机构传动比线图(尺度系数是定值)');subplot(1,2,2) % 机构传动比与尺度系数关系线图line([0,sin(alpha_p*hd)],[1,1+sin(alpha_p*hd)]);line([0,sin(alpha_p*hd)],[1,1-sin(alpha_p*hd)]);line([sin(alpha_p*hd),sin(alpha_p*hd)],[1+sin(alpha_p*hd),1-sin(alpha_p*hd)]); xlabel ('尺度系数\it \lambda = e / l_3 ')ylabel ('\it i_{31}')title('传动比与尺度系数关系线图');text(0.25,1.4,'\it i_{31max}')text(0.32,1.0,'可行域')text(0.25,0.6,'\it i_{31min}')******** 已知条件********导杆转速n = 200.0000 r/min导杆角速度omega_1 = 20.9440 rad/s机构尺度系数lambda = 0.5000机构许用压力角alpha_p = 45.0000 °*** 转动导杆机构的运动参数***导杆转角曲柄角位移曲柄角速度(°) (°) (rad/s)10.0000 5.0191 10.592020.0000 10.1534 10.956430.0000 15.5225 11.577540.0000 21.2528 12.472550.0000 27.4790 13.657060.0000 34.3411 15.135170.0000 41.9757 16.886680.0000 50.5013 18.854790.0000 60.0000 20.9440100.0000 70.5013 23.0332 110.0000 81.9757 25.0013 120.0000 94.3411 26.7528 130.0000 107.4790 28.2309 140.0000 121.2528 29.4154 150.0000 135.5225 30.3104 160.0000 150.1534 30.9315 170.0000 165.0191 31.2959 180.0000 180.0000 31.4159 190.0000 194.9809 31.2959 200.0000 209.8466 30.9315 210.0000 224.4775 30.3104 220.0000 238.7472 29.4154 230.0000 252.5210 28.2309 240.0000 265.6589 26.7528 250.0000 278.0243 25.0013 260.0000 289.4987 23.0332 270.0000 300.0000 20.9440 280.0000 309.4987 18.8547 290.0000 318.0243 16.8866 300.0000 325.6589 15.1351 310.0000 332.5210 13.6570 320.0000 338.7472 12.4725 330.0000 344.4775 11.5775 340.0000 349.8466 10.9564 350.0000 354.9809 10.5920 360.0000 360.0000 10.4720。
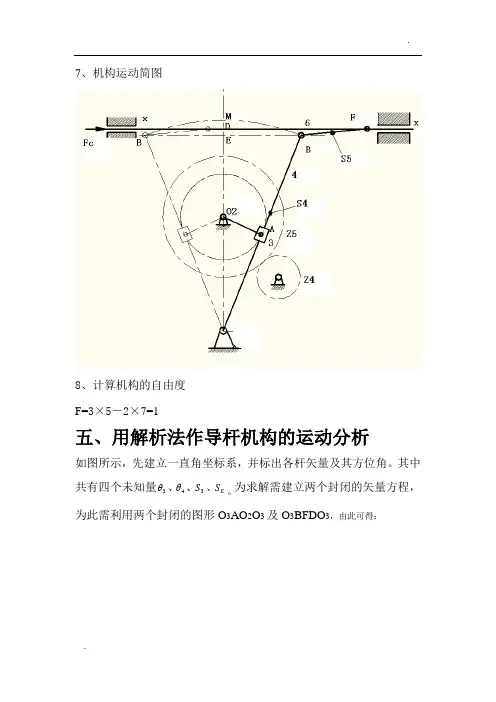
7、机构运动简图8、计算机构的自由度 F=3×5－2×7=1五、用解析法作导杆机构的运动分析如图所示，先建立一直角坐标系，并标出各杆矢量及其方位角。
其中共有四个未知量3θ、4θ、3S 、E S 。
为求解需建立两个封闭的矢量方程，为此需利用两个封闭的图形O 3AO 2O 3及O 3BFDO 3，由此可得：→→→→→→→+=+=+ES L L '64L3S3L1L6并写成投影方程为：’64433E 4433116331133L sin L sin L 0S cos L cos L sin sin cos cos =+=-++==θθθθθθθθL L S L S由上述各式可解得：4433E 311343364111163cos L cos L S cos cos L S L sin L L arcsincos L sin L L arctanθθθθθθθθθ⨯+⨯=⨯=⨯-=⨯⨯+=⋅由以上各式即可求得3θ、4θ、3S 、E S 四个运动变量，而滑块的方位角2θ=3θ。
然后，分别将上式对时间取一次、二次导数，并写成矩阵形式，及得一下速度和加速度方程式。
⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡//-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-•00cos sin S 0cos L cos L 01sin L -sin L -000cos S sin 00sin S -cos 111114334433443333333θθθθθθθθθθL L w v w w E =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-••E αααθθθθθθθθ43344334433333333S 0cos L cos L 01sin L -sin L -000cos S sin 00sin S -cos ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡//-+⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡---••00sin cos 0sin w L -s w L -00c w L -cos w L -000sin w S -cos cos 00cos w S sin S -sin 111111144433344433333333333333333θθθθθθθθθθθθw L w L w in os S w w 而2w =3w 、2α=3α根据以上各式，将已知参数代入，即可应用计算机计算。
PPT1 本次课讲授导杆机构应用
PPT2 本次课的教学目标是,了解导杆机构应用的实例
PPT３１．摆动导杆机构请注意看动画运动情况
１）结构组成：是由机架曲柄摇杆（导杆）滑套（滑块）组成
２）工作原理：曲柄作定轴匀速转动，带动滑套（滑块）转动并摆动，滑套（滑块）套在导杆上，使导杆往复来回摆动。
PPT４２．摆动导杆机构应用实例
１）摆动导杆机构在插床上的应用请注意看动画运动情况,工作原理为
ＡＢ构件绕销轴Ａ作定轴转动，带动滑块Ｂ转动并摆动，滑块Ｂ在导杆ＣＤ上滑动,并带动导杆ＣＤ绕销轴Ｃ做定轴摆动，摆杆ＣＤ带动连杆ＤＥ做平面运动，连杆ＤＥ带动滑块Ｅ和刀架及插刀做往复运动，实现插削加工。
PPT4 ２）摆动导杆机构在牛头刨床上的应用请注意看动画运动情况
构件２绕铰链Ｂ作定轴转动，带动滑块３一起转动，滑块３绕铰链Ｃ摆动，并沿导杆ＤＡ滑动，带动导杆ＤＡ绕固定铰链Ａ摆动，连杆ＤＥ做平面运动，滑块Ｅ沿ＦＥ导杆上下滑动，并带动刨床的滑枕做水平往复移动，从而实现刨刀的切削加工。
PPT５下面对本次课内容进行小结：本次课，
１．摆动导杆机构１）结构组成２）工作原理
２．摆动导杆机构应用实例
１）摆动导杆机构在插床上的应用
２）摆动导杆机构在牛头刨床上的应用
PPT６本次课作业：选择题图示牛头刨床机构的导杆为。
Ａ．构件ＡＤＢ．构件ＢＣＣ．构件ＤＥ。
《机械设计基础》第五版摆动导杆机构设计课件
摆动导杆机构是一种用来传递动力和运动的机构。
在机械设计中，摆动导杆机构是经常用来设计滑块机构和曲柄机构的重要组成部分。
摆动导杆机构通常由下面几个部分组成：
1.导杆：导杆是机构的最主要的构成部分，通常由一条杆件构成，其作用是引导滑块或连杆的运动。
2.摆杆：摆杆是导杆机构的另一个重要部分，通常被用来连接导杆和其他部分。
摆杆的长度和角度通常被用来影响机构的运动状态。
3.滑块：滑块是机构中一个常用的部分，通常被用来将动力从曲柄传递给导杆，进而让导杆带动滑块和其他部分的运动。
4.曲柄：曲柄是机构的主要动力来源之一，通常被用来提供旋转动力，用来带动其他部分的运动。
设计摆动导杆机构需要考虑以下几个方面：
1.机构的应用场景和需要：设计摆动导杆机构需要首先考虑机构应用的场景和需要，例如机构所需要承受的载荷大小、运动速度要求等。
2.机构的运动状态和限制：设计摆动导杆机构需要考虑机构的运动状态和限制，例如机构是否需要进行平移或者旋转等，以及机构是否有特殊的运动限制或者要求。
3.材料和制造工艺：设计摆动导杆机构需要选择适合的材料和制造工艺，以保证机构的可靠性和耐用性。
4.机构的结构和尺寸：设计摆动导杆机构需要考虑机构的结构和尺寸，以保证机构的可操作性和可维护性。
总的来说，摆动导杆机构的设计需要综合考虑机械设计基础知识、应用场景和运动要求等方面，以达到机构可靠、高效、稳定的运行状态。
三、设计内容1、导杆机构运动分析选择表1-1中方案II设计内容导杆机构的运动分析导杆机构的动态静力分析符号n2 L0204 L02A L04B L BC L04S4 X S6 Y S6 G4 G6 P Y P J S4 单位r/min mm N mm kgm2方案Ⅰ60 380 110 540 0.25L04B0.5L04B240 50 200 700 7000 80 1.1 Ⅱ64 350 90 580 0.3L04B0.5L04B200 50 220 800 9000 80 1.2 Ⅲ72 430 110 810 0.36L04B0.5L04B180 40 220 620 8000 100 1.2表1-11、机构运动简图。
图1-12、曲柄位置“7”速度分析，加速度分析（列矢量方程，画速度图，加速度图）取曲柄位置“7”进行速度分析，其分析过程同曲柄位置“1”。
取构件3和4的重合点A进行速度分析。
列速度矢量方程，得υA4=υA3+υA4A3大小? √?方向⊥O4A⊥O2A∥O4B代表pa4 pa3 a3a4V A3=ω2l o2A=64/60×6.28×0.09=0.603m/s取速度极点P，速度比例尺µv=0.01(m/s)/mm，作速度多边形如图1-2则由图1-2知，υA4=pa4·μv=29×0.01=0.29m/sυA4A3=a3a4·μv=52×0.01m/s=0.52m/s图1-2υB5=υB4=υA4·O4B/ O4A=0.44m/s取5构件为研究对象，列速度矢量方程，得υC5=υB5+υC5B5大小? √?方向∥XX⊥O4B⊥BC代表pc5 pb4 b4b5其速度多边形如图1-2所示，有υC5=5Pc·μv=42×0.01=0.42m/s取曲柄位置“7”进行加速度分析，取曲柄构件3和4的重合点A进行加速度分析.列加速度矢量方程,得:a A4 =a A4n +a A4t= a A3n +a A4A3k+a A4A3r 大小? ω42l O4A ?√2ω4υA4A3 ? 方向? A→O4⊥O4B A→O2⊥O4B（向右）∥O4B代表pA4’pn4’n4’A4’p’A3’A3’k’k’A4’取加速度极点为P＇,加速度比例尺μa=0.02（m/s2）/mm作加速度多边形图1-3图1-3则由图1─3知:a A4t= n4’A4’·μa =137×0.02m/s2=2.74m/s2α4= a A4t/l O4A = 7.17 m/s2a A4 = pA4’·μa = 138×0.01m/s2 =2.76 m/s2用加速度影象法求得a B5 = a B4 = a A4 ×l O4B/l O4A=4.19m/s2取5构件的研究对象，列加速度矢量方程，得a C5=a B5+ a C5B5n+ a C5B5t大小?√√?方向∥xx √ C→B ⊥BC代表 P’c5’ P’B5’ n5’B5’ C5’n5’加速度比例尺μa=0.02（m/s2）/mm其加速度多边形如图1─4所示，有图1-4a C5B5t= n5’c5’·μa =31×0.02m/s2 =0.62m/s2a C5 = P’c5’·μa =179×0.02m/s2 =3.58m/s23、曲柄位置“10”速度分析，加速度分析（列矢量方程，画速度图，加速度图）取曲柄位置“10”进行速度分析。
取构件3和4的重合点A进行速度分析。
列速度矢量方程，得υA4=υA3+υA4A3大小? √?方向⊥O4A⊥O2A∥O4B代表 pa4 pa a a3a4V A3=ω2l o2A=64/60×6.28×0.11=0.6908m/s取速度极点P，速度比例尺µv=0.01(m/s)/mm，作速度多边形如图1-5。
图1-5则由图1-5知，υA4=pa4·μv=52.8516×0.01=0.528516m/sυA4A3=a3a4·μv=78.4778×0.01m/s=0.784778m/sυB5=υB4=υA4·O4B/ O4A=0.2007m/s.取5构件为研究对象，列速度矢量方程，得υC5=υB5+υC5B5大小? √?方向∥XX⊥O4B⊥BC代表pc pb5b5c其速度多边形如图1-5所示，有υC5=pc·μv=100.3953×0.01=1.003953 m/sυC5B5=b5c.μv=57.2909×0.01=0.572909 m/s取曲柄位置“10”进行加速度分析，取曲柄构件3和4的重合点A 进行加速度分析.列加速度矢量方程,得a A4 = a A4n + a A4t = a A3n + a A4A3k + a A4A3r大小? ω42l O4A ? √ 2ω4υA4 A3 ?方向 ? A →O 4 ⊥O 4B A →O 2 ⊥O 4B （向左） ∥O 4B代表 p ’A 4’ p ’A t ’ A t ’A 4’ p ’A 3’ A 3’k ’ k ’A 4’取加速度极点为P ＇,加速度比例尺μa =0.02（m/s 2）/mm 作加速度多边形图1-6则由图1─6知:a A4n=p ’A t ’ =)264.0/56.0(2×0.264m/s 2=1.187m/s 2a A4t =96×0.02＝1.82m/sa A4 = p ’A 4’·μa = 94×0.02m/s 2 =1.88 m/s 2a A4A3k =2ω4υA4 A3 =0.848 m/s 2用加速度影象法求得a B5 = a B4 = a A4 ×l O4B /l O4A =4.13 m/s 2取5构件的研究对象，列加速度矢量方程，得a C5= a B5+ a C5B5n + a C5B5t大小 ? √ √ ?方向 ∥xx √ C →B ⊥BC代表 p ’C 5’ p ’B 5’ B 5’B 5t ’ B 5t ’C 5’ 速度比例尺µa =0.1(m/s2)/mm 其加速度多边形如图1─6所示，有a C5 = p´C5·μa=175×0.02m/s 2 =3.5m/s 2图1-62、机构运态静力分析导杆机构的动态静力分析已知各构件的重量G（曲柄2、滑块3和连杆5的重量都可忽略不计），导杆4绕重心的转动惯量Js4及切削力F P的变化规律。
要求求各运动副中反作用力及曲柄上所需要的平衡力矩。
取“7”点为研究对象，分离5、6构件进行运动静力分析，作阻力体如图1─7所示。
图1—7已知P=-9000N，G6=800N，又a c=a c5=3.58m/s2,那么我们可以计算F S6=- G6/g×a c =-800/10×-3.58=286.4N又ΣF=P+G6+F S6+F p45+F R16=0,作为多边行如图1-8所示，µN=50N/mm。
图1-8由图1-7力多边形可得：F R45=-aF R45·µN=-173.7×50N=-8685NF R16= F S6 F R16·µN=24×50N=1200N对c点取距，有ΣM C=-P·y P-G6X S6+ F R16·x-F S6·y S6=0代入数据得x=62.6mm分离3,4构件进行运动静力分析，杆组力体图如图1-8所示，已知：F R54=-F R45=8685N G4=220Na S4=a A4·l O4S4/l O4A=2.6×290/380m/s2=1.98m/s2αS4=α4´=6.57rad/s2由此可得：F S4=-G4/g×a S4 =-220/10×1.98N=-43.56NM S4=-J S4·αS4=-1.2×6.57N·m= -7.88N·m在图1-9中，对A点取矩得：ΣM O4=8685×0.146-7.87-220×0.016=0.97×F R32ΣM O4=8685×0.146-7.87-220×0.016=0.97×F R32代入数据，F R23=F O4τF R32·µN=12500得F O4τ=-4050N由h1=M S/F S4代入数据得h1=182mmF S4'=F S4·l o4s4' /l o4s4=-43.56×472/290N=70.2N图1-9又ΣF=F R54+F R32+F S4'+G4+F O4n+F O4τ=0,作力的多边形如图1-10所示，µN=50N/mm。
图1-10由图1-10可得：F O4τ=a F O4τ·µN=81×50=4050NF O4n=aF O4n·µN=16×50N·= 800N对曲柄2进行运动静力分析，作组力体图如图1-11所示，图1-11µL=1mm/mm.由图1-11可知，h2=11mm,则，对曲柄列平行方程有，ΣM O2=M2-F R23·h2=0即M-12500×0.101=0，即M=138N·M3、求刨头的位移，速度和加速度曲线位移与时间，速度与时间，加速度与时间曲线。
图1-12由以上三条曲线，位移与时间，速度与施加，加速度与时间曲线，可以看出牛头刨床的运行过程，c点的运动情况。
