一般线性回归模型

logistic回归模型的一般形式
logistic回归模型是一种广义的线性回归分析模型，常用于数据挖掘、疾病自动诊断、经济预测等领域。

其一般形式可表达为：logit(p) = α+β1*X1+β2*X2+β3*X3+.....+βk*Xk。

其中，logit(p)表示Y的对数发生比，p为Y事件发生的概率；α为常数项，βi（i=1，2，3，...，k）为自变量Xi的回归系数。

与传统的线性回归模型不同，logistic 模型中的因变量是分类变量而不是连续变量。

它反映了自变量对因变量的线性影响，常用于探讨引发疾病的危险因素，并根据危险因素预测疾病发生的概率等。

在实际应用中，logistic 回归模型的形式可能会根据具体问题和数据特点进行调整和扩展。

线性统计模型知识点总结一、线性回归模型1. 线性回归模型的基本思想线性回归模型是一种用于建立自变量和因变量之间线性关系的统计模型。

它的基本思想是假设自变量与因变量之间存在线性关系，通过对数据进行拟合和预测，以找到最佳拟合直线来描述这种关系。

2. 线性回归模型的假设线性回归模型有一些假设条件，包括：自变量与因变量之间存在线性关系、误差项服从正态分布、误差项的方差是常数、自变量之间不存在多重共线性等。

3. 线性回归模型的公式线性回归模型可以用如下的数学公式来表示：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε，其中Y 是因变量，X是自变量，β是模型的系数，ε是误差项。

4. 线性回归模型的参数估计线性回归模型的参数估计通常使用最小二乘法来进行。

最小二乘法的目标是通过最小化残差平方和来寻找到最佳的模型系数。

5. 线性回归模型的模型评估线性回归模型的好坏可以通过很多指标来进行评价，如R-squared（R^2）、调整后的R-squared、残差标准差、F统计量等。

6. 线性回归模型的应用线性回归模型广泛应用于经济学、金融学、市场营销、社会科学等领域，用以解释变量之间的关系并进行预测。

二、一般线性模型（GLM）1. 一般线性模型的基本概念一般线性模型是一种用于探索因变量与自变量之间关系的统计模型。

它是线性回归模型的一种推广形式，可以处理更为复杂的数据情况。

2. 一般线性模型的模型构建一般线性模型与线性回归模型相似，只是在因变量和自变量之间的联系上，进行了更为灵活的变化。

除了线性模型，一般线性模型还可以包括对数线性模型、逻辑斯蒂回归模型等。

3. 一般线性模型的假设一般线性模型与线性回归模型一样，也有一些假设条件需要满足，如误差项的正态分布、误差项方差的齐性等。

4. 一般线性模型的模型评估一般线性模型的模型评估通常涉及到对应的似然函数、AIC、BIC、残差分析等指标。

5. 一般线性模型的应用一般线性模型可以应用于各种不同的领域，包括医学、生物学、社会科学等，用以研究因变量与自变量之间的关系。

线性回归模型的经典假定及检验、修正一、线性回归模型的基本假定1、一元线性回归模型一元线性回归模型是最简单的计量经济学模型，在模型中只有一个解释变量，其一般形式是Y =β0+β1X 1+μ其中，Y 为被解释变量，X 为解释变量，β0与β1为待估参数，μ为随机干扰项。

回归分析的主要目的是要通过样本回归函数（模型）尽可能准确地估计总体回归函数（模型）。

为保证函数估计量具有良好的性质，通常对模型提出若干基本假设。

假设1：回归模型是正确设定的。

模型的正确设定主要包括两个方面的内容：（1）模型选择了正确的变量，即未遗漏重要变量，也不含无关变量；（2）模型选择了正确的函数形式，即当被解释变量与解释变量间呈现某种函数形式时，我们所设定的总体回归方程恰为该函数形式。

假设2：解释变量X 是确定性变量，而不是随机变量，在重复抽样中取固定值。

这里假定解释变量为非随机的，可以简化对参数估计性质的讨论。

假设3：解释变量X 在所抽取的样本中具有变异性，而且随着样本容量的无限增加，解释变量X 的样本方差趋于一个非零的有限常数，即∑(X i −X ̅)2n i=1n→Q,n →∞ 在以因果关系为基础的回归分析中，往往就是通过解释变量X 的变化来解释被解释变量Y 的变化的，因此，解释变量X 要有足够的变异性。

对其样本方差的极限为非零有限常数的假设，旨在排除时间序列数据出现持续上升或下降的变量作为解释变量，因为这类数据不仅使大样本统计推断变得无效，而且往往产生伪回归问题。

假设4：随机误差项μ具有给定X 条件下的零均值、同方差以及无序列相关性，即E(μi|X i)=0Var(μi|X i)=σ2Cov(μi,μj|X i,X j)=0, i≠j随机误差项μ的条件零均值假设意味着μ的期望不依赖于X的变化而变化，且总为常数零。

该假设表明μ与X不存在任何形式的相关性，因此该假设成立时也往往称X为外生性解释变量随机误差项μ的条件同方差假设意味着μ的方差不依赖于X的变化而变化，且总为常数σ2。

各种线性回归模型原理线性回归是一种广泛应用于统计学和机器学习领域的方法，用于建立自变量和因变量之间线性关系的模型。

在这里，我将介绍一些常见的线性回归模型及其原理。

1. 简单线性回归模型（Simple Linear Regression）简单线性回归模型是最简单的线性回归模型，用来描述一个自变量和一个因变量之间的线性关系。

模型方程为：Y=α+βX+ε其中，Y是因变量，X是自变量，α是截距，β是斜率，ε是误差。

模型的目标是找到最优的α和β，使得模型的残差平方和最小。

这可以通过最小二乘法来实现，即求解最小化残差平方和的估计值。

2. 多元线性回归模型（Multiple Linear Regression）多元线性回归模型是简单线性回归模型的扩展，用来描述多个自变量和一个因变量之间的线性关系。

模型方程为：Y=α+β1X1+β2X2+...+βnXn+ε其中，Y是因变量，X1,X2,...,Xn是自变量，α是截距，β1,β2,...,βn是自变量的系数，ε是误差。

多元线性回归模型的参数估计同样可以通过最小二乘法来实现，找到使残差平方和最小的系数估计值。

3. 岭回归（Ridge Regression）岭回归是一种用于处理多重共线性问题的线性回归方法。

在多元线性回归中，如果自变量之间存在高度相关性，会导致参数估计不稳定性。

岭回归加入一个正则化项，通过调节正则化参数λ来调整模型的复杂度，从而降低模型的过拟合风险。

模型方程为：Y=α+β1X1+β2X2+...+βnXn+ε+λ∑βi^2其中，λ是正则化参数，∑βi^2是所有参数的平方和。

岭回归通过最小化残差平方和和正则化项之和来估计参数。

当λ=0时，岭回归变为多元线性回归，当λ→∞时，参数估计值将趋近于0。

4. Lasso回归（Lasso Regression）Lasso回归是另一种用于处理多重共线性问题的线性回归方法，与岭回归不同的是，Lasso回归使用L1正则化，可以使得一些参数估计为0，从而实现特征选择。

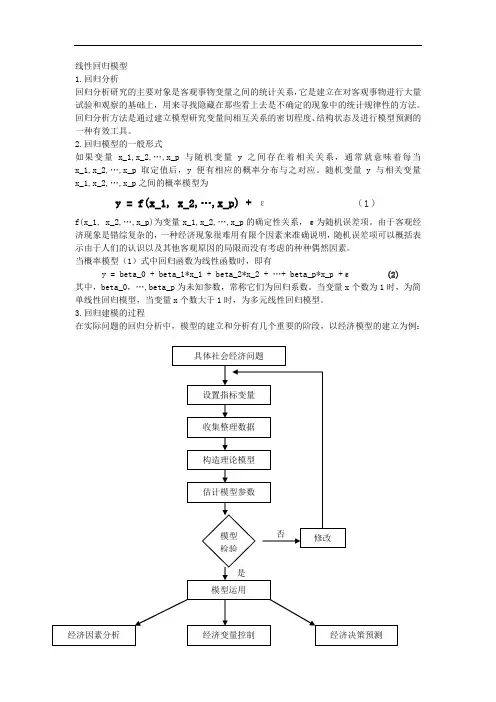
线性回归模型1.回归分析回归分析研究的主要对象是客观事物变量之间的统计关系，它是建立在对客观事物进行大量试验和观察的基础上，用来寻找隐藏在那些看上去是不确定的现象中的统计规律性的方法。

回归分析方法是通过建立模型研究变量间相互关系的密切程度、结构状态及进行模型预测的一种有效工具。

2.回归模型的一般形式如果变量x_1,x_2,…,x_p与随机变量y之间存在着相关关系，通常就意味着每当x_1,x_2,…,x_p取定值后，y便有相应的概率分布与之对应。

随机变量y与相关变量x_1,x_2,…,x_p之间的概率模型为y = f(x_1, x_2,…,x_p) + ε（1）f(x_1, x_2,…,x_p)为变量x_1,x_2,…,x_p的确定性关系，ε为随机误差项。

由于客观经济现象是错综复杂的，一种经济现象很难用有限个因素来准确说明，随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。

当概率模型（1）式中回归函数为线性函数时，即有y = beta_0 + beta_1*x_1 + beta_2*x_2 + …+ beta_p*x_p +ε (2)其中，beta_0，…,beta_p为未知参数，常称它们为回归系数。

当变量x个数为1时，为简单线性回归模型，当变量x个数大于1时，为多元线性回归模型。

3.回归建模的过程在实际问题的回归分析中，模型的建立和分析有几个重要的阶段，以经济模型的建立为例：（1）根据研究的目的设置指标变量回归分析模型主要是揭示事物间相关变量的数量关系。

首先要根据所研究问题的目的设置因变量y，然后再选取与y有关的一些变量作为自变量。

通常情况下，我们希望因变量与自变量之间具有因果关系。

尤其是在研究某种经济活动或经济现象时，必须根据具体的经济现象的研究目的，利用经济学理论，从定性角度来确定某种经济问题中各因素之间的因果关系。

（2）收集、整理统计数据回归模型的建立是基于回归变量的样本统计数据。

一般线性回归分析案例
案例背景：
在本案例中，我们要研究一个公司的运营数据，并探究它们之间的关
联性。

这家公司的运营数据包括：它的营业额（单位：万元）、产品质量
指数（QI）、客户满意度（CSI）和客户数量。

我们的目标是建立营业额
与其他变量之间的关联性模型，来预测公司未来的营业额。

资料收集：
首先，我们需要收集有关营业额、QI、CSI和客户数量的数据，以进
行分析。

从历史记录上可以收集到过去六个月的数据。

数据预处理：
接下来，我们需要对数据进行预处理，可以使用Excel进行格式整理，将数据归类分组，并计算总营业额。

建立模型：
接下来，我们就可以利用SPSS软件来建立一般线性回归模型，模型
表示为：Y=β0+β1X1+β2X2+…+βnXn。

其中，Y代表营业额，X1、
X2…Xn代表QI、CSI和客户数量等因素。

模型检验：
接下，我们要对模型进行检验，确定哪些因素与营业额有关联性，检
验使用R方和显著性检验确定系数的有效性。

各种线性回归模型原理线性回归是一种经典的统计学方法，用于建立自变量和因变量之间的线性关系。

在这个模型中，我们假设自变量和因变量之间存在一个线性函数关系，通过找到最佳的拟合直线，我们可以预测和解释因变量。

在线性回归中，我们通常使用以下三种模型：简单线性回归模型、多元线性回归模型和多项式回归模型。

1.简单线性回归模型：简单线性回归是最基本的线性回归模型。

它用于研究只有一个自变量和一个因变量之间的关系。

假设我们有一个自变量x和对应的因变量y。

简单线性回归模型可以表示为：y=β0+β1*x+ε其中，y是因变量，x是自变量，β0和β1是回归系数，ε是误差项。

我们的目标是找到最佳的回归系数，使得模型对观测数据的拟合最好。

2.多元线性回归模型：当我们需要考虑多个自变量对因变量的影响时，可以使用多元线性回归模型。

多元线性回归模型可以表示为：y = β0 + β1 * x1 + β2 * x2 + ... + βn * xn + ε其中，y是因变量，x1, x2, ..., xn是自变量，β0, β1,β2, ..., βn是回归系数，ε是误差项。

我们通过最小化误差项的平方和来估计回归系数。

3.多项式回归模型：多项式回归模型是在线性回归模型的基础上引入了多项式项的扩展。

在一些情况下，自变量和因变量之间的关系可能不是简单的线性关系，而是复杂的曲线关系。

多项式回归模型可以通过引入自变量的高次幂来建立非线性关系。

例如，二阶多项式回归模型可以表示为：y=β0+β1*x+β2*x^2+ε我们可以使用最小二乘法来估计回归系数，从而找到最佳的拟合曲线。

在以上三种线性回归模型中，我们以最小二乘法作为求解回归系数的方法。

最小二乘法通过最小化观测值与模型拟合值之间的残差平方和来选择最佳的回归系数。

通过最小二乘法，我们可以得到回归系数的闭式解，即可以明确得到回归系数的数值。

除了最小二乘法，还有其他求解回归系数的方法，例如梯度下降法和正规方程法。

线性回归模型
简介
线性回归模型是一种用于预测数值型数据的方法，它的基本思
想是通过对数据进行统计分析和拟合，建立数学模型，来描绘出
变量之间的关系。

该模型还可以帮助我们预测某个变量的数值，
或者找出变量之间的因果关系。

实现
线性回归模型的实现是通过最小二乘法来计算出最佳拟合直线，然后通过这条直线来描述变量之间的关系。

最小二乘法的目的是
使观测数据与拟合直线的差距最小化，从而得到最接近真实数据
的结果。

应用
线性回归模型的应用很广泛，可以应用于很多领域，比如经济学、物理学、社会学、心理学等。

其中，由于数据量较大，经常
会使用Excel或者Python等工具来进行计算和分析。

在经济学领域，线性回归模型通常用来预测商品价格、市场走势等，从而指导投资决策。

在物理学领域，线性回归模型则可以应用于天文学、地震学等领域，帮助解决科学难题。

优缺点
线性回归模型的优点在于它具备精度高、易于解释、计算快、效率高等优点。

同时，该模型还可以处理多元回归问题，进一步拓展了其应用范围。

然而，线性回归模型的缺点也是存在的。

一些因果关系可能并不能依靠线性回归模型来获得，不同的数据可能会造成误差，同时该算法也对异常点很敏感，需要进行筛选。

总结
线性回归模型是一种重要的数据分析方法，它可以帮助我们预测某个变量的数值，或者找出变量之间的因果关系。

在实际的应
用中，我们需要结合自己的实际情况来选择不同的数据分析方法，最大化地发挥统计分析的优势。

线性回归分析方法线性回归是一种常用的统计分析方法，用于研究自变量与因变量之间的线性关系。

本文将介绍线性回归的基本原理、模型假设、参数估计方法以及结果解释等内容，帮助读者更好地理解和应用线性回归分析方法。

一、线性回归的基本原理线性回归假设自变量和因变量之间存在线性关系，通过拟合一个线性方程来描述这种关系。

假设我们有一个因变量Y和一个自变量X，线性回归模型可以表示为：Y = β0 + β1X + ε其中，β0是截距，β1是自变量的回归系数，ε是误差项，表示模型无法完全解释的因素。

线性回归的目标是找到最佳的回归系数，使得预测值与真实值之间的误差最小化。

二、线性回归的模型假设在线性回归分析中，有几个关键的假设前提需要满足：1. 线性关系假设：自变量和因变量之间的关系是线性的。

2. 独立性假设：观测样本之间是相互独立的，误差项之间也是独立的。

3. 同方差性假设：误差项具有相同的方差，即误差项的方差在不同的自变量取值下是恒定的。

4. 正态性假设：误差项服从正态分布。

如果以上假设不满足，可能会导致线性回归分析的结果不可靠。

三、线性回归的参数估计方法线性回归的参数估计方法通常使用最小二乘法（Ordinary Least Squares, OLS）来确定回归系数。

最小二乘法的思想是通过最小化观测值与估计值之间的残差平方和来拟合回归模型。

具体而言，我们可以通过以下步骤来估计回归系数：1. 计算自变量X和因变量Y的均值。

2. 计算自变量X和因变量Y与其均值的差。

3. 计算X与Y的差乘积的均值。

4. 计算X的差的平方的均值。

5. 计算回归系数β1和β0。

四、线性回归模型的结果解释线性回归模型的结果可以用来解释自变量对因变量的影响程度以及回归系数的显著性。

通常我们会关注以下几个指标：1. 回归系数：回归系数β1表示自变量X单位变化时，因变量Y的平均变化量。

回归系数β0表示当自变量X为零时，因变量Y的平均值。

2. R平方：R平方是衡量模型拟合优度的指标，它表示因变量Y的变异中有多少百分比可以由自变量X来解释。