材料力学课件
- 格式:doc
- 大小:727.50 KB
- 文档页数:15










1绪论1.1可变形固体的几个基本假设连续性假设——物体在整个体积内是密实的,无间隙2.均匀性假设——任取一点可代替整体理想弹性体 3.各向同性假设——材料沿各个方向的力学性能相同线弹性 4.弹性范围内假设——变形体在外力作用下产生形变,外力卸除后能完全恢复的那部分形变5.小变形假设——尺寸和形状的改变在可接受范围内1.2材料力学主要研究对象杆纵向尺寸比横向尺寸大得多的构件。
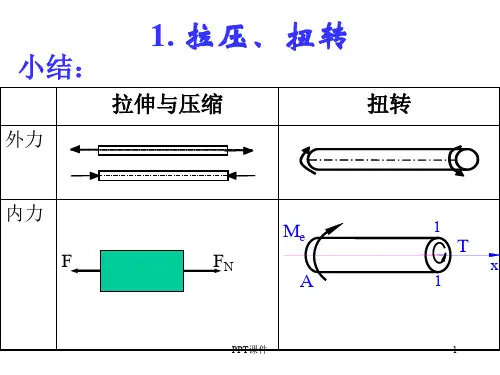
正应力σ强度→应力切应力τ轴向拉伸或轴向压缩变形剪切变形纯弯曲:只有一对力偶作用刚度→变形弯曲变形纯弯曲横力弯曲:例如,梁在横力作用下的变形扭转变形剪切稳定性→保证构件在破坏之前不失效工程中很少有构件只有一种基本变形的,都是属于组合形式。
所以要先了解每一种基本变形,然后再分析组合变形。
2轴向拉伸和压缩2.1材料的力学性能(拉、压)塑性材料:低碳钢力学性能——在外力作用下材料在变形和破坏方面所表现出来的特性脆性材料:铸铁2.1.1低碳钢的拉伸曲线① 在弹性阶段ob 内,a 点对应的应力称为材料的比例极限σp ,是应力应变符合胡克定律的最高限,即变形为线弹性;而从a 到b 变形仍是弹性的,只不过非线性,撤销外力后,变形可完全恢复。
若超过b 点弹性极限σe ,卸载后变形不可完全恢复,有部分塑性变形留下来。
工程应用上不区分这两个极限,统称为弹性极限。
② 在屈服阶段bc 内,应力几乎不增加,应变急剧增大,分别有上屈服极限和下屈服极限,通常取下屈服极限为材料的屈服强度或屈服极限σs 。
③ 在强化阶段cd 内,应力应变持续增加,曲线继续上升,材料恢复抵抗能力,d 点为名义应力的最大值,称为材料的强度极限或拉伸强度σb 。
④ 在局部变形阶段de 内,试样局部急剧缩小(颈缩),曲线下降。
冷作硬化:先将试样拉到强化阶段,卸载,当再加载时,试样的弹性极限将提高,但塑性变形降低。
冷作时效:先将试样拉到强化阶段,卸载,过一段时间再加载,弹性极限还会提高,但塑性也会降低。
2.1.2低碳钢与铸铁的压缩曲线(看一下即可)Eg强度高的曲线: 刚度高的曲线: 塑性好的曲线:σ1232.2轴力2.2.1轴力的计算与轴力图画法截面法:截开、确定方向、求解轴力。
方向的确定:取背离截面为n 方向,若保留部分与n 同向,则轴力为负;反之为正。
若保留1截面左边部分,则F N1=10kN,若保留1截面右边部分,则F N1=10kN 。
轴力图10F N 图(kN )2.2.2应力轴力是杆横截面上分布内力系的合力,而内力大小并不能衡量构件强度大小。
因此,必须知道分布内力大小的分布内力集度,即应力。
横截面上应力均匀分布σ=F N /A小结:① 讨论应力应明确是在哪一个截面上的哪一点处, ② 应力是矢量,规定离开截面的正应力为正(拉应力),反之为负, ③ 应力单位是Pa,1Pa=1N/m 2,1MPa=106Pa,1Gpa=109Pa ,④ 截面上应力σ与微面积dA 合成,即为该截面的内力,故横截面上正应力σ=F N /A →基于平面假设。
需了解:圣维南原理:当离力的作用点较远时,应力分布与大小不受外荷载作用方式(集中力、分布力、动荷载。
)的影响。
危险截面——最大轴力所在截面,最大工作应力——危险截面上的正应力。
斜截面上的应力状态(A 为横截面面积,A.。
=Acos α)1) 若α=0,σ= F N /A 最大,τ=02)若α=45°,τ=F N /2A 最大,σ= F N /2A 3)若α=90°,σ=0,τ=0+F=10KNF12.2.3应变——每单位长度的伸长或缩短ε=ll ∆=l l l -1(伸长为正,缩短为负)胡克定律:l ∆=lF N (只有当杆应力不超过材料的比例极限才成立)l l ∆=EA F N ε=Eσ(单轴应力状态下的胡克定律) F N ——轴力,l ——杆长,E ——弹性模量,EA ——杆的抗拉刚度,或拉伸(压缩)刚度例子:求杆件在重力作用下的伸长量。
已知杆的重度为γ,长为L ,横截面为A 。
2.3强度计算不出现强度破坏 保证构件不失效,在外力作用下能正常工作 不出现刚度破坏 不出现失稳破坏许用应力 σs ——塑性材料的屈服极限 极限应力 σb ——脆性材料的强度极限 =σmax≤[]σ=nu σ安全因数(强度储备)=极限应力/许用应力应用以上公式可出题的方式:强度校核、截面设计、许可荷载计算。
2.4拉压超静定未知力数超过独立平衡方程数的数目,称为超静定次数。
解法:先将某一处约束解除,加上一个相应的约束力,得到原超静定结构的基本静定系,然后综合运用a 静力学关系 b 变形几何关系 c 物理关系三方面条件求解。
温度与装配应力 Eg13剪切剪切面、挤压面的判断(单剪与双剪) 例子:τ=bd P bs σ=abP Eg24弯曲 剪切面 挤压面4.1一些概念弯曲——等直杆在承受垂直于杆轴线的横向外力或外力偶的作用下,杆轴线变形成为曲线,称为弯曲。
以弯曲为主要变形的杆件,统称为梁。
对称弯曲——梁变形后的轴线必定是一条在该纵对称面内的平面曲线,因此也称为平面弯曲。
纯弯曲——梁在对称弯曲时,若各横截面上的剪力为0,弯矩为常量,则该梁的弯曲弯曲称为纯弯曲。
△ 梁的计算简图 1.2. 3.4.2弯曲构件内力(梁、平面刚架)剪力F S :等于被保留端所有横向力的代数和 弯矩M :等于被保留端所有内力偶矩的代数和 方向规定:F S :绕研究对象顺时针转向为正剪力,反之为负M :该段下半部受拉时,横截面上的弯矩为正,反之为负 计算中采用的规定:F S :对所求截面的形心,顺时针的横向力引起正剪力M :不论在截面左侧还是右侧,向上的外力均引起正弯矩,向下引起负弯矩;对截面左侧的外力偶,则顺时针转向引起正值弯矩,逆时针引起负值弯矩,右侧相反绘图时:F S :正值剪力画在X 轴上侧,标明符号M :正值弯矩画在X 轴下侧,即受拉侧,标明符号 Eg :求1、2、3截面的剪力与1截面弯矩。
方法:1.去掉约束,加上约束反力,列方程求解 2.不求剪力与弯矩方程,简易方法作图 步骤:F S 图简易做法:从左到右,顺着荷载的起伏画图,从零点开始,最后回到零点 M 图简易做法:求出特殊点分段点的弯矩,描点,再连成相应的直线或曲线 需注意的是一些特殊点:荷载分段点、剪力等于0的点、集中力偶的两边 3.按叠加原理作弯矩图4.2.1纯弯曲纯弯曲时的正应力:横截面上任一点处的正应力与该点到中性轴的距离成正比,而在距中性轴为y 的等高线上各点处的正应力均相等。
等直梁在纯弯曲时横截面上任一点处弯曲正应力的计算公式:σ=E ε=Eρy=Ez EI My =zI MyMZ I 横截面对中性轴Z 的惯性矩,单位为m 4Z I = 对圆截面 Z I =644d π对矩形截面Z I =123bh当中性轴Z 为截面的对称轴时,横截面上的最大正应力,强度计算m ax σ==ZW M≤[]σ Z W 称为弯曲截面系数(m 3),可用来设计合理的截面形状(变截面梁、等强度梁等)Z W =m ax y I Z 对矩形截面 Z W =2h I Z =62bh对圆形截面 Z W =2d I Z =323d π对环形截面 Z W ==,α=DdEg44.2.2横力弯曲计算时仍可用纯弯曲的公式,只是m ax σ=中M(x)要换成相应截面上的弯矩梁的正应力强度条件:等直梁的最大正应力发生在最大弯矩的横截面上距中性轴最远的各点处4.3.弯曲变形梁的挠曲线近似微分方程``w =-,积分两次得,EIw=-⎰⎰dxdx x M )(+C 1x +C 2C 1、C 2可由边界条件确定:简支梁:左右两铰支座处挠度A ω、B ω均为0 悬臂梁:固定端处的挠度A ω和转角A θ也为0 铰接处:铰两端的挠度相等21ωω= 挠度计算: 1. 积分法分段写出弯矩方程,然后积分,并代入边界条件求解即可。
为使积分方便,常使后一个弯矩方程包含前一个弯矩方程。
例如,对(x-a)项积分时,就以(x-a)为自变量,由x=a处的边界条件ω左=ω右简化计算。
2.叠加法一般考的可能性较小,但要注意刚化原理。
Eg:等截面平面刚梁,求自由端A的水平位移和垂直位移。
a,给出AB段抗弯刚度EI。
b,给出AB段抗弯刚度EI和BC段抗拉刚度EA..重点:1)内力图:1.列方程画图 2.叠加原理 3.微分关系 4.简易法2)校核1.画剪力图、弯矩图2.形状规律3.突变规律4.分段规律5.微分关系dxdFs=q,=F(x)Eg45扭转(薄壁圆筒、等直圆杆)5.1薄壁圆筒的扭转横截面上无正应力,只产生垂直于半径方向的均匀分布的剪应力τ横截面上任一点处的切应力τ值均相等, τ=,A=π2r,r为平均半径,δ为壁厚q Fs M0 0 平0 平斜平斜抛薄壁圆筒表面上的切应变γ和相距为l 的两端面间的相互扭转角ϕ之间的关系:γ=ϕr/l 剪切胡克定律:τ=G γ,其中G 为材料的剪切(切变)模量剪应力互等(双生)定理:在单元体相互垂直的两个截面上,剪应力必然成对出现,且数值相等,两者都垂直于两个面的交线,其方向则共同指向或共同背离该交线。
5.2等直圆杆的扭转5.2.1扭矩与扭矩图方向规定:当力偶矢的指向离开截面时扭矩为正,反之为负 扭矩图:5.2.2扭转剪应力纯剪切时圆杆内平面上只有剪应力而无正应力,是纯剪切应力状态,ρτ=pI T ρ p I 为横截面的极惯性矩,是纯几何量,无物理意义,只与构件的大小形状有关,与材料无关,单位为m 4。
p I = 对实心圆截面,p I =324d π对空心圆截面,p I ==,α=Dd强度计算:m ax τ=p I TR =pW T ≤[]τ,其中p W 为抗扭截面系数(m 3) p W =RI p 对实心圆截面,p W =163d π对空心圆截面,p W ==,α=Dd 5.2.3扭转变形等直圆杆的扭转变形,用相对扭转角ϕ来衡量,ϕ=pGI Tl(rad ),G p I 称为等直圆杆的抗扭刚度刚度计算:单位长度扭转角'm ax ϕ=pGI T max≤[]'ϕ,其中[]'ϕ的单位是(°)/m ,故实际中的刚度校核用pGI T max ×π180≤[]'ϕEg36应力强度理论6.1平面应力状态截面的外法线与x 轴夹角α称为方位角,该截面为α截面规定:从x 轴到外法线n 逆时针转向的方位角为正值,而x τ则以沿单元体顺时针为正,y τ=-x τ6.1.1解析法求主平面:α截面的应力: ασ=+-x τα2sinατ=+x τα2cos一点处切应力等于0的截面称为主平面,主平面上的正应力称为主应力。
一点处必存在三个相互垂直的主应力,分别记为σ1、σ2、σ3,按代数值大小排列,例20MPa,0,-30MPa 由上面的式子可以看出,'ασ=-ατ,即正应力最大的平面剪应力为0,极值正应力一定是主应力;'ατ=0时,极值切应力与主平面成45°,可见切应力取极值时主应力并不为0。