2017中考数学考点总复习 第25节 圆的有关计算与尺规作图试题 新人教版

圆的有关计算与尺规作图1．如图，在△ABC 中，分别以点A 和点B 为圆心，大于12AB 的长为半径画弧，两弧相交于点M ，N ，作直线MN ，交BC 于点D ，连接AD .若△ADC 的周长为10，AB ＝7，则△ABC 的周长为( C )A ．7B ．14C ．17D ．202．(2016·无锡)已知圆锥的底面半径为4 cm ，母线长为6 cm ，则它的侧面展开图的面积等于( C )A ．24 cm 2B ．48 cm 2C ．24π cm 2D ．12π cm 23．(2016·成都)如图，AB 为⊙O 的直径，点C 在⊙O 上，若∠OCA ＝50°，AB ＝4，则BC ︵的长为( B )A.103πB.109πC.59πD.518π,第3题图) ,第4题图)4．(2016·资阳)在Rt △ABC 中，∠ACB ＝90°，AC ＝23，以点B 为圆心，BC 的长为半径作弧，交AB 于点D ，若点D 为AB 的中点，则阴影部分的面积是( A )A ．23－23πB ．43－23πC ．23－43π D.23π5．(2016·十堰)如图，从一张腰长为60 cm ，顶角为120°的等腰三角形铁皮OAB 中剪出一个最大的扇形OCD ，用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗)，则该圆锥的高为( D )A ．10 cmB ．15 cmC ．10 3 cmD ．20 2 cm,第5题图) ,第6题图)6．(2016·广安)如图，AB 是圆O 的直径，弦CD ⊥AB ，∠BCD ＝30°，CD ＝43，则S 阴影＝( B )A ．2π B.83π C.43π D.38π7．(2016·福州)如图所示的两段弧中，位于上方的弧半径为r 上，下方的弧半径为r 下，则r 上__＜__r 下．(填“＜”“＝”“＜”),第7题图) ,第9题图)8．(2016·眉山)一个圆锥的侧面展开图是半径为8 cm ，圆心角为120°的扇形，则此圆锥底面圆的半径为__83_cm__．9．(2016·邵阳)如图，在3×3的方格纸中，每个小方格都是边长为1的正方形，点O ，A ，B 均为格点，则扇形OAB 的面积大小是__5π4__．10．(导学号 59042188)(2016·东营)如图，某数学兴趣小组将边长为5的正方形铁丝框ABCD 变形为以A 为圆心，AB 为半径的扇形(忽略铁丝的粗细)，则所得的扇形ABD 的面积为__25__．11．(导学号 59042189)(2016·河南)如图，在扇形AOB 中，∠AOB ＝90°，以点A 为圆心，OA 的长为半径作OC ︵交AB ︵于点C ，若OA ＝2，则阴影部分的面积为__3－13π__．12．(2016·巴中)如图，在平面直角坐标系xOy 中，以点O 为圆心的圆分别交x 轴的正半轴于点M ，交y 轴的正半轴于点N .劣弧MN ︵的长为65π，直线y ＝－43x ＋4与x 轴、y 轴分别交于点A ，B .(1)求证：直线AB 与⊙O 相切；(2)求图中所示的阴影部分的面积．(结果用π表示)解：(1)作OD ⊥AB 于D ，∵劣弧MN ︵的长为65π，∴90π×OM 180＝65π，解得OM ＝125，即⊙O 的半径为125，∵直线y ＝－43x ＋4与x 轴、y 轴分别交于点A ，B ，当y ＝0时，x ＝3；当x ＝0时，y ＝4， ∴A (3，0)，B (0，4)，∴OA ＝3，OB ＝4，∴AB ＝32＋42＝5，∵△AOB 的面积＝12AB ·OD ＝12OA ·OB ，∴OD ＝OA ×OB AB ＝125＝半径OM ，∴直线AB 与⊙O 相切(2)图中所示的阴影部分的面积＝△AOB 的面积－扇形OMN 的面积＝12×3×4－14π×(125)2＝6－3625π13．(2015·玉林)如图，在⊙O 中，AB 是直径，点D 是⊙O 上一点且∠B OD ＝60°，过点D 作⊙O 的切线CD 交AB 的延长线于点C ，E 为AD ︵的中点．连接DE ，EB.(1)求证：四边形BCDE 是平行四边形；(2)已知图中阴影部分面积为6π，求⊙O 的半径r.解：(1)∵CD 是⊙O 的切线，∠BOD ＝60°，∴OD ⊥CD ，∠C ＝30°，∴∠DEB ＝12∠DOB＝30°，连接OE ，则∠AOE＝60°，∴∠EBA ＝12∠AOE＝30°，∴EB ∥CD ，ED ∥BC ，∴四边形BCDE 是平行四边形 (2)由(1)知OD⊥EB，设OD 与EB 交点为H ，∴BH ＝HE ，∴△OBH ≌△DEH ，∴阴影部分面积与扇形OBD 面积相等，∴S 阴影＝60πr2360＝6π，解得r ＝614．(导学号 59042190)如图，将边长为1 cm 的等边三角形ABC 沿直线l 向右翻动(不滑动)，点B 从开始到结束，所经过路径的长度为( C )A.32π cm B ．(2＋23π) cm C.43π cm D ．3 cm,第14题图),第15题图)15．(导学号 59042191)(2015·黑龙江)如图，从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC (A ，B ，C 三点在⊙O 上)，将剪下来的扇形围成一个圆锥的侧面，则该圆锥的底面圆的半径是4米．16．(导学号 59042192)(2016·宜昌)如图，CD 是⊙O 的弦，AB 是直径，且CD ∥AB ，连接AC ，AD ，OD ，其中AC ＝CD ，过点B 的切线交CD 的延长线于E .(1)求证：DA 平分∠CDO ； (2)若AB ＝12，求图中阴影部分的周长之和．(参考数据：π≈3.1，2≈1.4，3≈1.7)解：(1)∵CD ∥AB ， ∴∠CDA ＝∠BAD ， 又∵OA ＝OD ， ∴∠ADO ＝∠BAD ， ∴∠ADO ＝∠CDA ， ∴DA 平分∠CDO(2)连接BD ，∵AB 是直径，∴∠ADB ＝90°， ∵AC ＝CD ，∴∠CAD ＝∠CDA ， 又∵CD ∥AB ，∴∠CDA ＝∠BAD ，∴∠CDA ＝∠BAD ＝∠CAD ，∴AC ︵＝DC ︵＝DB ︵， 又∵∠AOB ＝180°，∴∠DOB ＝60°， ∵OD ＝OB ，∴△DOB 是等边三角形，∴BD ＝OB ＝12AB ＝6，∵AC ︵＝BD ︵，∴AC ＝BD ＝6， ∵BE 切⊙O 于B ，∴BE ⊥AB ， ∴∠DBE ＝∠ABE －∠ABD ＝30°， ∵CD ∥AB ，∴BE ⊥CE ，∴DE ＝12BD ＝3，BE ＝BD ·cos30°＝6×32＝33，∴BD ︵的长＝60π×6180＝2π，∴图中阴影部分周长之和为2π＋6＋2π＋3＋33＝4π＋9＋33≈4×3.1＋9＋3×1.7＝26.5。

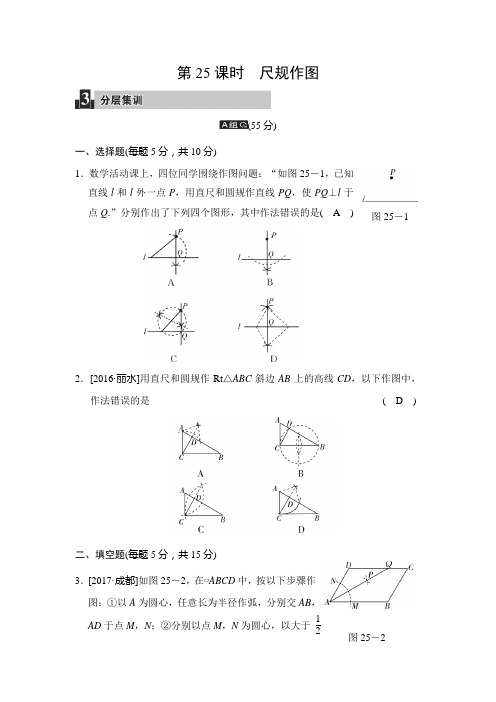
第25课时尺规作图(55分)一、选择题(每题5分，共10分)1．数学活动课上，四位同学围绕作图问题：“如图25－1，已知直线l和l外一点P，用直尺和圆规作直线PQ，使PQ⊥l于点Q.”分别作出了下列四个图形，其中作法错误的是(A)2．[2016·丽水]用直尺和圆规作Rt△ABC斜边AB上的高线CD，以下作图中，作法错误的是(D)二、填空题(每题5分，共15分)3．[2017·成都]如图25－2，在▱ABCD中，按以下步骤作图：①以A为圆心，任意长为半径作弧，分别交AB，AD于点M，N；②分别以点M，N为圆心，以大于12图25－1图25－2MN 的长为半径作弧，两弧相交于点P ；③作射线AP 交边CD 于点Q .若DQ ＝2QC ，BC ＝3，则▱ABCD 的周长为__15__．【解析】 由作图知，AQ 是∠BAD 的平分线，∴∠BAQ ＝∠DAQ ，又∵▱ABCD 中，CD ∥AB ，∴∠DQA ＝∠BAQ ＝∠DAQ ，∴DA ＝QD .∵DQ ＝2QC ，BC ＝3，∴DQ ＝3，QC ＝32，∴▱ABCD 的周长为2(BC ＋CD )＝2×⎝ ⎛⎭⎪⎫3＋3＋32＝15. 4．[2017·济宁] 如图25－3，在平面直角坐标系中，以O 为圆心，适当长为半径画弧，交x 轴于点M ，交y轴于点N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧在第二象限交于点P .若点P 的坐标为(a ，b )，则a 与b 的数量关系为__a ＋b ＝0__．【解析】 根据题目中作图步骤可得射线OP 即为∠MON 的角平分线，表达式即为y ＝－x ，所以点P 的坐标(a ，b )，a 与b 满足a ＋b ＝0.5．[2017·河北]如图25－4，依据尺规作图的痕迹，计算∠α＝__56__°.图25－4 第5题答图【解析】 ∵四边形ABCD 是矩形，∴AD ∥BC ，∴∠DAC ＝∠ACB ＝68°.∵由作法可知，AF 是∠DAC 的平分线，∴∠EAF ＝12∠DAC ＝34°.∵由作法可知，EF 是线段AC 的垂直平分线，图25－3∴∠AEF＝90°，∴∠AFE＝90°－34°＝56°，∴∠α＝56°.三、解答题(共30分)6．(15分) [2016·广州] 如图25－5，利用尺规，在△ABC的边AC上方作∠CAE ＝∠ACB，在射线AE上截取AD＝BC，连结CD，并证明：AB∥CD(尺规作图，要求保留作图痕迹，不写作法)．图25－5 第6题答图解：所求作的图形如答图所示．证明：∵∠CAE＝∠ACB，∴AD∥CB，∵AD＝BC，∴四边形ABCD是平行四边形，∴AB∥CD.7．(15分)[2016·孝感]如图25－6，在Rt△ABC中，∠ACB＝90°.(1)请用直尺和圆规按下列步骤作图，保留作图痕迹：①作∠ACB的平分线，交斜边AB于点D，②过点D作AC的垂线，垂足为E；(2)在(1)作出的图形中，若CB＝4，CA＝6，则DE＝__2.4__．图25－6第7题答图【解析】 (1)以C 为圆心，任意长为半径画弧(半径小于直角边)，交BC ，AC 于两点，再以这两点为圆心，大于这两点间线段的一半为半径画弧，过这两弧的交点与点C 的直线交AB 于点D 即可，根据过直线外一点作已知直线的垂线的方法可作出垂线；(2)根据平行线的性质和角平分线的性质推出∠ECD ＝∠EDC ，进而证得DE ＝CE ，由DE ∥BC ，推出△ADE ∽△ABC ，根据相似三角形的性质即可推得结论．解：(1)如答图所示；(2)∵CD 是∠ACB 的平分线，∴∠BCD ＝∠ECD ，∵DE ⊥AC ，BC ⊥AC ，∴DE ∥BC ，∴∠EDC ＝∠BCD ，∴∠ECD ＝∠EDC ，∴DE ＝CE ，∵DE ∥BC ，∴△ADE ∽△ABC ，∴DE BC ＝AE AC ，设DE ＝CE ＝x ，则AE ＝6－x ，∴x 4＝6－x 6，解得x ＝2.4，即DE ＝2.4.(30分)8．(15分)[2016·青岛]如图25－7，已知线段a 及∠ACB .求作：⊙O ，使⊙O 在∠ACB 的内部，CO ＝a ，且⊙O 与∠ACB 的两边分别相切．图25－7解：如答图所示，第8题答图①作∠ACB 的平分线CD ；②在CD 上截取CO ＝a ；③作OE ⊥CA 于点E ，以O 为圆心，OE 长为半径作圆，⊙O 即为所求．9．(15分)[2018·中考预测]如图25－8，已知△ABC ，按如下步骤作图： ①以A 为圆心，AB 长为半径画弧；②以C 为圆心，CB 长为半径画弧，两弧相交于点D ；③连结BD ，与AC 交于点E ，连结AD ，CD .(1)求证：△ABC ≌△ADC ；(2)若∠BAC ＝30°，∠BCA ＝45°，AC ＝4，求BE 的长．图25－8【解析】 (1)利用SSS 定理证得结论；(2)设BE ＝x ，利用特殊角的三角函数易得AE 的长，由∠BCA ＝45°，易得EC ＝BE ＝x ，由AC ＝AE ＋EC 解得x ，即BE 的长．解：(1)证明：在△ABC 和△ADC 中，⎩⎪⎨⎪⎧AB ＝AD ，BC ＝DC ，AC ＝AC ，∴△ABC ≌△ADC (SSS )；(2)设BE＝x，由题可知BD⊥AC，∵∠BAC＝30°，∴∠ABE＝60°，∴AE＝tan60°·x＝3x，∵∠BCA＝45°，∴∠CBE＝45°，∴EC＝BE＝x，∵AE＋EC＝AC，∴3x＋x＝4，解得x＝23－2，∴BE＝23－2.(15分)10．(15分)[2017·无锡]如图25－9，已知等边三角形ABC，请用直尺(不带刻度)和圆规，按下列要求作图(不要求写作法，但要保留作图痕迹)：(1)作△ABC的外心O；(2)设D是AB边上一点，在图中作出一个正六边形DEFGHI，使点F，点H分别在边BC和AC上．图25－9 备用图【解析】(1)三角形各边中垂线的交点即△ABC的外心O；(2)由(1)知点O到顶点A的距离是它到对边中点的两倍，作OA的中垂线交AB于点D，以O为圆心，OD为半径作圆交AB，BC，CA于E，F，G，H，I，连结EF，GH，正六边形DEFGHI即为所求．解：(1)如答图①，点O为△ABC的外心．第10题答图① 第10题答图②(2)如答图②，正六边形DEFGHI 即为所求．。

第25节 圆的有关计算与尺规作图一、选择题1．(2015·舟山)数学活动课上，四位同学围绕作图问题：“如图，已知直线l 和l 外一点P ，用直尺和圆规作直线PQ ，使PQ⊥l 于点Q”，分别作出了下列四个图形．其中作法错误的是( A )2．如图，正六边形螺帽的边长是2 cm ，这个扳手的开口a 的值应是( A ) A ．2 3 cm B. 3 cm C.233cm D ．1 cm,第2题图) ,第4题图)3．(2016·无锡)已知圆锥的底面半径为4 cm ，母线长为6 cm ，则它的侧面展开图的面积等于( C )A ．24 cm 2B ．48 cm 2C ．24π cm 2D ．12π cm 24．(2017·资阳预测)如图，在△ABC 中，分别以点A 和点B 为圆心，大于12AB 的长为半径画弧，两弧相交于点M ，N ，作直线MN ，交BC 于点D ，连接AD.若△ADC 的周长为10，AB ＝7，则△ABC 的周长为( C )A ．7B ．14C ．17D ．205．(2016·十堰)如图，从一张腰长为60 cm ，顶角为120°的等腰三角形铁皮OAB 中剪出一个最大的扇形OCD ，用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗)，则该圆锥的高为( D )A ．10 cmB ．15 cmC ．10 3 cmD ．20 2 cm6．(导学号 14952407)(2017·南充预测)如图，将边长为1 cm 的等边三角形ABC 沿直线l 向右翻动(不滑动)，点B 从开始到结束，所经过路径的长度为( C )A.32π cm B ．(2＋23π) cm C.43π cm D ．3 cm7．(导学号 14952408)(2016·枣庄)如图，AB 是⊙O 的直径，弦CD⊥AB，∠CDB ＝30°，CD ＝23，则阴影部分的面积为( D ) A ．2π B ．πC.π3 D.2π3二、填空题8．(2016·衡阳)若圆锥底面圆的周长为8π，侧面展开图的圆心角为90°，则该圆锥的母线长为__16__．9．(2016·安徽)如图，已知⊙O 的半径为2，A 为⊙O 外一点，过点A 作⊙O 的一条切线AB ，切点是B ，AO 的延长线交⊙O 于点C ，若∠BAC＝30°，则劣弧BC ︵的长为__4π3__．,第9题图) ,第10题图)10．(2016·威海)如图，正方形ABCD 内接于⊙O，其边长为4，则⊙O 的内接正三角形EFG 的边长为．11．几何体由圆锥和圆柱组成，其尺寸如图所示，则该几何体的全面积(即表面积)为__68π__．(结果保留π),第11题图),第12题图)12．(2016·鄂州)如图，扇形OAB 中，∠AOB ＝60°，OA ＝6 cm ，则图中阴影部分的面积是_cm 2__．13．(导学号 14952409)(2015·黑龙江)如图，从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A ，B ，C 三点在⊙O 上)，将剪下来的扇形围成一个圆锥的侧面，则该圆锥的底面圆的半径是4米． 三、解答题14．(2016·贵港)如图，在▱ABCD 中，AC 为对角线，AC ＝BC ＝5，AB ＝6，AE 是△ABC 的中线．(1)用无刻度的直尺画出△ABC 的高CH ；(保留画图痕迹) (2)求△ACE 的面积．解：(1)连接BD 交AE 于点F ，连接CF 并延长交AB 于点H (2)∵AC ＝BC ＝5，AB ＝6，CH ⊥AB ， ∴AH ＝12AB ＝3，∴CH ＝AC 2－AH 2＝4，∴S △ABC ＝12AB·CH ＝12×6×4＝12，∵AE 是△ABC 的中线， ∴S △ACE ＝12S △ABC ＝615．(2015·孝感)如图，一条公路的转弯处是一段圆弧(AB ︵)．(1)用直尺和圆规作出AB ︵所在圆的圆心O ；(要求保留作图痕迹，不写作法) (2)若AB ︵的中点C 到弦AB 的距离为20 m ，AB ＝80 m ，求AB ︵所在圆的半径．解：(1)作图略 (2)连接AB ，OB ，OC ，OC 交AB 于D ，∵AB ＝80，C 为AB ︵的中点，∴OC ⊥AB ，∴AD ＝BD ＝40，CD ＝20，设OB ＝r ，则OD ＝r －20，在Rt △OBD 中，OB 2＝OD 2＋BD 2，∴r 2＝(r －20)2＋402，解得r ＝50，∴AB ︵所在圆的半径是50 m16．(导学号 14952410)(2017·内江预测)如图，在⊙O 中，AB 是直径，点D 是⊙O 上一点且∠BOD ＝60°，过点D 作⊙O 的切线CD 交AB 的延长线于点C ，E 为AD ︵的中点．连接DE ，EB.(1)求证：四边形BCDE 是平行四边形；(2)已知图中阴影部分面积为6π，求⊙O 的半径r.解：(1)∵CD 是⊙O 的切线，∠BOD ＝60°，∴OD ⊥CD ，∠C ＝30°，∴∠DEB ＝12∠DOB＝30°，连接OE ，则∠AOE ＝60°，∴∠EBA ＝12∠AOE ＝30°，∴EB ∥CD ，ED ∥BC ，∴四边形BCDE 是平行四边形 (2)由(1)知OD⊥EB ，设OD 与EB 交点为H ，∴BH ＝HE ，∴△OB H≌△DHE ，∴阴影部分面积与扇形OBD 面积相等，∴S 阴影＝60πr2360＝6π，解得r ＝6。

与圆有关的计算【命题趋势】在中考中.圆有关的计算常以弧长.扇形面积.阴影部分面积.圆锥有关计算为主.占分值6分左右。

【中考考查重点】一、弧长、扇形面积的有关计算二、圆锥的有关计算三、阴影部分面积的计算考点：弧长.扇形与圆锥的有关计算设的半径为R.圆心角所对弧长为l.弧长公式：l=nπR180（弧长的长度和圆心角大小和半径的取值有关）扇形面积公式：圆锥的侧面积公式：122S l r rlππ==(其中l是圆锥的母线长.r是圆锥的底面半径)母线的概念：连接圆锥顶点和底面圆周任意一点的线段。

圆锥体表面积公式：（l为母线）【备注】1）圆锥的表面积=扇形面积=底面圆面积2）扇形的弧长为圆锥的底面圆周长2πR1.（2020秋•涟源市期末）若圆弧的半径为3.所对的圆心角为60°.则弧长为（）A．πB．πC．πD．3π【答案】B【解答】解：弧长l＝＝π.故选：B2.（2020•兰州）如图.现有一圆心角为90°.半径为8cm的扇形纸片.用它恰好围成一个圆锥的侧面（接缝忽略不计）.则该圆锥底面圆的半径为（）A．4cm B．3cm C．2cm D．1cm【答案】C【解答】解：弧长：＝4π（cm）.圆锥底面圆的半径：r＝＝2（cm）．故选：C．3.（2021•山西）如图.有一圆心角为120°.半径长为6cm的扇形.若将OA、OB重合后围成一圆锥侧面.那么圆锥的高是（）A．4cm B．cm C．2cm D．2cm【答案】A【解答】解：由圆心角为120°、半径长为6cm.可知扇形的弧长为＝4πcm.即圆锥的底面圆周长为4πcm.则底面圆半径为2cm.已知OA＝6cm.由勾股定理得圆锥的高是4cm．故选：A．4.（2020•枣庄）在Rt△ABC中.∠C＝90°.BC＝4cm.AC＝3cm．把△ABC绕点A顺时针旋转90°后.得到△AB1C1.如图所示.则点B所走过的路径长为（）A．5cm B．πcm C．πcm D．5πcm【答案】C【解答】解：在Rt△ABC中.AB＝＝＝5.l AB＝＝＝πcm.故点B所经过的路程为πcm．故选：C考点：阴影部分面积的计算求阴影部分面积的几种常见方法：1）公式法；2）割补法；3）拼凑法；4）等积变形构造方程法；5）去重法。

2017年全国中考数学真题分类与圆的有关计算填空题二、填空题1.（2017安徽中考13．·5分）如图，已知等边△ABC 的边长为6，以AB 为直径的⊙O 与边AC ，BC 分别交于D ，E 两点，则劣弧DE 错误!未定义书签。

的长为答案：π．解析：连接OD ，OE ，易证△ODE 是等边三角形，∠DOE ＝60°，又OD ＝12AB ＝3，根据弧长公式劣弧DE 错误!未定义书签。

的长为603180ππ⋅⋅=．2. （2017山东济宁，15，3分）如图，正六边形111111A B C D E F 的边长为1，它的6条对角线又围成一个正六边形222222A B C D E F ，如此继续下去，则六边形444444A B C D E F 的面积是．3，解析：根据“正多边形各边都相等，各角都相等”由此可得△A 1A 2B 1与△A 1F 1F 2是等腰三角形，△A 1A 2F 2是等边三角形，所以A 2B 1＝ A 2F 2＝ F 1F 2，由此计算可得正六边形222222A B C D E F 的边长为3，正六边形111111A B C D E F 的边长为1，即正六边形222222A B C D E F 与正六边形111111A B C D E F 的相似比等于3，故面积之比为231=3⎛⎫ ⎪ ⎪⎝⎭，由正六边形111111A B C D E F 的面积为13336112S =⨯⨯⨯⨯=，所以六边形444444A B C D E F 的面积是333133S ⎛⎫=⨯= ⎪⎝⎭． 3. （2017山东菏泽，12,3分）一个扇形的圆心角为100°，面积为15π2cm ，则此扇形的半径长为 ．答案:36,解析:因为圆心角为100°，面积为15π2cm ，所以由扇形面积公式2360n R S π=得3603601536100S R n πππ⨯===. 4. （2017四川自贡,16,3分）圆锥的底面周长为6πcm ，高为4cm ，则该圆锥的全面积是 ；侧面展开扇形的圆心角是 .答案：24π，216°，解析：圆锥的底面周长为6π，∴底面半径为r =6π÷2π=3，根据勾股定理，得圆锥的母线R =222234r h +=+=5，侧面展开扇形的弧长l ＝2πr ＝6π，∴侧面展开扇形的面积S 侧=1122lR =×6π×5=15π，底面积S 底=πr 2=9π，∴该圆锥的全面积S 全=15π+9π=24π；设侧面展开扇形的圆心角为n °，则=180n R l π，即5=6180n ππ⨯，解得n =216.5. （2017重庆B ，15，4分）如图，OA ，OC 是⊙O 的半径，点B 在⊙O 上连接AB ，BC ，若∠ABC =40°,则∠AOC = 度.答案：80，解析：∠ABC 和∠AOC 都是弧AC 所对的圆周角和圆心角，根据圆周角定理，“在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角度数的一半”， ∴圆周角∠ABC =40°，则圆心角∠AOC =40°×2=80°．6. （2017浙江舟山，13，4分）如图，小明自制一块乒乓球拍，正面是半径为8cm 的⊙O ，BCAABm＝ 90°，弓形ACB（阴影部分）粘贴胶皮，则胶皮面积为．答案：32（cm）2，解析：连接AO，OB，作OD⊥AB于D．因为90ABm=︒，所以∠AOB＝90°，所以S扇形ACB＝S⊙O－S△OAB＝34×π×82+12×8×8＝48π+32（cm）2.7.（2017江苏盐城，15，3分）如图，在边长为1的小正方形网格中，将△ABC绕某点旋转到△A′B′C′的位置，则点B运动的最短路径长为________．13，解析：①先确定旋转中心．作线段CC′的垂直平分线；连接AA′，作线段AA′的垂直平分线交于点O，点O恰好在格点上；②确定最小旋转角．最小旋转角为90°；③确定旋转半径．连接OB，由勾股定理得OB2223+13所以点B90π13⋅13．8.(2017年四川内江，15，4分)如图，AB是⊙O的直径，弦CD⊥AB于点E，⊙O半径为3cm，弦第15题图CABC'B'A'CABC'B'A'OCD 的长为3cm ，则阴影部分的面积是 .答案：(π－433)cm 2，解析：∵CD ⊥AB ，∴CE ＝21CD ＝23． 在Rt △OEC 中，sin ∠COE ＝323=OC CE＝23． ∴∠COE ＝60°． ∴OE =OC cos ∠COE ＝3×21＝23.∴S △OCD ＝21OE ·CD ＝21×23×3＝433.∵∠COE ＝60°，∴∠COD ＝120°．∴S 扇形OCD =360)3(1202⨯π＝π．∴阴影部分的面积是S 扇形OCD －S △OCD ＝(π－433)cm 2.9. （2017山东泰安，23，3分）工人师傅用一张半径24c m ，圆心角为150°的扇形铁皮做成一个圆锥的侧面，则这个圆锥的高为_______．答案：119c m ，解析：由题意可得圆锥的母线长为24c m ，设圆锥的底面圆的半径为rc m ，则150242180r ππ⨯=，解得r=10（c m ）2224102119-=m ．10. 16．（2017江苏无锡，16，2分）已知圆锥的底面半径为3cm ，母线长为5cm ，则它的侧面展开图的面积等于 cm 2． 答案：15π.解析：圆锥的底面半径为3cm ，则圆锥的底面周长为6πcm ．∵母线长为5cm ，∴它的侧面展开图的扇形面积 ＝12×6π×5 ＝15π（cm 2）．11. 17．（2017江苏无锡，17，2分）如图，已知矩形ABCD 中，AB ＝3，AD ＝2，分别以边AD 、BC为直径在矩形ABCD 的内部作半圆O 1和半圆O 2，一平行于AB 的直线EF 与这两个半圆分别交于点E 、点F ，且EF ＝2（EF 与AB 在圆O 1和O 2的同侧），则由ΑΕ、EF 、F Β、AB 所围成图形（图中阴影部分）的面积等于 ．O 2O A答案：72－6π· 解析：如图，连接AE ，延长FE 交AD 于G ，则EG ⊥AD ． ∵AB ＝3，EF ＝2，∴EG ＝0.5． ∵AD ＝2，∴O 1 A ＝O 1E ＝1． ∴∠AO 1E ＝30°． ∴O 1G∴AG ＝1∵弓形AmE 的面积＝扇形O 1AE 的面积－△O 1AE 的面积＝2301360π⋅⋅－12O 1A ·EG＝12π－12×1×0.5 ＝12π－14·∴图中阴影部分的面积＝梯形的面积－2×弓形AmE 的面积 ＝12( EF ＋AB )·AG －2×（12π－12）＝12( 2＋3)·(1－6π＋1＝72－6π·GO 2O A12. 13．（2017浙江温州，13，5分）已知扇形的面积为3π，圆心角为120°，则它的半径为_________．答案：3，解析：设扇形的半径为r ，由扇形的面积公式S ＝错误!未找到引用源。

2017年中考备考专题复习：尺规作图一、单选题1、下列属于尺规作图的是（）A、用刻度尺和圆规作△ABCB、用量角器画一个300的角C、用圆规画半径2cm的圆D、作一条线段等于已知线段2、下列画图语句中，正确的是（）A、画射线OP=3cmB、连接A ， B两点C、画出A ， B两点的中点D、画出A ， B两点的距离3、下列属于尺规作图的是（）A、用刻度尺和圆规作△ABCB、用量角器画一个30°的角C、用圆规画半径2cm的圆D、作一条线段等于已知线段4、下列关于几何画图的语句正确的是（）A、延长射线AB到点C ，使BC=2ABB、点P在线段AB上，点Q在直线AB的反向延长线上C、将射线OA绕点O旋转180°，终边OB与始边OA的夹角为一个平角D、已知线段a ， b满足2a＞b＞0，在同一直线上作线段AB=2a ， BC=b ，那么线段AC=2a-b5、尺规作图是指（）A、用量角器和刻度尺作图B、用圆规和有刻度的直尺作图C、用圆规和无刻度的直尺作图D、用量角器和无刻度的直尺作图6、下列有关作图的叙述中，正确的是（）A、延长直线ABB、延长射线OMC、延长线段AB到C ，使BC=ABD、画直线AB=3cm7、按下列条件画三角形，能唯一确定三角形形状和大小的是（）A、三角形的一个内角为60°，一条边长为3cmB、三角形的两个内角为30°和70°C、三角形的两条边长分别为3cm和5cmD、三角形的三条边长分别为4cm、5cm和8cm8、下列属于尺规作图的是（）A、用刻度尺和圆规作△ABCB、用量角器画一个300的角C、用圆规画半径2cm的圆D、作一条线段等于已知线段9、下列关于几何画图的语句正确的是（）A、延长射线AB到点C ，使BC=2ABB、点P在线段AB上，点Q在直线AB的反向延长线上C、将射线OA绕点O旋转180°，终边OB与始边OA的夹角为一个平角D、已知线段a ， b满足2a＞b＞0，在同一直线上作线段AB=2a ， BC=b ，那么线段AC=2a-b10、尺规作图是指（）A、用量角器和刻度尺作图B、用圆规和有刻度的直尺作图C、用圆规和无刻度的直尺作图D、用量角器和无刻度的直尺作图11、下列有关作图的叙述中，正确的是（）A、延长直线ABB、延长射线OMC、延长线段AB到C ，使BC=ABD、画直线AB=3cm12、下列作图语句中，不准确的是（）A、过点A、B作直线ABB、以O为圆心作弧C、在射线AM上截取AB=aD、延长线段AB到D ，使DB=AB二、填空题13、所谓尺规作图中的尺规是指：________．14、尺规作图“作一个角等于已知角“的依据是三角形全等的判定方法________15、用直尺和圆规作一个角等于已知角的示意图如图所示，则说明△DOC≌△D'O'C'的依据是________．16、如图，在△ABC中，∠C=90°，∠B=20°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N ，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于P ，连接AP并延长交BC于点D ，则∠ADB=________°．17、如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N ，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P ，连结AP并延长交BC于点D ，则下列说法①AD是∠BAC的平分线；②∠ADC=60°；③点D在AB的中垂线上；正确的个数是________个三、作图题18、已知：如图△ABC ．求作：①AC边上的高BD；②△ABC的角平分线CE ．19、如图所示，已知△ABC：①过A画出中线AD；②画出角平分线CE；③作AC边上的高BF20、（2016•兰州）如图，已知⊙O，用尺规作⊙O的内接正四边形ABCD．（写出结论，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔描黑）四、解答题21、已知直线l和l上一点P ，用尺规作l的垂线，使它经过点P ．你能明白小明的作法吗？你是怎样作的？22、如图，已知△ABC和直线m ，画出与△ABC关于直线m对称的图形（不要求写出画法，但应保留作图痕迹）答案解析部分一、单选题1、【答案】D【考点】作图—尺规作图的定义【解析】【解答】A.用刻度尺和圆规作△ABC ，而尺规作图中的直尺是没有长度的，错误；B.量角器不在尺规作图的工具里，错误；C.画半径2cm的圆，需要知道长度，而尺规作图中的直尺是没有长度的，错误；D.正确．选D．【分析】根据尺规作图的定义分别分析2、【答案】B【考点】作图—尺规作图的定义【解析】【解答】A.射线没有长度，错误；B.连接A ， B两点是作出线段AB ，正确；C.画出A ， B两点的线段，量出中点，错误；D.量出A ， B两点的距离，错误选B．【分析】根据基本作图的方法，逐项分析，从而得出正确的结论3、【答案】D【考点】作图—尺规作图的定义【解析】【解答】A.用刻度尺和圆规作△ABC ，而尺规作图中的直尺是没有长度的，错误；B.量角器不在尺规作图的工具里，错误；C.画半径2cm的圆，需要知道长度，而尺规作图中的直尺是没有长度的，错误；D.正确选：D．【分析】根据尺规作图的定义分别分析4、【答案】C【考点】作图—尺规作图的定义【解析】【解答】A.延长射线AB到点C ，使BC=2AB ，说法错误，不能延长射线；B.点P在线段AB 上，点Q在直线AB的反向延长线上，说法错误，直线本身是向两方无限延长的，不能说延长直线；C.将射线OA绕点O旋转180°，终边OB与始边OA的夹角为一个平角，说法正确；D.已知线段a ， b满足2a＞b＞0，在同一直线上作线段AB=2a ， BC=b ，那么线段AC=2a-b ，说法错误，AC也可能为2a+b选：C．【分析】根据射线、直线、以及角的定义可判断出正确答案5、【答案】C【考点】作图—尺规作图的定义【解析】【解答】尺规作图所用的作图工具是指不带刻度的直尺和圆规选：C ．【解析】【解答】A.直线本身是向两方无限延伸的，故不能延长直线AB ，故此选项错误；B.射线本身是向一方无限延伸的，不能延长射线OM ，可以反向延长，故此选项错误；C.延长线段AB到C ，使BC=AB ，说法正确，故此选项正确；D.直线本身是向两方无限延伸的，故此选项错误；选：C【分析】根据直线、射线和线段的特点分别进行分析7、【答案】D【考点】作图—尺规作图的定义【解析】【解答】A.三角形的一个内角为60°，一条边长为3cm ，既不能唯一确定三角形形状和也不能唯一确定大小，不符合题意；B.三角形的两个内角为30°和70°，能唯一确定三角形形状和但不能唯一确定大小，不符合题意；C.三角形的两条边长分别为3cm和5cm ，既不能唯一确定三角形形状和也不能唯一确定大小，不符合题意；D.三角形的三条边长分别为4cm、5cm和8cm ，能唯一确定三角形形状和大小，符合题意选：D．【分析】根据基本作图的方法，及唯一确定三角形形状和大小的条件可知8、【答案】D【考点】作图—尺规作图的定义【解析】【解答】A.用刻度尺和圆规作△ABC ，而尺规作图中的直尺是没有长度的，错误；B.量角器不在尺规作图的工具里，错误；C.画半径2cm的圆，需要知道长度，而尺规作图中的直尺是没有长度的，错误；D.正确选：D．【分析】根据尺规作图的定义分别分析9、【答案】C【考点】作图—尺规作图的定义【解析】【解答】A.延长射线AB到点C ，使BC=2AB ，说法错误，不能延长射线；B.点P在线段AB 上，点Q在直线AB的反向延长线上，说法错误，直线本身是向两方无限延长的，不能说延长直线；C.将射线OA绕点O旋转180°，终边OB与始边OA的夹角为一个平角，说法正确；D.已知线段a ， b满足2a＞b＞0，在同一直线上作线段AB=2a ， BC=b ，那么线段AC=2a-b ，说法错误，AC也可能为2a+b选：C．【分析】根据射线、直线、以及角的定义可判断出正确答案10、【答案】C【考点】作图—尺规作图的定义【解析】【解答】尺规作图所用的作图工具是指不带刻度的直尺和圆规选：C ．【解析】【解答】A.直线本身是向两方无限延伸的，故不能延长直线AB ，故此选项错误；B.射线本身是向一方无限延伸的，不能延长射线OM ，可以反向延长，故此选项错误；C.延长线段AB到C ，使BC=AB ，说法正确，故此选项正确；D.直线本身是向两方无限延伸的，故此选项错误；选：C【分析】根据直线、射线和线段的特点分别进行分析12、【答案】B【考点】作图—尺规作图的定义【解析】【解答】A.根据直线的性质公理：两点确定一条直线，可知该选项正确；B.画弧既需要圆心，还需要半径，缺少半径长，故该选项错误；C.射线有一个端点，可以其端点截取任意线段，故选项正确；D.线段有具体的长度，可延长，正确选：B．【分析】根据基本作图的方法，逐项分析，从而得出正确的结论二、填空题13、【答案】没有刻度的直尺和圆规【考点】作图—尺规作图的定义【解析】【解答】由尺规作图的概念可知：尺规作图中的尺规指的是没有刻度的直尺和圆规【分析】本题考的是尺规作图的基本概念14、【答案】SSS【考点】作图—尺规作图的定义【解析】【解答】在尺规作图中，作一个角等于已知角是通过构建三边对应相等的全等三角形来证，因此由作法知其判定依据是SSS ，即边边边公理【分析】通过对尺规作图过程的探究，找出三条对应相等的线段，判断三角形全等．因此判定三角形全等的依据是边边边公理15、【答案】SSS【考点】作图—尺规作图的定义【解析】【解答】OC=O′C′，OD=O′D′，CD=C′D′，从而可以利用SSS判定其全等【分析】①以O为圆心，任意长为半径用圆规画弧，分别交OA、OB于点C、D；②任意画一点O′，画射线O'A'，以O'为圆心，OC长为半径画弧C'E ，交O'A'于点C'；③以C'为圆心，CD长为半径画弧，交弧C'E于点D'；④过点D'画射线O'B'，∠A'O'B'就是与∠AOB相等的角．则通过作图我们可以得到OC=O′C′，OD=O′D′，CD=C′D′，从而可以利用SSS判定其全等16、【答案】125【考点】作图—基本作图【解析】【解答】由题意可得：AD平分∠CAB ，∵∠C=90°，∠B=20°，∴∠CAB=70°，∴∠CAD=∠BAD=35°，∴∠ADB=180°-20°-35°=125°【分析】根据角平分线的作法可得AD平分∠CAB ，再根据三角形内角和定理可得∠ADB的度数17、【答案】3【考点】作图—基本作图【解析】【解答】①AD是∠BAC的平分线，说法正确；②∵∠C=90°，∠B=30°，∴∠CAB=60°，∵AD平分∠CAB ，∴∠DAB=30°，∴∠ADC=30°+30°=60°，因此∠ADC=60°正确；③∵∠DAB=30°，∠B=30°，∴AD=BD【分析】根据角平分线的作法可得①正确，再根据三角形内角和定理和外角与内角的关系可得∠ADC=60°，再根据线段垂直平分线的性质逆定理可得③正确三、作图题18、【答案】解: 如图所示：【考点】作图—基本作图【解析】【分析】①以点B为圆心，较大的长为半径画弧，交直线AC于两点，分别以这两点为圆心，大于这两点的距离的一半为半径画弧，两弧相交于一点，过点B和这点作射线，交直线AC于点D ， BD就是所求的AC边上的高；②以点C为圆心，任意长为半径画弧，交CA ， CB于两点，分别以这两点为圆心，以大于这两点的距离的一半为半径画弧，两弧相交于一点，做过点C和这点的射线交AB于点E ， CE即为所求的角平分线19、【答案】解答：如图所示：【考点】作图—复杂作图【解析】【分析】（1）首先找出BC的中点，然后画线段AD即可；（2）利用量角器量出∠BCA的度数，再除以2，算出度数，然后画出线段CE即可；（3）利用直角三角板，一个直角边与AC重合，令一条直角边过点B ，画线段BF即可20、【答案】解：如图所示，四边形ABCD即为所求：【考点】正多边形和圆，作图—复杂作图【解析】【分析】画圆的一条直径AC，作这条直径的中垂线交⊙O于点BD，连结ABCD就是圆内接正四边形ABCD．本题考查的是复杂作图和正多边形和圆的知识，掌握中心角相等且都相等90°的四边形是正四边形以及线段垂直平分线的作法是解题的关键．四、解答题21、【答案】解：明白．作法：①以点P为圆心，以任意长为半径画圆，与直线l相交于点A ， B；②分别以AB为圆心，以任意长为半径画圆，两圆相交于点MN ，连接MN即可得出直线l的垂线【考点】作图—复杂作图【解析】【分析】根据线段垂直平分线的作法即可得出结论．22、【答案】【解答】如图所示，△A′B′C′即为△ABC关于直线m对称的图形．【考点】作图—尺规作图的定义，作图—基本作图，作图—复杂作图，轴对称图形【解析】【分析】找出点A、B、C关于直线m的对称点的位置，然后顺次连接即可．。

类型2：圆与三角函数、相似（1）求线段长、三角函数值 1、（黄冈中考20）已知：如图，MN 为⊙O 的直径，ME 是⊙O 的弦，MD 垂直于过点E 的直线DE ，垂足为点D ，且ME 平分∠DMN ． 求证：（1）DE 是⊙O 的切线；（2）ME 2=MD •MN ． 2、（顺义二模25）如图，在Rt △ABC 中，∠CAB =90︒，以AB 为直径的⊙O 交BC 于点D ，点E 是AC 的中点，连接DE ． （1）求证：DE 是⊙O 的切线；（2）点P 是»BD 上一点，连接AP ，DP ，若BD :CD=4:1，求sin ∠APD 的值．3、（苏州中考27）如图，已知△ABC 内接于⊙O ，AB 是直径，点D 在⊙O 上，OD ∥BC ，过点D 作DE ⊥AB ，垂足为E ，连接CD 交OE 边于点F ． （1）求证：△DOE ∽△ABC ；（2）求证：∠ODF =∠BDE ；（3）连接OC ，设△DOE 面积为1S ，四边形BCOD 面积为2S ，若1227S S =，求sin A 的值．A B C DE O4、（西城一模25）如图，AB为⊙O的直径，C为⊙O上一点，过点C作⊙O的切线，交BA的延长线交于点D，过点B作BE⊥BA，交DC延长线于点E，连接OE，交⊙O于点F，交BC于点H，连接AC．（1）求证：∠ECB =∠EBC；（2）连接BF，CF，若CF =6，sin∠FCB =35，求AC的长．5、（怀柔一模25）如图，在△ABC中，点D为BC上一点，过A，B，D三点作⊙O，AE是⊙O的直径，AC是⊙O的切线，AD=DC，连结DE．（1）求证：AB=AC;（2）若1sin3E ，AC=，求△ADE的周长（用含a的代数式表示）.D6、（门头沟一模25）如图，CD 为⊙O 的直径，点B 在⊙O 上，连接BC 、BD ，过点B 的切线AE 与CD 的延长线交于点A ，AEO C ∠=∠，OE 交BC 于点F . （1）求证：OE ∥BD ；（2）当⊙O 的半径为5，2sin 5DBA ∠=时，求EF 的长.7、（西城二模25）如图，AB 是⊙O 的直径，C 是⊙O 上一点，过点B 作⊙O 的切线，与AC延长线交于点D ，连接BC ，OE ∥BC 交⊙O 于点E ，连接BE 交AC 于点H ． （1）求证：BE 平分∠ABC ；（2）连接OD ，若BH =BD =2，求OD 的长．8、（丰台二模26）如图，AB 为半圆的直径，O 为圆心，C 为圆弧上一点，AD 垂直于过点C的切线，垂足为点D ，AB 的延长线交切线CD 于点E ． （1）求证：AC 平分∠DAB ；（2）若AB =4，B 为OE 的中点，CF ⊥AB ，垂足为点F ，求CF 的长.9、（昌平二模25）如图，AB 为⊙O 的直径，点D ，E 为⊙O 上的两个点，延长AD 至C ，使∠CBD=∠BED .（1）求证：BC 是⊙O 的切线；（2）当点E 为弧AD 的中点且∠BED=30°时，⊙O 半径为2，求DF 的长度.B CA10、（通州二模24）如图，AB是⊙O的直径，PC切⊙O于点C，AB的延长线与PC交于点P，PC的延长线与AD交于点D，AC平分∠DAB.（1）求证：AD⊥PC；（2）连接BC，如果∠ABC＝60°，BC＝2，求线段PC的长．11、（东城二模25）如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD交AD的延长线于点E．（1）求证：∠BDC=∠A；（2）若CE=4，DE=2，求AD的长．PBOACOE G D C B A 12、（怀柔二模25）如图，AB 是⊙O 的直径，CD 为⊙O 的弦，过点B 作⊙O 的切线交AD延长线于点E ，连接AC 并延长，过点E 作EG ⊥AC 延长线于点G ，并且∠GCD = ∠GAB .（1）求证：»»AC BD； （2）若AB =10，sin ∠ADC =35，求AG 的长．13、（平谷二模25）如图，已知△ABC 内接于⊙O ，AB 是⊙O 的直径，点F 在⊙O 上，且点C 是»BF的中点，过点C 作⊙O 的切线交AB 的延长线于点D ，交AF 的延长线于点E ． （1）求证：AE ⊥DE ； （2）若∠BAF =60°，AF =4，求CE 的长．14、（北京中考24）如图，AB 是O e 的一条弦，E 是AB 的中点，过点E 作EC OA ⊥于点C ，过点B 作O e 的切线交CE 的延长线于点D . （1）求证：DB DE =；（2）若12,5AB BD ==，求O e 的半径.15、（成都中考20） 如图，在ABC ∆中，AB AC =，以AB 为直径作圆O ，分别交BC 于点D ，交CA 的延长线于点E ，过点D 作DH AC ⊥于点H ，连接DE 交线段OA 于点F .（1）求证：DH 是圆O 的切线；（2）若A 为EH 的中点，求EFFD的值；（3）若1EA EF ==，求圆O 的半径.*16、（上海中考25）如图，已知⊙O的半径长为1，AB、AC是⊙O的两条弦，且AB=AC，BO的延长线交AC于点D，联结OA、OC．（1）求证：△OAD∽△ABD；（2）当△OCD是直角三角形时，求B、C两点的距离；（3）记△AOB、△AOD、△COD的面积分别为S1、S2、S3，如果S2是S1和S3的比例中项，求OD的长．*17、（杭州中考23）如图，已知△ABC内接于⊙O，点C在劣弧AB上（不与点A，B重合），点D为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=ɑ，∠ACB=β，∠EAG+∠EBA=γ，（1）点点同学通过画图和测量得到以下近似．．数据：ɑ30°40°50°60°β120°130°140°150°γ150°140°130°120°猜想：β关于（2）若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长。