数理统计第一次大作业
- 格式:pdf
- 大小:283.04 KB
- 文档页数:11

应用数理统计大作业1——逐步回归法分析终应用数理统计多元线性回归分析(第一次作业)学院:机械工程及自动化学院姓名:学号:2014年12月逐步回归法在AMHS物流仿真结果中的应用摘要:本文针对自动化物料搬运系统 (Automatic Material Handling System,AMHS)的仿真结果,根据逐步回归法,使用软件IBM SPSS Statistics 20,对仿真数据进行分析处理,得到多元线性回归方程,建立了工件年产量箱数与EMS 数量、周转箱交换周期以及AGC物料交换服务水平之间的数学模型,并对影响年产量箱数的显著性因素进行了分析,介绍了基本假设检验的情况。
关键词:逐步回归;残差;SPSS;AMHS;物流仿真目录1、引言 (1)2、逐步回归法原理 (4)3、模型建立 (6)3.1确定自变量和因变量 (6)3.2分析数据准备 (6)3.3逐步回归分析 (7)4、结果输出及分析 (9)4.1输入/移去的变量 (9)4.2模型汇总 (10)4.3方差分析 (10)4.4回归系数 (11)4.5已排除的变量 (12)4.6残差统计量 (13)4.7残差分布直方图和观测量累计概率P-P图 (14)5、异常情况说明 (15)5.1异方差检验 (15)5.2残差的独立性检验 (17)5.3多重共线性检验 (17)6、结论 (18)参考文献 (20)1、引言回归被用于研究可以测量的变量之间的关系,线性回归则被用于研究一类特殊的关系,即可用直线或多维的直线描述的关系。
这一技术被用于几乎所有的研究领域,包括社会科学、物理、生物、科技、经济和人文科学。
逐步回归是在剔除自变量间相互作用、相互影响的前提下,计算各个自变量x与因变量y之间的相关性,并在此基础上建立对因变量y有最大影响的变量子集的回归方程。
SPSS(Statistical Package for the Social Science社会科学统计软件包)是世界著名的统计软件之一,目前SPSS公司已将它的英文名称更改为Statistical Product and Service Solution,意为“统计产品与服务解决方案”。

数理统计第一次课程论文广州恒大队在2015赛季亚冠的进球数的多元线性回归模型学号: SY1527205姓名:郭谢有摘要本赛季亚洲冠军联赛,来自中国的球队广州恒大淘宝队最终在决赛中力克阿联酋的迪拜阿赫利队,三年之内第二次夺得亚冠冠军。
为了研究恒大的夺冠过程,本文选取了恒大该赛季亚冠总共15场比赛中的进球数为因变量,对可能影响进球数的射门数、射正数等7个自变量进行统计,并进一步利用统计软件SPSS对以上数据进行了多元逐步线性回归。
最终确定了进球数与各因素之间关系的“最优”回归方程。
关键词:多元线性回归,逐步回归法,广州恒大,SPSS目录摘要 (1)1.引言 (3)2.符号说明 (3)3.数据的采集和整理 (3)3.1数据的采集 (3)3.2建模 (4)4.数据分析及计算 (4)4.结论 (9)参考文献 (10)致谢 (10)1.引言一场足球比赛的进球数说明了一支球队攻击力的强弱,也是决定比赛胜负的至关因素,综合反映出这支球队的实际水平。
而作为竞技体育,足球场上影响进球数的因素很多,为了研究本赛季恒大在亚冠夺冠过程中的14场比赛中进球数与其他一些因素的关系,本论文从搜达足球和新浪体育数据库中查找了进球数和其他7个主要影响因素的数据,包括射门次数、射正次数、传球次数、传中次数、角球次数、抢断次数。
并进一步采用多元逐步回归分析方法对以上因素进行了显著性分析,从而确定了关于恒大在本赛季亚冠中进球数的最优多元线型回归方程。
2.符号说明3.数据的采集和整理3.1数据的采集本文统计数据时,查阅了搜达足球数据库,确定恒大在亚冠14场比赛中的进球数为因变量,并初步选取这14场比赛中的射门次数、射正次数、传球次数、传中次数、角球次数、抢断次数7因素为自变量,具体数据见下表1。
3.2建模本文选取了恒大在亚冠比赛中的进球数作为因变量y,并选取可能对进球数造成影响的因素为自变量,其中对应关系在符号说明中已经列举。
这里构建模型如下:7⋅X i+εy=β0+∑βii=1其中,其中ε为随机误差项,β0为常数项,βi为待估计的参数。

概率论与数理统计第1次作业
1、设随机事件A和B互不相容,且P(A)>0, P(B)>0, 则( )
(A) (B)
(C) (D )
2、袋中有5个白球和3个黑球,从中任取2个球,则取得的两球恰有一黑球的概率为 ______
3、袋中有8个球,其中6个新球,2个旧球,今从袋中随意取走3个球后,
再从剩下的球中任取一个,它恰为新球的概率为 .
4、任意将10本书放在书架上,其中有两套书,一套含三卷,另一套含四
卷,则两套各自放在一起的概率为 ______ .
5、设在全部产品中有2%是废品,而合格品有85%是一级品,求任抽出一
个产品它是一级品的概率 。
6、从0,1,2,…,9共10个数中任取一数,设每个数以的概率被取中,取后
放回,先后取出7个数,求下列事件的概率:
(1)A1={7个数全不相同};(2)A2={不含0和1};( 3)A3={0恰好出现2次};
7、已知事件A发生必导致 B发生,且,求.
8、已知,,,试求:(1);(2)
9、设A, B, C是随机事件,A, C互不相容,,求.
10、某人到武汉参加会议,他乘火车、轮船、汽车或飞机去的概率分别为0.2,0.1,0.3,0.4.如果他乘火车、轮船、汽车前去,迟到的概率分别为和,乘飞机去不会迟到.
试求:(1)他迟到的概率;
(2)如果他迟到了,求他是乘汽车去的概率.。

概率论与数理统计作业及解答第一次作业★1. 甲, 乙, 丙三门炮各向同一目标发射一枚炮弹, 设事件A , B , C 分别表示甲, 乙, 丙击中目标, 则三门炮最多有一门炮击中目标如何表示. 事件E ={事件,,A B C 最多有一个发生},则E 的表示为;E ABC ABC ABC ABC =+++或;ABACBC =或;ABACBC =或;ABACBC =或().ABC ABC ABC ABC =-++(和A B +即并A B ,当,A B 互斥即AB φ=时,A B 常记为A B +.) 2. 设M 件产品中含m 件次品, 计算从中任取两件至少有一件次品的概率.221M mM C C --或1122(21)(1)m M m m M C C C m M m M M C -+--=- ★3. 从8双不同尺码鞋子中随机取6只, 计算以下事件的概率.A ={8只鞋子均不成双},B ={恰有2只鞋子成双},C ={恰有4只鞋子成双}.61682616()32()0.2238,143C C P A C ===1414872616()80()0.5594,143C C C P B C === 2212862616()30()0.2098.143C C C P C C === ★4. 设某批产品共50件, 其中有5件次品, 现从中任取3件, 求:(1)其中无次品的概率; (2)其中恰有一件次品的概率.(1)34535014190.724.1960C C == (2)21455350990.2526.392C C C ==5. 从1~9九个数字中, 任取3个排成一个三位数, 求:(1)所得三位数为偶数的概率; (2)所得三位数为奇数的概率.(1){P 三位数为偶数}{P =尾数为偶数4},9=(2){P 三位数为奇数}{P =尾数为奇数5},9=或{P 三位数为奇数}1{P =-三位数为偶数45}1.99=-=6. 某办公室10名员工编号从1到10,任选3人记录其号码,求:(1)最小号码为5的概率;(2)最大号码为5的概率.记事件A ={最小号码为5}, B ={最大号码为5}.(1) 253101();12C P A C ==(2) 243101().20C P B C ==7. 袋中有红、黄、白色球各一个,每次从袋中任取一球,记下颜色后放回,共取球三次,求下列事件的概率:A ={全红},B ={颜色全同},C ={颜色全不同},D ={颜色不全同},E ={无黄色球},F ={无红色且无黄色球},G ={全红或全黄}.311(),327P A ==1()3(),9P B P A ==33333!2(),339A P C ===8()1(),9P D P B =-=3328(),327P E ==311(),327P F ==2()2().27P G P A ==☆.某班n 个男生m 个女生(m ≤n +1)随机排成一列, 计算任意两女生均不相邻的概率.☆.在[0, 1]线段上任取两点将线段截成三段, 计算三段可组成三角形的概率. 14第二次作业 1. 设A , B 为随机事件, P (A )=0.92, P (B )=0.93, (|)0.85P B A =, 求:(1)(|)P A B , (2)()P A B ∪. (1) ()()0.85(|),()0.850.080.068,()10.92P AB P AB P B A P AB P A ====⨯=-()()()()()()P AB P A P AB P A P B P AB =-=-+0.920.930.0680.058,=-+=()0.058(|)0.83.()10.93P AB P A B P B ===-(2)()()()()P A B P A P B P AB =+-0.920.930.8620.988.=+-=2. 投两颗骰子,已知两颗骰子点数之和为7,求其中有一颗为1点的概率. 记事件A ={(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)}, B ={(1,6),(6,1)}. 21(|).63P B A ==★.在1—2000中任取一整数, 求取到的整数既不能被5除尽又不能被7除尽的概率. 记事件A ={能被5除尽}, B ={能被7除尽}.4001(),20005P A ==取整2000285,7⎡⎤=⎢⎥⎣⎦28557(),2000400P B ==200057,57⎡⎤=⎢⎥⨯⎣⎦57(),2000P AB = ()()1()1()()()P AB P A B P A B P A P B P AB ==-=--+1575710.686.54002000=--+=3. 由长期统计资料得知, 某一地区在4月份下雨(记作事件A )的概率为4/15, 刮风(用B 表示)的概率为7/15, 既刮风又下雨的概率为1/10, 求P (A |B )、P (B |A )、P (A B ).()1/103(|),()7/1514P AB P A B P B ===()1/103(|),()4/158P AB P B A P A ===()()()()P A B P A P B P AB =+-47119.15151030=+-=4. 设某光学仪器厂制造的透镜第一次落下时摔破的概率是1/2,若第一次落下未摔破,第二次落下时摔破的概率是7/10,若前二次落下未摔破,第三次落下时摔破的概率是9/10,试求落下三次而未摔破的概率.记事件i A ={第i 次落下时摔破},1,2,3.i = 1231213121793()()(|)(|)111.21010200P A A A P A P A A P A A A ⎛⎫⎛⎫⎛⎫==---= ⎪⎪⎪⎝⎭⎝⎭⎝⎭5. 设在n 张彩票中有一张奖券,有3个人参加抽奖,分别求出第一、二、三个人摸到奖券概率.记事件i A ={第i 个人摸到奖券},1,2,3.i =由古典概率直接得1231()()().P A P A P A n ===或212121111()()()(|),1n P A P A A P A P A A n n n-====-31231213121211()()()(|)(|).12n n P A P A A A P A P A A P A A A n n n n--====--或 第一个人中奖概率为11(),P A n=前两人中奖概率为12122()()(),P A A P A P A n +=+=解得21(),P A n=前三人中奖概率为1231233()()()(),P A A A P A P A P A n ++=++=解得31().P A n=6. 甲、乙两人射击, 甲击中的概率为0.8, 乙击中的概率为0.7, 两人同时射击, 假定中靶与否是独立的.求(1)两人都中靶的概率; (2)甲中乙不中的概率; (3)甲不中乙中的概率.记事件A ={甲中靶},B ={乙中靶}.(1) ()()()0.70.70.56,P AB P A P B ==⨯=(2) ()()()0.80.560.24,P AB P A P AB =-=-= (3) ()()()0.70.560.14.P AB P B P AB =-=-=★7. 袋中有a 个红球, b 个黑球, 有放回从袋中摸球, 计算以下事件的概率: (1)A ={在n 次摸球中有k 次摸到红球}; (2)B ={第k 次首次摸到红球};(3)C ={第r 次摸到红球时恰好摸了k 次球}.(1) ();()k n kk n kk k nnna b a b P A C C a b a b a b --⎛⎫⎛⎫== ⎪ ⎪+++⎝⎭⎝⎭(2) 11();()k k kb a ab P B a b a b a b --⎛⎫== ⎪+++⎝⎭ (3) 1111().()rk rr k rr r k k ka b a b P C CCa b a b a b ------⎛⎫⎛⎫== ⎪ ⎪+++⎝⎭⎝⎭8.一射手对一目标独立地射击4次, 已知他至少命中一次的概率为80.81求该射手射击一次命中目标的概率.设射击一次命中目标的概率为,1.p q p =-4801121,,1.818133q q p q =-===-= 9. 设某种高射炮命中目标的概率为0.6, 问至少需要多少门此种高射炮进行射击才能以0.99的概率命中目标.(10.6)10.99,n -<-0.40.01,n <由50.40.01024,=60.40.01,<得 6.n ≥ ☆.证明一般加法(容斥)公式1111()()()()(1)().nn n n i i i i j i j k i i i i ji j kP A P A P A A P A A A P A -===<<<=-+++-∑∑∑证明 只需证分块111,,k k n k i i i i i i A A A A A A +⊂只计算1次概率.(1,,n i i 是1,,n 的一个排列,1,2,,.k n =)分块概率重数为1,,k i i A A 中任取1个-任取2个1(1)k -++-任取k 个,即121(1)1k k k k k C C C --++-=⇔ 121(1)(11)0.k k k k k k C C C -+++-=-=将,互换可得对偶加法(容斥)公式1111()()()()(1)().nnn n i i i ij ij k i i i i ji j kP A P A P A A P AA A P A -===<<<=-+++-∑∑∑☆.证明 若A , B 独立, A , C 独立, 则A , B ∪C 独立的充要条件是A , BC 独立. 证明(())()()()()P A B C P AB AC P AB P AC P ABC ==+- ()()()()()P A P B P A P C P ABC =+- 充分性:⇐(())()()()()(),P A B C P A P B P A P C P ABC =+-代入()()()P ABC P A P BC = ()(()()())P A P B P C P BC =+-()(),P A P B C = 即,A B C 独立. 必要性:⇒(())()()P A B C P A P B C =()(()()())P A P B P C P BC =+-()()()()()()P A P B P A P C P A P BC =+-()()()()()P A P B P A P C P ABC =+- ()()(),P ABC P A P BC =即,A BC 独立.☆.证明:若三个事件A 、B 、C 独立,则A ∪B 、AB 及A -B 都与C 独立. 证明 因为[()]()()()()()()()()()()()[()()()()]()()()P A B C P AC BC P AC P BC P ABC P A P C P B P C P A P B P C P A P B P A P B P C P A B P C ==+-=+-=+-=[()]()()()()[()()]()()()P AB C P ABC P A P B P C P A P B P C P AB P C ==== [()]()()()()()()()()[()()]()()()P A B C P AC B P AC P ABC P A P C P A P B P C P A P AB P C P A B P C -=-=-=-=-=-所以A ∪B 、AB 及A -B 都与C 独立. 第三次作业1. 在做一道有4个答案的选择题时, 如果学生不知道问题的正确答案时就作随机猜测. 设他知道问题的正确答案的概率为p , 分别就p =0.6和p =0.3两种情形求下列事件概率: (1)学生答对该选择题; (2)已知学生答对了选择题,求学生确实知道正确答案的概率. 记事件A ={知道问题正确答案},B ={答对选择题}.(1) 由全概率公式得()()(|)()(|)P B P A P B A P A P B A =+113,444p pp -=+=+ 当0.6p =时,13130.67()0.7,444410p P B ⨯=+=+==当0.3p =时,13130.319()0.475.444440p P B ⨯=+=+== (2) 由贝叶斯公式得()4(|),13()1344P AB p pP A B p P B p ===++当0.6p =时,440.66(|),13130.67p P A B p ⨯===++⨯ 当0.3p =时,440.312(|).13130.319p P A B p ⨯===++⨯ 2. 某单位同时装有两种报警系统A 与B , 当报警系统A 单独使用时, 其有效的概率为0.70; 当报警系统B 单独使用时, 其有效的概率为0.80.在报警系统A 有效的条件下, 报警系统B 有效的概率为0.84.计算以下概率: (1)两种报警系统都有效的概率; (2)在报警系统B 有效的条件下, 报警系统A 有效的概率; (3)两种报警系统都失灵的概率.()0.7,()0.8,(|)0.84.P A P B P B A ===(1) ()()(|)0.70.840.588,P AB P A P B A ==⨯=(2) ()0.588(|)0.735,()0.8P AB P A B P B === (3) ()()1()1()()()P AB P A B P A B P A P B P AB ==-=--+10.70.80.5880.088.=--+=☆.为防止意外, 在矿内同时设有两种报警系统A 与B . 每种系统单独使用时, 其有效的概率系统A 为0. 92, 系统B 为0.93, 在A 失灵的条件下, B 有效的概率为0.85,. 求: (1)发生意外时, 两个报警系统至少有一个有效的概率; (2) B 失灵的条件下, A 有效的概率.3. 设有甲、乙两袋, 甲袋中有n 只白球, m 只红球; 乙袋中有N 只白球, M 只红球. 从甲袋中任取一球放入乙袋, 在从乙袋中任取一球, 问取到白球的概率是多少. 记事件A ={从甲袋中取到白球},B ={从乙袋中取到白球}. 由全概率公式得()()(|)()(|)P B P A P B A P A P B A =+111n N m Nn m N M n m N M +=+++++++().()(1)n N n m n m N M ++=+++☆.设有五个袋子, 其中两个袋子, 每袋有2个白球, 3个黑球. 另外两个袋子, 每袋有1个白球, 4个黑球, 还有一个袋子有4个白球, 1个黑球. (1)从五个袋子中任挑一袋, 并从这袋中任取一球, 求此球为白球的概率. (2)从不同的三个袋中任挑一袋, 并由其中任取一球, 结果是白球, 问这球分别由三个不同的袋子中取出的概率各是多少?★4. 发报台分别以概率0.6和0.4发出信号 “·” 及 “-”. 由于通信系统受到于扰, 当发出信号 “·” 时, 收报台分别以概率0.8及0.2收到信息 “·” 及 “-”; 又当发出信号 “-” 时, 收报台分别以概率0.9及0.l 收到信号 “-” 及 “·”. 求: (1)收报台收到 “·”的概率;(2)收报台收到“-”的概率;(3)当收报台收到 “·” 时, 发报台确系发出信号 “·” 的概率;(4)收到 “-” 时, 确系发出 “-” 的概率.记事件B ={收到信号 “·”},1A ={发出信号 “·”},2A ={发出信号“-”}. (1) )|()()|()()(2211A B P A P A B P A P B P +=;52.01.04.0)2.01(6.0=⨯+-⨯= (2) ()1()10.520.48;P B P B =-=-=(3) 1111()()(|)(|)()()P A B P A P B A P A B P B P B ==0.60.8120.923;0.5213⨯=== (4)2222()()(|)(|)()()P A B P A P B A P A B P B P B ==0.40.930.75.0.484⨯=== 5. 对以往数据分析结果表明, 当机器调整良好时, 产品合格率为90%, 而机器发生某一故障时, 产品合格率为30%. 每天早上机器开动时, 机器调整良好的概率为75%. (1)求机器产品合格率,(2)已知某日早上第一件产品是合格品, 求机器调整良好的概率. 记事件B ={产品合格},A ={机器调整良好}. (1) 由全概率公式得()()(|)()(|)P B P A P B A P A P B A =+0.750.90.250.30.75,=⨯+⨯= (2) 由贝叶斯公式得()()(|)(|)()()P AB P A P B A P A B P B P B ==0.750.90.9.0.75⨯== ☆.系统(A), (B), (C)图如下, 系统(A), (B)由4个元件组成, 系统(C)由5个元件组成,每个元件的可靠性为p , 即元件正常工作的概率为p , 试求整个系统的可靠性.(A) (B) (C) 记事件A ={元件5正常},B ={系统正常}.(A) 222(|)(1(1)(1))(44),P B A p p p p p =---=-+ (B) 2222(|)1(1)(1)(2),P B A p p p p =---=- (C) 由全概率公式得()()(|)()(|)P B P A P B A P A P B A =+2222(44)(1)(2)p p p p p p p =⋅-++-- 23452252.p p p p =+-+第四次作业1. 在15个同型零件中有2个次品, 从中任取3个, 以X 表示取出的次品的个数, 求X 的分布律.2213315(),0,1,2.k k C C P X k k C -===☆.经销一批水果, 第一天售出的概率是0.5, 每公斤获利8元, 第二天售出的概率是0.4, 每公斤获利5元, 第三天售出的概率是0.1, 每公斤亏损3元. 求经销这批水果每公斤赢利X0,3,(3)(3)0.1,35,()(5)(3)(5)0.10.40.5,58,(8)1,8.x F P X x F x F P X P X x F x <-⎧⎪-==-=-≤<⎪=⎨==-+==+=≤<⎪⎪=≥⎩2. 抛掷一枚不均匀的硬币, 每次出现正面的概率为2/3, 连续抛掷8次, 以X 表示出现正面的次数, 求X 的分布律.(8,2/3),X B n p ==8821(),0,1,,8.33k kk P X k C k -⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭3. 一射击运动员的击中靶心的命中率为0.35, 以X 表示他首次击中靶心时累计已射击的次数, 写出X 的分布律, 并计算X 取偶数的概率.(0.35),X G p =11()0.350.65,1,2.k k P X k pq k --===⨯= ()+()=1,()()=,P X P X P X P X q ⎧⎪⎨⎪⎩奇偶偶奇 解得0.6513()=0.394.110.6533q P X q ==++偶4. 一商业大厅里装有4个同类型的银行刷卡机, 调查表明在任一时刻每个刷卡机使用的概率为0.1,求在同一时刻:(1)恰有2个刷卡机被使用的概率;(2)至少有3个刷卡机被使用的概率; (3)至多有3个刷卡机被使用的概率;(4)至少有一个刷卡机被使用的概率. 在同一时刻刷卡机被使用的个数(4,0.1).X B n p ==(1) 2224(2)0.10.90.00486,P X C ==⨯⨯= (2) 3344(3)(3)(4)0.10.90.10.0037,P X P X P X C ≥==+==⨯⨯+= (3) 4(3)1(4)10.10.9999,P X P X ≤=-==-=(4)4(1)1(0)10.910.65610.3439.P X P X ≥=-==-=-=5. 某汽车从起点驶出时有40名乘客, 设沿途共有4个停靠站, 且该车只下不上. 每个乘客在每个站下车的概率相等, 并且相互独立, 试求: (1)全在终点站下车的概率; (2)至少有2个乘客在终点站下车的概率; (3)该车驶过2个停靠站后乘客人数降为20的概率. 记事件A ={任一乘客在终点站下车},乘客在终点站下车人数(40,1/4).X B n p ==(1) 40231(40)8.271810,4P X -⎛⎫===⨯ ⎪⎝⎭(2) 403940140313433(2)1(0)(1)1144434P X P X P X C ⎛⎫⎛⎫⎛⎫≥=-=-==--⨯=-⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭10.0001340880.999865912.=-=(3) 记事件B ={任一乘客在后两站下车},乘客在后两站下车人数(40,1/2).Y B n p ==2020202040404011(20)0.1268.222C P Y C ⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭(精确值)应用斯特林公式!2,nn n n e π⎛⎫ ⎪⎝⎭2020202040404011(20)222C P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭24040!(20!)2= 402204040202e e ⎫⎪⎝⎭⎫⎫⎪⎪⎪⎭⎭0.1262.=其中 1.7724538509.π==参:贝努利分布的正态近似.6. 已知瓷器在运输过程中受损的概率是0.002, 有2000件瓷器运到, 求: (1)恰有2个受损的概率; (2)小于2个受损的概率; (3)多于2个受损的概率; (4)至少有1个受损的概率.受损瓷器件数(2000,0.002),X B n p ==近似为泊松分布(4).P n p λ=⨯=(1) 2441480.146525,2!P e e --=== (2) 4424150.0915782,1!P e e --⎛⎫=+== ⎪⎝⎭(3) 431211130.761897,P P P e-=--=-= (4) 4410.981684.P e -=-=7. 某产品表面上疵点的个数X 服从参数为1.2的泊松分布, 规定表面上疵点的个数不超过2个为合格品, 求产品的合格品率.产品合格品率2 1.2 1.21.2 1.212.920.879487.1!2!P e e --⎛⎫=+=== ⎪⎝⎭ ★8. 设随机变量X求:X 的分布函数, 以及概率(||5).X ≤ 随机变量X 的分布函数为0,3,(3)(3)0.2,35,()(5)(3)(5)0.20.50.7,58,(8)1,8.x F P X x F x F P X P X x F x <-⎧⎪-==-=-≤<⎪=⎨==-+==+=≤<⎪⎪=≥⎩(36)(5)0.5,P X P X <≤===(1)(5)(8)0.50.30.8,P X P X P X >==+==+=(5)(||5)(5)(3)(5)0.20.50.7,P X P X F P X P X ≤=≤===-+==+=第五次作业1. 学生完成一道作业的时间X 是一个随机变量(单位: 小时), 其密度函数是2,00.5()0,kx x x f x ⎧+≤≤=⎨⎩其他试求: (1)系数k ; (2)X 的分布函数; (3)在15分钟内完成一道作业的概率; (4)在10到20分钟之间完成一道作业的概率. (1) 0.50.523200111(0.5),21,32248kk F kx xdx x x k ⎛⎫==+=+=+= ⎪⎝⎭⎰(2) 23200,01()()217,00.5,2(0.5)1,0.5.x x F x P X x x xdx x x x F x <⎧⎪⎪=≤=+=+≤<⎨⎪=≥⎪⎩⎰(3) 322011119()2170.140625,442464x F P X x x xdx ⎛⎫⎛⎫⎛⎫=≤=+=+== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰(4) 3212316111111129217.6336424108P X F F x xdx ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫≤≤=-=+=+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎰2. 设连续型随机变量X 服从区间[-a , a ](a >0)上的均匀分布, 且已知概率1(1)3P X >=, 求: (1)常数a ; (2)概率1()3P X <.(1) 1111(1),3,223aa P X dx a a a ->====⎰(2) 13311115()3.36639P X dx -⎛⎫<==+= ⎪⎝⎭⎰3. 设某元件的寿命X 服从参数为θ 的指数分布, 且已知概率P (X >50)=e -4, 试求:(1)参数θ 的值; (2)概率P (25<X <100) . 补分布()()|,0.x x xx x S x P X x e dx e ex θθθθ+∞--+∞->==-=>⎰ (1) 504502(50)(50),0.08,25x S P X e dx e e θθθθ+∞---=>=====⎰(2) 由()(),,0,rxr S rx e S x r x θ-==>取50,x =依次令1,2,2r =得12282(25)(25)(50),(100)(100)(50)S P X S e S P X S e --=>===>==0.0003354563,=其中 2.7182818284.e28(25100)(25)(100)P X P X P X e e --<<=>->=- 0.135334650.00033545630.1349991937.=-= 4. 某种型号灯泡的使用寿命X (小时)服从参数为1800的指数分布, 求: (1)任取1只灯泡使用时间超过1200小时的概率; (2)任取3只灯泡各使用时间都超过1200小时的概率. (1) 1312008002(1200)0.2231301602,P X ee -⨯->===1.6487212707001.= (2) 932(1200)0.0111089965.P X e->==5. 设X ~N (0, 1), 求: P (X <0.61), P (-2.62<X <1.25), P (X ≥1.34), P (|X |>2.13). (1) (0.61)(0.61)0.72907,P X <=Φ=(2) ( 2.62 1.25)(1.25)( 2.62)(1.25)(2.62)1P X -<<=Φ-Φ-=Φ+Φ-0.894359956010.88995,=+-=(3) ( 1.34)1(1.34)10.909880.09012,P X >=-Φ=-= (4)(|| 2.13)22(2.13)220.983410.03318.P X >=-Φ=-⨯=6. 飞机从甲地飞到乙地的飞行时间X ~N (4, 19). 设飞机上午10: 10从甲地起飞, 求: (1)飞机下午2: 30以后到达乙地的概率; (2)飞机下午2: 10以前到达乙地的概率; (3)飞机在下午1: 40至2: 20之间到达乙地的概率.(1) 131331/34111(1)10.841340.15866,331/3P X P X -⎛⎫⎛⎫⎛⎫>=-≤=-Φ=-Φ=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2) (4)(0)0.5,P X <=Φ=(3) 72525/647/24261/31/3P X --⎛⎫⎛⎫⎛⎫<<=Φ-Φ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭13122⎛⎫⎛⎫=Φ+Φ- ⎪ ⎪⎝⎭⎝⎭0.691460.9331910.62465.=+-=★7. 设某校高三女学生的身高X ~N (162, 25), 求: (1)从中任取1个女学生, 求其身高超过165的概率; (2)从中任取1个女学生, 求其身高与162的差的绝对值小于5的概率; (3)从中任取6个女学生, 求其中至少有2个身高超过165的概率.(1) 162165162(165)0.61(0.6)10.72580.2742,55X P X P --⎛⎫>=>==-Φ=-=⎪⎝⎭ (2) 162(|162|5)12(1)120.8413410.6827,5X P X P ⎛-⎫-<=<=Φ-=⨯-= ⎪⎝⎭(3) 记事件A ={任一女生身高超过165}, ()(165)0.2742,p P A P X ==>= 随机变量Y 贝努利分布(6,0.2742),B n p ==6156(2)1(0)(1)1(1)(1)0.52257.P Y P Y P Y p C p p ≥=-=-==----=第六次作业★1.设随机变量X 的分布律为(1)求Y =|X |的分布律; (2)求Y =X 2+X 的分布律. (1)(2)★.定理X 密度为()X f x ,()y g x =严格单调,反函数()x x y =导数连续,则()Y g X =是连续型变量,密度为(())|()|,()(),()0,XY f x y x y g x y g x f y αβ'=<<=⎧=⎨⎩极小值极大值其它. 证明 1)若()0,x x y ''=>{}{()()}{},Y y g X g x X x ≤=≤=≤()()(()())()(),Y X F y P Y y P g X g x P X x F x =≤=≤=≤= 两边对y 求导,()(())(),.Y X f y f x y x y y αβ'=<<2)若()0,x x y ''=<{}{()()}{},Y y g X g x X x ≤=≤=≥()()(()())()1(),Y X F y P Y y P g X g x P X x F x =≤=≤=≥=- 两边对y 求导,()(())(),.Y X f y f x y x y y αβ'=-<<因此总有()(())|()|,.Y X f y f x y x y y αβ'=<< 或证明()(),()0,()()(()())()1(),()0,X Y X P X x F x g x F y P Y y P g X g x P X x F x g x '≤=>⎧=≤=≤=⎨'≥=-<⎩ 两边对y 求导,(),()(),X Y X dF x dxdx dyf y dF x dx dx dy ⎧⎪⎪=⎨⎪-⎪⎩或两边微分()(),()()()(),X X Y Y X XdF x f x dx dF y f y dy dF x f x dx =⎧==⎨-=-⎩(),()(),X Y X dx f x dy f y dxf x dy ⎧⎪=⎨-⎪⎩(())|()|,.X f x y x y y αβ'=<<2. 设随机变量X 的密度函数是f X (x ), 求下列随机变量函数的密度函数: (1)Y =tan X ; (2)1Y X=; (3)Y =|X |. (1) 反函数()arctan ,x y y ='21(),1x y y =+由连续型随机变量函数的密度公式得'21()(())|()|(arctan ).1Y X Xf y f x y x y f y y ==+ 或 反函数支()arctan ,i x y i y i π=+为整数,'21(),1i x y y =+ '21()(())|()|(arctan ).1Y X i iX i i f y f x y x y f i y y π+∞+∞=-∞=-∞==++∑∑(2) 1,X Y =反函数1,y x y ='211()()().Y X y y X f y f x x f y y==(3) ()()(||)()()()Y X X F y P Y y P X y P y X y F y F y =≤=≤=-≤≤=--. 两边对y 求导得Y 的密度函数为()()(),0.Y X X f y f y f y y =+->★3. 设随机变量X ~U [-2, 2], 求Y =4X 2-1的密度函数.2()()(41)(115,Y F y P Y y P X y P X y =≤=-≤=≤=-≤≤两边对y 求导得随机变量Y 的密度为()115.Y f y y =-≤≤ 或解反函数支12()()x y x y =='''112211()(())|()|(())|()|2(())()115.Y X X X f y f x y x y f x y x y f x y x y y =+==-≤≤★4. 设随机变量X 服从参数为1的指数分布, 求Y =X 2的密度函数(Weibull 分布). 当0y ≤时, 2Y X =的分布()0Y F y =,当0y >时,2()()()(Y X F y P Y y P X y P X F =≤=≤=≤= 两边对y 求导得()Y X f y f '==0,()0.Y y f y >=⎩或反函数y x='()()0.Y X y y f y f x x y ==>★5. 设随机变量X~N (0, 1), 求(1)Y =e X 的密度函数; (2)Y =X 2的密度函数(Gamma 分布). (1) 当0y ≤时, e X Y =的分布()0Y F y =,当0y >时,()()(e )(ln )(ln ),X Y F y P Y y P y P X y y =≤=≤=≤=Φ 因而Y 的密度为''1()(ln )(ln )(ln )(ln ),Y f y y y y y y ϕϕ=Φ=={}2(ln ),0,2()0,0.Y y y f y y ->=≤⎩ 或 反函数ln ,X Y =ln ,y x y ='1()()(ln )Y y y f y x x y y ϕϕ=={}2(ln ),0.2y y =-> (2) 当0y ≤时,()0Y F y =;当0Y >时,2()()()((Y X X F y P Y y P X y P X F F =≤=≤=≤≤=-.两边对y 求导得Y的密度函数为2,0,()0.yY y f y ->=⎩或反函数支12()()x y x y =''21122()(())|()|(())|()|,0.yY X X f y f x y x y f x y x y y -=+=>6. 设随机变量X 的密度函数是21,1()0,1X x f x x x ⎧>⎪=⎨⎪≤⎩, 求Y =ln X 的概率密度. 反函数,y y x e ='()()(),0.y y y Y X y y X f y f x x f e e e y -===>第七次作业☆.将8个球随机地丢入编号为1, 2, 3, 4, 5的五个盒子中去, 设X 为落入1号盒的球的个数, Y 为落入2号盒的球的个数, 试求X 和Y 的联合分布律.1. 袋中装有标上号码1, 2, 2的3个球, 从中任取一个并且不再放回, 然后再从袋中任取一球,. 以X , Y 分别记第一、二次取到球上的号码数, 求: (1)(X , Y )的联合分布律(设袋中各球被取机会相等); (2)X , Y 的边缘分布律; (3)X 与Y 是否独立? (1)(X , Y )的联合分布律为(1,1)0,P X Y ===1(1,2)(2,1)(2,2).3P X Y P X Y P X Y =========(2) X , Y 的分布律相同,12(1),(2).33P X P X ====(3) X 与Y 不独立.2. 设二维连续型变量(,)X Y 的联合分布函数35(1)(1),,0,(,)0,.x y e e x y F x y --⎧-->=⎨⎩其它求(,)X Y 联合密度.2(,)(,),f x y F x y x y ∂=∂∂3515,,0,(,)0,.x y e x y f x y --⎧>=⎨⎩其它★3. 设二维随机变量(X , Y )服从D 上的均匀分布, 其中D 是抛物线y =x 2和x =y 2所围成的区域, 试求它的联合密度函数和边缘分布密度函数, 并判断Y X ,是否独立.分布区域面积213123200211,333x S x dx x x ⎛⎫==-=-= ⎪⎝⎭⎰⎰联合密度213,1,(,)0,.x y f x y S ⎧=<<<⎪=⎨⎪⎩其它边缘X的密度为22()),01,X xf x dy x x ==-<<边缘Y的密度为22()),0 1.Y yf y dy y y ==<<(,)()(),X Y f x y f x f y ≠⋅因此X 与Y 不独立.或(,)f x y 非零密度分布范围不是定义在矩形区域上,因此X 与Y 不独立.4. 设二维离散型变量),(Y X 联合分布列是问,p q 取何值时X 与Y两行成比例1/151/52,1/53/103q p ===解得12,.1015p q ==★5.设(,)X Y 的联合密度为2,11,0,(,)0,.y Ax e x y f x y -⎧-<<>=⎨⎩其它求:(1)常数A ;(2)概率1(0,1);2P X Y <<>(3)边缘概率密度f X (x ), f Y (y ); (4)X 与Y 是否相互独立? (1) 2220()(,),11,y y X f x f x y dy Ax e dy Ax e dy Ax x +∞+∞+∞--====-<<⎰⎰⎰112112()1,3X f x dx Ax dx A --===⎰⎰3.2A = (2) 112201113(0,1)(0)(1).22216ye P X Y P X P Y x dx e dy -+∞-<<>=<<>==⎰⎰ (3) 23(),11,2X f x x x =-<<111221113()(,),0.2y yy Y f y f x y dx Ax e dx e x dx e y ------====>⎰⎰⎰(4)由23,11,0()()(,),20,yX Y x e x y f x f y f x y -⎧-<<>⎪⋅==⎨⎪⎩其它得X 与Y 独立. 或因为2(,),11,0,y f x y Ax e x y -=-<<>可表示为x 的函数与y 的函数的积且分布在矩形区域上,所以X 与Y 相互独立.由此得(),0;y Y f y e y -=>2(),11,X f x Ax x =-<<112112()1,3X f x dx Ax dx A --===⎰⎰3.2A = 112201113(0,1)(0)(1).22216y e P X Y P X P Y x dx e dy -+∞-<<>=<<>==⎰⎰6. 设X 服从均匀分布(0,0.2),U Y 的密度为55,0,()0,y Y e y f y -⎧>=⎨⎩其它.且,X Y 独立.求:(1)X的密度;(2) (,)X Y 的联合密度. (1)X 的密度为()5,00.2,X f x x =≤≤(2)(,)X Y 的联合密度为525,00.2,0,(,)0,y e x y f x y -⎧≤≤>=⎨⎩其它.第八次作业★1.求函数(1)Z 1=X +Y , (2) Z 2=min{X , Y }, (3) Z 3=max{X , Y }的分布律.(1) 11(0)(0),6P Z P X Y =====1111(1)(0,1)(1,0),362P Z P X Y P X Y ====+===+=1111(2)(0,2)(1,1),12126P Z P X Y P X Y ====+===+=11(3)(1,2).6P Z P X Y =====(2) 2111(1)(1,1)(1,2),1264P Z P X Y P X Y ====+===+=223(0)1(1).4P Z P Z ==-==(3) 31(0)(0),6P Z P X Y =====31117(1)(0,1)(1,1)(1,0),312612P Z P X Y P X Y P X Y ====+==+===++=3111(2)(0,2)(1,2).1264P Z P X Y P X Y ====+===+=2. 设随机变量(求函数Z =X /Y 的分布律.(/1)(1)(1)0.250.250.5,P Z X Y P X Y P X Y =====+==-=+= (/1)1(/1)0.5.P Z X Y P Z X Y ==-=-===3. 设X 与Y 相互独立, 概率密度分别为220()00,xX e x f x x -⎧>=⎨≤⎩0()00,y Y e y f y x -⎧>=⎨≤⎩试求Z =X +Y 的概率密度.()(,)()()zzZ X Y f z f x z x dx f x f z x dx =-=-⎰⎰20222(1),0.z zx z x z x z z e e dx e e dx e e z --+----===->⎰⎰★4. 设X ~U (0, 1), Y ~E (1), 且X 与Y 独立, 求函数Z =X +Y 的密度函数.,01,0,(,)0,y e x y f x y -⎧<<>=⎨⎩其它,当01z <≤时,()(,)()()zzZ X Y f z f x z x dx f x f z x dx =-=-⎰⎰01,zz z x z xz x e dx e e -+-+-====-⎰当1z >时,11110()(,)()().zz x z xz z Z X Y x f z f x z x dx f x f z x dx e dx e e e -+-+--==-=-===-⎰⎰⎰因此11,01,(),1,0,.z z z Z e z f z e e z ---⎧-≤≤⎪=->⎨⎪⎩其它★5. 设随机变量(X , Y )的概率密度为()101,0(,)10x y e x y f x y e -+-⎧⎪<<<<+∞=⎨-⎪⎩其它(1)求边缘概率密度f X (x ), f Y (y ); (2)求函数U =max (X , Y )的分布函数; (3)求函数V =min(X , Y )的分布函数.(1) 1,01,()10,xX e x f x e --⎧<<⎪=-⎨⎪⎩其它.,0,()0,y Y e y f y -⎧>=⎨⎩其它. (2) 11000,0,1()(),01,111,1xx x x X X x e e F x f x dx dx x e e x ----≤⎧⎪-⎪===<<⎨--⎪≥⎪⎩⎰⎰.min{,1}10,0,1,01x x e x e --≤⎧⎪=⎨->⎪-⎩. 0,0,()1,0Y yy F y e y -≤⎧=⎨->⎩.21(1),01,()()()11,1x U X Y x e x F x F x F x e e x ---⎧-<<⎪==-⎨⎪-≥⎩. min{,1}1(1)(1),0.1x x e e x e -----=>-(3) 111,0,()1(),01,10,1x X X x e eS x F x x e x ---≤⎧⎪-⎪-=<<⎨-⎪≥⎪⎩.min{,1}111,0,,01x x e e x e---≤⎧⎪=⎨->⎪-⎩.1,0,()1(),0Y Y yy S y F y e y -≤⎧-=⎨>⎩.112111()11,01,()1()()111,1x x x xV X Y e e e e e e x F x S x S x e e x ---------⎧---+-=<<⎪=-=--⎨⎪≥⎩. 1min{,1}111,01x x x e e e x e --------+=>-.6. 设某种型号的电子管的寿命(以小时计)近似地服从N (160, 202)分布. 随机地选取4只求其中没有一只寿命小于180小时的概率.随机变量2(160,20),X N 180160(180)(1)0.84134,20P X -⎛⎫≤=Φ=Φ= ⎪⎝⎭没有一只寿命小于180小时的概率为444(180)(1(1))(10.84134)0.00063368.P X >=-Φ=-=第九次作业★1.试求: E (X ), E (X 2+5), E (|X |).20.110.210.320.130.10.4,i i iEX x p ==-⨯-⨯+⨯+⨯+⨯=∑2222222(2)0.1(1)0.210.320.130.1 2.2,i i iEX x p ==-⨯+-⨯+⨯+⨯+⨯=∑22(5)57.2,E X EX +=+=||||20.110.210.320.130.1 1.2.i i iE X x p ==⨯+⨯+⨯+⨯+⨯=∑2. 设随机变量X 的概率密度为0 0,() 01, 1.x x f x x x Ae x -⎧≤⎪=<≤⎨⎪>⎩求: (1)常数A ; (2)X 的数学期望.(1) 1100111(),2x f x dx xdx Ae dx Ae +∞+∞--==+=+⎰⎰⎰,2e A =(2) 12100114()2.2323x e e EX xf x dx x dx xe dx e +∞+∞--==+=+⨯=⎰⎰⎰★3. 设球的直径D 在[a , b ]上均匀分布,试求: (1)球的表面积的数学期望(表面积2D π);(2)球的体积的数学期望(体积316D π).(1) 22222()();3ba x E D ED dx a ab b b a ππππ===++-⎰ (2) 33322()().6624b a x E D ED dx a b a b b a ππππ⎛⎫===++ ⎪-⎝⎭⎰ ★4. 设二维离散型随机变量(X , Y )的联合分布律为求E (X ), E (Y ), E (XY ).2(0.10.050.050.1)2(0.10.150.050.1)i i iEX x p ==-⨯++++⨯+++∑20.320.350.1,=-⨯+⨯=1(0.10.050.1)2(0.050.15)j j jEY y p ==⨯+++⨯+∑3(0.050.10.05)4(0.10.20.05) 2.65,+⨯+++⨯++=,()i j i j ijE XY x y p =∑∑2(10.120.0530.0540.01)2(10.120.1530.0540.05)=-⨯⨯+⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯ 1.5 1.50.=-+=★5. 设随机变量X 和Y 独立, 且具有概率密度为2,01,()0,X x x f x <<⎧=⎨⎩其它,3(1)3,1,()0, 1.y Y ey f y y --⎧>=⎨≤⎩(1)求(25)E X Y +; (2)求2()E X Y .(1) 112002()2,3X EX xf x dx x dx ===⎰⎰3(1)114()3,3y Y EY yf y dy ye dy +∞+∞--===⎰⎰或随机变量1Z Y =-指数分布(3),E 141,,33EZ EY EY =-==24(25)25258.33E X Y EX EY +=+=⨯+⨯=(2) 11223001()2,2X EX x f x dx x dx ===⎰⎰由X 和Y 独立得22142().233E X Y EX EY ==⨯=第十次作业1. 设离散型随机变量试求: (1) D (X ); (2) D (-3X +2) .(1) 20.110.210.320.130.10.4,i i iEX x p ==-⨯-⨯+⨯+⨯+⨯=∑2222222(2)0.1(1)0.210.320.130.1 2.2,i i iEX x p ==-⨯+-⨯+⨯+⨯+⨯=∑2222.20.4 2.04.DX EX E X =-=-=(2) 2(32)(3)9 2.0418.36.D X DX -+=-=⨯=★2. 设随机变量X 具有概率密度为22,02,()0,Ax x x f x ⎧+<<=⎨⎩其他,试求: (1)常数A ; (2)E (X ); (3) D (X ); (4) D (2X -3) .(1) 22081()(2)4,3f x dx Ax x dx A +∞-∞==+=+⎰⎰解得9.8A =-(2) 22095()(2).86EX xf x dx x x x dx +∞-∞==-+=⎰⎰(3) 22222094()(2),85EX x f x dx x x x dx +∞-∞==-+=⎰⎰2224519.56180DX EX E X ⎛⎫=-=-= ⎪⎝⎭(4) 21919(23)24.18045D X DX -==⨯=★3. 设二维随机变量(,)X Y 联合概率密度为2,01,01,(,)0,x y x y f x y --<<<<⎧=⎨⎩其他,试求: (1),X Y 的协方差和相关系数A ; (2)(21).D X Y -+(1) 103()(,)(2),01,2X f x f x y dy x y dy x x +∞-∞==--=-<<⎰⎰由,x y 的对称性3(),0 1.2Y f y y y =-<<1035(),212X EX xf x dx x x dx EY +∞-∞⎛⎫==-== ⎪⎝⎭⎰⎰12222031(),24X EX x f x dx x x dx EY +∞-∞⎛⎫==-== ⎪⎝⎭⎰⎰2221511,412144DX EX E X DY ⎛⎫=-=-== ⎪⎝⎭11001()(,)(2),6E XY xyf x y dydx xy x y dydx +∞+∞-∞-∞==--=⎰⎰⎰⎰ 因此2151(,)(),612144Cov X Y E XY EXEY ⎛⎫=-=-=- ⎪⎝⎭,1.11X Y ρ==-(2) 由随机变量和的方差公式()2(,)D X Y DX DX Cov X Y +=++得(21)(2)()2(2,)D X Y D X D Y Cov X Y -+=+-+-22592(1)22(1)(,).144DX DY Cov X Y =+-+⨯⨯-⨯=★4. 设二维随机变量(,)X Y 具有联合分布律试求,,,EX DX EY DY 以及X 和Y 的相关系数. (1) X 的分布列为0.45由变量X 分布对称得0,EX =或10.4500.4510.450,i i iEX x p ==-⨯+⨯+⨯=∑22222(1)0.4500.4510.450.9,i i iEX x p ==-⨯+⨯+⨯=∑220.9.DX EX E X =-=(2) Y 的分布列为j (,)X Y 取值关于原点中心对称由变量Y 分布对称得0,EY =或20.20.250.2520.20,j j iEY y p ==-⨯-++⨯=∑222222(2)0.2(1)0.2510.2520.2 2.1,j j iEY y p ==-⨯+-⨯+⨯+⨯=∑22 2.1.DY EY E Y =-=(3) 由二维变量(,)X Y 的联合分布列关于两坐标轴对称得,()0,i j i j ijE XY x y p ==∑∑(,)()0,Cov X Y E XY EXEY =-=因此,0.X Y ρ==5. 设随机变量X 服从参数为2的泊松分布(2)P ,随机变量Y 服从区间(0,6)上的均匀分布(0,6),U 且,X Y 的相关系数,X Y ρ=记2,Z X Y =-求,.EZ DZ (1) 2,EX =063,2EY +==(2)2223 4.EZ E X Y EX EY =-=-=-⨯=-(2) 2(60)2, 3.12DX DY -===由,X Y ρ==得(,)1,Cov X Y = 由随机变量和的方差公式()2(,)D X Y DX DY Cov X Y +=++得2(2)(2)2(,2)(2)4(,)10.DZ D X Y DX D Y Cov X Y DX DY Cov X Y =-=+-+-=+--=第十一次作业★1. 试用切比雪夫不等式估计下一事件概率至少有多大: 掷1000次均匀硬币, 出现正面的次数在400到600次之间.出现正面的次数~(1000,0.5),X B n p == 10000.5500,EX np ==⨯=10000.50.5250,DX npq ==⨯⨯=应用切比雪夫不等式,有239(400600)(|500|100)1.10040DX P X P X ≤≤=-≤≥-=2. 若每次射击目标命中的概率为0.1, 不断地对靶进行射击, 求在500次射击中, 击中目标的次数在区间(49, 55)内的概率.击中目标的次数~(500,0.1),X B n p ==5000.150,EX np ==⨯=5000.10.945.DX npq ==⨯⨯= 根据中心极限定理,X 近似服从正态分布(50,45).N EX DX ==(4955)P X P ≤≤=≤≤1≈Φ-Φ=Φ+Φ-⎝⎭⎝⎭ (0.74)(0.15)10.77040.559610.33.=Φ+Φ-=+-=★3. 计算器在进行加法时, 将每个加数舍入最靠近它的整数.设所有舍入误差是独立的且在(-0.5, 0.5)上服从均匀分布, (1)若将1500个数相加, 问误差总和的绝对值超过15的概率是多少?(2)最多可有几个数相加使得误差总和的绝对值小于10的概率不小于0.90.(1) 误差变量,1,2,.i X i =⋅⋅⋅独立同均匀分布(0.5,0.5),X U -10,.12EX DX ==由独立变量方差的可加性150011500125,12i i D X =⎛⎫== ⎪⎝⎭∑15001i i X =∑近似(0,125).N15001||15i i P X =⎧⎫>⎨⎬⎩⎭∑15001|ii P X =⎧⎪=>=⎨⎪⎪⎩⎭∑2222(1.34)220.90990.1802.≈-Φ=-Φ=-⨯=⎝⎭(2) 1||10n i i P X =⎧⎫<⎨⎬⎩⎭∑1||n i P X =⎧⎪=<=⎨⎪⎩210.90,⎛≈Φ-≥ ⎝0.95,⎛Φ≥ ⎝1.645,≥2124.4345.1.645n ≤= 因此,最多可有4个数相加,误差总和的绝对值小于10的概率不小于0.90.★4. 一个系统由n 个相互独立的部件所组成, 每个部件的可靠性(即部件正常工作的概率)为0.90. 至少有80%的部件正常工作才能使整个系统正常运行, 问n 至少为多大才能使系统正常运行的可靠性不低于0.95.正常工作的部件数~(,),X B n p 其中0.9.p =0.9,EX np n ==0.09.DX npq n ==(0.8)P X n≥3P ⎛=≥==-⎭0.95,3⎛≈Φ≥ ⎝⎭1.645,24.354.n ≥≥因此n 至少取25.★5. 有一大批电子元件装箱运往外地, 正品率为0.8, 为保证以0.95的概率使箱内正品数多于1000只, 问箱内至少要装多少只元件?正品数~(,),X B n p 其中0.8.p =0.8,EX np n ==0.16.DX npq n ==(1000)P X≥P =≥=0.95,≈Φ≥1.645,0.810000.n ≥-≥ 解得1637.65,n ≥因此n 至少取1638.★.贝努利分布的正态近似.投掷一枚均匀硬币40次出现正面次数20X =的概率. 正面次数(40,1/2),X B n p ==400.520,400.50.510.EX np DX npq ==⨯===⨯⨯= 离散值20X =近似为连续分组区间19.520.5,X <<(20)(19.520.5)P X P X =<<0.16P ⎫=<=⎪⎭2((0.16)0.5)2(0.56360.5)0.1272.=Φ-=⨯-= 第十二次作业★1. 设X 1, X 2, ⋅⋅⋅, X 10为来自N (0, 0.32)的一个样本, 求概率1021{ 1.44}i i P X =>∑.标准化变量(0,1),1,2,...,10.0.3iXN i =由卡方分布的定义,10222211~(10).0.3ii Xχχ==∑1021 1.44i i P X =⎧⎫>⎨⎬⎩⎭∑10222211 1.44(10)160.1,0.30.3i i P X χ=⎧⎫==>=≈⎨⎬⎩⎭∑ 略大,卡方分布上侧分位数20.1(10)15.9872.χ= ★2. 设X 1, X 2, X 3, X 4, X 5是来自正态总体X ~(0, 1)容量为5的样本, 试求常数c , 使得统计量t 分布, 并求其自由度.由独立正态分布的可加性,12(0,2),X X N +标准化变量(0,1),U N =由卡方分布的定义,22222345~(3),X X X χχ=++U 与2χ独立.由t 分布的定义,(3),T t ===因此c =自由度为3.★3. 设112,,,n X X X 为来自N (μ1, σ2)的样本, 212,,,nY Y Y 为来自N (μ2, σ2)的样本, 且两样本相互独立, 2212,S S 分别为两个样本方差, 222112212(1)(1)2pn S n S S n n -+-=+-. 试证明22().p E S σ=证 由221112(1)~(1),n S n χσ--及()211(1)1E n n χ-=-得()2211112(1)(1)1,n S E E n n χσ⎛⎫-=-=- ⎪⎝⎭221.ES σ= 类似地222.ES σ=222112212(1)(1)2pn S n S ES E n n ⎛⎫-+-= ⎪+-⎝⎭22212121212(1)(1).22n n ES ES n n n n σ--=+=+-+-。


对错参考答案:√
对错参考答案:×
对错参考答案:√
对错参考答案:√
对错参考答案:√
对错参考答案:×
对错参考答案:×
对错参考答案:√
对错参考答案:√
对错参考答案:×
对错参考答案:×
对错参考答案:√
对错参考答案:×
对错参考答案:√
对错参考答案:√
对错参考答案:√
对错参考答案:√
对错参考答案:√
对错参考答案:×
对错参考答案:√
对错参考答案:√
对错参考答案:√
对错参考答案:√
对错参考答案:×
对错参考答案:×
对错参考答案:×
对错参考答案:√
对错参考答案:×
对错参考答案:×
对错参考答案:×
对错参考答案:√
对错参考答案:×
对错参考答案:√
对错参考答案:√
对错参考答案:√
对错参考答案:×
对错参考答案:×
对错参考答案:√
对错参考答案:√
对错参考答案:×。

数理统计第一次作业1、设总体X 服从正态分布),(2σμN ,其中μ已知,2σ未知,n X X X ,,,21 为其样本,2≥n ,则下列说法中正确的是(D )。
(A )∑=-ni iXn122)(μσ是统计量 (B )∑=ni iXn122σ是统计量(C )∑=--ni i X n 122)(1μσ是统计量 (D )∑=ni i X n12μ是统计量2、设两独立随机变量)1,0(~N X ,)9(~2χY ,则YX 3服从(C )。
)(A )1,0(N )(B )3(t )(C )9(t )(D )9,1(F3、设两独立随机变量)1,0(~N X ,2~(16)Y χ服从( C )。
)(A )1,0(N )(B (4)t )(C (16)t )(D (1,4)F4、设n X X ,,1 是来自总体X 的样本,且μ=EX ,则下列是μ的无偏估计的是( A ).)(A ∑-=-1111n i i X n )(B ∑=-n i i X n 111 )(C ∑=n i i X n 21 )(D ∑-=111n i i X n 5、设4321,,,X X X X 是总体2(0,)N σ的样本,2σ未知,则下列随机变量是统计量的是(B ).(A )3/X σ; (B )414ii X=∑; (C )σ-1X ; (D )4221/ii Xσ=∑6、设总体),(~2σμN X ,1,,n X X L 为样本,S X ,分别为样本均值和标准差,则下列正确的是( C ).2() ~(,)A X N μσ 2() ~(,)B n X N μσ 22211()()~()ni i C X n μχσ=-∑)() ~()X D t n Sμ-7、设总体X 服从两点分布B (1,p ),其中p 是未知参数,15,,X X ⋅⋅⋅是来自总体的简单随机样本,则下列随机变量不是统计量为( C )( A ) . 12X X +( B ){}max ,15i X i ≤≤( C ) 52X p +( D ) ()251X X -8、设1,,n X X ⋅⋅⋅为来自正态总体2(,)N μσ的一个样本,μ,2σ未知。
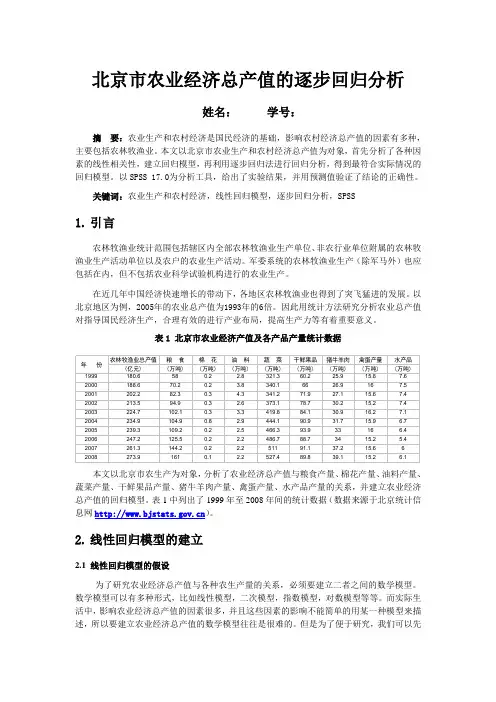
北京市农业经济总产值的逐步回归分析姓名:学号:摘要:农业生产和农村经济是国民经济的基础,影响农村经济总产值的因素有多种,主要包括农林牧渔业。
本文以北京市农业生产和农村经济总产值为对象,首先分析了各种因素的线性相关性,建立回归模型,再利用逐步回归法进行回归分析,得到最符合实际情况的回归模型。
以SPSS 17.0为分析工具,给出了实验结果,并用预测值验证了结论的正确性。
关键词:农业生产和农村经济,线性回归模型,逐步回归分析,SPSS1.引言农林牧渔业统计范围包括辖区内全部农林牧渔业生产单位、非农行业单位附属的农林牧渔业生产活动单位以及农户的农业生产活动。
军委系统的农林牧渔业生产(除军马外)也应包括在内,但不包括农业科学试验机构进行的农业生产。
在近几年中国经济快速增长的带动下,各地区农林牧渔业也得到了突飞猛进的发展。
以北京地区为例,2005年的农业总产值为1993年的6倍。
因此用统计方法研究分析农业总产值对指导国民经济生产,合理有效的进行产业布局,提高生产力等有着重要意义。
表1 北京市农业经济产值及各产品产量统计数据本文以北京市农生产为对象,分析了农业经济总产值与粮食产量、棉花产量、油料产量、蔬菜产量、干鲜果品产量、猪牛羊肉产量、禽蛋产量、水产品产量的关系,并建立农业经济总产值的回归模型。
表1中列出了1999年至2008年间的统计数据(数据来源于北京统计信息网)。
2.线性回归模型的建立2.1 线性回归模型的假设为了研究农业经济总产值与各种农生产量的关系,必须要建立二者之间的数学模型。
数学模型可以有多种形式,比如线性模型,二次模型,指数模型,对数模型等等。
而实际生活中,影响农业经济总产值的因素很多,并且这些因素的影响不能简单的用某一种模型来描述,所以要建立农业经济总产值的数学模型往往是很难的。
但是为了便于研究,我们可以先假定一些前提条件,然后在这些条件下得到简化后的近似模型。
以下我们假定两个前提条件:1) 农产品的价格是不变的。

1、设总体服从泊松分布P (λ),1,,n X X L 是一样本:(1)写出1,,n X X L 的概率分布;(2)计算2,n EX DX ES 和;(3)设总体容量为10的一组样本观察值为(1,2,4,3,3,4,5,6,4,8)试计算样本均值, 样本方差和次序统计量的观察值。
解:由于),,2,1(/1,/12n i DX EX i i ===λλ,所以(2)λ1)(1)1(11===∑∑==n i i n i i X E n X n E X E ; 21211)(1)1(λn X D nX n D X D n i i n i i ===∑∑==; 221212)1(111)(11])(11[λλ-=⋅-=-=--=∑∑==n n n n X D n X X n E ES n i i n i i (3)2、设总体X 服从()0,1N ,样本16,,X X L 来自总体X, 令()()22123456Y X X X X X X =+++++, 求常数C ,使CY 服从2χ-分布。
解:因为样本独立同分布,所以服从,服从,同理服从, 因此服从,服从,且两者相互独立,由-分布的可加性,知Y/3服从,所以取C=1/3 。
3、已知随机变量X 服从t 分布,自由度为n ,证明随机变量F= 2X 服从F 分布,自由度为(1,n )。
证明:因为X~t(k),由定义可令X=A/根号下B/k ,其中A~N(0,1),B~X^2(k)分布Y=X^2=A^2/(B/k),因为A~N(0,1),所以A^2~X^2(k)Y=(A^2/1)/(B/K),则由定义可知Y~F(1,k)4、设总体X 服从()2,N μσ,X 和2S 为样本均值和样本修正方差,又有1n X +服从()2,N μσ,且与1,,n X X L()212 /1n X X Xn S n +-+服从什么分布。
解:由X 服从2,N n σμ⎛⎫ ⎪⎝⎭,1n X +服从()2,N μσ,1n X X +-服从210,n N n σ+⎛⎫ ⎪⎝⎭,X 服从()0,1N ,又由22n nS σ服从自由度为n-1的2χ-分布,由定理1.3.6知X 与22n nS σ相互独立,而1n X +与1,,n X X LX 与22n nS σ相互独立。

自然语言中困惑度问题的统计分析姓名:李楠学号:20120102015专业方向:计算机应用技术2012年11月2日摘要数理统计学是研究随机现象统计规律性的一门数学学科,它以概率论为基础,研究如何收集、整理和分析带有误差的随机数据,建立适当的随机数学模型,并在此基础上对随机现象的本质规律性给出推断和预测,为决策提供科学依据。
本文依据数理统计学的知识,通过测试一百多篇语料的困惑度,得出110个样本数据,通过对困惑度样本数据加工处理和汇总后,给出矩估计和极大似然估计、给出参数估计区间、给出参数的t检验和2 检验,进行非参数拟合优度检验,从而得出相应的结论,即判断一个语言模型的好坏。
关键词:困惑度;数理统计;参数估计;假设检验目录前言 ............................................................... 3 一、采集样本及数据整理 (4)1、数据的搜集方法及说明2、数据整理:给出频数、频率分布表及说明3、画出直方图和折线图并给出说明4、画出经验分布函数二、假定总体服从正态分布,给出μ,2σ的估计 (10)1、矩估计法2、极大似然估计3、若总体不是正态分布请探求其参数估计,并写出方案三、参数区间估计 (12)1、方差2σ未知,求数学期望μ的置信区间 ......................... 12 2、数学期望μ,2σ均未知,求方差2σ的置信区间 . (13)注:可先假设总体是正态时进行讨论,若总体不是正态的要给出探求方案四、 参数的假设检验 (14)1. 样本统计数据的t 检验 ....................................... 14 2. 样本统计数据的-2χ检验 .................................................................................... 15 五、非参数假设检验(2χ拟合优度检验或K —S 检验) . (17)1、2χ拟合优度检验或K —S 检验检验2、当上述检验被接受或被拒绝时,请结合实际问题给出说明六、结论 .......................................................... 20 总结、评述和体会参考文献 (21)前言自然语言处理是一项十分庞大而繁复的工程,它是自然科学和社会科学交叉的学科。

西南大学2016年春《数理统计》作业及答案(已整理)第一次作业1、设总体X 服从正态分布),(2σμN ,其中μ已知,2σ未知,n X X X ,,,21 为其样本,2≥n ,则下列说法中正确的是( )。
(A )∑=-ni iXn122)(μσ是统计量 (B )∑=ni i X n122σ是统计量 (C )∑=--ni iXn 122)(1μσ是统计量 (D )∑=ni iX n12μ是统计量2、设两独立随机变量)1,0(~N X ,)9(~2χY ,则YX 3服从( )。
3、设两独立随机变量)1,0(~N X ,2~(16)Y χ服从( )。
4、设n X X ,,1 是来自总体X 的样本,且μ=EX ,则下列是μ的无偏估计的是( ).5、设4321,,,X X X X 是总体2(0,)N σ的样本,2σ未知,则下列随机变量是统计量的是( ).(A )3/X σ; (B )414ii X=∑; (C )σ-1X ; (D )4221/ii Xσ=∑6、设总体),(~2σμN X ,1,,n X X L 为样本,S X ,分别为样本均值和标准差,则下列正确的是( ).7、设总体X 服从两点分布B (1,p ),其中p 是未知参数,15,,X X ⋅⋅⋅是来自总体的简单随机样本,则下列随机变量不是统计量为( )( A ) . 12X X +( B ){}max ,15i X i ≤≤( C ) 52X p +( D )()251X X -8、设1,,n X X ⋅⋅⋅为来自正态总体2(,)N μσ的一个样本,μ,2σ未知。
则2σ的最大似然估计量为( )。
(A )∑=-n i i X n 12)(1μ (B )()211∑=-n i i X X n (C )∑=--n i i X n 12)(11μ(D )()∑=--n i iX X n 1211 答案:1、(D );2、 )(C ;3、)(C ;4、)(A ;5、(B );6、() ;C 7、( C ) ;8、(B )。
研究生课程考核试卷科目:数理统计教师: 李寒宇姓名: 蔡亚楠学号:20131102015t 专业:高电压与绝缘技术类别:学术型上课时间: 2014年3月至2014年5月考生成绩:卷面成绩平时成绩课程综合成绩阅卷评语:阅卷教师(签名)相对地过电压数据的统计分析摘要:过电压是指超过正常运行电压并可使电力系统绝缘或保护设备损坏的电压升高。
电力系统的过电压分布情况决定了电气设备的绝缘水平。
变电站过电压由于影响因素的随机性,使得过电压数据复杂且具有随机性。
本文结合电气工程专业的背景,分析了相对地过电压数据的分布规律。
首先对三相的过电压数据分别进行双样本同分布检验,采用两总体分布比较的假设检验方法。
检验结果显示三相的样本具有相同的分布规律,因此将三相的过电压数据合并进行总体的分布规律检验。
文中运用拟合优度2 检验法检验总体分布是否福才能够正态分布。
检验结果表明样本总体分布不服从正态分布,而是服从切断正态分布.针对相对地过电压数据的统计分析有助于确定设备的绝缘水平,具有一定的研究价值.关键词:过电压;假设检验;统计分布一、问题提出过电压是指超过正常运行电压并可使电力系统绝缘或保护设备损坏的电压升高。
电力系统的过电压分布情况决定了电气设备的绝缘水平.由于过电压数据出现的随机性较大,且有明显的统计特征,因此在对单次过电压数据进行统计分析的同时,还可以用数理统计的方法对系统采集的多次样本进行统计分析研究,并预测过电压的概率分布规律,以便将所得结论用于确定设备及线路的绝缘水平,合理解决绝缘配合问题,使设备绝缘故障率或停电故障率降低到经济上和安全运行上可以接受的水平.二、数据描述本次研究以TR2000过电压在线监测装置在某变电站实地运行所采集的过电压数据进行分析。
该变电站的等级为110kV/38.5kV/10。
5kV,以往的运行经验发现,35kV侧事故频繁,属第一、二类等级符合用户较集中,故在35kV侧安装了一台TR2000过电压在线监测装置.通过对监测装置中导出的数据进行进制转换、图形显示、统计分析等手段,分析变电战过电压的规律,由此可以对电力系统设计、改造和故障分析等工作提供可靠的依据.根据现场情况,将暂态过电压记录倍率设定为1。
沈阳铁路局学习中心第一部分:必须掌握的重点理论知识习题。
一、 填空:1、设{1,2,3,4,5,6}Ω=,{2,3,4}A =,{3,5}B =,{4,6}C =,那么A B ⋃= {1,2,3,4,6} ,AB = {1,6} ,()A BC = Φ空集 。
2、设随机变量X 与Y 相互独立,X 服从二项分布(5,0.6)B ,Y 服从二项分布2(,)N μσ,且()6,() 1.36E X Y D X Y +=-=,则μ=6-5=1 ;σ=根号0.76。
3则α= (1-0.2-0.1-0.25-0.15) 0.3 ,X 的期望()E x = (XP )0.1 4、离散型随机变量ξ的分布律为P(ξ=k)=2,1,2,3ck k=,则c= 36/49 c(1+1/4+1/9)=1,解得c; 5、从总体X 中抽取样本,得到5个样本值为5、2、3、4、1。
则该总体平均数的矩估计值是___5____,总体方差的矩估计是___15/2____。
6、设两个事件A 、B 相互独立,()0.6P A =,()0.7P B =,则()P A B -= 0.18 ,()P A B -= 0.12 。
7、设随机变量X 服从正态分布(2,16)N -,则{02}P X ≤<= Φ(1)-Φ(0.5) ,{6}P X ≥-= Φ(1) ,{22}P x -≥= 1-Φ(1.5)+Φ(0.5) 。
8则()E x = 0.05 ,2()E x = 1.75 。
9、 离散型随机变量ξ的分布律为P(ξ=k)=.3,2,1,2=k kc,则c= 12/11 10、甲、乙两人独立的对同一目标射击一次,其命中率分别为0.6,0.5。
现已知目标被命中,则它是甲射中的概率为0.75。
11、设随机事件,A B 及其和事件A B ⋃的概率分别为0.4,0.3和0.6。
若B 表示B 的对立事件,那说明: ①阶段测试作业必须由学生书写完成,打印复印不计成绩。
F 列正确的是( )(A) X ~ N(4®2) (B) ∏X ~ N(* )(C)W(X i 」)2 〜2(n)(D)竺 )〜t(n)σ2GS7、设总体X 服从两点分布B (i, P),其中P 是未知参数,X i ,…,X 5是来自总体的简单随 机样本,则下列随机变量不是统计量为()(A ) . X i X 2( B ) maχfχi ,仁i 岂51数理统计第一次1设总体X 服从正态分布N(J,;「2),其中J已知,;「2未知, X 1,X 2,…,X n 为其样本, n _ 2,则下列说法中正确的是( )。
(A ) ∙ (X j -■•二)2 是统计量 n i 1 (B)=J Xj2是统计量 n i =I2、设两独立随机变量 X ~ N(O,i), Y~ 2(9),则 3X服从( JY)0(A) N(0,i) (B)t(3) (C)t(9) (D) F(i,9) 3、设两独立随机变量 X 〜N(O,i),24X Y~ 2(i6),则-服从( )0 (A)N(O,i) (B)t ⑷(C)t(i6)(D) F(i,4)(C)=J (X i 一)2是统计量n —1 y (D ) X i 2是统计量 n i =I4、设X i ,…,X n 是来自总体X 的样本,且EX 二,则下列是」的无偏估计的是()I n-Ii ni n(A) X i (B) 一 X i (C)-^ X in — 1 i =I n —1iτn^(D)-XX in5、设X i ,X 2,X 3,X 4是总体N(0M 2)的样本,2-未知,则下列随机变量是统计量的是( ). (A) X 3/二;(B )4(Di Xi 2 / ~2i T26、设总体X ~ Ne I ^ ) , X i ,L ,X n 为样本,X,S 分别为样本均值和标准差,则1、( D );2、(C) ; 3、(C) ; 4、(A) ;5、( B );6、(C) ; 7、( C );第二次1、设总体X~N(*二2),X 1, ,X n 为样本,X,S 分别为样本均值和标准差)分布•3、在假设检验中,下列说法正确的是(如果原假设是正确的,但作出的决策是接受备择假设,则犯了第一类错误; 如果备择假设是正确的,但作出的决策是拒绝备择假设,则犯了第一类错误; 第一类错误和第二类错误同时都要犯;如果原假设是错误的,但作出的决策是接受备择假设,则犯了第二类错误。
应用数理统计作业一学号:姓名:电话:二〇一四年十二月国内生产总值的多元线性回归模型摘要:本文首先选取了选取我国自1978至2012年间的国内生产总值为因变量,并选取了7个主要影响因素,进一步利用统计软件SPSS对以上数据进行了多元逐步线性回归。
从而找到了能反映国内生产总值与各因素之间关系的“最优”回归方程.然后利用多重线性的诊断找出存在共线性的自变量,剔除缺失值较多的因子.再次进行主成份线性回归分析,找出最优回归方程。
所得结论与我国当前形势相印证。
关键词:多元线性回归,逐步回归法,多重共线性诊断,主成份分析目录0符号说明 (1)1 介绍 (2)2 统计分析步骤 (3)2。
1 数据的采集和整理 (3)2。
2采用多重逐步回归分析 (7)2.3进行共线性诊断 (17)2。
4进行主成分分析确定所需主成份 (24)2。
5进行主成分逐步回归分析 (27)3 结论 (30)参考文献 (31)致谢 (32)0符号说明1 介绍文中主要应用逐步回归的主成份分析方法,对数据进行分析处理,最终得出能够反映各个因素对国内生产总值影响的最“优”模型及线性回归方程.国内生产总值是指在一定时期内(一个季度或一年),一个国家或地区的经济中所生产出的全部最终产品和劳务的价值,常被公认为衡量国家经济状况的最佳指标.它不但可反映一个国家的经济表现,还可以反映一国的国力与财富。
2012年1月,国家统计局公布2011年重要经济数据,其中GDP增长9.2%,基本符合预期。
2012年10月18日,统计显示,2012年前三季度国内生产总值353480亿元,同比增长7.7%;其中,一季度增长8.1%,二季度增长7。
6%,三季度增长7.4%,三季度增幅创下2009年二季度以来14个季度新低。
中国的GDP核算历史不长,上世纪90年代之前通常用“社会总产值”来衡量经济发展情况。
上世纪80年代初中国开始研究联合国国民经济核算体系的国内生产总值(GDP)指标。
沈阳铁路局学习中心第一部分:必须掌握的重点理论知识习题。
一、 填空:1、设{1,2,3,4,5,6}Ω=,{2,3,4}A =,{3,5}B =,{4,6}C =,那么A B ⋃= {1,2,3,4,6} ,AB = {1,6} ,()A BC = Φ空集 。
2、设随机变量X 与Y 相互独立,X 服从二项分布(5,0.6)B ,Y 服从二项分布2(,)N μσ,且()6,() 1.36E X Y D X Y +=-=,则μ=6-5=1 ;σ=根号0.76。
3则α= (1-0.2-0.1-0.25-0.15) 0.3 ,X 的期望()E x = (XP )0.1 4、离散型随机变量ξ的分布律为P(ξ=k)=2,1,2,3ck k=,则c= 36/49 c(1+1/4+1/9)=1,解得c; 5、从总体X 中抽取样本,得到5个样本值为5、2、3、4、1。
则该总体平均数的矩估计值是___5____,总体方差的矩估计是___15/2____。
6、设两个事件A 、B 相互独立,()0.6P A =,()0.7P B =,则()P A B -= 0.18 ,()P A B -= 0.12 。
7、设随机变量X 服从正态分布(2,16)N -,则{02}P X ≤<= Φ(1)-Φ(0.5) ,{6}P X ≥-= Φ(1) ,{22}P x -≥= 1-Φ(1.5)+Φ(0.5) 。
8则()E x = 0.05 ,2()E x = 1.75 。
9、 离散型随机变量ξ的分布律为P(ξ=k)=.3,2,1,2=k kc,则c= 12/11 10、甲、乙两人独立的对同一目标射击一次,其命中率分别为0.6,0.5。
现已知目标被命中,则它是甲射中的概率为0.75。
11、设随机事件,A B 及其和事件A B ⋃的概率分别为0.4,0.3和0.6。
若B 表示B 的对立事件,那说明: ①阶段测试作业必须由学生书写完成,打印复印不计成绩。