习题课：人造地球卫星的轨道及变轨

2025届高考物理复习：经典好题专项（卫星的变轨和对接问题）练习1．我国2021年4月29日在海南文昌航天发射场用长征五号B遥二运载火箭成功将空间站“天和”核心舱送入预定圆轨道，中国空间站在轨组装建造全面展开。

关于火箭发射以及空间站的组合、对接，下列说法正确的是()A．火箭发射升空过程中，发动机喷出的燃气推动空气，空气推动火箭上升B．空间站在轨运行的速率可能大于7.9 km/sC．飞船要和在轨的核心舱对接，通常是将飞船发射到较低的轨道上，然后使飞船加速实现对接D．在空间站中工作的航天员因为不受地球引力作用，所以处于完全失重状态2. 如图所示，虚线Ⅰ、Ⅱ、Ⅲ分别表示地球卫星的三条轨道，其中轨道Ⅰ为与第一宇宙速度7.9 km/s对应的近地环绕圆轨道，轨道Ⅱ为椭圆轨道，轨道Ⅲ为与第二宇宙速度11.2 km/s对应的脱离轨道，a、b、c三点分别位于三条轨道上，b点为轨道Ⅱ的远地点，b、c点与地心的距离均为轨道Ⅰ半径的2倍，则()A．卫星在轨道Ⅱ的运行周期为轨道Ⅰ周期的2倍B．卫星经过a点的速率为经过b点速率的2倍C．卫星在a点的加速度大小为在c点加速度大小的2倍D．质量相同的卫星在b点的机械能小于在c点的机械能3. (2023ꞏ广东省模拟)如图所示，我国“天问一号”火星探测器先由地火转移轨道1进入火星停泊轨道2，进行相关探测后进入较低的轨道3开展科学探测，则探测器()A．在轨道2上近火点加速可进入轨道3B．在轨道2上近火点的机械能比远火点小C．在轨道1上的运行速度不超过第二宇宙速度D．在轨道2与轨道3同一近火点的加速度相等4. (多选)(2023ꞏ江西省第一次联考)我国的“天问一号”火星探测器被火星捕获后，经过多次调整，进入预设的环火圆轨道Ⅰ做匀速圆周运动，如图所示，椭圆轨道Ⅱ、Ⅲ为两次调整轨道，点A是两椭圆轨道的近火点，点B、C分别是椭圆轨道Ⅱ、Ⅲ的远火点，下列说法正确的是()A．“天问一号”在轨道Ⅱ上A点的速率大于在轨道Ⅰ上A点的速率B．“天问一号”在轨道Ⅱ上运行的周期小于在轨道Ⅲ上运行的周期C．“天问一号”在轨道Ⅰ上经过A点时的加速度大于在轨道Ⅱ上经过A点时的加速度D．“天问一号”在轨道Ⅱ上由A点运行到B点的过程中，万有引力对其做正功5．(多选)长征五号遥四运载火箭直接将我国首次执行火星探测任务的“天问一号”探测器送入地火转移轨道，自此“天问一号”开启了奔向火星的旅程。

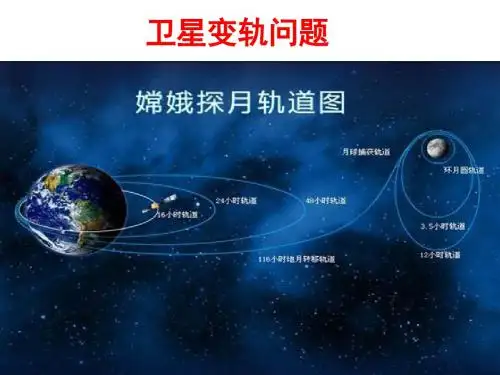
变轨问题专题练习一1、（05江苏）某人造卫星运动的轨道可近似看作是以地心为中心的圆．由于阻力作用，人造卫星到地心的距离从r1慢慢变到r2，用EKl．EK2分别表示卫星在这两个轨道上的动能，则A、r1<r2，EK1<EK2B、r1>r2，EK1<EK2C、r1<r2，EK1>EK2D、r1>r2，EK1>EK22、发射地球同步卫星时，先将卫星发射到近地圆轨道1，然后点火，使其沿椭圆轨道2运行，最后再次点火，将卫星送人同步圆轨道3。

轨道1、2相切于Q点，轨道2、3相切于P点，如图所示，，则当卫星分别在1、2、3轨道上正常运行时，下列说法中正确的是A．卫星在轨道3上的速率大于在轨道1上的速率B．卫星在轨道3上的角速度小于在轨道1上的角速度C．卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度D．卫星在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度3、我国成功实施了“神舟”七号载入航天飞行并实现了航天员首次出舱。

飞船先沿椭圆轨道飞行，后在远地点343千米处点火加速，由椭圆轨道变成高度为343千米的圆轨道，在此圆轨道上飞船运行周期约为90分钟。

下列判断正确的是( )A．飞船变轨前后的速度相等B．飞船在圆轨道上时航天员出舱前后都处于超重状态C．飞船在此圆轨道上运动的角速度大于同步卫星运动的角速度D．飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度4、我国“嫦娥一号”探月卫星发射后，先在“24小时轨道”上绕地球运行（即绕地球一圈需要24小时)；然后，经过两次变轨依次到达“48小时轨道”和“72小时轨道”；最后奔向月球。

如果按圆形轨道计算，并忽略卫星质量的变化，则在每次变轨完成后与变轨前相比，A．卫星速度增大，角速度减小 B．卫星速度增大，角速度增大C．卫星速度减小，角速度增加 D．卫星速度减小，角速度减小5、宇宙飞船和空间站在同一轨道上运动，若飞船想与前面的空间站对接，飞船为了追上轨道空间站，可采取的方法是( )A. 飞船加速直到追上空间站，完成对接B. 飞船从原轨道减速至一个较低轨道，再加速追上空间站完成对接C. 飞船加速至一个较高轨道再减速追上空间站完成对接D. 无论飞船采取何种措施，均不能与空间站对接航天飞月空间站 B 6、人造地球卫星在轨道半径较小的轨道A 上运行时机械能为E A ，它若进入轨道半径较大的轨道B 运行时机械能为E B ，在轨道变化后这颗卫星( ) A.动能减小，势能增加，E B ＞E A B.动能减小，势能增加，E B =E AC.动能减小，势能增加，E B ＜E AD.动能增加，势能增加，E B ＞E A7、发射地球同步卫星时，先将卫星发射至近地圆轨道1，然后经点火，使其沿椭圆轨道运行，最后再次点火将卫星送入同步圆轨道3，轨道1、2相切于Q 点，轨道2、3相切于P 点，如图所示，则卫星分别在轨道1、2、3上正常运行时，下列说法正确的是( )A.卫星在轨道3上的速率大于在轨道1上的速率B.卫星在轨道3上角速度的小于在轨道1上的角速度C.卫星在轨道1上经过Q 点时的加速度等于它在轨道2上经过Q点时的加速度D.卫星在轨道2上经过P 点时的加速度小于它在轨道3上经过P点时的加速度8、地球绕太阳的运动可视为匀速圆周运动,太阳对地球的万有引力提供地球绕太阳做圆周运动所需要的向心力,由于太阳内部的核反应而使太阳发光,在这个过程中,太阳的质量在不断减小.根据这一事实可以推知,在若干年后,地球绕太阳的运动情况与现在相比( ) A.运动半径变大 B.运动周期变大 C.运动速率变大 D.运动角速度变大9、我国未来将建立月球基地，并在绕月轨道上建造空间站．如图所示，关闭动力的航天飞机在月球引力作用下经椭圆轨道向月球靠近，并将与空间站在B 处对接.已知空间站绕月轨道半径为r ，周期为T ，万有引力常量为G ，下列说法中正确的是（ ）A ．图中航天飞机在飞向B 处的过程中，月球引力做正功 B ．航天飞机在B 处由椭圆轨道可直接进入空间一站轨道C ．根据题中条件可以算出月球质量D ．根据题中条件可以算出空间站受到月球引力的大小10、 在“嫦娥一号”奔月飞行过程中,在月球上空有一次变轨是由椭圆轨道a 变为近月圆形轨道b,如图所示.在a 、b 切点处,下列说法正确的是( ) A.卫星运行的速度v a = v b B.卫星受月球的引力F a = F b C.卫星的加速度 a a > a b D.卫星的动能E ka < E kb21 3P Q参考答案：1、B 2、BD 3、C 4、D 5、B 6、A 7、BC 8、AB 9、AC 10、B。

教学研究新课程NEW CURRICULUM天体的运行问题是高考的热点问题，在椭圆轨道和变轨问题上，中学阶段基本上都是做定性解释，很少做定量计算，且在教学实践中，一些学习优秀、善于思考的学生往往会在此类问题上提出更深层次的问题，如卫星在椭圆轨道的近、远地点的向心加速度大小和不同轨道的向心加速度、速度大小怎么比较？在用F n =m v 2r、a n =v 2r求解时，在近、远地点的“r ”到底是哪个量？怎么求？虽然学生提出的问题有的已经超出中学生应当掌握的范围，但是从激励学生的探究需求出发，对一些优秀的学生在这些问题上可适当做些拓展，况且作为授业解惑的教师，也需要对这些问题有个清楚的认识。

可是在教学实践中发现一些教师由于在这些问题上认识不清甚至根本不知道，经常被学生问得手足无措而避而不谈或者作出错误解释，一些材料在这些问题上的解释往往也是模棱两可。

若想对椭圆轨道的有关问题进行定量计算，首先必须对椭圆的曲率和曲率半径等有关知识有清晰的认识。

一、椭圆的曲率半径1.曲线的曲率和曲率半径曲率是描述曲线弯曲的程度，曲线y =f （x ）（设x =Φ（t ），y =φ（t ））的曲率的计算公式为k =x ′y ″-x ″y ′x ′2+y ′2[]32。

如图1所示，设k （k ≠0）为曲线y=f （x ）在点M 处的曲率，圆C 与曲线相切于M 点，若CM=R =1k ，圆C 称为曲线在点M 的曲率圆，圆C 的半径R 则称为曲线在点M 的曲率半径。

故曲率半径的计算公式为：R =1k =x ′2+y ′2[]32x ′y ″-x ″y ′—————①（1）2.椭圆的曲率半径如图2，a 是椭圆的半长轴，b 是椭圆的半短轴，椭圆的参数方程为：x=a cos θ，y=a sin θ。

把x ′=-a sin θ、x ″=-a cos θ、y ′=b cos θ、y ″=-b sin θ代入①式得：R =（a 2sin 2θ+b 2cos 2θ）32ab，取不同的θ值可以求得椭圆不同位置的曲率半径，比如把P （θ=0）和Q （θ=π）代入椭圆曲率半径公式可得：P 、Q 两点的曲率半径均为b 2a，A 、B 两点的曲率半径均为a 2b 。

人造卫星变轨问题专题一、人造卫星基本原理绕地球做匀速圆周运动的人造卫星所需向心力由万有引力提供。

轨道半径r 确定后，与之对GM、周期T 2r 3、向心加速度 a GM应的卫星线速度 v 也都是确定的。

如果卫星r 2rGM的质量也确定，一旦卫星发生变轨，即轨道半径r 发生变化，上述物理量都将随之变化。

同理，只要上述物理量之一发生变化，另外几个也必将随之变化。

在高中物理中，会涉及到人造卫星的两种变轨问题。

二、渐变由于某个因素的影响使卫星的轨道半径发生缓慢的变化（逐渐增大或逐渐减小） ，由于半径变化缓慢，卫星每一周的运动仍可以看做是匀速圆周运动。

解决此类问题，首先要判断这种变轨是离心还是向心，即轨道半径是增大还是减小，然后再判断卫星的其他相关物理量如何变化。

如：人造卫星绕地球做匀速圆周运动，无论轨道多高，都会受到稀薄大气的阻力作用。

如果不及时进行轨道维持（即通过启动星上小型火箭，将化学能转化为机械能，保持卫星应具有的速度），卫星就会自动变轨，偏离原来的圆周轨道，从而引起各个物理量的变化。

由于这种变轨的起因是阻力，阻力对卫星做负功， 使卫星速度减小， 所需要的向心力m v 2减r小了，而万有引力大小GMm没有变，因此卫星将做向心运动，即半径r 将减小。

r 2由㈠中结论可知：卫星线速度 v 将增大，周期 T 将减小，向心加速度三、突变由于技术上的需要，有时要在适当的位置短时间启动飞行器上的发动机，使飞行器轨道发生突变，使其到达预定的目标。

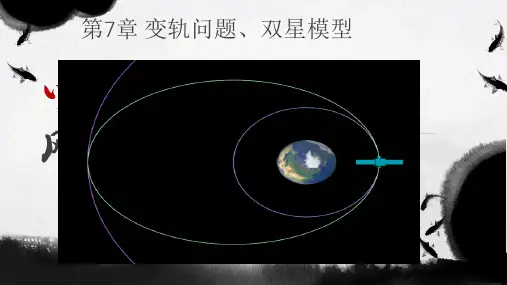
如：发射同步卫星时，通常先将卫星发送到近地轨道Ⅰ，使其绕地球做匀速圆周运动，速率为v 1，第一次在 P 点点火加速，在短时间内将速率由 v 1 增加到 v 2，使卫星进入椭圆形的转移轨道Ⅱ；卫星运行到远地点 Q 时的速率为 v 3，此时进行第二次点火加速， 在短时间内将速率由 v 3 增加到 v 4，使卫星进入同步轨道Ⅲ， 绕地球做匀速圆周运动。

a 将增大。

v 3ⅢQ v 4v 1 Ⅱ Ⅰ Pv 2第一次加速：卫星需要的向心力mv 2 增大了，但万有引力 GMm 没变，因此卫星将开始做rr 2离心运动，进入椭圆形的转移轨道Ⅱ。

人造卫星变轨及错题解析一、人造卫星基本原理绕地球做匀速圆周运动的人造卫星所需向心力由万有引力提供。

轨道半径r 确定后，与之对应的卫星线速度r GM v =、周期GMr T 32π=、向心加速度2r GM a =也都是确定的。

如果卫星的质量也确定，一旦卫星发生变轨，即轨道半径r 发生变化，上述物理量都将随之变化。

同理，只要上述物理量之一发生变化，另外几个也必将随之变化。

在高中物理中，会涉及到人造卫星的两种变轨问题。

二、渐变由于某个因素的影响使卫星的轨道半径发生缓慢的变化（逐渐增大或逐渐减小），由于半径变化缓慢，卫星每一周的运动仍可以看做是匀速圆周运动。

解决此类问题，首先要判断这种变轨是离心还是向心，即轨道半径是增大还是减小，然后再判断卫星的其他相关物理量如何变化。

如：人造卫星绕地球做匀速圆周运动，无论轨道多高，都会受到稀薄大气的阻力作用。

如果不及时进行轨道维持（即通过启动星上小型火箭，将化学能转化为机械能，保持卫星应具有的速度），卫星就会自动变轨，偏离原来的圆周轨道，从而引起各个物理量的变化。

由于这种变轨的起因是阻力，阻力对卫星做负功，使卫星速度减小，所需要的向心力rmv 2减小了，而万有引力大小2r GMm 没有变，因此卫星将做向心运动，即半径r 将减小。

由㈠中结论可知：卫星线速度v 将增大，周期T 将减小，向心加速度a 将增大。

三、突变 由于技术上的需要，有时要在适当的位置短时间启动飞行器上的发动机，使飞行器轨道发生突变，使其到达预定的目标。

如：发射同步卫星时，通常先将卫星发送到近地轨道Ⅰ，使其绕地球做匀速圆周运动，速率为v 1，第一次在P 点点火加速，在短时间内将速率由v 1增加到v 2，使卫星进入椭圆形的转移轨道Ⅱ；卫星运行到远地点Q 时的速率为v 3，此时进行第二次点火加速，在短时间内将速率由v 3增加到v 4，使卫星进入同步轨道Ⅲ，绕地球做匀速圆周运动。

第一次加速：卫星需要的向心力r mv 2增大了，但万有引力2rGMm 没变，因此卫星将开始做离心运动，进入椭圆形的转移轨道Ⅱ。

人造卫星变轨问题一、人造卫星基本原理绕地球做匀速圆周运动的人造卫星所需向心力由万有引力提供。

轨道半径r 确定后，与之对应的卫星线速度r GM v =、周期GMr T 32π=、向心加速度2r GM a =也都是确定的。

如果卫星的质量也确定，一旦卫星发生变轨，即轨道半径r 发生变化，上述物理量都将随之变化。

同理，只要上述物理量之一发生变化，另外几个也必将随之变化。

在高中物理中，会涉及到人造卫星的两种变轨问题。

二、渐变由于某个因素的影响使卫星的轨道半径发生缓慢的变化（逐渐增大或逐渐减小），由于半径变化缓慢，卫星每一周的运动仍可以看做是匀速圆周运动。

解决此类问题，首先要判断这种变轨是离心还是向心，即轨道半径是增大还是减小，然后再判断卫星的其他相关物理量如何变化。

如：人造卫星绕地球做匀速圆周运动，无论轨道多高，都会受到稀薄大气的阻力作用。

如果不及时进行轨道维持（即通过启动星上小型火箭，将化学能转化为机械能，保持卫星应具有的速度），卫星就会自动变轨，偏离原来的圆周轨道，从而引起各个物理量的变化。

由于这种变轨的起因是阻力，阻力对卫星做负功，使卫星速度减小，所需要的向心力r mv 2减小了，而万有引力大小2r GMm 没有变，因此卫星将做向心运动，即半径r 将减小。

由㈠中结论可知：卫星线速度v 将增大，周期T 将减小，向心加速度a 将增大。

三、突变由于技术上的需要，有时要在适当的位置短时间启动飞行器上的发动机，使飞行器轨道发生突变，使其到达预定的目标。

如：发射同步卫星时，通常先将卫星发送到近地轨道Ⅰ，使其绕地球做匀速圆周运动，速率为v 1，第一次在P 点点火加速，在短时间内将速率由v 1增加到v 2，使卫星进入椭圆形的转移轨道Ⅱ；卫星运行到远地点Q 时的速率为v 3，此时进行第二次点火加速，在短时间内将速率由v 3增加到v 4，使卫星进入同步轨道Ⅲ，绕地球做匀速圆周运动。

第一次加速：卫星需要的向心力r mv 2增大了，但万有引力2rGMm 没变，因此卫星将开始做离心运动，进入椭圆形的转移轨道Ⅱ。