下载文档原格式
ANSYS电磁场分析指南（共17章）ANSYS电磁场分析指南第一章磁场分析概述：ANSYS电磁场分析指南第二章 2-D静态磁场分析：ANSYS电磁场分析指南第三章２-Ｄ谐波（ＡＣ）磁场分析：ANSYS电磁场分析指南第四章２-Ｄ瞬态磁场分析：ANSYS电磁场分析指南第五章３-Ｄ静态磁场分析（标量法）：ANSYS电磁场分析指南第六章３-Ｄ静态磁场分析（棱边元方法）：ANSYS电磁场分析指南第七章３-Ｄ谐波磁场分析（棱边单元法）：ANSYS电磁场分析指南第八章３-D瞬态磁场分析（棱边单元法）：ANSYS电磁场分析指南第九章 3-D静态、谐波和瞬态分析（节点法）：ANSYS电磁场分析指南第十章高频电磁场分析：ANSYS电磁场分析指南第十一章磁宏：ANSYS电磁场分析指南第十二章远场单元：ANSYS电磁场分析指南第十三章电场分析：ANSYS电磁场分析指南第十四章静电场分析（h方法）：ANSYS电磁场分析指南第十五章静电场分析（P方法）：ANSYS电磁场分析指南第十六章电路分析：ANSYS电磁场分析指南第十七章其它分析选项和求解方法：第一章磁场分析概述1.1磁场分析对象利用ANSYS/Emag或ANSYS/Multiphysics模块中的电磁场分析功能，ANSYS可分析计算下列的设备中的电磁场，如：·电力发电机·磁带及磁盘驱动器·变压器·波导·螺线管传动器·谐振腔·电动机·连接器·磁成像系统·天线辐射·图像显示设备传感器·滤波器·回旋加速器在一般电磁场分析中关心的典型的物理量为：·磁通密度·能量损耗·磁场强度·磁漏·磁力及磁矩· S-参数·阻抗·品质因子Q·电感·回波损耗·涡流·本征频率存在电流、永磁体和外加场都会激励起需要分析的磁场。
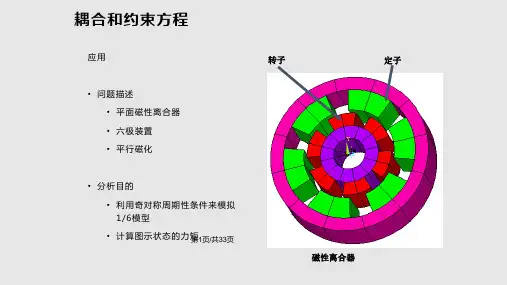
第四章２-Ｄ瞬态磁场分析什么是瞬态磁场分析瞬态磁场分析处置的既不是静态的也不是谐波的磁场，而是由电压、电流或外加场的随时刻无规律转变所引发的磁场转变。
在瞬态磁场分析中咱们所感爱好的典型物理量是：·涡流·涡流致使的磁力·涡流致使的能量损耗瞬态磁场分析能够是线性，也能够是非线性。
2-D瞬态磁场分析顶用到的单元在涡流区域，瞬态模型只能用矢量位方程描述。
只能用以下单元类型来模拟涡流区。
表12D实体单元表2通用电路单元创建2D瞬态磁场分析的物理环境犹如ANSYS其他类型分析一样，瞬态磁分析要成立物理环境、建模、给模型区域赋属性、划分网格、加边界条件和载荷、求解、然后检察结果。
2D瞬态磁分析的大多数步骤都相同或相似于2D静态磁场分析步骤。
本章讨论2D瞬态磁场分析中需要特殊处置的部份。
关于2D瞬态磁场分析中如何设置GUI参考框、单元选项（KEYOPTs）、实常数、单位制与2D静态磁场分析相同，第2章已经作了详细描述。
当概念材料性质时，一样也采纳与第2章中一样的方式。
成立模型，划分网格，指定属性《ANSYS建模与分网指南》详细介绍了建模进程。
成立了模型后，对每一个模型区要指定属性，即指定在第一步中概念好的单元类型、单元选项、材料特性、实常数、单元坐标系等。
利用AATT或VATT命令或其等效途径来指定属性。
详见第2章静态磁场分析部份。
施加边界条件和励磁载荷在瞬态磁分析中，可将边界条件和载荷施加到实体模型上（关键点、线和面），也能够施加到有限元模型上（节点和单元）。
加载方式与第2章静态分析类似。
也能够用命令加载和施加边界条件，对2D 瞬态分析还能够用加载步选项。
本手册第16章对这些载荷步选择有详细描述。
依照概念，瞬态分析中的边界条件和载荷是时刻的函数，实际分析计算时，要将“载荷－时刻”曲线分解成适合的载荷步，“载荷－时刻”曲线的每一个＂拐点＂确实是一个载荷步。
在每一个载荷步中，不仅要概念载荷或边界条件的值，而且还要概念它们所对应的时刻值和一些载荷步选项（如阶跃转变载荷或斜坡转变载荷、自动时刻步长等），重复将这些载荷数据写到载荷步文件中，直到所有的载荷步终止。
ANSYS软件对电机磁场的分析徐海峰辛慧源(浙江大学，浙江杭州 310027)摘要：本文重点介绍了用ANSYS软件分析电机磁场，使ANSYS软件具有"计算和分析"电机磁场的功能，从而进行电机的优化设计。
关键词： ANSYS；电机磁场；优化设计中图分类号：TP21 文献标识码：A1 前言磁路设计是电机设计的主要部分，磁路量对电机的主要性能起决定性的影响，电机的转矩和反电势直接取决于主磁通量。
因此磁路法是工程上最适用的电机计算方法。
所以从根本上讲，电机问题是一个电磁场的问题，由于永磁材料的引入，使许多传统的分析方法感到力不从心，所以对无刷直流电机进行磁场的研究还是非常必要的。
ANSYS软件是世界上著名的大型通用有限元计算软件，具有强大的求解器和前、后处理功能，为我们解决复杂、庞大的工程项目和致力于高水平的科研攻关提供了一个有两地工作环境，更使我们从繁琐、单调的常规有限元编程中解脱出来。
2ANSYS分析电机磁场的基本原理工程上的磁场分析一般采用数值计算方法。
常见的数值计算方法有有限差分法和有限元法。
差分法不适合于边界条件复杂、边界不规则(外部或内部)的情况。
为了充分发挥永磁材料的磁性能。
特别是稀土永磁的优导磁性能，用很少的永磁材料和加工费用制造出高性能的永磁电机，就不能简单套用传统的结构和设计计算方法。
必须应用现代设计思想，研究新的分析计算方法，以提高设计计算的准确度。
为此，本文采用有限元分析法。
使用有限元分析，目前一般有三种作法：a)用数学关系式建模，用计算机算法语言编制了网格自动剖分程序、有限元分析程序、相关的前后处理程序、电磁计算程序；这是传统的有限元分析方法。
b)采用有限元分析软件对电机内的电磁场进行简单的分析计算，完成电机设计中的磁路部分的设计，利用MATLAB等类似软件编制了电磁计算等其他设计程序。
c)大量工作均用高级的有限元分析软件完成，诸如力矩、电感、磁力线、磁通、磁场强度均一次性得出，使设计真正成为一种优化设计，设计过程即为分析过程。
ANSYS电磁场分析指南磁宏磁宏分析是ANSYS中的一种电磁场分析方法，用于模拟磁场中的行为。
它基于麦克斯韦方程组和磁性材料的本质特性，可以用来研究磁场的分布、场强和磁通量等。
以下是使用ANSYS进行磁宏分析的一般步骤：1.创建几何模型：使用ANSYS的几何建模工具创建您要分析的几何体。
您可以使用ANSYS的二维或三维建模功能，根据您的需求选择适当的几何形状。
2.设置材料属性：在进行磁宏分析之前，您需要为模型中的材料定义磁性属性。
这包括磁导率、磁饱和和磁滞等。
可以通过库中的材料属性进行选择，或者根据实际材料的特性手动输入。
如果您使用的是标准材料，可以轻松从ANSYS材料库中选择。
3.设置边界条件：确定分析的边界条件非常重要。
根据您的应用场景，您可以设置边界条件为固定零磁场、非磁性条件或具有特定磁场分布的条件。
对于二维问题，您可以设置边界上的磁通量。
这些边界条件将在后续计算中起作用。
4.生成网格：ANSYS使用有限元方法进行分析，因此需要生成适当的网格。
您可以选择不同的网格生成技术，例如自动网格细化、手动加密和剖面网格。
网格的质量对分析结果的准确性和计算时间都有重要影响。
5.定义分析类型和求解器：在ANSYS中，您可以选择不同的分析类型和求解器来求解磁场问题。
例如，您可以选择求解静态磁场、谐振频率或非线性磁场等。
根据您的需求选择适当的求解器，以获得准确的结果。
6.运行计算：在设置了适当的材料属性、边界条件和网格后，您可以运行计算。
ANSYS将使用选择的求解器进行计算，并在计算结束后生成结果。
7.分析结果：计算完成后，您可以查看和分析生成的结果。
这包括磁场分布图、场强、感应电流和磁通量等。
ANSYS提供了丰富的后处理工具，可以帮助您更好地理解分析结果。
除了这些基本步骤，在进行磁宏分析时还有一些注意事项和技巧：1.材料特性选择：选择适当的磁性材料特性对分析结果至关重要。
根据实际材料数据进行选择，并注意磁导率的非线性特性。
第十一章磁宏11.1 什么是电磁宏电磁宏是ANSYS宏命令，其主要功能是帮助用户方便地建立分析模型、方便地获取想要观察的分析结果。
目前，ANSYS提供了下列宏命令，可用于电磁场分析：·CMATRIX：计算导体间自有和共有电容系数·CURR2D：计算二维导电体内电流·EMAGERR：计算在静电或电磁场分析中的相对误差·EMF：沿预定路径计算电动力（emf）或电压降·FLUXV：计算通过闭合回路的通量·FMAGBC：对一个单元组件加力边界条件·FMAGSUM：对单元组件进行电磁力求和计算·FOR2D：计算一个体上的磁力·HFSWEEP：在一个频率范围内对高频电磁波导进行时谐响应分析，并进行相应的后处理计算·HMAGSOLV：定义2-D谐波电磁求解选项并进行谐波求解·IMPD：计算同轴电磁设备在一个特定参考面上的阻抗·LMATRIX：计算任意一组导体间的电感矩阵·MAGSOLV：对静态分析定义磁分析选项并开始求解·MMF：沿一条路径计算磁动力·PERBC2D：对2—D平面分析施加周期性约束·PLF2D：生成等势的等值线图·PMGTRAN：对瞬态分析的电磁结果求和·POWERH：在导体内计算均方根（RMS）能量损失·QFACT：根据高频模态分析结果计算高频电磁谐振器件的品质因子·RACE：定义一个“跑道形”电流源·REFLCOEF：计算同轴电磁设备的电压反射系数、驻波比、和回波损失·SENERGY：计算单元中储存的磁能或共能·SPARM：计算同轴波导或TE10模式矩形波导两个端口间的反射参数·TORQ2D：计算在磁场中物体上的力矩·TORQC2D：基于一个圆形环路计算在磁场中物体上的力矩·TORQSUM：对2-D平面问题中单元部件上的Maxwell力矩和虚功力矩求和本章对这些宏有详细描述。
第十一章磁宏11.1 什么是电磁宏电磁宏是ANSYS宏命令，其主要功能是帮助用户方便地建立分析模型、方便地获取想要观察的分析结果。
目前，ANSYS提供了下列宏命令，可用于电磁场分析：·CMATRIX：计算导体间自有和共有电容系数·CURR2D：计算二维导电体内电流·EMAGERR：计算在静电或电磁场分析中的相对误差·EMF：沿预定路径计算电动力（emf）或电压降·FLUXV：计算通过闭合回路的通量·FMAGBC：对一个单元组件加力边界条件·FMAGSUM：对单元组件进行电磁力求和计算·FOR2D：计算一个体上的磁力·HFSWEEP：在一个频率范围内对高频电磁波导进行时谐响应分析，并进行相应的后处理计算·HMAGSOLV：定义2-D谐波电磁求解选项并进行谐波求解·IMPD：计算同轴电磁设备在一个特定参考面上的阻抗·LMATRIX：计算任意一组导体间的电感矩阵·MAGSOLV：对静态分析定义磁分析选项并开始求解·MMF：沿一条路径计算磁动力·PERBC2D：对2—D平面分析施加周期性约束·PLF2D：生成等势的等值线图·PMGTRAN：对瞬态分析的电磁结果求和·POWERH：在导体内计算均方根（RMS）能量损失·QFACT：根据高频模态分析结果计算高频电磁谐振器件的品质因子·RACE：定义一个“跑道形”电流源·REFLCOEF：计算同轴电磁设备的电压反射系数、驻波比、和回波损失·SENERGY：计算单元中储存的磁能或共能·SPARM：计算同轴波导或TE10模式矩形波导两个端口间的反射参数·TORQ2D：计算在磁场中物体上的力矩·TORQC2D：基于一个圆形环路计算在磁场中物体上的力矩·TORQSUM：对2-D平面问题中单元部件上的Maxwell力矩和虚功力矩求和本章对这些宏有详细描述。
在ANSYS命令手册和理论手册对这些宏有更详细的描述。
下面的表格列出了这些电磁宏的使用范畴。
1这些宏也应用于静电场问题2能用在通过界面单元INTER115连接的MVP区域11.2 使用电磁宏电磁宏根据其实现的功能，可以分为如下四类：·建模类·求解类·后处理类·高频分析类磁宏11.2.1 建模类有三个宏可用作帮助建模：RACE、PERBC2D和FMAGBC1）RACE产生一个由条形和弧形基元（SOURCE36单元）组成的“跑道”形电流源命令：RACEGUI：Main Menu>Preprocessor>-Modeling-Create>Racetrack CoilMainMenu>Preprocessor>Loads>-Loads-Apply>-Magnetic-Excitation>Racetrack CoilRACE宏要求的参数如前面图1所示。
“跑道”由二个参数XC和YC定位，这些值是在工作平面内分别沿X和Y轴到线圈厚度中点的距离。
执行该宏时，可以把构成线圈的这些SOURCE36单元定义为一个部件，将部件名作为该宏的一个输入参数即可。
2）PERBC2D宏通过生成两个周期性对称面所必须的约束方程或节点耦合来施加周期对称边界条件，调用该宏的方式如下：命令：PERBC2DGUI：MainMenu>Preprocessor>Loads>-Loads-Apply>-Magnetic-Boundary>-Vector Poten- Periodic BCs下面的图形描述了该宏的三种选项型式：奇对称选项表示一个半周期对称条件，偶对称条件表示全周期对称条件（重复结构）。
3）FMAGBC用于对单元组件施加Maxwell面标志和虚功边界条件：命令：FMAGBCGUI：Main Menu>Preprocessor>Loads>-Loads-Apply>-Magnetic-Flag> CompForce/TorqMain Menu>Solution>Apply>Comp. Force/Torq11.2.2 求解类有四个宏可帮助求解：MAGSOLV, HMAGSOLV, CMATRIX和LMATRIX11.2.2.1MAGSOLVMAGSOLV宏对大多数静磁分析问题能很快地定义求解选项并开始求解。
它可应用于2D和3D模型，标量势法、矢量势法和棱边单元求解方法，以及线性和非线性分析。
该宏不需要用户使用MAGOPT命令和二步或三步求解顺序（一定情况所要求），它也允许定义非线性收敛标准，并提供选项来控制电流源Biot-Savart 积分的重新计算。
命令：MAGSOLVGUI：Main Menu>Solution>-Solve-Electromagnet>-StaticAnalysis-Opt&Solv11.2.2.2HMAGSOLVHMAGSOLV宏对谐波分析能很快定义求解选项和开始求解。
对2-D模型，它使用磁矢势（MVP）方法求解。
它可用于线性和非线性分析。
对于非线性分析，此宏不需要定义二步求解过程，并允许用户自己定义收敛标准。
用下列方法之一，调用HMAGSOLV宏：命令：HMAGSOLVGUI：Main Menu>Solution>-Solve-Electromagnet>-HarmonicAnalys-Opt&Solv11.2.2.3 CMATRIXCMATRIX可计算“对地”和“集总”电容矩阵。
“对地”电容值表示一个导体的电荷与导体对地电压之比。
“集总”电容值表示二个导体之间的电容值。
实例详见多导体系统求取电容和本手册电容计算实例（命令方法）。
详细情况见ANSYS理论手册第五章。
用下面方法之一，调用CMATRIX宏命令：命令：CMATRIXGUI：Main Menu>Solution>Solve-Electromagnet>Capac Matrix11.2.2.4 LMATRIXLMATRIX宏可以计算任意线圈组中每个线圈的微分电感矩阵和总磁链。
参见《ANSYS理论手册》第5章。
LMATRIX宏用于在静磁场分析的一个“工作点”上计算任意一组导体间的微分电感矩阵和磁链。
“工作点”被定义为在系统上加工作（名义）电流所得到的解，该宏命令既可用于线性求解也可用于非线性求解。
必须用波前求解器来计算“工作点”的解。
LMATRIX宏的计算依赖于对工作点进行求解的过程中建立的多个文件。
该宏在执行求解之前在这些文件前面加一个前缀OPER来重命名文件，并在完成求解后自动保存这些文件。
用户自己也可以保存这些文件的拷贝以进行备份。
该宏命令返回一个N×N＋1矩阵参数，N×N部分表示N-绕组系统的微分电感值，此处N表示系统中的线圈数。
N＋1列表示总磁链。
第I行表示第I个线圈。
另外，电感矩阵的值还以文本文件的格式输出，以供外部使用。
文件中第一个列表表示每个线圈的磁链。
第二个列表表示微分电感矩阵的上三角部分。
命令：LMATRIXGUI：Main Menu>Solution>-Solve-Electromagnet>-StaticAnalysis-Induct Matrix在调用LMATRIX宏之前，还需要给线圈单元赋一个名义电流值。
对于使用磁矢势（MVP）法或基于棱边元方法进行求解的静磁分析，可以使用BFV、BFA或BFE命令来给线圈单元赋名义电流（以电流密度的方式）。
对于使用简化标势法（RSP）、差分标势法（DSP）和通用标势法（GSP）的静磁分析，可以使用SOURCE36单元的实常数来给线圈单元赋名义电流。
为了使用LMATRIX宏，必须事先用*DIM命令定义一个N阶数组，N为线圈数，数组的每行都表示一个线圈。
数组的值等于线圈在工作点时每匝的名义电流值，且电流值不能为零，当确实有零电流时，可以用一个很小的电流值来近似。
另外，还需用CM命令把每个线圈的单元组合成一个部件。
每组独立线圈单元的部件名必须是用一个前缀后面再加线圈号来定义。
一个线圈部件可由标量（RSP/DSP/GSP）或矢量单元（MVP）混合组成，最重要的一点是这些单元的激励电流与前面数组中所描述的电流相同。
在LMATRIX宏中需定义一个用于保存电感矩阵的数组名，用LMATRIX宏的对称系数（symfac）来定义对称性。
如果由于对称性而只建了n分之一部分模型，则计算出的电感乘以n就得到总的电感值。
当工作点位于BH曲线的弯点处时，切向磁导率变化最快，会导致计算的感应系数随收敛标准而变化。
为了获得更加准确的解，收敛标准要定义得更加严格一些，不仅仅是缺省值1.0×10－3。
一般在执行MAGSOLV命令时，选择1.0×10－4或1.0×10－5。
在使用LMATRIX命令前，不要施加（或删除）非均匀加载，非均匀加载由以下原因生成：·自由度命令(D, DA,等)在节点或者实体模型上定义非0值·带有非0约束的CE命令不要在不包含在单元组件中的单元上施加任何载荷(如current)下面的例子是一个3线圈系统，每个线圈的名义电流分别为1.2、1.5和1.7安/匝，其分析的命令流如下。
在这个例子中，数组名为“curr”，线圈部件名前缀为“wind”，电感矩阵的计算值存贮在名为“ind”数组中。
值得注意的是，在LMATRIX命令行中，这些名字必须用单引号引起来。
*dim，cur，，3！3个线圈系统数组cur（1）=1.2！线圈1的名义电流为1.2安培/匝cur（2）=1.5！线圈2的名义电流为1.5安培/匝cur（3）=1.7！线圈3的名义电流为1.7安培/匝esel，s……！选择线圈1的单元cm，wind1，elem！给选出的单元赋予部件名wind1esel，s……！选择线圈2的单元cm，wind2，elem！给选出的单元赋予部件名wind2esel，s……！选择线圈3的单元cm，wind3，elem！给选出的单元赋予部件名wind3symfac=2！对称系数Imaxtrix，symfac，’wind’，’curr’，’ind’ ！计算微分电感矩阵和总磁链*stat，ind！列出ind电感矩阵11.2.2.5 下面是以命令流方式进行的一个计算电感矩阵的例子该例计算一个二线圈系统（永磁电感器件）在非线性工作点下的微分电感矩阵和总磁链，其示意图如下：几何性质：x1=0.1, x2=0.1, x=0.1, y=0.1材料性质：μr =1.0（空气），Hc=25（永磁体），B-H曲线（永磁体，见输入参数）线圈1：名义电流＝0.25安/匝，匝数＝10线圈2：名义电流＝0.125安/匝，匝数＝20目标值：L11=4, L22=16, L12=8命令流如下：/batch,list/title, Two-coil inductor with a permanent magnet /nopr!geometry data!n=1! meshing parameterx=0.1! width (x size) of corey=0.1! hight of core, y size of windowz=1! thickness of iron in z directionx1=0.1! width (x size) of coil 1x2=0.1! width (x size) of coil 2Hcy=25! coercive magnetic field in y directionn1=10! number of turns in coil1n2=20! number of turns in coil2!!excitation data used by LMATRIX.MAC!symfac=1! symmetric factor for inductance computation nc=2! number of coils*dim,cur,array,nc! nominal currents of coils*dim,coils,char,nc! names of coil components!cur(1)=0.25! nominal current of 1st coilcoils(1)="wind1"! name of coil 1 component!cur(2)=-0.125! nominal current of 2nd coilcoils(2)="wind2"! name of coil 2 component!!auxiliary parameters!mu0=3.1415926*4.0e-7x3=x1+x2! x coordinate right to coil2 leftx4=x3+2*x! x coordinate right to corex5=x4+x2! x coordinate right to coil2 rightx6=x5+x1! x coordinate right to coil1 rightjs1=cur(1)*n1/(x1*y)! nominal current density of coil1 js2=cur(2)*n2/(x2*y)! nominal current density of coil2 !/prep7et,1,53!mp,murx,1,1! air/coilmp,mgyy,2,Hcy! coercive termBs=2! saturation flux densityHs=100! saturation magnetic fieldTB,BH,2! core: H = Hs (B/Bs)^2; BS=2T;HS=100A/m*do,qqq,1,20B=qqq/10*Bstbpt,,Hs*(B/Bs)**2,B*enddo!rect, 0,x1,0,y! coil1 leftrect,x1,x3,0,y! coil2 leftrect,x3,x4,0,y! corerect,x4,x5,0,y! coil2 rightrect,x5,x6,0,y! coil1 right!aglue,all!asel,s,loc,x,x1/2! coil 1 volume attributeaatt,1,1,1asel,s,loc,x,x5+x1/2aatt,1,2,1asel,s,loc,x,x1+x2/2! coil 2 volume attributeaatt,1,3,1asel,s,loc,x,x4+x2/2aatt,1,4,1asel,s,loc,x,x3+x! iron volume attributeaatt,2,5,1asel,all!esize,,namesh,all!nsel,s,loc,x,x6! flux parallel Dirichlet at symmetry plain, x=x6 !! homogeneous Neumann flux normal at yoke, x=0d,all,az,0nsel,all!esel,s,real,,1! coil 1 left componentbfe,all,JS,,,,js1! unite current density in coil 1!esel,s,real,,2! coil 1 right componentbfe,all,JS,,,,-js1! return unite current density in coil 1 !esel,s,real,,1,2cm,coils(1),elem!esel,s,real,,3! coil 2 left componentbfe,all,JS,,,,js2! unite current density in coil 2!esel,s,real,,4! coil 2 right componentbfe,all,JS,,,,-js2! return unite current density in coil 2 !esel,s,real,,3,4cm,coils(2),elem!!allsel!fini!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! /com/com obtain operating solution/com!/solucnvtol,csg,,1.0e-4/out,scratchsolvefini!/post1!/out!/com,/com,senergy,! Stored electromagnetic energy savelen=S_ENGsenergy,1! Co-energysavelce=C_ENG!fini!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! compute inductancelmatrix,symfac,"wind","cur","ind", ! compute inductance matrix and flux !/comfinish你将得到如下结果：SUMMARY OF STORED ENERGY CALCULATIONLoad Step Number:1.Substep Number:1.Time:0.1000E+01Material Number ofStored EnergyMaterial DescriptionNumberElements(J/m)1.4.0.52360E-05LinearIsotrp...2.1.-0.33314E+00Nonlin.MagnetIsotrp._____________________________________________________________________ T O T A L5.-0.33313E+00Note:The energy density for the active elements used in the energy calculation is stored in the element item "MG_ENG" for displayand printing. The total stored energy is saved as parameter (S_ENG) _____________________________________________________________________ 本文系e-works专稿，未经授权严禁转载SUMMARY OF COENERGY CALCULATIONLoad Step Number:1.Substep Number:1.Time:0.1000E+01Material Number ofCoenergyMaterial DescriptionNumberElements(J/m)1.4.0.52360E-05LinearIsotrp...2.1.0.33314E+00Nonlin.MagnetIsotrp._____________________________________________________________________T O T A L5.0.33314E+00Note:The co-energy density for the active elements used in the co-energy calculation is stored in the element item "MG_COENG" for displayand printing. The total coenergy is saved as parameter (C_ENG)_____________________________________________________________________________________ LMATRIX SOLUTION SUMMARY ___________________Flux linkage of coil1. =0.19989E+01Flux linkage of coil2. =0.39978E+01Self inductance of coil1. =0.39976E+01Self inductance of coil2. =0.15989E+02Mutual inductance between coils1. and2. =0.79948E+01Inductance matrix is stored in array parameter ind( 2., 3.)Inductance matrix is stored in file ind.txt11.2.3 后处理类1）TORQ2D沿一条预先定义好的路径用面积分计算在磁场内一个物体上的力矩。
