空间中的线线平行

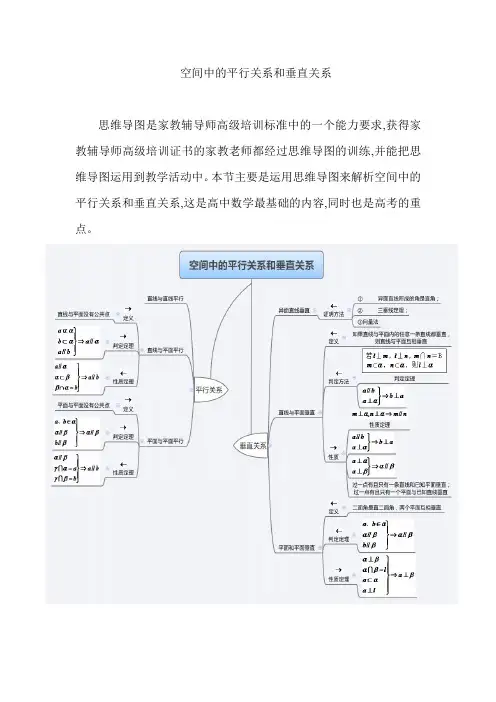
空间中的平行关系和垂直关系思维导图是家教辅导师高级培训标准中的一个能力要求,获得家教辅导师高级培训证书的家教老师都经过思维导图的训练,并能把思维导图运用到教学活动中。

本节主要是运用思维导图来解析空间中的平行关系和垂直关系,这是高中数学最基础的内容,同时也是高考的重点。

一、空间中的平行关系线线平行 平行 线面平行 面面平行 1、直线与平面平行定义：直线与平面没有公共点，则直线与平面平行。

判定定理：如果平面外一条直线和这个平面内一条直线平行，那么这条直线和 这个平面平行。

符号语言表示：ααα////a b a b a ⇒⎪⎭⎪⎬⎫⊂⊄证法一：∵a ∥b ，∴a 、b 确定一个平面，设为β. ∴a ⊂β，b ⊂β∵a ⊄α，a ⊂β ∴α和β是两个不同平面. ∵b ⊂α且b ⊂β ∴α∩β＝b 假设a 与α有公共点P则P ∈α∩β＝b ，即点P 是a 与b 的公共点，这与已知a ∥b 矛盾 ∴假设错误，故a ∥α.证法二：假设直线a 与平面α有公共点P ， 则点P ∈b 或点P ∉b若点P ∈b ，则a ∩b ＝P ，这与a ∥b 矛盾. 若点P ∉b ，又b ⊂α，a ∩α＝P由于与平面相交的直线和这个平面内不过交点的直线是异面直线 ∴a 、b 异面，这与a ∥b 也矛盾 综上所述，假设错误，故a ∥α.证法三：假设a ∩α＝P . ∵a ∥b ， ∴P ∉b在面α内过P 作c ∥b 则c ∥a ，这与a ∩c ＝P 矛盾. ∴假设错误，故a ∥α. 证法四：∵a ∥b ，∴a 、b 确定一个平面，设为β∴a ⊂β，b ⊂β ∵a ⊄α，a ⊂β∴α、β是两个不同的平面∵b ⊂α，又b ⊂β ∴α∩β＝b∵a 与b 没有公共点 ∴a 与α没有公共点 (若有公共点，公共点必在b 上，则与a ∥b 矛盾). ∴a ∥α.性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行.符号语言表示：b a b a ////⇒⎪⎭⎪⎬⎫=⋂⊂αββαα⎪⎪⎪⎭⎪⎪⎪⎬⎫⊂⊂=⋂⇒⎭⎬⎫⊂⇒=⋂ββφααβαb a b a a b b // 证明：⇒a ∥b2、平面与平面平行定义：两个平面没有公共点就叫做两个平面平行。

空间几何的平行与垂直判定空间几何是数学中的一个重要分支，涉及到直线、平面、点等概念的研究。

其中，平行和垂直是空间几何中常见的关系，本文将对平行和垂直的判定方法进行详细介绍。

一、平行的判定方法在空间几何中，平行是指两个线(线段)或两个平面永远不会相交的关系。

下面将介绍几种常见的平行判定方法。

1. 直线的平行判定给定两条直线l1和l2，如果它们的斜率相等且不相交，则可以判定l1与l2平行。

即若直线l1的斜率为k1，直线l2的斜率为k2，且k1≠k2时，则l1和l2平行。

2. 平面的平行判定对于两个平面P1和P2，如果它们的法向量相等或平行，则可以判定P1与P2平行。

二、垂直的判定方法在空间几何中，垂直是指两个线(线段)或两个平面之间的相互垂直关系。

下面将介绍几种常见的垂直判定方法。

1. 直线的垂直判定给定两条直线l1和l2，如果它们的斜率互为倒数且不相交，则可以判定l1与l2垂直。

即若直线l1的斜率为k1，直线l2的斜率为k2，并且k1·k2=-1时，则l1和l2垂直。

2. 平面的垂直判定对于两个平面P1和P2，如果它们的法向量互为倒数且不平行，则可以判定P1与P2垂直。

三、平行与垂直的应用举例平行和垂直关系在实际问题中经常被应用。

以下是几个应用举例。

1. 平行线与垂直线的交点问题当两条平行线相交时，它们的交点无穷多个；而当两条垂直线相交时，它们的交点只有一个。

这一性质在导弹拦截等领域具有重要意义。

2. 平行四边形及其性质平行四边形是指具有两对平行边的四边形。

它们的特点是相对边相等、对角线相交于对角线的中点、对角线互相平分等。

平行四边形的性质在建筑设计等领域有广泛应用。

3. 垂直投影与三视图在工程绘图中，垂直投影是指将物体在垂直方向上的投影。

根据垂直投影可以得到物体的平面图、前视图、左视图、右视图等，这些视图通常用于工程设计、建筑规划等领域。

4. 共线与共面条件若一条直线与一个平面相交，那么这条直线上的任意一点与该平面上的任意一点以及该平面上的任意一条直线都共线。

空间向量中证明线线平行的公式
在空间向量中，我们经常需要判断两条线是否平行。

判断两条
线是否平行的一种方法是使用向量的方法。

下面我们将介绍如何使
用向量来证明两条线是否平行的公式。

假设有两条线，分别用参数方程表示为:
L1: r1 = a + λv.
L2: r2 = b + μw.
其中a和b是两条线上的已知点，v和w是两条线的方向向量，λ和μ是参数。

要证明L1和L2平行，我们可以使用以下方法：
1. 首先，我们可以计算两条线的方向向量v和w。

2. 然后，我们可以计算v和w的向量积（叉乘）v × w。

3. 最后，我们可以判断v × w是否为零向量。

如果v × w为零向量，那么根据向量积的性质，我们可以得出结论，两条线平行。

证明过程如下：
v × w = 0。

⇒ |v × w| = 0。

⇒ |v| |w| sinθ = 0。

其中θ为v和w之间的夹角。

根据向量积的性质，v × w = 0 当且仅当v与w共线或其中一个为零向量。

因此，如果v × w = 0，则L1和L2平行。

通过这种方法，我们可以使用向量来证明两条线是否平行的公式。

这种方法简单直观，适用于空间向量中线线平行的判断。

希望这篇文章能对你有所帮助。

空间几何中的平行关系在我们所接触的空间几何世界里，平行关系是一个非常重要的概念。

它不仅在数学理论中有着关键的地位，还在实际生活和其他学科领域有着广泛的应用。

首先，让我们来理解一下什么是线线平行。

如果在同一平面内，两条直线永远不会相交，那么我们就说这两条直线是平行的。

比如，在笔直的公路上，两条路边线就是平行的。

线线平行有许多判定定理，其中一个常见的就是同位角相等，两直线平行。

比如说，有两条被第三条直线所截的直线，如果同位角的度数相等，那么这两条直线就是平行的。

接下来，我们看看线面平行。

一条直线和一个平面，如果没有公共点，那就称这条直线与这个平面平行。

想象一下，天花板上的吊灯线和地板所在的平面，它们通常是没有交点的，这就是线面平行的一个例子。

那如何判断一条直线是否与一个平面平行呢？如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行。

这就好比在一个房间里，一条在墙外的直线和房间地面上的某条直线平行，那么墙外的这条直线就和地面所在的平面平行。

再说说面面平行。

如果两个平面没有公共点，就称这两个平面平行。

比如，我们常见的楼房中，一层楼的天花板和下一层楼的地板，这两个平面通常就是平行的。

那怎样才能知道两个平面是不是平行呢？一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

就好像在一个平面内有两条相交的直线，它们分别和另一个平面内的两条直线平行，那么这两个平面就是平行的。

在解决空间几何中的平行关系问题时，我们常常需要进行一些推理和证明。

比如说，要证明线面平行，我们可能需要先找到平面内与已知直线平行的那条直线。

这就需要我们对已知条件进行仔细的分析和运用各种定理。

平行关系在实际生活中的应用也非常广泛。

建筑设计中，为了保证建筑物的结构稳定和美观，常常会利用平行关系。

比如，柱子之间的平行线能够增强建筑物的稳定性；窗户的边框平行能够使窗户看起来更加整齐美观。

在机械制造中，平行的部件能够保证机器的正常运转，减少摩擦和损耗。

班级姓名考号
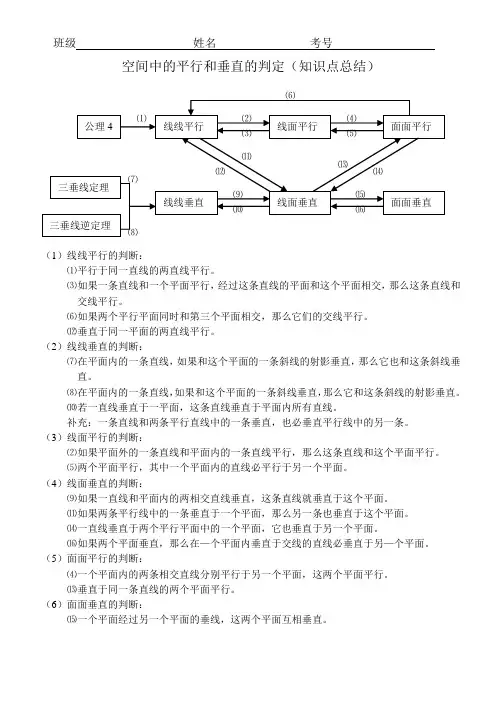
空间中的平行和垂直的判定（知识点总结）
（1）线线平行的判断：
⑴平行于同一直线的两直线平行。

⑶如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和
交线平行。

⑹如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

⑿垂直于同一平面的两直线平行。

（2）线线垂直的判断：
⑺在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂
直。

⑻在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它和这条斜线的射影垂直。

⑽若一直线垂直于一平面，这条直线垂直于平面内所有直线。

补充：一条直线和两条平行直线中的一条垂直，也必垂直平行线中的另一条。

（3）线面平行的判断：
⑵如果平面外的一条直线和平面内的一条直线平行，那么这条直线和这个平面平行。

⑸两个平面平行，其中一个平面内的直线必平行于另一个平面。

（4）线面垂直的判断：
⑼如果一直线和平面内的两相交直线垂直，这条直线就垂直于这个平面。

⑾如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面。

⒁一直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。

⒃如果两个平面垂直，那么在—个平面内垂直于交线的直线必垂直于另—个平面。

（5）面面平行的判断：
⑷一个平面内的两条相交直线分别平行于另一个平面，这两个平面平行。

⒀垂直于同一条直线的两个平面平行。

（6）面面垂直的判断：
⒂一个平面经过另一个平面的垂线，这两个平面互相垂直。

空间平行方法总结
平行关系：线线平行、线面平行、面面平行
线线平行：两直线平行必定共面，所以线线平行问题在空间中只是作为证明线面平行或者面面平行的工具使用，不会直接考查。

常见的线线平行有：（1）平行四边形对边平行；（2）三角形的中位线平行对应边；（3）两平行平面与第三个平面相交，则两条交线平行（面面平行的性质定理）；（4）垂直于同一平面的两直线平行；（5）如果一条直线和一个平面平行，经过这条直线的平面和这条直线相交，那么这条直线和交线平行（线面平行的性质定理）；（6）平行的传递性；
线面平行：线面平行判定定理为，平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行。

所以线面平行的核心归结为证明线线平行。

面面平行：面面平行的判定定理为，一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

既证明两平面平行只需证明两条相交线与一个平面平行即可，所以面面垂直归结为线线垂直。

总结：在空间平行关系中主要为:线线平行、线面平行、面面平行，考查题目主要类型为线面平行和面面平行，面面平行通过证明两组线面平行，线面平行通过证明线线平行，所以要熟练掌握线线平行的证明，也是空间中平行的核心内容。

2023年高考数学考点复习——空间几何中的平行证明考点一、线线平行例1、如图，在四面体ABCD 中，E ，F 分别为DC ，AC 的中点，过EF 的平面与BD ，AB 分别交于点G ，H .求证：//EF GH证明：因为E ，F 分别为DC ，AC 的中点，所以//AD EF ，因为AD ⊄平面EFHG ，EF ⊂平面EFHG所以//AD 平面EFHG又平面EFHG ⋂平面ABD HG =，AD ⊂平面ABD所以//AD GH ，所以//EF GH .例2、如图，在四棱锥S -ABCD 中，底面ABCD 是菱形，60BAD ∠=︒，SAB ∆为等边三角形，G 是线段SB 上的一点，且SD //平面GAC .求证：G 为SB 的中点证明：证明：如图，连接BD 交AC 于点E ，则E 为BD 的中点，连接GE ，∵//SD 平面GAC ，平面SDB 平面=GAC GE ，SD ⊂平面SBD ，∵//SD GE ，而E 为BD 的中点，∵G 为SB 的中点.例3、在正四棱锥P ABCD -中，,E F 分别是,AB AD 的中点，过直线EF 的平面α分别与侧棱,PB PD 交于点,M N ，求证：//MN BD证明：证明：在ABD △中，因为E ，F 分别是,AB AD 的中点，所以EF BD ∕∕且12EF BD =， 又因为EF ⊄平面PBD ，BD ⊂平面PBD ，所以//EF 平面PBD因为EF ⊂平面,αα⋂平面PBD MN =，所以//EF MN ，所以//MN BD ．跟踪练习 1、如图，四边形ABCD 和三角形ADE 所在平面互相垂直，//AB CD ，AB BC ⊥，60DAB ∠=︒，4AB AD ==，AE DE ⊥，AE DE =，平面ABE 与平面CDE 交于EF ，求证：//CD EF证明：证明：因为//AB CD ，AB平面ABE ，CD ⊄平面ABE ，所以//CD 平面ABE ， 因为平面ABE 平面CDE EF =，CD ⊂平面CDE ，所以//CD EF .2、在四棱锥P ﹣ABCD 中，底面ABCD 为平行四边形E ，F 分别为BC ，AD 的中点，过EF 的平面与平面PCD 交于M ，N 两点，求证：//AB MN答案：证明见解析证明：∵底面ABCD 为平行四边形，E ，F 分别为BC ，AD 的中点，∵EF //CD ，∵EF //AB .EF ⊄平面PCD ，CD ⊂平面PCD ，所以//EF 平面PCD ，过EF 的平面与平面PCD 交于M ，N 两点，∵MN //EF ，∵AB //MN .3、如图，三棱锥P ABC -中，∵ABC 为正三角形，点1A 在棱PA 上，1B 、1C 分别是棱PB 、PC 的中点，直线11A B 与直线AB 交于点D ，直线11A C 与直线AC 交于点E ，求证：//DE BC证明：∵1B 、1C 分别是棱PB 、PC 的中点，∵11//B C BC ，∵11B C ⊄平面BCDE ，BC ⊂平面BCDE ，∵11//B C 平面BCDE ，∵11B C ⊂平面11B C DE ，平面BCDE ⋂平面11B C DE DE =，∵11//B C DE ，则//DE BC ；4、如图，四棱锥P ABCD -的底面是边长为8的正方形，点G.E.F .H 分别是棱PB ．AB ．DC ．PC 上共面的四点，//BC 平面GEFH.证明：//GH EF证明：∵//BC 平面GEFH ，又∵BC ⊂平面PBC 且平面PBC平面GEFH GH =，∵//BC GH .又∵//BC 平面GEFH ，又∵BC ⊂平面ABCD 且平面ABCD平面GEFH EF =，∵//BC EF ，∵//EF GH .5、如图，AE ⊥平面ABCD ，//BF 平面ADE ，//CF AE ，求证：//AD BC证明：依题意//CF AE ，CF ⊄平面ADE ，AE ⊂平面ADE ，∵//CF 平面ADE ，又//BF 平面ADE ，BF CF F ⋂=，∵平面//BCF 平面ADE ，∵平面BCF ⋂平面ABCD AD =，平面ADE平面ABCD BC =，∵//AD BC ；考点二、 线面平行例1、如图，正三棱柱ABC ﹣A 1B 1C 1中D 是AC 的中点，求证：B 1C ∵平面A 1BD证明：设AB 1与A 1B 相交于点P ，连接PD ，则P 为AB 1中点，∵D 为AC 中点，∵PD ∵B 1C ，又∵PD ∵平面A 1BD ，B 1C ⊄平面A 1BD ，∵B 1C ∵平面A 1BD例2、如图，在四棱锥A BCDE -中，底面BCDE 为矩形，M 为CD 中点，连接,BM CE 交于点,F G 为ABE △的重心，证明：//GF 平面ABC证明：延长EG 交AB 于N ，连接CN ，因为G 为ABE △的重心，则N 为AB 的中点，且2EG GN =， 因为//CM BE ，所以2EF BE FC CM ==，所以2EF EG FC GN==，因此//GF NC ， 又因为GF ⊄平面ABC ，NC ⊂平面ABC ，所以//GF 平面ABC ；例3、如图，四棱锥C ABED -中，四边形ABED 是正方形，若G ，F 分别是线段EC ，BD 的中点.（1）求证：//GF 平面ABC .证明：由四边形ABED 为正方形可知，连接AE 必与BD 相交于中点F ，又G 是线段EC 的中点，故//GF AC ，GF ⊄面ABC ，AC ⊂面ABC ，//GF ∴面ABC ；跟踪练习1、如图，在直三棱柱111ABC A B C -中，底面ABC 是等边三角形，D 是AC 的中点，证明：1//AB 平面1BC D证明：直三棱柱111ABC A B C -中，设1B C 与1BC 交于点E ，连接DE ，四边形11BCC B 是矩形，则E 为1B C 的中点，因D 是AC 的中点，所以1//DE AB ，又1AB ⊄平面1BC D ，DE ⊂平面1BC D ，所以1//AB 平面1BC D . 2、《九章算术》是我国古代的数学著作，是“算经十书”中最重要的一部，它对几何学的研究比西方要早1000多年.在《九章算术》中，将底面为直角三角形，且侧棱垂直于底面的三棱柱称为堑堵.如图，在堑堵111ABC A B C -中，，11AA AB AC ===，M ，N 分别是1CC ，BC 的中点，点P 在线段11A B 上，若P 为11A B 的中点，求证：//PN 平面11AAC C证明：证明：取11A C 的中点H ，连接PH ，HC .在堑堵111ABC A B C -中，四边形11BCC B 为平行四边形，所以11//B C BC 且11B C BC =.在111A B C △中，P ，H 分别为11A B ，11A C 的中点，所以11//PH B C 且1112PH B C =.因为N 为BC 的中点，所以12NC BC =， 从而NC PH =且//NC PH ， 所以四边形PHCN 为平行四边形，于是//PN CH .因为CH ⊂平面11AC CA ，PN ⊄平面11AC CA ，所以//PN 平面11AACC .3、如图，直四棱柱1111ABCD A B C D -的底面是菱形，12AA =，1AB =，E ，M ，N 分别是BC ，1BB ，1A D 的中点，证明：//MN 平面ABCD证明：连接1,ME B C ，,E M 分别为1,BC BB 中点，11//2ME B C ∴； 由直四棱柱特点知：11//A D B C ，11//2ME A D ∴，又N 为1A D 中点，//ME ND ∴， ∴四边形MNDE 为平行四边形，//MN DE ∴，又DE ⊂平面ABCD ，MN ⊄平面ABCD ，//MN ∴平面ABCD ；4、如图，在四棱锥P ABCD -中，四边形ABCD 是边长为2的菱形，M 是AB 的中点，N 是PD 的中点，PA AB =，求证：//MN 平面PBC证明：如图∵，取PC 的中点Q ，连接BQ ，NQ ，因为N 是PD 的中点，所以//NQ CD 且12NQ CD =.因为四边形ABCD 是菱形，M 是AB 的中点，所以//BM CD 且12BM CD =， 从而//BM NQ 且BM NQ =，所以四边形BMNQ 是平行四边形，从而//MN BQ .又MN ⊄平面PBC ，BQ ⊂平面PBC ，所以//MN 平面PBC . 5、如图，已知四边形ABCD 和BCEG 均为直角梯形，//AD BC ，//CE BG ，且2BCD BCE π∠=∠=，222BC CD CE AD BG =====，）求证：//AG 平面BDE答案：证明见解析证明：证明：过G 作GN CE ⊥于N ，交BE 于M ，连接DM ，如图所示：因为BC CE ⊥，且2CE BG =，所以N 为CE 中点，所以MG MN =，MNBC DA ，12MN AD BC ==， 所以MG AD ，MG AD =，所以四边形ADMG 为平行四边形，所以AG DM ，又DM ⊂平面BDE ，AG ⊄平面BDE ，所以AG 平面BDE .6、在四棱锥P —ABCD 中，AB //CD ，过CD 的平面分别交线段P A ，PB 于M ，N ，E 在线段DP 上(M ，N ，E 不同于端点)求证：CD //平面MNE证明：证明：∵//AB CD ，AB ⊂平面ABP ，CD ⊄平面ABP ∵//CD 平面ABP又∵CD ⊂平面CDMN ，平面CDMN 平面ABP MN =∵//CD MN又∵MN ⊂平面MNE ，CD ⊄平面MNE ∵//CD 平面MNE7、如图，在多面体ABCDEF 中，矩形BDEF 所在平面与正方形ABCD 所在平面垂直，1AB =，点M 为AE 的中点，求证：//BM 平面EFC证明：连接AC 交BD 于点N .连接MN .因为四边形ABCD 是正方形，所以N 为AC 的中点，由于M 为AE 的中点，所以//MN CE ， 又因为MN ⊄平面CEF ，CE ⊂平面CEF ，所以//MN 平面CEF ，易知//BN EF ，BN ⊄平面CEF ，EF ⊂平面CEF ，所以//BN 平面CEF ，因为MN BN N ⋂=，BN ⊂平面BMN ，MN ⊂平面BMN ，所以平面//BMN 平面CEF .又因为BM ⊂平面BMN ，所以//BM平面EFC ；8、在四棱锥P ABCD -中，底面ABCD 为梯形，//AB CD ，22AB CD ==，若Q 为AB 的中点，求证：//DQ 平面PBC证明：∵在梯形ABCD 中，//AB CD ，22AB CD ==，Q 为AB 的中点，所以//BQ CD 且BQ CD =，∵四边形BCDQ 为平行四边形，所以//DQ BC ，∵BC ⊂平面PBC ，DQ ⊄平面PBC ，所以//DQ 平面PBC ．9、如图所示，四面体P ABC 中，E ，F 分别为AB ，AC 的中点，过EF 作四面体的截面EFGH 交PC 于点G ，交PB 于点H ，证明：GH /平面ABC证明：∵E ，F 分别为AB ，AC 的中点,∵EF ∵BC ,又∵EF ∵平面PBC ,BC ∵平面PBC ,∵EF ∵平面PBC ,∵EF ∵平面EFGH ,平面EFGH ∩平面PBC =GH ,∵EF ∵GH ,又∵GH ∵平面ABC ,EF ∵平面ABC ,∵GH ∵平面ABC ;10、如图所示，在三棱柱111ABC A B C -中，D 为AC 的中点，求证：1//AB 平面1BC D证明：证明：如图，连接1B C 交1BC 于O ，连接OD ，∵四边形11BCC B 是平行四边形．∵点O 为1B C 的中点．∵D 为AC 的中点，∵OD 为1AB C 的中位线，∵1//OD AB ．∵OD ⊂平面1BC D ，1AB ⊄平面1BC D ，∵1//AB 平面1BC D ．11、如图，在四棱锥P ABCD -中，底面ABCD 是边长为2的正方形，PAB △为正三角形，且侧面PAB ⊥底面ABCD ，M 为PD 的中点，求证：//PB 平面ACM答案：证明见解析证明：证明：连接BD ，与AC 交于O ，在PBD △中，,O M 分别为,BD PD 的中点，//BP OM ∴,BP ⊄平面,ADE OM ⊂平面CAM ，//BP ∴平面CAM ；12、如图，在三棱柱111ABC A B C -中，侧面11ABB A 是菱形，E 是棱1BB 的中点，CA CB =，F 在线段AC 上，且2AF FC =，证明：1//CB 平面1A EF答案：证明见解析证明：连接1AB 交1A E 于点G ，连接FG ，因为四边形11ABB A 为菱形，则11//AA BB 且11AA BB =， E 为1BB 的中点，则11//B E AA 且1112B E AA =，故11112B G B E AG AA ==， 所以，1B G CF AG AF=，1//CB FG ∴， 1CB ⊄平面1A EF ，FG ⊂平面1A EF ，因此，1//CB 平面1A EF ；考点三、 面面平行例1、如图所示，四棱柱1111ABCD A B C D -的侧棱与底面垂直，12,,AC AA AD DC AC BD ====交于点E ，且,E F 分别为1,AC CC的中点，2BE =，求证：平面11//B CD 平面1A BD证明：如图，连接1AD ，设11AD A D H ⋂=，则H 为1AD 的中点，而E 为AC 的中点，连接EH ，则EH为1ACD △的中位线，所以1//EH CD ，又EH ⊄平面11B CD ，1CD ⊂平面11B CD ，所以//EH 平面11B CD ，又因为侧棱与底面垂直，所以1111//,=BB DD BB DD ，所以四边形11BB D D 为平行四边形，所以11//B D BD ，BD ⊄平面11B CD ，11B D ⊂平面11B CD ，所以//BD 平面11B CD ，又BD EH E ⋂=，,BD EH ⊂平面1A BD ，所以平面11//B CD 平面1A BD .例2、如图，在三棱锥P ABC -中，PAB △是正三角形，G 是PAB △的重心，D ，E ，H 分别是PA ，BC ，PC 的中点，点F 在BC 上，且3BF FC =，求证：平面//DFH 平面PGE证明：连结BG ，因为PAB △是正三角形，G 是PAB △的重心，D 为PA 的中点，所以BG 与GD 共线，且2BG GD =，因为E 为BC 的中点，3BF FC =，所以F 是CE 的中点， 所以2BG BE CD EF==，所以//GE DF ， 又GE平面PGE ，DF ⊄平面PGE ，所以//DF 平面PGE ， 因为H 是PC 的中点，所以FH //PE ，因为FH ⊄平面PGE ，PE ⊂平面PGE ，所以//FH 平面PGE ，因为FH DF F ⋂=，,FH DF ⊂平面DFH ，所以平面//DFH 平面PGE ；例3、如图，在多面体ABCDEF 中，ABCD 是正方形，2//AB DE BF BF DE ==，，，M 为棱AE 的中点，求证：平面//BMD 平面EFC证明：如图，连接AC ，交BD 于点N ，∵N 为AC 的中点，连接MN ，由M 为棱AE 的中点，则//MN EC ．∵MN ⊄面EFC ，EC ⊂面EFC ，∵//MN 平面EFC ．∵//BF DE BF DE =，，∵四边形BDEF 为平行四边形，∵//BD EF ．又BD ⊄平面EFC ，EF ⊂平面EFC ，∵//BD 平面EFC ，又MNBD N =， ∵平面//BMD 平面EFC ．跟踪练习1、如图，在几何体ABCDE 中，四边形ABCD 是矩形，2AB BE EC ===，G ，F ，M 分别是线段BE ，DC ，AB 的中点，求证：平面//GMF 平面ADE证明：如图，因为AB中点为M，连接MG，∥，又G是BE的中点，可知GM AE又AE⊆平面ADE，GM⊄平面ADE，所以GM平面ADE．在矩形ABCD中，由M，F分别是AB，CD的中点得MF AD．又AD⊆平面ADE，MF⊄平面ADE，所以MF平面ADE．⋂=，GM⊆平面GMF，MF⊆平面GMF，又因为GM MF M所以平面GMF平面ADE2、如图，四边形ABCD是边长为BB1＝DD1＝2，E，F分别是AD1，AB1的中点，证明：平面BDEF∵平面CB1D1证明：证明：连接AC ，交BD 于点O ，连接OE ，则O 为AC 的中点，∵E 是1AD 的中点，1//OE CD ∴OE ⊂平面BDEF ,1CD ⊄平面BDEF ,所以1//CD 平面BDEF又F 是1AB 的中点11//EF B D ∴EF ⊂平面BDEF ,11B D ⊄平面BDEF ,所以11//B D 平面BDEF又111,CD B D ⊂平面11CB D ,1111B D CD D ⋂=, 所以平面//BDEF 平面11CB D ．3、如图，已知矩形ABCD 所在的平面垂直于直角梯形ABPE 所在的平面，且EP =2BP =，1AD AE ==，AE EP ⊥，//AE BP ，F ，G 分别是BC ，BP 的中点，求证：平面//AFG 平面PEC证明：∵F ，G 分别是BC ，BP 的中点，∵FG CP ，且FG ⊄平面CPE ，则FG ∥平面CPE ，1BG PG AE ===，且//AE BP ，AE EP ⊥∵四边形AEPG 是矩形，则EP AG ∥，且AG ⊄平面CPE ，则AG平面CPE又GA GF G ⋂=，故平面//AFG 平面PEC4、如图，在四棱锥S -ABCD 中，底面ABCD 是直角梯形，AD //BC ，P ，Q 是AB ，CD 的中，点M ，N 分别是SB ，CB 的中点，求证∵平面AMN //平面SCD答案：证明见解析证明：因为M 、N 分别是SB ，CB 的中点，所以//MN SC ，MN ⊄面SCD ，SC ⊂面SCD ，所以//MN 面SCD ，又//AD CN 且AD CN =，所以ADCN 为平行四边形，所以//AN DC ，AN ⊄面SCD ，DC ⊂面SCD ，所以//AN 面SCD ，又AN MN N =，,AN MN ⊂面AMN ，所以面//AMN 面SCD ；5、如图，在三棱锥P ABC -中，PAB △是正三角形，G 是PAB △的重心，,,D E H 分别是,,PA BC PC 的中点，点F 在BC 上，且3BF FC =，求证：平面//DFH 平面PGE证明：证明：连结BG ，由题意可得BG 与GD 共线，且2BG GD =，∵E 是BC 的中点，3BF FC =，∵F 是CE 的中点，∵2BG BE GD EF==，∵//GE DF ，GE 平面PGE ；DF ⊄平面PGE ；∵//DF 平面PGE ， ∵H 是PC 的中点，∵//FH PE ，PE ⊂平面PGE ，FH ⊄平面PGE ；∵//FH 平面PGE ， ∵DF FH F =，DF ⊂平面DEF ，FH ⊂平面DEF ，∵平面//DFH 平面PGE ； 考点四 平行中的动点例1、直三棱柱111ABC A B C -所有棱长都为2，在AB 边上是否存在一点E ，使1//AC 平面1CEB ，若存在给出证明，若不存在，说明理由证明：存在，E 是AB 的中点，直三棱柱111ABC A B C -中，连接1BC 交1B C 于点O ，如图：则O 为1BC 中点，连接OE ，而E 为AB 的中点，则1//OE AC ，又1AC ⊄平面1CEB ，OE ⊂平面1CEB ，所以1//AC 平面1CEB ；例2、如图，在三棱柱111ABC A B C -中，1AA ⊥平面ABC ，90ACB ∠=︒，CA CB ==，1AA =D 是棱11A B 的中点，E 在棱1BB 上，且1AD EC ⊥，在棱BC 上是否存在点F ，满足//EF 平面1ADC ，若存在，求出BF 的值答案：存在，BF =证明：因为1AA ⊥面ABC ，故三棱柱111ABC A B C -为直三棱柱.故1AA ⊥面111A B C ，而1C D ⊂面111A B C ，故11AA C D ⊥，因为CA CB ==，故1111C A C B ==112B A =，因为D 是棱11A B 的中点，故111C D A B ⊥，因为1111AA A B A =， ∵直线1C D ⊥平面ADE ，而AD ⊂平面ADE ， ∵1C D AD ⊥，又1AD EC ⊥，111C D C E C ⋂=，∵AD ⊥平面1DEC ，而DE ⊂平面1DEC ，∵AD DE ⊥，在矩形11ABB A 中，11ADA DEB ∠=∠，11AA D DB E ∠=∠，故11ADA DEB ∠，故1111AA A D DB EB =11EB =即1=3EB ，故12BE EB =. 过E 作EG DE ⊥，交AB 于G ，取AB 的中点为L ，连接,DL CL ，则1DEB EGB ∠=∠，而190DB E EBG ∠=∠=︒，故1EBG DB E ， 所以11BG EB B E B D =31=，所以23BG =.在矩形11ABB A 中，因为11ADA DEB ∠=∠，故1ADA EGB ∠=∠，而1ADA DAL ∠=∠，所以EGB DAL ∠=∠，所以//AD EG ，而AD ⊂平面1ADC ，EG ⊄平面1ADC ，所以//EG 平面1ADC .在BC 上取点F ，使233BF BC ==，连GF ， 因为1BL =，故23BG BL =，故//GF CL . 在矩形11ABB A 中，因为,D L 为所在棱的中点，故11//,,DL AA DL AA =而1111//,,CC AA CC AA =故11//,CC DL CC DL =，故四边形1C DLC 为平行四边形，故1//DC CL ，故1//GF DC ，而1C D ⊂平面1ADC ，FG ⊄平面1ADC ，所以//FG 平面1ADC .因为GF EG G ⋂=，故平面以//EGF 平面1ADC ，因为EF ⊂平面EGF ，故//EF 平面1ADC .例3、如图，已知AD ⊥平面ABC ，EC ⊥平面ABC ，12AB AC AD BC ===，设P 是直线BE 上的点，当点P 在何位置时，直线//DP 平面ABC ？请说明理由证明：当点P 是BE 的中点时，//DP 平面ABC .理由如下：如下图，取BC 的中点O ，连接AO 、OP 、PD ，则//OP EC 且12OP EC =，因为AD ⊥平面ABC ，EC ⊥平面ABC ，所以//AD EC . 又12AD EC =，所以//OP AD 且OP AD =， 所以四边形AOPD 是平行四边形，所以//DP AO .因为AO ⊂平面ABC ，DP ⊄平面ABC ，所以//DP 平面ABC ；跟踪练习1、在三棱锥S ABC -中，AB ⊥平面SAC ，AS SC ⊥，1AB =，AC =，E 为AB 的中点，M 为CE 的中点，在线段SB 上是否存在一点N ，使//MN 平面SAC ？若存在，指出点N 的位置并给出证明，若不存在，说明理由证明：存在点N 为SB 上的靠近S 的四等分点即14SN SB =，//MN 平面SAC ， 证明如下：取AE 的中点F ，连接FN ，FM ，则//MF AC ，因为AC ⊂平面SAC ，MF ⊄平面SAC ，所以//MF 平面SAC ， 因为1124AF AE AB ==，14SN SB =， 所以FN //SA ，又SA ⊂平面SAC ，FN ⊄平面SAC ，所以//FN 平面SAC ，又MF FN F =，,MF FN ⊂平面MNF ，所以平面//MNF 平面SAC ，又MN ⊂平面MNF ，所以//MN 平面SAC ．2、在如图所示的五面体ABCDEF 中，∵ADF 是正三角形，四边形ABCD 为菱形，23ABC π∠=，EF //平面ABCD ，AB =2EF =2，点M 为BC 中点，在直线CD 上是否存在一点G ，使得平面EMG //平面BDF ，请说明理由证明：连接AC 交BD 于点O ，连接OM ，OF ，取CD 的中点G ，连接GM ，GE因为EF //平面ABCD ，EF ⊂平面ABEF ，平面ABEF ∩平面ABCD =AB ，所以EF //AB因为OM //AB //EF ，12OM AB EF ==，所以四边形OMEF 是平行四边形，所以OF //EM 因为EM ⊄平面BDF ，OF ⊂平面BDF ，所以EM //平面BDF因为点G 与点M 分别为CD 与BC 的中点，所以GM //BD因为GM ⊄平面BDF ，BD ⊂平面BDF ，所以GM //平面BDF而GM ∩EM =M ，平面EMG //平面BDF3、在长方体1111ABCD A B C D -中，已知AB AD =，E 为AD 的中点，）在线段11B C 上是否存在点F ，使得平面1//A AF 平面1ECC ？若存在，请加以证明，若不存在，请说明理由证明：存在，当点F 为线段11B C 的中点时，平面1//A AF 平面1ECC .证明：在长方体1111ABCD A B C D -中，11//AA CC ，11//AD B C .又因为1CC ⊂平面1ECC ，1AA ⊄平面1ECC ，所以1//AA 平面1ECC .又E 为AD 的中点，F 为11B C 的中点，所以1//AE FC ，且1AE FC =.故四边形1AEC F 为平行四边形，所以1//AF EC ，又因为1EC ⊂平面1ECC ，AF ⊄平面1ECC ，所以//AF 平面1ECC .又因为1AF AA A =，1AA ⊂平面1A AF ，AF ⊂平面1A AF ，所以平面1//A AF 平面1ECC .4、如图所示，在三棱柱ABC ﹣A 1B 1C 1中，平面ACC 1A 1∵平面ABC ，AA 1∵AC ，D ，D 1分别为AC ，A 1C 1的中点且AD =AA 1，在棱AA 1上找一点M ，使得1//D M 平面1DBC ，并说明理由答案：M 与A 重合时，1//D M 面1DBC ，理由见解析证明：当M 与A 重合时，D 1M ∵面DBC 1，理由如下：∵D 1C 1∵AD ，且D 1C 1=AD ，∵四边形D 1C 1DA 为平行四边形，∵D 1A ∵C 1D ，因为C 1D ∵面BDC 1，∵D 1M ∵面DBC 1.5、如图，在三棱锥P ABC -中，PA ⊥底面ABC ，ABC 是正三角形，E 是棱AB 的中点，如1AE =，在平面PAC 内寻找一点F 使得//BF 平面PEC ，并说明理由答案：答案见解析.证明：延长AC 至点G ，使得AC CG =，延长AP 至点H ，使得AP PH =，连接GH ，在直线GH 上任取一点F ，则点F 满足BF ∥平面PEC .理由如下： E 是线段AB 的中点，C 是线段AG 的中点，CE ∴是ABG 的中位线，∴BG CE ∥，BG ∴∥平面PEC .同理HG平面PEC ， 又BG HG G =，∴平面BHG平面PEC ， BF ⊂平面BHG ，BF ∴∥平面PEC .(注：若此题点F 直接取H 或G ，理由充分，给6分)6、已知四棱柱1111ABCD A B C D -的底面是边长为2的菱形，且BC BD =，1DD ⊥平面ABCD ，11AA =，BE CD ⊥于点E ，试问在线段11A B 上是否存在一点F ，使得//AF 平面1BEC ？若存在，求出点F 的位置；若不存在，请说明理由；证明：当F 为线段11A B 的中点时，//AF 平面1BEC .下面给出证明：取AB 的中点G ，连接EG ，1B G ，则1//FB AG ，且1FB AG =，所以四边形1AGB F 为平行四边形，所以1//AF B G .因为BC BD =，BE CD ⊥，所以E 为CD 的中点，又G 为AB 的中点，//AB CD ，AB CD =，所以//BG CE ，且BG CE =， 所以四边形BCEG 为平行四边形，所以//EG BC ，且EG BC =，又11//BC B C ，11BC B C =， 所以11//EG B C ，且11EG B C =，所以四边形11EGB C 为平行四边形， 所以11//B G C E ，所以1//AF C E ，又AF ⊄平面1BEC ，1C E ⊂平面1BEC ，所以//AF 平面1BEC ，7、在正三棱柱111ABC A B C -中，已知12,3AB AA ==，M ，N 分别为AB ，BC 的中点，P 为线段1CC 上一点．平面1ABC 与平面ANP 的交线为l ，是否存在点P 使得1//C M 平面ANP ？若存在，请指出点P 的位置并证明；若不存在，请说明理由证明：当2CP =时，1//C P 平面ANP证明如下：连接CM 交AN 于点G ，连接GP ，因为12CG CP GM PC ==，所以1//C M GP 又∵GP ⊂平面ANP ，1C M ⊄平面ANP ∵1C M 平面ANP。

空间中的平行一、知识梳理<一>线线平行与线面平行1.线线平行：定义：空间中两直线共面且没有交点，则两直线平行.证明两直线平行的主要方法是：①三角形中位线平行并等于底边的一半；②平行四边形两组对边分别平行；③梯形的一组对边平行；④直线平行的传递性：若a//b,b//c,则a//c.2.线面平行定义：若直线和平面没有交点，则称直线和平面平行.判定1：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行.（只需在平面内找一条直线和平面外的直线平行就可以）////a b a a b ααα⊄⎫⎪⊂⇒⎬⎪⎭判定2:两平面平行，一平面上的任一条直线与另一个平面平行.a a a a αβαββααβ⇒⇒⊂⊂⎫⎫⎬⎬⎭⎭或线面平行的性质：如果一条直线平行于一个平面，经过这条直线的平面与这个平面相交，那么这条直线和它们的交线平行.<二>面面平行1.定义：若两个平面没有交点，则两个平面平行2.判断：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行.,,a b a b A a b αααβββ⊂⊂⎫⎪=⇒⎬⎪⎭,,,a b a b A a a b b a b ααββ⊂⎫⎪=⎪⇒⎬''⎪⎪''⊂⎭判定定理的推论： 一个平面内的两条相交直线与另一个平面上的两条直线分别平行，两平面平行.3.两平面平行的性质： 性质Ⅰ：如果一个平面与两平行平面都相交，那么它们的交线平行.a ab b αβαγβγ=⇒=⎫⎪⎬⎪⎭性质Ⅱ：平行于同一平面的两平面平行；性质Ⅲ：夹在两平行平面间的平行线段相等；,,A C AC BD B D AB CD αβαβ∈⇒=∈⎫⎪⎪⎬⎪⎪⎭二、典例精析【例1】如图所示的几何体中，△ABC 是任意三角形，AE ∥CD ，且AE ＝AB ＝2a ，CD ＝a ，F 为BE 的中点．求证：DF ∥平面ABC .【练习】如图，已知P 是平行四边形ABCD 所在平面外一点，M 、N 分别是AB 、PC 的中点．求证：MN ∥平面P AD .【例2】已知正方形ABCD 所在的平面和正方形ABEF 所在的平面相交与AB ，M 、N 分别是AC 、BF 上的中点.求证：MN//平面BCE .【练习】如图，在四棱锥P-ABCD 中，底面ABCD 为矩形，E 为PD 的上一点，且PE=2ED ．若F 为PE 的中点.求证：BF ∥平面AEC .【例3】如图，四棱锥P-ABCD 中，底面ABCD 为梯形，AB ∥DC ，AB ⊥BC ．AB =BC=22AD ，点E 在棱PB 上，且PE=2EB ．求证：PD ∥平面EAC .【练习】如图，正四棱锥P-ABCD 中，PA=AB ，点M ，N 分别在PA ，BD 上，且31==BD BN PA PM .求证：MN ∥平面PBC .2【例4】a ，b ，c 为三条不重合的直线，α，β，γ为三个不重合平面，现给出六个命题①a ∥c ，b ∥c ⇒a ∥b ②a ∥γ ，b ∥γ ⇒a ∥b ③α∥c ，β∥c ⇒α∥β④ α∥γ ，β∥γ ⇒α∥β ⑤α∥c ，a ∥c ⇒α∥a ⑥α∥γ ，a ∥γ ⇒α∥a其中正确的命题是（ ）A.①②③⑥ B ．①④⑤ C ．①④ D ．①④⑥【练习】下面六个命题中正确命题的个数是（ ）①如果a 、b 是两条直线，b a //，那么a 平行于经过b 的任何一个平面；②如果直线a 和平面α满足a //α,那么a 与平面α内的任何一条直线平行；③如果直线a //α,b //α,那么b a //；④如果直线a 、b 和平面α满足b a //，a //α，α⊄b ，那么b //α；⑤如果直线a 与平面α上的无数条直线平行，则a //α；⑥如果平面α的同侧有两点A 、B 到平面α的距离相等，则AB //α.A. 0B. 1C. 2D. 3【例5】一条直线若同时平行于两个相交平面，那么这条直线与这两个平面的交线的位置关系是（ ）A ．异面B ．相交C ．平行D ．不能确定【练习】直线a //平面α，α内有n 条直线交于一点，这n 条直线直线中与直线a 平行的直线（ ）A.至少有一条 B ．至多有一条 C ．有且只有一条 D ．没有三、课后练习1．已知直线a ∥平面α，P α∈，那么过点P 且平行于α的直线（ ）A ．只有一条，不在平面α内B ．有无数条，不一定在α内C ．只有一条，且在平面α内D ．有无数条，一定在α内 2．若夹在两个平面间的三条平行线段相等，则这两个平面位置关系是（ ）A ．平行B ．相交C ．相交或平行D ．以上答案都不对3．下列结论中正确的是（ ） ①α∥β，β∥γ，则α∥γ；②过平面外一条直线有且只有一个平面与已知平面平行；③平面外的两条平行线中，如果有一条和平面平行，那么另一条也和这个平面平行；④如果一条直线与两个平行平面中一个相交，那么它与另一个必相交.A ．①②③B ．②③④C ．①③④D ．①②③④4．a ，b 是两条异面直线，A 是不在a ，b 上的点，则下列结论成立的是( )A ．过A 且平行于a 和b 的平面可能不存在B ．过A 有且只有一个平面平行于a 和bC ．过A 至少有一个平面平行于a 和bD ．过A 有无数个平面平行于a 和b5．如果平面α外有两点A 、B ，它们到平面α的距离都是a ，则直线AB 和平面α的位置关系是( )A ．平行B ．相交C ．平行或相交D ．AB ⊂α6.如图所示，在棱长为a 的正方体1111ABCD A BC D -中，E ，F ，P ，Q 分别是BC ，11C D ，1AD ，BD 的中点.(1)求证：PQ //平面11DCC D ；(2)在DC 上找一点H ，使EFH //平面11BB D D .7.如图，在空间四边形ABCD 中，P 、Q 分别是ABC ∆和BCD ∆的重心.求证：PQ ∥平面ACD .8.如图所示，已知三棱锥BCD A -被一平面所截，截面为平行四边形EFGH ，求证：（1）//EF 平面BCD ；（2）CD EF //.。

证明线线平行的方法：1.垂直于同一平面的两条直线平行2.平行于同一直线的两条直线平行3.一个平面与另外两个平行平面相交,那么2条交线也平行4.两条直线的方向向量共线,则两条直线平行5.线面平行的性质定理：一条直线和一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行。

证明线面平行的方法：1.直线与平面平行的判定性定理：如果不在一个平面内的一条直线和平面内的一条直线平行，那么这条直线和这个平面平行。

2.平面与平面平行的性质定理：如果两个平面是平行，那么在其中一个平面内的直线和另一个平面平行。

证明面面平行的方法：1.如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行。

2.面面平行的传递性：如果两个平面都和第三个平面平行，则这两个平面平行。

3.垂直与同一直线的两个平面平行。

4.利用向量法证明。

证明线线垂直的方法：1.定义法：两直线夹角90度2.三垂线定理：在平面内的一条直线，如果和穿过这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直3.直线与平面的定义：若1条直线垂直于一个平面，则它垂直于这个平面的所有直线4.法向量：在空间直角坐标系中，三点两向量确定一个平面，分别于这两个向量垂直的向量也就是分别与这两个向量乘积为0的向量垂直于这个平面，也就叫这个平面的法向量。

证明线面垂直的方法：1.直线垂直于平面内两条相交直线，则线与面垂直。

2.两条平行线一条垂直于平面，则另一条也垂直于这个平面。

3.如果两个面垂直，则其中一个面内垂直交线的线垂直另一个平面。

4.如果一条直线垂直于两个平行平面中的一个平面，那么它也垂直于另一个平面。

5.1来证。

6.证明面面垂直的方法：1.定义：两个平面相交，它们所成的二面角是直二面角。

2.如果一个平面经过另一个平面的一条垂线，那么这两个平面垂直。

12.设1A ，2A ，3A ，4A 是平面直角坐标系中两两不同的四点，若1312A A A A λ= (λ∈R)，1412A A A A μ=(μ∈R)，且112λμ+=,则称3A ，4A 调和分割1A ，2A ,已知点C(c ，o),D(d ，O) (c ，d∈R)调和分割点A(0，0)，B(1，0)，则下面说法正确的是(A)C 可能是线段AB 的中点(B)D 可能是线段AB 的中点(C)C ，D 可能同时在线段AB 上(D) C ，D 不可能同时在线段AB 的延长线上【答案】D【解析】由1312A A A A λ= (λ∈R)，1412A A A A μ=(μ∈R)知:四点1A ，2A ，3A ，4A 在同一条直线上,因为C,D 调和分割点A,B,所以A,B,C,D 四点在同一直线上,且112c d+=, 故选D. 如图，在四棱台1111ABCD A B C D -中，1D D ⊥平面ABCD ，底面ABCD 是平行四边形，AB=2AD ，11AD=A B ，BAD=∠60°（Ⅰ）证明：1AA BD ⊥；（Ⅱ）证明：11CC A BD ∥平面.【解析】（Ⅰ）证明：因为AB=2AD ，所以设AD=a,则AB=2a,又因为BAD=∠60°,所以在ABD ∆中,由余弦定理得：2222(2)22cos 603BD a a a a a =+-⨯⨯=,所以BD=3a ,所以222AD BD AB +=,故BD ⊥AD,又因为1D D ⊥平面ABCD ，所以1D D ⊥BD,又因为1AD D D D ⋂=, 所以BD ⊥平面11ADD A ,故1AA BD ⊥.(2)连结AC,设AC ⋂BD=0, 连结1A O ,由底面ABCD 是平行四边形得:O 是AC 的中点,由四棱台1111ABCD A B C D -知:平面ABCD ∥平面1111A B C D ,因为这两个平面同时都和平面11ACA C 相交,交线分别为AC 、11A C ，故11AC AC ，又因为AB=2a,BC=a, ABC=120∠，所以可由余弦定理计算得，又因为A 1B 1=2a, B 1C 1=2a , 111A B C =120∠，所以可由余弦定理计算得A 1C 1=2a ，所以A 1C 1∥OC 且A 1C 1=OC ，故四边形OCC 1A 1是平行四边形，所以CC 1∥A 1O ，又CC 1⊄平面A 1BD ，A 1O ⊂平面A 1BD ，所以11CC A BD ∥平面.20.（本小题满分12分）等比数列{}n a 中，123,,a a a 分别是下表第一、二、三行中的某一个数，且123,,a a a 中的任何两个数不在下表的同一列.（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）若数列{}n b 满足：(1)ln n n n b a a =+-，求数列{}n b 的前2n 项和2n S .【解析】（Ⅰ）由题意知1232,6,18a a a ===,因为{}n a 是等比数列,所以公比为3,所以数列{}n a 的通项公式123n n a -=⋅.（Ⅱ）因为(1)ln n n n b a a =+-=123n -⋅+1(1)ln 23n --⋅, 所以12n n S b b b =+++=1212()(ln ln ln )n n a a a a a a +++-++=2(13)13n ---12ln n a a a =31n --121ln(21333)n n -⋅⨯⨯⨯⨯= 31n --(1)2ln(23)n n n -⋅,所以2n S =231n --2(21)22ln(23)n n n -⋅=91n --22ln 2(2)ln 3n n n --.15.（本小题满分14分）在平面直角坐标系xOy 中，点A(－1,－2)、B(2,3)、C(－2,－1).（1）求以线段AB 、AC 为邻边的平行四边形两条对角线的长；（2）设实数t 满足(OC t AB -)·OC =0，求t 的值.16. （本小题满分14分）如图，在四棱锥P-ABCD 中，PD ⊥平面ABCD ，PD=DC=BC=1，AB=2，AB ∥DC ，∠BCD=900.（1）求证：PC ⊥BC ；（2）求点A 到平面PBC 的距离.19.（本小题满分16分）设各项均为正数的数列{}n a 的前n 项和为n S ，已知3122a a a +=，数列{}nS 是公差为d 的等差数列.（1）求数列{}n a 的通项公式（用d n ,表示）（2）设c 为实数，对满足n m k n m ≠=+且3的任意正整数k n m ,,，不等式k n m cS S S >+都成立，求证：c 的最大值为29.10、已知→→21,e e 是夹角为π32的两个单位向量，,,22121→→→→→→+=-=e e k b e e a 若0=⋅→→b a ，则k 的值为13、设7211a a a ≤≤≤≤ ，其中7531,,,a a a a 成公比为q 的等比数列，642,,a a a 成公差为1的等差数列，则q 的最小值是________16、如图，在四棱锥ABCD P -中，平面PAD ⊥平面ABCD ，AB=AD ，∠BAD=60°，E 、F 分别是AP 、AD 的中点求证：（1）直线E F ‖平面PCD ；（2）平面BEF ⊥平面PAD20、设M 为部分正整数组成的集合，数列}{n a 的首项11=a ，前n 项和为n S ，已知对任意整数k 属于M ，当n>k 时，)(2k n k n k n S S S S +=+-+都成立（1）设M=｛1｝，22=a ，求5a 的值；（2）设M=｛3，4｝，求数列}{n a 的通项公式 1. F E A D如图，在长方体1111ABCD A B C D -中，3AB AD cm ==，12AA cm =，则四棱锥11A BB D D -的体积为 ▲ 3cm ． 答案：62. 在平面直角坐标系xOy 中，若双曲线22214x y m m -=+的离心率为5，则m 的值为 ▲ ．答案：23. 如图，在矩形ABCD 中，2AB =，2BC =，点E 为BC 的中点，点F 在边CD 上，若2AB AF =，则AE BF 的值是 ▲ ．答案：24. （本小题满分14分）在ABC ∆中，已知3AB AC BA BC =．A B C E F D （第7题）（1） 求证：tan 3tan B A =；（2） 若cos C =求A 的值． 解：（1）∵3AB AC BA BC = ∴3AB AC cos A BA BC cos B = ∴3AC cos A BC cos B = 由正弦定理得：AC BC sin B sin A =∴3sin B cos A sin A cos B =∴3tan B tan A =（2）∵cos C =0C π<<∴5sinC = ∴2tanC = ∴()2tan A B +=-又∵3tan B tan A =∴23421113tan A tan B tan A tan A tan A tan Atan B tan A tan B tan A++-===--- ∴1tan A =或13- ∵3tan B tan A =∴A ，B 必为锐角，否则A ，B 同时为钝角，这与三角形的内角和小于180矛盾 ∴0tan A >∴1tan A =∴4A π=5. （本小题满分14分）如图，在直三棱柱111ABC A B C -中，1111A B AC =，D E ，分别是棱1BC CC ，上的点（点D 不同于点C ），且AD DE F ⊥，为11B C 的中点． 求证：（1） 平面ADE ⊥平面11BCC B ；（2） 直线1//A F 平面ADE ．证明：（1）∵三棱柱111ABC A B C -是直三棱柱 ∴1CC ABC ⊥平面∵AD ABC ⊂平面∴1CC AD ⊥∵AD DE ⊥，且1DE CC E = ∴11AD BCC B ⊥平面∵AD ABC ⊂平面∴11ADE BCC B ⊥平面平面（2）∵11AD BCC B ⊥平面， 11BC BCC B ⊂平面∴AD BC ⊥∵直三棱柱111ABC A B C -中，1111A B AC = ∴AB AC =∴D 是BC 的中点∵F 是11B C 的中点 ∴1DFAA ，且1DF AA =∴四边形1AA FD 是平行四边形 ∴1A FAD∵1D F A A E ⊄平面，1D F A A E ⊂平面 ∴1//A F 平面ADE 6. （本小题满分16分）已知各项均为正数的两个数列{}n a 和{}n b 满足：122n n n n n a n a b *+=∈+N ．（1） 设11n n nb b n a *+=+∈N ，，求证：数列2nn b a ⎧⎫⎛⎫⎪⎪⎨⎬ ⎪⎝⎭⎪⎪⎩⎭是等差数列；（2） 设12nn nb b n a *+=∈N ，，且{}n a 是等比数列，求1a 和1b 的值． 解： （1）∵()22222221221211n n n n*n n n n n n n n n nnn n a b a b bb b a b b n N a a b a a a ++⎛⎫+ ⎪⎛⎫⎛⎫⎛⎫⎛⎫⎪-=-=-=∈ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎪ ⎪⎝++⎭+ （2）∵0n a >，0n b >∴()()22222n n n n n n a b a b a b +≤+<+∴12212n n n n na ab +<=≤+∵{}n a 是各项都为正数的等比数列 ∴设其公比为q ，则0q >①当1q >时， ∵0n a >∴数列{}n a是单调递增的数列，必定存在一个自然数，使得1n a +> ②当01q <<时 ∵0n a >∴数列{}n a 是单调递减的数列，必定存在一个自然数，使得11n a +< 由①②得：1q = ∴()1*n a a n N =∈∵11n a +<=≤得：1a =，且11a <≤∴1n b =∵*11n n n n b b n N a +==∈， ∴数列{}n b是公比为1a 的等比数列∵11a <≤∴11a ≥ ①当11a >时 数列{}n b是单调递增的数列，这与1n b =矛盾 ②11=时数列{}n b 是常数数列，符合题意∴1a∴n b∴1b =1.如图，在三棱柱ABC C B A -111中，F E D ,,分别是1,,AA AC AB 的中点，设三棱锥ADE F -的体积为1V ，三棱柱ABC C B A -111的体积为2V ，则=21:V V ▲ .解析：112211111334224ADE ABC V S h S h V ==⨯⨯=所以121:24V V =2.3. 设E D ,分别是ABC ∆的边BC AB ,上的点，AB AD 21=,BC BE 32=,若AC AB DE 21λλ+=(21,λλ为实数)，则21λλ+的值为 ▲ .解析： 易知()121212232363DE AB BC AB AC AB AB AC =+=+-=-+ 所以1212λλ+=4.在正项等比数列{}n a 中，215=a ，376=+a a .则满足n n a a a a a a a a ......321321>++++的最大正整数n 的值为 ▲ . 解析：ABC1ADE F1B1C2252552667123123115521155223 (1),.222222011522360022n n n n n n n n n n a a a a a a a a a a q a q q a a n nq n q n q a -------=+=+-+=∴++++>∴->∴->>-∴-><<=>∴==n N +∈112,n n N +∴≤≤∈又12n =时符合题意，所以n 的最大值为12 15.（本小题满分14分）已知()cos sin a αα=，，()cos sin b ββ=，，0βαπ<<<. (1) 若2a b -=，求证：a b ⊥；(2) 设()01c ,=，若a b c +=，求α，β的值.解：(1)()()cos ,sin ,cos ,sin ,0a b ααβββαπ==<<<2a b -= 22a b ∴-=2222a b ab ∴+-= 1122a b +-⋅= 0a b ⋅= a b ∴⊥ (2)()()()0,1,cos cos ,sin sin 0,1cos cos 0sin sin 1c a b cαβαβαβαβ=+=∴++=∴+=∴+=①②22+①②得：()2+2cos 1αβ-= ()1cos 2αβ-=-0023βαπαβππαβ<<<∴<-<∴-=又cos cos 05,66αβαβπππαβ+=∴+=∴==16. （本小题满分14分）如图，在三棱锥S ABC -中，平面SAB ⊥平面SBC ，AB BC ⊥,AS AB =. 过A 作AF SB ⊥，垂足为F ，点E ,G 分别是侧棱SA ,SC 的中点.求证：(1) 平面EFG //平面ABC ; (2) BC SA ⊥. 解：(1),E G 分别是侧棱,SA SC 的中点EG AC ∴∥AC 在平面ABC 中，EG 在平面外EG ∴∥平面ABC,AS AB AF SB =⊥F ∴为SB 中点 EF AB ∴∥AB 在平面ABC 中，EF 在平面外EF ∴∥平面ABCEF 与EG 相交于E,EF EG 在平面EFG 中 ∴ 平面EFG //平面ABC(2)平面SAB ⊥平面SBCSB 为交线AF 在SAB 中，AF SB ⊥AF ∴⊥平面SBC AF BC ∴⊥BC AB ⊥AF 与AB 相交于A ,AF AB 在平面SAB 中 BC ∴⊥平面SAB BC SA ∴⊥ 19. （本小题满分16分）设{}n a 是首项为a ，公差为d 的等差数列()0d ≠，n S 是其前n 项和. 记2nn nS b n c=+，N n *∈，其中c 为实数.(1) 若0c =，且1b ，2b ，4b 成等比数列，证明：()2N nk k S n S k,n *=∈； (2) 若{}n b 是等差数列，证明：0c =. 解：（1）()()10n a a n d d =+-≠22n n nS na d -=+ 0c =时，nn S b n=112244122342S b a S db a S d b a ====+==+124,,b b b 成等比2142b b b ∴=222222222322202n nk k nk kd d a a a d ad d d aS n a S n k a n S n k a S n S ⎛⎫⎛⎫∴⋅+=+ ⎪ ⎪⎝⎭⎝⎭∴=≠∴=∴===∴=（2）由已知23222222n n nS n a n d n db nc n c+-==++n b 是等差数列∴设n b kn b =+（k,b 为常数）∴有()()32222220k d n b d a n ckn bc -++-++=对任意n N +∈恒成立202202020k d b d a ck bc -=⎧⎪+-=⎪∴⎨=⎪⎪=⎩0d ≠k c ∴≠∴=此时222dka d b=-=命题得证3.。