配合物的晶体场理论和配位场理论

第三章配合物的化学键理论目标：解释性质，如配位数、几何结构、磁学性质、光谱、热力学稳定性、动力学反应性等。

三种理论：①价键理论、②晶体场理论、③分子轨道理论第一节价键理论（Valence bond theory）由L.Pauling提出要点：①配体的孤对电子可以进入中心原子的空轨道；②中心原子用于成键的轨道是杂化轨道（用于说明构型）。

一、轨道杂化及对配合物构型的解释能量相差不大的原子轨道可通过线性组合构成相同数目的杂化轨道。

对构型的解释（依据电子云最大重叠原理：杂化轨道极大值应指向配体）二、AB n型分子的杂化轨道1、原子轨道的变换性质考虑原子轨道波函数，在AB n分子所属点群的各种对称操作下的变换性质。

类型轨道多项式sp x xp p y yp z zd xy xyd xz xzd d yz yzd x2-y2x2-y2d z22z2-x2-y2（简记为z2）*s轨道总是按全对称表示变换的。

例：[HgI3]- (D3h群)平面三角形A1′：d z2、sE′：(p x、p y )、(d x2-y2、d xy)A2″：p zE″：(d xz、d yz)2、σ轨道杂化方案1）四面体分子AB4（Td）[CoCl4]2-以四个杂化轨道的集合作为分子点群(Td)表示的基，确定该表示的特征标：E 2 -1 2 0 0 (z2, x2-y2)T1 3 0 -1 1 -1T2 3 0 -1 -1 1 (xy,xz,yz) (x,y,z)a(A1)=1/24(1×4+8×1×1+3×1×0+6×1×0+6×1×2)=1a(A2)=1/24 [1×4+8×1×1+3×1×0+6×(-1)×0+ 6×(-1)×2]=0a(E)=1/24 [2×4+8×(-1)×1+3×2×0+6×0×0+ 6×0×2]=0a(T1)=1/24 [3×4+8×0×1+3×(-1)×0+6×1×0+6×(-1)×2]=0a(T2)=1/24 [3×4+8×0×1+3×(-1)×0+6×(-1)×0 +6×1×2]=1约化结果Γ=A1+T2由特征标表：A1T2s (p x、p y、p z)(d xy、d xz、d yz)可有两种组合：sp3（s、p x、p y、p z）、sd3（s、d xy、d xz、d yz)* 以一组杂化轨道为基的表示的特征标的简化计算规则：Γ 5 2 1 3 0 3约化结果：Γ= 2A1′+A2〞+E′A1′A2〞E′s p z (p x、p y)d z2(d xy、d x2-y2)两种可能的组合：（s、d z2、p z 、p x、p y）( s、d z2、p z、d xy、d x2-y2)约化得：Γ=A1g+B1g+E uA1g B1g E us d x2-y2(p x、p y)d z2两种类型：dsp2（d x2-y2、s、p x、p y）、d2p2（d z2、d x2-y2、p x、p y）5）八面体AB6(O h) 例：[Fe(H2O)6]3+（d z2、d x2-y2、s、p x、p y、p z) 3、π成键杂化方案在AB n分子中，原子A上要有2n个π型杂化轨道和在B原子上的2n个π原子轨道成键。

配位化学讲义第四章（1）价键理论、晶体场理论第三章配合物的化学键理论目标：解释性质，如配位数、几何结构、磁学性质、光谱、热力学稳定性、动力学反应性等。

三种理论：①价键理论、②晶体场理论、③分子轨道理论第一节价键理论（Valencebond theory）由L.Pauling提出要点：①配体的孤对电子可以进入中心原子的空轨道；②中心原子用于成键的轨道是杂化轨道（用于说明构型）。

一、轨道杂化及对配合物构型的解释能量相差不大的原子轨道可通过线性组合构成相同数目的杂化轨道。

对构型的解释（依据电子云最大重叠原理：杂化轨道极大值应指向配体）指向实例sp3、sd3杂化四面体顶点Ni(CO)4sp2、sd2、dp2、d3杂化三角形顶点[AgCl3]2-dsp2、d2p2 杂化正方形顶点[PtCl4]2-d2sp3杂化八面体顶点[Fe(CN)6]4-sp杂化直线型[AgCl2]-二、AB n型分子的杂化轨道1、原子轨道的变换性质考虑原子轨道波函数，在AB n分子所属点群的各种对称操作下的变换性质。

类型轨道多项式sp x xp p y yp z zd xy xyd xz xzd d yz yzd x2-y2x2-y2d z22z2-x2-y2（简记为z2）*s轨道总是按全对称表示变换的。

例：[HgI3]- (D3h群)平面三角形A1′：d z2、sE′：(p x、p y )、(d x2-y2、d xy)A 2″：p zE″：(d xz、d yz)2、σ轨道杂化方案1）四面体分子AB4（Td）[CoCl4]2-以四个杂化轨道的集合作为分子点群(Td)表示的基，确定该表示的特征标：r1r4r2r3恒等操作，χ(E)=4 C3操作，χ(C3)=1对C2、S4和σd用同样方法处理，得T d E 8C3 3C2 6S46σdΓ 4 1 00 2约化：T d E 8C3 3C2 6S4 6σdA1 1 1 1 11A2 1 1 1 -1 - 1E 2 -1 2 00 (z2, x2-y2)T1 3 0 -1 1 -1T2 3 0 -1 -11 (xy,xz,yz) (x,y,z)a(A1)=1/24(1×4+8×1×1+3×1×0+6×1×0+6×1×2)=1a(A2)=1/24 [1×4+8×1×1+3×1×0+6×(-1)×0+6×(-1)×2]=0a(E)=1/24 [2×4+8×(-1)×1+3×2×0+6×0×0+6×0×2]=0a(T1)=1/24 [3×4+8×0×1+3×(-1)×0+6×1×0+6×(-1)×2]=0a(T2)=1/24 [3×4+8×0×1+3×(-1)×0+6×(-1)×0+6×1×2]=1约化结果Γ=A1+T2由特征标表：A1T2s(p x、p y、p z)(d xy、d xz、d yz)可有两种组合：sp3（s、p x、p y、p z）、sd3（s、d xy、d xz、d yz)* 以一组杂化轨道为基的表示的特征标的简化计算规则：①不变（1）②改变符号（-1）③与其他函数变换（0）2）再以[CdCI5]3-三角双锥(D3h)为例：41325D3h E 2C33C2σh2S3 3σvΓ 5 2 13 0 3约化结果：Γ= 2A1′+A2〞+E′A1′A2〞E′s p z (p x、p y)d z2(d xy、d x2-y2)两种可能的组合：（s、d z2、p z 、p x、p y）( s、d z2、p z、d xy、d x2-y2)3）[HgI3]- ( D3h)123D3h E 2C3 3C2σh2S33σvΓ 3 0 13 0 1约化得：Γ=A1′+E′A1′E′s (p x、p y)d z2(d xy、d x2-y2)可能的组合有：（s、p x、p y）、(s、d xy、d x2-y2)、(d z2、p x、p y)、(d z2、d xy、d x2-y2)4）平面AB4型分子（D4h）例：[PtCl4]2-C2′C2″D4h E 2C4(C41,C43) C2(C42) 2C2′2C2″i 2S4σh 2σv2σdΓ 4 0 0 20 0 0 4 2 0约化得：Γ=A1g+B1g+E uA1g B1g E us d x2-y2(p x、p y)d z2两种类型：dsp2（d x2-y2、s、p x、p y）、d2p2（d z2、d x2-y2、p x、p y）5）八面体AB6(O h) 例：[Fe(H2O)6]3+O h E 8C3 6C26C4 3C2i 6S4′8S6 3σh 6σdΓ 6 0 0 2 2 0 0 0 4 2约化得：Γ=A1g+E g+T1u A1g E gT1us (d z2、d x2-y2) (p x、p y、p z)只有唯一的d2sp3杂化（d z2、d x2-y2、s、p x、p y、p z)3、π成键杂化方案在AB n分子中，原子A上要有2n个π型杂化轨道和在B原子上的2n个π原子轨道成键。

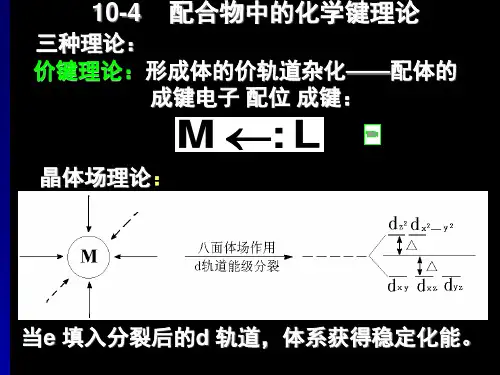
配位场理论
有三种理论用于说明和解释配合物的结构和性能：价键理论、晶体场理论和分子轨道理论。

30年代初，鲍林将价键理论应用于配合物结构，能够解释一些
问题，但有些问题不能解释。

到50年代，引入晶体场理论和分子轨
道理论解释配合物中的化学结合和化学结构，形成了配位场理论。

配位场理论是晶体场理论的发展，其实质是配位化合物的分子轨道理论。

配位场理论在处理中心金属原子在其周围配体所产生的场作用下，金属原子轨道能级发生变化时，以分子理论轨道方法为主，采用类似的原子轨道线性组合等数学方法，根据配体场的对称性进行简化，并吸收晶体场理论的成果，阐明配位化合物的结构和性质。

在配位场理论中，中心离子的d轨道分裂及能级变化与晶体场相同。

在有些配合物中，中心离子（通常也称中心原子）周围被按照一定对称性分布的配位体所包围而形成一个结构单元。

配位场就是配位体对中心离子（这里大多是指过渡金属络合物）作用的静电势场。

由于配位体有各种对称性排布，遂有各种类型的配位场，如四面体配位化合物形成的四面体场，八面体配位化合物形成的八面体场等。

随着无机和有机配合物合成的日益增多和各种结构与性能的研究，配位场理论不断发展，成为近代重要的化学键理论之一，是理论物理和理论化学的一个重要分支。

它在解释配位化合物的结构与性能关系、催化反应机理，激光物质的工作原理以及晶体的物理性质等方面都得到广泛的应用。

晶体场理论与分子轨道理论的比较及配位场理论黄珺(湖北师范学院化学与环境工程系0303班，湖北黄石，435002)摘要：配位化合物中的化学键主要是指中心离子和配位体之间的化学键。

自1893年维尔纳提出了配位理论后，有关配合物中的化学键理论主要有现代价键理论、晶体场理论、配位键理论和分子轨道理论。

本文主要讨论分子轨道理论和晶体场理论。

分子轨道理论以量子力学为基础，用于说明共价分子结构。

晶体场理论是1929年由皮赛和范弗雷克提出的，用于配合物化学键研究，成功地解释了配合物的磁性、光学性质及结构等，故在配合物的化学键理论中确立了重要地位。

关键词：晶体场理论、分子轨道理论、配位场理论、配位键、化学键Crystal field theory and molecular orbit theory comparison and legend field theoryHuang Jun(Chemistry and environment engineering department, Hubei Normal University, Huangshi, 435002)Abstract:In the coordination compound chemical bond mainly was refers to between the central ion and the legend chemical bond .The Vyell natrium proposed since 1893 the coordinate theory ,in the related preparation chemical bond theory mainly had the present price key theory and the crystal field theory ,the coordination bond theory and the molecular orbit theory .This article main discussion molecular orbit theory and the crystal field theory .Molecular orbit theory take the quantum mechanics as a foundation ,used in explaining the covalent molecule structure .The crystal field theory was in 1929 proposes by H.Bathe and J.H.Van Vleck ,used in the preparation chemical bond research ,successfully explained and preparation magnetism ,the optical quality and the structure and so on ,therefore has established the important status in the preparation chemical bond theory. Key words: Crystal field theory molecular orbital theory legend field theory coordinate bond chemical bond晶体场理论是20世纪50年代初,在价键理论和纯静电理论的基础上发展起来的.晶体场理论把中心离子看作是带正电的点电荷,把配位体看作是带负电的点电荷,它们之间的结合完全看作是静电和排斥作用.同时考虑到配位体对中心离子d轨道的影响,它在解释光学和磁学等性质方面很成功.（分子轨道理论把组成分子的所有原子作为一个分子整体来考虑,在分子中的电子不再从属于某些特定的原子,而是遍及整个分子范围内运动,分子中每个电子运动状态,可以用波函数来描述.）[1]首先,来比较这两种理论的基本观点.晶体场理论的基本观点:(1) 在配合物中,中心离子和配位体之间的相互作用类似于离子晶体中正、负离子间的静电作用,故它们间的化学键力纯属静电作用力.(2)当中心离子(指d区元素的离子)处于由配体所形成的非球形对称的负电场中时,中心离子的d 电子将受到配体负电场的排斥作用,使5个等价的d轨道发生能级分裂,有些轨道的能量降低.(3)中心离子的d轨道产生能级分裂后,致使中心离子的d电子排布也发生变化,导致体系的能量变化.（分子轨道理论的基本观点是把分子作为一个整体加以考虑,而分子中的每个电子是这个整体中的一员,不再从属于原来所属的原子.第一,原子形成分子后,电子就不再局限于个别原子的原子轨道,而是从属于整个分子的分子轨道,所以分子轨道强调分子的整体性.第二,分子轨道中电子的分布也和原子中的电子分布一样,遵循保里不相容原理,能量最低原理和洪特规则,在分子轨道中电子可以配对,也可以不配对.第三,分子轨道中可以近似地通过原子轨道的适当组合而得到,分子轨道的数目等于组合前原子轨道数目之和,原子轨道在组合成分子轨道时,要符合分子对称原则,最大重叠原则和能量相近原则,才能形成有效的分子轨道.）[3]研究络合物结构就是研究络合物中配位体与中央金属之间的化学键.晶体场理论把M—L作用看作是不同对称性，正、负离子的静电作用，完全不考虑共价键的因素。

.配位化合物的价键理论配合物的晶体场理论一.配合物的构型与中心的杂化方式二中心杂化轨道的形成1. ns np nd 杂化1 个 4s 空轨道，3 个 4p 空轨道和2 个 4d 空轨道形成 sp3d2杂化轨道，正八面体分布。

6 个F-的 6 对孤对电子配入sp3d2空轨道中，形成正八面体构型的配合单元。

例 2 Ni(CO)4的成键情况在配体 CO 的作用下，Ni 的价层电子重排成 3d104s0形成 sp3杂化轨道，正四面体分布，4 个CO 配体与 sp3杂化轨道成配键，形成的 Ni(CO)4构型为正四面体。

例 1 和例 2 的相同点是，配体的孤对电子配入中心的外层空轨道, 即 ns np nd 杂化轨道, 形成的配合物称外轨型配合物. 所成的键称为电价配键. 电价配键不是很强.例 1 和例 2 的不同点是，CO 配体使中心的价电子发生重排，这样的配体称为强配体。

常见的强配体有 CO、 CN-、NO2-等；例1 中 F-不能使中心的价电子重排，称为弱配体。

常见的弱配体有 F-、Cl-、H2O 等。

而 NH3等则为中等强度配体。

对于不同的中心，相同的配体其强度也是不同的。

2. (n-1) d ns np 杂化例 3 讨论的成键情况形成 d2sp3杂化，使用 2 个 3d 轨道, 1 个 4s 轨道，3个4p 轨道。

用的内层 d 轨道。

形成的配离子为正八面体构型。

空出 1 个内层 d 轨道，形成 dsp2杂化轨道，呈正方形分布。

故构型为正方形。

例 3 和例 4 中，杂化轨道均用到了 ( n - 1 ) d 内层轨道，配体的孤对电子进入内层，能量低，称为内轨配合物，较外轨配合物稳定。

所成的配位键称为共价配键。

三价键理论中的能量问题内轨配合物稳定，说明其键能 E内大，大于外轨的 E外，那么怎样解释有时要形成外轨配合物呢？其能量因素如何？上面的例题中我们看到，形成内轨配合物时发生电子重排，使原来平行自旋的 d 电子进入成对状态，违反洪特规则，能量升高。

第九讲：多原子分子金属配合物晶体场理论1. 金属配合物2MLn: 金属离子或原子与它周围n 个离子或分子形成的化合物价键理论（VB）例如[Fe( H2O )6]3+配合物的中央离子(或原子)和配位体之间的化学键可分为电价配键和共价配键两种。

电价配合物，带正电的中心离子和带负电或具有偶极矩的配位体之间是靠静电引力结合成键，呈高自旋状态。

共价配合物，配位体的孤对电子和中心离子空的杂化价轨道形成共价配键，呈低自旋状态。

价键理论说明了高自旋配合物和低自旋配合物产生的原因，对配合物的磁性和几何构型也都给予了一定的说明。

但作为一个定性的理论，价键理论有很大的局限性。

1). 历史3晶体场（CFT）分子轨道法（MO）1929年，H.Bethe 用量子力学结合群论初步建立了晶体场方法。

将配合物视为一个大的分子，用MO法处理。

因包含金属d 轨道，MO成分较为复杂。

在MO法中，对称性匹配原则是关键因素。

1950年代以后，人们吸收上述理论的优点，发展了配位场理论。

1932年，van Vleck 在Bethe的工作基础上，提出过渡金属配合物的化学键理论，较好地解释金属配合物的磁性和稳定性。

1. 金属配合物5.3 金属配合物晶体场理论2. 晶体场理论1)、基本思想金属配合物的成键类似于离子晶体中正负离子的作用。

（i）金属与配体的作用为静电作用，配体视为点电荷。

（i i）配体的作用是建立一个负电荷势场（晶体场），在晶体场的微扰下，金属的d轨道发生能级分裂。

（i i i）金属的电子从低到高填充分裂后的d轨道，使总能量下降，产生附加成键效应。

分裂后总能量的下降称晶体场稳定化能（CFSE）。

42. 晶体场理论8（ii）d轨道分裂模式：由晶体场的对称性决定。

中心力场O h 的不可约表示对于正八面体场，5个d轨道按O h 群的不可约表示分类（查特征标表或相关表）原来简并的d 轨道分裂为两组：e g 和t 2g 。

gz y x gzx yz xy e d d t d d d ⎪⎭⎪⎬⎫⎪⎭⎪⎬⎫-22222. 晶体场理论10两组能级的高低（直观观察）ge 2gt ∆:∆分裂能2. 晶体场理论14（i）用群论知识了解d轨道分裂为几组。