运筹学上机攻略
- 格式:doc
- 大小:117.50 KB
- 文档页数:3
运筹学上机攻略一、规划求解的预备知识1、打开Excel软件的工具→→加载宏→→规划求解(选定),单击确定;加载宏成功后,关闭再重新打开excel。
注明:这个宏是office自带的,一般情况下不启用的哦,所以要加载。
2、如果上述方法,不能成功加载成功,请到网上下载规划求解宏solver.xla。
二、规划求解的操作步骤1、首先将已经建立好的书面数学模型,按照Excel的输入规定,将逻辑公式输入到打开的工作薄文件的一个电子表格中;2、然后,打开“工具”→→“规划求解”,出现“规划求解参数”对话框;例:(1)在“设置目标单元格”中输入规划模型的目标函数所在的引用位置(可以手动输入、也可采用捷径操作方法:将鼠标光标放在“设置目标单元格”里,再用鼠标点击“Excel中的目标区“);(2)选择目标的优化方向,即确定最大值、最小值,还是需要输入特定值;(3)在“可变单元格”中输入每个变量的引用位置或名称(也可采用捷径操作);(4)鼠标点击“添加”、修改或删除,打开下一级对话框,开始对规划模型的约束对话,并在输入完毕后还回“规划求解参数”主对话框。
例:(注意:单元格引用位置也可以采用捷径操作)、约束值手动输入。
(5)鼠标点击“选项”,打开下一级对话框,开始规划模型的选项对话,并在输入完毕后还回“规划求解参数”主对话框。
3、以上工作完毕后,点击“求解”。
三、例子变量:甲的产量X1,乙的产量X2目标函数:maxZ(X1,X2)=4X1+5X2约束条件:X1+X2≤452X1+X2≤80X1+3X2≤90X1,X2≥0第一步:在EXCEl中,输入逻辑公式,如下图:第二步:打开“工具”→→“规划求解”,按步骤2的1-4步操作,出现下图:【引用位置($C$6、$C$9、$C$10)等,可以手动输入、也可采用捷径操作方法:将鼠标光标放在“设置目标单元格”里,再用鼠标点击“Excel中的目标区“)】第三步:求解结果:Microsoft Excel 11.0 运算结果报告工作表 [Book1]Sheet1报告的建立: 2011-9-16 17:29:14目标单元格 (最大值)单元格名字初值终值$C$6 目标函数0 202.5可变单元格单元格名字初值终值$C$9 决策变量X1 0 22.5$C$10 决策变量X2 0 22.5约束单元格名字单元格值公式状态型数值$C$12 约束A 45 $C$12<=45 到达限制值$C$13 约束B 67.5 $C$13<=80 未到限制值12.5$C$14 约束C 90 $C$14<=90 到达限制值$C$15 甲产量22.5 $C$15>=0 未到限制值22.5$C$16 乙产量22.5 $C$16>=0 未到限制值22.5。

. 1实验报告实验课程名称运筹学实验工程名称大M法或两阶段法的上机实验年级专业学生学号00 学院实验时间:年月日实验容〔包括实验具体容、算法分析、源代码等等〕:1.书上P97页第6题:用大M 法和两阶段法求解以下线性规划问题。
ma* z=5;3213x x x ++ 约束条件:102x 4x x 321≥++,16.x 2x -x 321≤+A :大M 法图1.1图1.2δ,得出目标函数的最优解*1=16,*2=0,由上面的结果可知,满足所求出的0≤j*3=0,s*4=16,R*5=0,s*=0,最优值是80。
当把M的值改为100000后,值还是一样的,这样就可以得出当M为100时,已经得出有效解。
B:两阶段法图1.3由图1.3可知,先进展线性规划的第一阶段,满足0≤j δ,且z 值为零,即说明存在一个可行解使得所有的人工变量都为零,此时*2=2.5,s*6=21,其余为0得出z=0。
接下来进展第二阶段,令z=5*1+*2+3*3-0s*4+0R*5+0s*6,和大M 的分析方法一样,最终将得到满足0≤j δ时到达最优解:当*1=16,*2=0,*3=0,s*4=6,R*5=0,s*6=0,最优值为80。
2.书上P97页第7题〔4〕大M 法和两阶段法求解以下线性规划问题 。
ma* z=;321x x 2x ++ 约束条件:,42x 2x 4x 321≥++,204x 2x 21≤+,162x 8x 4x 321≤++ A :大M 法图2.1图2.2由上面的图 2.1可知,首先先输入数据即线性规划的系数如图 2.1所示令ma* z=321x x 2x ++-0s*4+0s*6+0s*7-MR*5;进展下一次迭代,以同样的方法一直下去,直到所求出的为止0≤j δ,就可以得出目标函数的最优解:*1=4,s*4=12,s*6=12,其余为0时,最优值为8。
当把M 的值改为100000后,值还是一样的,这样就可以得出当M 为100时,已经得出有效解。

题目一:永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A 、B 两道工序加工。
设有两种规格的设备A1、A2能完成 A 工序;有三种规格的设备B1、B2、B3能完成 B 工序。
Ⅰ可在A 、B 的任何规格的设备上加工;Ⅱ 可在任意规格的A 设备上加工,但对B 工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工。
数据如表。
问:为使该厂获得最大利润,应如何制定产品加工方案?解:设设备A 1生产I 产品1x 件,产品II 生产2x 件,设备A 2生产产品I,3x 件,产品IIx 4件,产品IIIx 5件,设备B 1生产Ix 6件,IIx 7件,设备B 2生产Ix 8件,IIIx 9件,设备B 3生产Ix 10件。
由题意可得:Max Z=0.751x +1.152x +0.77533x +1.3611 x 4+1.9148 x 5-0.375 x 6-0.5 x7-0.447429x 8-1.230429 x 9-0.35 x 10ST.⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧957421086311098765432004000770001144000861000012976000105x x x x x x x x x x x x x x x x x x x x ==-+=---+≤≤+≤+≤++≤+经运算可得:**********************最优解如下*************************目标函数最优值为: 1146.41367867589变量最优解------- --------x1 1200x2 0x3 230x4 500x5 324x6 0x7 500x8 859x9 324x10 571约束松弛/剩余------- ---------1 02 23 04 05 36 07 08 0故设备A1生产I产品1200件,产品II生产零件;设备A2生产产品I,230件,产品II500件,产品III324件;设备B1生产I零件,II500件;设备B2生产I859件,III324件;设备B3生产I571件时,厂商可以获得最大利润1147元。

运筹学上机环节大纲更新2008-WINQSB版《运筹学》(上机)实验大纲一、制定本大纲的依据本大纲根据《运筹学》教学大纲对学生实验能力培养要求而制定。
二、对本门课程的实验具体要求三、本实验在《运筹学》课程教学中的地位与作用运筹学上机实验是验证、巩固和补充课堂讲授理论知识的必要环节,通过上机实验培养学生掌握使用成熟软件求解运筹学问题,特别是线性规划问题的技能。
四、学生应达到的实验能力与标准1.使用Excel求解线性规划问题,并能读懂结果分析报告2.使用QSB做线性规划问题,并能读懂结果分析报告五、讲授的基本理论和实验技术知识运筹学上机实验主要讲授常用运筹学求解软件的使用方法,能对实际问题能够建立模型并运用软件进行求解。
六、实验成绩的考核与评定方法根据学生的上机实验结果进行评定,给出成绩(占课程平时成绩的30%)。
实验一线型规划问题的Excel建模求解实验目的:掌握在Excel中建立线性规划模型和求解的方法实验内容:1.熟悉Excel求解线性规划的工具solver;2.利用Excel求解各种线性规划问题;实验步骤1. 熟悉Excel求解线性规划的工具solver案例1利用EXCEL求解线性规划123123123123min321; .431;,,0w x x xx x xs t x x xx x x第一步建模依次在相应的单元格内输入数据和公式,建模如图1图1线型规划的Excel模型第二步设置规划求解参数如图2,其中,"选项"中选取"假定非负"和"采用线性模型",其它采用默认选项,如图3图2 规划求解参数设置图3 选项设置第三步求解设置完毕后,单击图2中"求解"按钮,出现如图4规划求解结果对话框图4 规划求解结果对话框如图4所示,共提供3类报告,选择你想要的报告,单击确定按钮,完成运算,最后计算结果如图5图5 计算结果2.利用Excel求解各种线性规划问题;生产计划问题案例21:某工厂计划用现有的铜、铅两种资源生产A、B两种型号的电缆。

人力资源分配问题第一题(1)安排如下:x1=8,x2=0,x3=1,x4=1,x5=0,x6=4,x7=0,x8=6,x9=0x10=0,x11=0。
(2)总额为320,一共需安排20个班次;因为在13:00—14:00,14:00—15:00,16:00—17:00,分别存在2,9,5个工时的剩余,(例如11:00—12:00)安排了8个员工而在14:00-15:00剩余了九个所以可以安排一些临时工工作3个小时的班次,使得总成本更小。
(3)在18:00—19:00安排6个人工作4小时;在11:00—12:00安排8个人,13:00—14:00安排1个人,15:00—16:00安排1个人,17:00—18:00安排4个人工作3小时。
总成本最低为264元。
生产计划优化问题第二题产品1在A1生产数量为1200单位,在A2上生产数量为230单位,在B1上不生产,B2上生产数量为858单位,B3上生产数量为571单位;产品2在A1上不生产,在A2上生产数量为500单位,在B1上生产数量为500单位;产品3在A2上生产数量为324单位,在B2上生产数量为324单位。
最大利润为2293.29元。
第三题设Xi为产品i最佳生产量。
(1)最优生产方案唯一,为X1=1000、X2=1000、X3=1000、X4=1000、X5=1000、X6=55625、X7=1000. (2)如上图所示,产品5的单价价格为0-30时,现行生产方案保持最优。
(3)由于环织机工的影子价格为300,且剩余变量值为零,而其他几种资源的影子价格为0,剩余变量均大于0,所以应优先增加环织工时这种资源的限额,能增加3.33工时,单位费用应低于其影子价格300才是合算的。
(4)因为产品2对偶价格= -3.2<0 ,950>933.33,3.2*(1000-950)=160;所以当产品2的最低销量从1000减少到950时,总利润增加160元。

随着现代科学技术的飞速发展,运筹学作为一门应用广泛的交叉学科,已经渗透到了各个领域。
在大学期间,我有幸选修了运筹学这门课程,并通过上机实践深入学习了运筹学的基本原理和应用方法。
以下是我对运筹学上机实践的一些心得体会。
一、理论与实践相结合的重要性运筹学是一门理论与实践相结合的学科。
在课堂学习中,我们学习了线性规划、整数规划、网络流、决策分析等基本理论。
然而,这些理论知识的掌握仅仅停留在书本上,对于实际问题的解决能力还是有限的。
通过上机实践,我们可以将理论知识与实际问题相结合,提高解决实际问题的能力。
在上机实践中,我深刻体会到了理论与实践相结合的重要性。
首先,通过编程实现算法,可以让我们更加直观地理解算法的原理和步骤。
例如,在学习线性规划时,我们通过编写代码求解线性规划问题,可以清楚地看到目标函数、约束条件以及算法的迭代过程。
这种直观的理解有助于我们更好地掌握线性规划的基本原理。
其次,上机实践可以帮助我们检验和巩固课堂所学知识。
在编写代码的过程中,我们会遇到各种问题,如算法错误、数据异常等。
这些问题需要我们运用所学知识进行分析和解决。
通过不断尝试和修正,我们不仅能够巩固已学的知识,还能够提高自己的编程能力。
二、编程能力的提升运筹学上机实践对编程能力的要求较高。
在实践过程中,我逐渐认识到编程能力的重要性。
以下是我对编程能力提升的一些体会:1. 熟练掌握编程语言:在上机实践中,我们通常会使用一种或多种编程语言进行算法实现。
因此,熟练掌握编程语言是进行运筹学上机实践的基础。
我通过学习Python、MATLAB等编程语言,提高了自己的编程能力。
2. 熟悉算法实现:运筹学中的各种算法都有相应的编程实现方法。
在上机实践中,我们需要了解并掌握这些算法的实现方法。
例如,在求解线性规划问题时,我们需要了解单纯形法、内点法等算法的编程实现。
3. 优化代码结构:在编写代码时,我们需要注意代码的可读性、可维护性和可扩展性。
运筹学上机实验指导书重庆交通大学管理学院目录绪论运筹学上机实验软件简介第一章运筹学上机实验指导§1.1 中小型线性规划模型的计算机求解§1.2 大型线性规划模型的编程计算机求解§1.3线性规划的灵敏度分析§1.4运输问题数学模型的计算机求解§1.5目标规划数学模型的计算机求解§1.6整数规划数学模型的计算机求解§1.7 指派问题的计算机求解§1.8最短路问题的计算机求解§1.9最大流问题的计算机求解第二章LINGO软件基础及应用§2.1 原始集(primitive set)和派生集(derived set)与集的定义§2.2 LINGO中的函数与目标函数和约束条件的表示§2.3 LINGO中的数据§2.4 LINDO简介第三章运筹学上机实验及要求实验一.中小型线性规划模型的求解与Lingo软件的初步使用实验二.中小型运输问题数学模型的Lingo软件求解。
实验三.大型线性规划模型的编程求解。
实验四.运输问题数学模型的Lingo编程求解。
实验五.分支定界法上机实验实验六.整数规划、0-1规划和指派问题的计算机求解实验七:最短路问题的计算机求解实验八:最大流问题的计算机求解实验九:运筹学综合实验绪论运筹学是研究资源最优规划和使用的数量化的管理科学,它是广泛利用现有的科学技术和计算机技术,特别是应用数学方法和数学模型,研究和解决生产、经营和经济管理活动中的各种优化决策问题。
运筹学通常是从实际问题出发,根据决策问题的特征,建立适当的数学模型,研究和分析模型的性质和特点,设计解决模型的方法或算法来解决实际问题,是一门应用性很强的科学技术。
运筹学的思想、内容和研究方法广泛应用于工程管理、工商企业管理、物流和供应链管理、交通运输规划与管理等各行各业,也是现代管理科学和经济学等许多学科研究的重要基础。
实验一 使用LINGO 求解线性规划问题班级: 姓名: 学号: 评阅成绩: 已知如下线性规划模型:123max 303540z x x x =++1231231231233251823412229,,0x x x x x x x x x x x x ++≤⎧⎪++≤⎪⎨++≤⎪⎪≥⎩ 一、利用集的方法编写上述线性规划模型的LINGO 程序。
在LINGO 软件模型中编写本题的程序如下图1-1所示所示。
图1-1 LINGO 模型窗口截图点击LINGO 菜单下的Solve 选项,LINGO 软件求解所输入的模型,得到LINGO 运行状态窗口如图1-2所示图1-2 LINGO运行状态窗口截图运行结束后,关闭LINGO运行状态窗口,获得LINGO软件的结果报告窗口,如图1-3、1-4所示。
图1-3 LINGO结果报告窗口截图(一)图1-4 LINGO结果报告窗口截图(二)二、根据编写的程序,回答以下问题:1、哪些是原始集?答:var(j), const(i)是原始集2、哪个是派生集?该派生集是稠密集还是稀疏集?该派生集有多少个成员?答:A(i,j)是派生集,属于稠密集合,共有9个成员3、属性值“5”是属于成员(b1,x3)还是(b3,x1)的属性值?答:属于成员(b1,x3)的属性值三、根据程序的运行结果,回答以下问题:1、全局最优值是否已经找到?该值是多少?答:已经找到,最优值为1652、该模型求解一共迭代了多少次?答:共迭代了2次3、在求解结果的界面中,Variable、Value、Reduced Cost、Row、Slack or Surplus 和Dual Price分别表示什么?答:Variable表示运算时各定义变量的取值;Value表示给出最优解中各变量的值;Reduced Cost表示列出最优单纯形表中判别数所在行的变量的系数,表示当变量有微小变动时, 目标函数的变化率;Row表示行数;Slack or Surplus 表示给出松驰变量的值;Dual Price表示当对应约束有微小变动时, 目标函数的变化率。
运筹学上机材料2002年4月上机共8学时,4次,第次2学时运输问题:已知单位运价的产销平衡问题如下图:用Excel求解的思路是:设置初始工作表,正确表示各个量之间的关系,在规划求解参数中设置目标单元格及最小(大)值,并添加约束条件。
步骤如下:一、设置初始工作表。
1、在上图中区域B4:F7输入各项单位运价,区域B8:F8和区域G4:G7分别输入销量和产量。
2、按上图中第10行开始输入所示文字,其中区域B14:F17均输入初始值1(使用自动填充)。
3、在B18中输入公式=B8-SUM(B14:B17),然后自动填充到C18:F18中;在G14中输入公式=G4-SUM(B14:F14),然后自动填充到G15:G17中。
4、在B11中输入公式=SUMPRODUCT(B14:F17,B4:F7)二、求解。
1、打开“工具”菜单,选择“加载宏”选项,从“加载宏”对话框中选中“规划求解”后单击“确定”。
(注意:Office可能提示你要安装该选项)2、现在可以打开“工具”菜单,选择“规划求解”选项。
3、在中单击按钮,选择B11单元格。
然后选择“最小值”。
4、选择B14:F17作为可变单元格区域。
5、单击“添加”按钮,出现“添加约束”对话框。
6、首先添加变量非负约束:选择区域B14:F17,再选择“>=”,在第三个框中输入“0”,再单击“添加”。
如右图所示。
7、设置约束B18:F18=0,即销量无剩余。
再单击“添加”按钮。
8、设置约束G14:G17即产量无剩余。
最后单击“确定”按钮,回到“规划求解参数”对话框中,约束设置完成,如下左图所示。
9、单击“求解”按钮,即可得到结果如上右图所示。
上机练习:1、线性规划:运筹学书中P40页问题,并验证书上的结果。
2、运筹学书中P77页第29题。
3、运输问题运筹学书中P92页问题,其中M可取一个大数如1004、运筹学书中P100页第(3)小题。
上机考核内容:在2小时内完成1个线性规划问题和1个运输问题。
《实用运筹学》上机实验指导课程名称:运筹学/Operations Research实验总学时数:60学时一、实验教学目的和要求本实验与运筹学理论教学同步进行。
目的:充分发挥Excel软件这一先进的计算机工具的强大功能,改变传统的教学手段和教学方法,将软件的应用引入到课堂教学,理论与应用相结合。
丰富教学内容,提高学习兴趣。
要求:能用Excel软件中的规划求解功能求解运筹学中常见的数学模型。
二、实验项目名称和学时分配三、单项实验的内容和要求实验一线性规划(-)实验目的:安装Excel软件“规划求解”加载宏,用Excel软件求解线性规划问题。
(二)内容和要求:安装并启动软件,建立新问题,输入模型,求解模型,结果的简单分析。
(三)实例操作:求解习题1.1。
(1)建立电子表格模型:输入数据、给单元格命名、输入公式等;(2)使用Excel软件中的规划求解功能求解模型;(3)结果分析:如五种家具各生产多少?总利润是多少?哪些工序的时间有剩余,并对结果提出你的看法;(4)在Excel或Word文档中写实验报告,包括线性规划模型、电子表格模型和结果分析等。
案例1 生产计划优化研究某柴油机厂年度产品生产计划的优化研究。
某柴油机厂是我国生产中小功率柴油机的重点骨干企业之一。
主要产品有2105柴油机、x2105柴油机、x4105柴油机、x4110柴油机、x6105柴油机、x6110柴油机,产品市场占有率大,覆盖面广。
柴油机生产过程主要分成三大类:热处理、机加工、总装。
与产品生产有关的主要因素有单位产品的产值、生产能力、原材料供应量与生产需求情况等。
每种产品的单位产值如错误!未找到引用源。
所示。
表 C-1 各种产品的单位产值为简化问题,根据一定时期的产量与所需工时,测算了每件产品所需的热处理、机加工、总装工时,如表 C-2所示。
表 C-2 单位产品所需工时同时,全厂所能提供的总工时如表 C-3所示。
表 C-3 各工序所能提供的总工时产品原材料主要是生铁、焦碳、废钢、钢材四大类资源。
运筹学上机攻略
一、规划求解的预备知识
1、打开Excel软件的工具→→加载宏→→规划求解(选定),单击确定;加载
宏成功后,关闭再重新打开excel。
注明:这个宏是office自带的,一般情况下不启用的哦,所以要加载。
2、如果上述方法,不能成功加载成功,请到网上下载规划求解宏solver.xla。
二、规划求解的操作步骤
1、首先将已经建立好的书面数学模型,按照Excel的输入规定,将逻辑公式输
入到打开的工作薄文件的一个电子表格中;
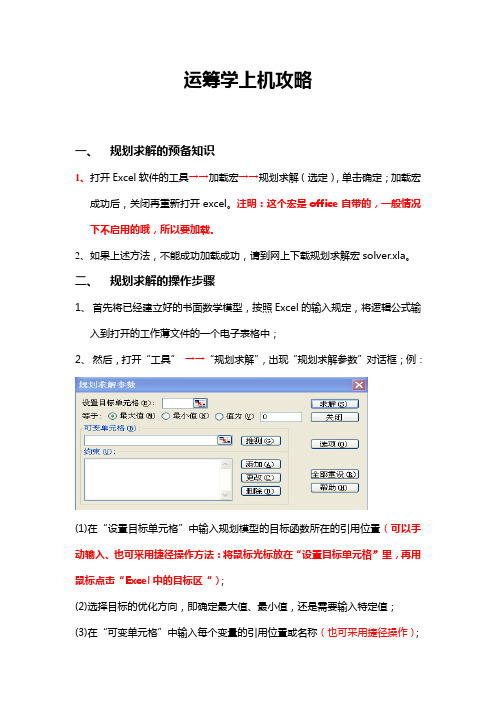
2、然后,打开“工具”→→“规划求解”,出现“规划求解参数”对话框;例:
(1)在“设置目标单元格”中输入规划模型的目标函数所在的引用位置(可以手动输入、也可采用捷径操作方法:将鼠标光标放在“设置目标单元格”里,再用鼠标点击“Excel中的目标区“);
(2)选择目标的优化方向,即确定最大值、最小值,还是需要输入特定值;
(3)在“可变单元格”中输入每个变量的引用位置或名称(也可采用捷径操作);
(4)鼠标点击“添加”、修改或删除,打开下一级对话框,开始对规划模型的约束对话,并在输入完毕后还回“规划求解参数”主对话框。
例:
(注意:单元格引用位置也可以采用捷径操作)、约束值手动输入。
(5)鼠标点击“选项”,打开下一级对话框,开始规划模型的选项对话,并在输入完毕后还回“规划求解参数”主对话框。
3、以上工作完毕后,点击“求解”。
三、例子
变量:甲的产量X1,乙的产量X2
目标函数:maxZ(X1,X2)=4X1+5X2
约束条件:X1+X2≤45
2X1+X2≤80
X1+3X2≤90
X1,X2≥0
第一步:在EXCEl中,输入逻辑公式,如下图:
第二步:打开“工具”→→“规划求解”,按步骤2的1-4步操作,出现下图:
【引用位置($C$6、$C$9、$C$10)等,可以手动输入、也可采用捷径操作方法:将鼠标光标放在“设置目标单元格”里,再用鼠标点击“Excel中的目标区“)】
第三步:求解结果:
Microsoft Excel 11.0 运算结果报告
工作表 [Book1]Sheet1
报告的建立: 2011-9-16 17:29:14
目标单元格 (最大值)
单元
格
名字初值终值
$C$6 目标函数0 202.5
可变单元格
单元
格
名字初值终值
$C$9 决策变量X1 0 22.5
$C$10 决策变量X2 0 22.5
约束
单元
格
名字单元格值公式状态型数值
$C$12 约束A 45 $C$12<=45 到达限制
值
$C$13 约束B 67.5 $C$13<=80 未到限制
值
12.5
$C$14 约束C 90 $C$14<=90 到达限制
值
$C$15 甲产量22.5 $C$15>=0 未到限制
值
22.5
$C$16 乙产量22.5 $C$16>=0 未到限制
值
22.5。