4,《结构力学》三铰拱

下面我们研究拱截面的受力情况。
QM
R
N
e
拱截面一般承受三种内力：M、Q、N。 若用合力 R 代替截面所有内力，则其偏心距为e = M/N，显
然我们可以求出各个截面的合力大小、方向和作用点。
P1 P2
作用线
G
F
rD
D
k2
C
k1
A
RA
RA
P1
D 大小和方向 o 23
P2
RB
P3
P3
（1）确定各截面合力的
q=2kN .m
P=8kN
例 1、三铰拱及其所受荷载如
y
34
5
图所示拱的轴线为抛物线方程
2 1
2
y2
0
6 7 8
f=4m
y
4f l2
xl x
计算反力并绘
x
制内力图。
A
7.5kN
x2=3m 6m
VA 11kN
B
3m
H 7.5kN （1）计算支座反力
6m
VB 9kN
VA
VA
2
698 12
3
例3、设三铰拱上承受填土荷载，填土表面为一水平面，试求拱的合理轴线，设
填土的容重为，拱所受的分布荷载为 q qC y。
[解]由拱截面弯矩计算式 M M Hy 在本例的座标系中可表达为：
M M H y M H f y 0
M y f
H
因事先 M 得不到，故改用q(x)和y(x)表示：
§5-3 拱的合理轴线 在固定荷载作用下，使拱处于无弯矩状态的轴线称为合理 轴线。由上述可知，按照压力曲线设计的拱轴线就是合理轴线。 从结构优化设计观点出发，寻找合理轴线即拱结构的优化选型。

如下所示结构在竖向 荷载作用下，水平反力 等于零，因此它不是拱 结构，而是曲梁结构。
下面所示结构在竖向荷 载作用下，会产生水平反 力，因此它是拱结构。
FP FP
曲梁
三铰拱
二、 拱的类型
三铰拱
两铰拱
无铰拱
超静定拱
拉杆拱 静定拱
三、 拱的各部分名称 拱顶
C
拱轴线 拱高 f
B
拱趾 A
起拱线
跨度 l
f l
f
B
A
0 FYB
FYB
FPi ai
L
xk
L1 L
FP2 k C
L2
FP3
取左半跨为隔离体：
FP1
M
C
0
A
0 FYA L1 FP1 L1 a1 FP 2 L1 a2 M C FH f f
B
反力计算公式：
F F 0 YA YA 0 FYB FYB 0 MC H A H B H f
P P P1 P2
P
P
P1
P2
结点单元
杆件单元
杆件体系 单元
1 静定结构受力分析的方法 二、平衡方程的数目 单元平衡方程的数目=单元的自由度数，不一定等 于单元上未知力的数目。
P P1
P2
P
P1
P2
结点单元
杆件体系 单元
1 静定结构受力分析的方法 三、计算的简化与截取单元的次序 计算简化的原则：避免解联立方程，尽量使一个方程中只
FP2 FP1 D
E
C
FP3 FP1 FP2 F B
FRA
A
o
FRA
FRB
FP3

拱架搭设
根据设计要求，选用合适的材料搭设拱架；
施工流程与工艺要求
02
01
03
拱体安装
按照从两端向跨中的顺序，对称安装拱体构件；
拱顶合拢
在拱顶设置临时支撑，确保拱体稳定；
施工监测
对施工过程进行实时监测，确保施工安全和质量。
施工流程与工艺要求
工艺要求 拱架搭设应符合设计要求，确保稳定性和承载力；
拱体安装应保证构件对接准确，避免出现错位和扭曲；
施工流程与工艺要求
01
临时支撑设置应合理，确保拱体 在合拢过程中保持稳定；
02
施工监测应实时进行，及时发现 和解决施工中的问题。
安装方法与注意事项
安装方法 采用分段吊装法，将拱体分成若干段，分别吊装到位；
对接安装时，应保证对接位置准确，避免出现错位和扭曲；
安装方法与注意事项
• 合拢时，应设置临时支撑，确保拱体稳定。
结构力学5三铰拱课件
目
CONTENCT
录
• 三铰拱概述 • 三铰拱的力学分析 • 三铰拱的设计与计算 • 三铰拱的施工与安装 • 三铰拱的维护与加固
01
三铰拱概述
定义与特点
定义
三铰拱是一种静定结构，由两个 固定端和三个铰链支承构成。
特点
拱顶在竖向荷载作用下主要承受 压力，并通过铰链传递水平推力 ，保持拱的平衡。
保持三铰拱的清洁，避免 积尘、腐蚀等影响其使用 寿命的因素。
紧固与润滑
对三铰拱的连接部位进行 紧固，对活动部位进行润 滑，确保其正常运转。
常见问题与处理方法
1 2
结构损伤
如发现三铰拱出现裂纹、变形等损伤，应立即采 取措施进行修复或更换。
连接松动

第二节 竖向荷载作用下三铰拱的受力分析
当两支座在同一水平线上时，称为等高拱或平拱，否 则称为斜拱。分析竖向荷载作用下三铰拱的内力和反 力时，与同跨度、同荷载的简支梁相对比，以便于计 算和对比分析拱的受力性质。
FP1
C FP2
f
A
B
l
FP1
FP2
1 竖向荷载作用下拱反力计算 mB 0
y
A FAx
第一节 三铰拱的组成和类型
2. 三铰拱的构成
矢高：起拱线至拱顶的 竖直距离。
拱趾
拱顶
矢高f 起拱线
跨度L
拱轴 拱趾
第一节 三铰拱的组成和类型
2. 三铰拱的构成
带拉杆的拱：在 屋架中，为消除 水平推力对墙或 柱的影响，在两 支座间增加一拉 杆，由拉杆来承 担水平推力，桥 梁中应用也非常 广泛。
第一节 三铰拱的组成和类型
yk
A
B
k
C
Fy' 0
F0 Ay
F0 Sk
F0 Ay
P1
F0 By
FS k FAy cosk P1 cosk FH sin k
M 0 F0 x Px a
k
Ay k
1k
1
FA0y P1 cosk
FS
0 k
c os k
FH
FH sin k
sin k
FN k
Fx' 0
FAy sink P1 sink FH cosk
在工程实践中，由于载荷的多样性，不可能有真正的无弯矩 拱，但是可以想象，接近合理拱轴的设计，应当是可行的方 案。赵州桥是我国隋代工匠李春建造的一个著名的范例。
第一节 三铰拱的组成和类型
1、工程上使用的拱结构实例

4 4 yk 2 4(16 4) 3m 求MK 16 MK 0 MK 12.5 4 10 3 20kN.m(下拉)
求MJ
yJ 3m
M
J
0
M J 7.5 4 10 3 30 30 0
3. 求FQ、FN的计算公式
拱轴任意截面D切线与水平线夹角为φ。 相应代梁中， F 设为正方向。
FP1=15kN K FHA A yk 4m
l/2
C f=4m
MC 0
FVA
4m
l l FVA FHA f FP1 0 2 4 0 MC 1 l l FHA ( FVA FP1 ) () f 2 4 f
0 上式中，M C 为代梁C截面弯矩。
M FHB () f
0 ND右 QD右 sin D H cosD 12 0.555 10.5 0.832 15.4kN
重复上述步骤，可求出各等分截面的内力，作出内力图。
三、三较拱的合理轴线
在给定荷载作用下，三铰拱任一截面弯 矩为零的轴线就线为合理拱轴。 三铰拱任一截面弯矩为 M M FH y
超静定拱
拉杆拱 静定拱
拱顶
C
拱轴线 拱高 f
B
拱趾
A
起拱线 跨度 l
f l
f
高跨比
l 通常 f l 在1-1/10之间变化，f 的值对内力有 很大影响。
工程实例
拱桥 （无铰拱）
超静定拱
世界上最古老的铸铁拱桥（英国科尔布鲁克代尔桥)
万县长江大桥：世界上跨度最大的混凝土拱桥
二、三铰拱的计算
A 12.5kN K左 Fº ＝12.5kN QK左 A 12.5kN

10.5 12 12
sinϕ D = −0.555 cosϕ D = 0.832
A
3m
0 M = M D − Hy D = 12 × 3 − 10.5 × 3 = 4.5kN ⋅ m 0 QD左 = QD左 cos ϕ D − H sin ϕ D = (− 2 )× 0.832 − 10.5 × (− 0.555) = 4.16kN 0 N D左 = −QD左 sin ϕ D − H cos ϕ D = −(− 2 )× (− 0.555) − 10.5 × 0.832 = −9.85kN 0 QD右 = QD右 cos ϕ D − H sin ϕ D = (− 12 )× 0.832 − 10.5 × (− 0.555) = －4.16kN
在竖向荷载作用下，三铰拱 平拱 的支座反力有如下特点： 平拱)的支座反力有如下特点 在竖向荷载作用下，三铰拱(平拱 的支座反力有如下特点： 1）支座反力与拱轴线形状无关，只与荷载及三个铰的位置有关。 ）支座反力与拱轴线形状无关，只与荷载及三个铰的位置有关。 2）竖向支座反力与拱高无关，水平推力与拱高有关。 ）竖向支座反力与拱高无关，水平推力与拱高有关。 3）当荷载和跨度一定时，拱的水平推力H与拱高 f 成反比，即拱高 ）当荷载和跨度一定时，拱的水平推力 与拱高 成反比， f 越大，水平推力 H 越小，反之，拱高 f 越小，水平推力 越大。 越大， 越小，反之， 越小，水平推力H越大 越大。 趋近于零时， 推力） 当拱高 f 趋近于零时，水平反力 H（水平推力）趋近于无穷大，此 （水平推力 趋近于无穷大， 三铰在一条直线上， 时A、B、C三铰在一条直线上，构成瞬变体系，不能作为结构 、 、 三铰在一条直线上 构成瞬变体系，不能作为结构.
三、内力图 （1）画三铰拱内力图的方法：水平基线描点法。 画三铰拱内力图的方法：水平基线描点法。 （2）画三铰拱内力图的步骤 1）计算支座反力 ） 2）计算拱截面的内力（可以每隔一定水平距离取一截面， ）计算拱截面的内力（可以每隔一定水平距离取一截面， 也可以沿拱轴每隔一定长度取一截面）。 也可以沿拱轴每隔一定长度取一截面）。 3）按各截面内力的大小和正负绘制内力图。 ）按各截面内力的大小和正负绘制内力图。 注意： 注意： 1）仍有 Q=dM/dx 即剪力为零处弯矩为极值； 即剪力为零处弯矩为极值； ） 2） M、Q、N图均不再为直线（参见书本 60 图4-6）； 图均不再为直线（ ） 图均不再为直线 参见书本P ）； 3）集中力作用处 图将发生突变； 图将发生突变； ）集中力作用处Q图将发生突变 4）集中力偶作用处 图将发生突变。 图将发生突变。 ）集中力偶作用处M图将发生突变

B
②剪力、轴力计算公式
FQFQ 0co-sFHsin
F0yA φ FP1
M0
F0yB
FNFQ 0sin-FHcos
KM
FN
F
0 Q
—相应简支梁对应截面上的剪力
φ φ—截面处拱轴切线倾角，在左半拱
FH A
y φ FQ
为正(右半拱为负)
φ
x
FVA φ
◆ 拱截面轴力较大，且一般为压力
例3-5 作图示三铰拱的内力图，拱轴为抛物线，其方程为
1kN/m C
f=4m x
FQ0L 1kN
FV A l1=8m
4m
l=16m
4kN
D
B FH B
4m
FV B
FQ0R 5kN
1kN/m
A
C
4kN B
F0yA
F0yB
F QLF Q 0L co-sFHsin 1 0 .89 6 ( 4 0 .44 ) 4 1 .7 7k 8 2 N
F Q RF Q 0c R o -sF Hsin 5 0 .8 9 6 ( 0 4 .44 ) 4 1 7 .7k 2 8N 9
四 三铰拱的合理拱轴线（reasonable axis of arch） 1 合理拱轴线的概念 在给定荷载作用下，使拱处于无弯矩状态的拱轴线，称 为拱的合理拱轴线
2 合理拱轴线的确定 根据荷载作用下，任一截面弯矩为零条件确定。如竖向 荷载作用下的三铰拱：
MM0FHy0 y M0
FH
通过由调此整可拱见的，轴当线拱，上使荷拱载在为确已定知荷时载，作只用要下求各出截相面应上简的支弯梁 矩值的为弯零矩，方这程时，拱除截以面支上座只水有平通推过力截FH面，形即心可的求轴得向合压理力拱作轴 用，的其轴压线应方力程沿截面均匀分布，此时的材料使用最为经济

9 / 13
À
第四章 静定拱
试求图示对称三铰拱在均布荷载作用下的合理拱轴线
q y A x q f C B
FH=ql2/8f M0=qlx/2-qx2 /2 =qx(l-x)/2 y=M0/FH=4fx(l-x)/l2
l
x
抛物线À
10 / 13
第四章 静定拱
荷载布置改变，合理拱轴亦 改变 荷载确定、拱脚位置确定， 则顶铰位置决定水平反力， 因此，有无限多个相似图形 可作合理拱轴 三铰位置确定，合理拱轴唯 一确定 设计时只能根据主要荷载选 择近似合理拱轴
第四章 静定拱 §4-1 概述
三铰拱(three-hinges arch)的构成
拱顶 拱轴线 拱高 拱址 起拱线 拱跨 拱址
1 / 13
ÀБайду номын сангаас
第四章 静定拱
1)拱的分类
三铰拱 拉杆拱1
两铰拱
无铰拱
拉杆拱2
斜拱
2 / 13
À
第四章 静定拱
2)拱的受力特点
FP
曲梁
FP • 在竖向荷载作用下 会产生水平推力。
6 / 13
À
第四章 静定拱
拱的内力图
− y ⎤⎧M ⎫ ⎧M ⎫ ⎡1 0 ⎪ 0⎪ ⎪ ⎪ ⎢ ⎥ ⎨FS ⎬ = ⎢0 cosϕ − sinϕ⎥⎨ FS ⎬ ⎪F ⎪ ⎢0 sinϕ cosϕ ⎥⎪ F ⎪ ⎦⎩ H ⎭ ⎩ N⎭ ⎣
0
由于拱轴线是弯曲的，所以内力图都是曲线形 的，内力图要通过逐点描图的方法绘制。
拱
• 由于水平推力的存 在，使得拱内弯矩大 大减小。
3 / 13
À
第四章 静定拱 §4-2 三铰拱的计算

例题4－1 求图4－5a所示圆弧形曲杆任意截面的内力M、V、N。 解:以极坐标φ表示B截面的位置，取图4－5c所示BC部分隔离体，
设B截面的内力分别为Mφ、Vφ、Nφ, 参照图4－5b并考虑到ds=Rdα, 由平衡条件得 ∑MB=0 Mφ=∫S qdsRsin（φ－α） =qR2∫0φsin(φ-α）dα=qR2（1－cosφ) 式 (4-1)
ND VD0sinφD Hcos φD （4-19）
五. 斜拱的支座反力和内力计算
连接A、B，先将A和B处的支座
反力分别沿竖向和起拱线方向分解
为两个相互斜交的分力V ’A和 H’A和 V ’B 和H ’B 。 根据上述平衡条件可得：
V
’A＝V
0A，
V
’B
＝V
0 B
H’A＝H ’B＝H’＝M 0C/ f ’
)
HB
VA VA0
VB
VB0
X 0: HA HB H
MC VAl1 P1(l1 a1) Hf 0
H
1 f
[VAl1
P1
(l 1
a 1 )]

M
0 C
VAl1
P1 (l1
a1)
H
M
0 C
f
（4-16）
a1
b1
a2
y
P1 D
φD
HA A
yD f
x xD
VA
P1
MD
D
ND
VD
HA A
产生水平支座反力（推力）HA、HB。水平支座反力对拱截面 产生负弯矩（上侧受拉），从而使得三铰拱截面上的内力弯矩 小于荷载和跨度相同的相应简支梁上各对应截面上的弯矩值， 省材料，空间跨度大，但比梁需要更为坚固的基础或支承结构。

三铰拱
一、概述
（一）工程应用
赵州桥
永定河七号铁路桥（150m）
BEH办公大楼（78m）
菜园坝长江大桥建设方案
（二）拱结构类型
（三）拱的构造
高跨比（矢跨比）： 拱高与跨度之比，即 f l 。 高跨比一般为1～1/10，常用1/4 ～1/6。 拱轴线的形状可以为抛物线、 圆弧曲线等。
（四）拱的特点（拱的共性，并非三铰拱特有）
1.提出公式的目的 （1）求三铰拱内力的方法：截 取 力 平 （2）遇到类似情况，可以直接用公式计算。 2.公式的说明 （1）适用范围：对称三铰拱，任意竖向荷载。 （2）公式中各参数的含义 （3）分析拱的内力特点
M K = M K − HyK
QK = QK cos ϕ K − H sin ϕ K
N K = QK sin ϕ K + H cos Βιβλιοθήκη K例三、合理拱轴线
（一）定义
合理拱轴线：在给定荷载作用下拱所有截面上只承受轴力，弯矩为零时的拱轴线。
（二）合理拱轴线的形状
MK = M − HyK = 0
0 K
M(x) = M0 (x) − Hy(x) = 0 ⇒ y(x) = M (x) / H
0
⇒ yK = M / H
0 K
0 H = MC f
1.曲杆
2.竖向荷载作用下有水平推力 在竖向荷载作用下产生水平推力的曲杆结构称为拱。 3.由于水平推力的存在，使M<M0（可以小到100%）。 4.内力一般有M、Q、N，许多情况下N是主要内力。
（五）拱的性能
1.拱比梁更能发挥材料的作用，适用于较大的跨度和荷载。 2.拱主要受压，便于利用抗压性能好而抗拉性能差的材料。 3.三铰拱给基础施加向外的推力，所以基础比梁的基础要大。

（A,B,C三铰在一直线上，成为几何瞬变体。）
.
②拱内力计算：
QM
P1
N
D
HA
VA
弯矩：受拉侧做弯矩图； 剪力：垂直于拱轴线的切线（顺时针为正)； 轴力：平行于拱轴线的切线(拉为正)。
.
a1
M
P1 D
y HA x
VA
•弯矩：
由 MD0
M V A x P 1 ( x a 1 ) H y 0 M M oH y
C
Mc0q2l /8
l
Mc0 / 6
Mc0 / 6
B
A
C
B
Mc0 / 6
0.207 l 0.586 l 0.207 l
优点：方便，简单； 缺点：截面仍有弯矩。
.
②三铰曲拱：
f MM0Hy (HM c0/ f)
优点：截面弯矩很小或无弯矩； 缺点：曲线杆件施工复杂。
.
③桁架： 上弦、下弦承受弯矩；腹杆承受剪力。
其中：M o V A x P 1 (x a 1 )— 对应点的简支梁弯矩
.
Qo
Q
M
P1
φ
DH
HA
VA
•剪力：
其中：
QQ oco sH sin
Q VAP 1–– 对应点的简支梁剪力
— 切线与水平线所成锐角
（由水平向逆时针为正）
+φ -φ
左右
.
Qo M N
P1
φ
DH
y
HA x
•轴力：
VA
N Q s i n H c os
q M
qr
C
d θ
A
r
任意截面内力：
M q2r(1co )so qrdrsin () q2r(1co )sq2r(1co )s0

0 Q
FS
I l/2
FVB
【例2】求图示三铰拱式屋架在竖向荷载作用下的支反力和内力。 解： (1) 计算支座反力
q
0 VB
FH 0, FV A F , F V B F
0 VA
y FH FVA

A
C
x
f
B FVB
0 MC (2)计算拉杆内力： S F f
(3)计算拱身内力
钢拉杆（拉力FS） l/2 l/2 l
(2) 由于推力的存在（前两式右边第二项），拱与相应简 支梁相比：其截面上的弯矩和剪力将减小。弯矩的降低， 使拱能更充分地发挥材料的作用。
(3) 在竖向荷载作用下，梁的截面内没有轴力，而拱的截
面内轴力较大，且一般为压力（拱轴力仍以拉力为正、压 力为负）
三铰拱的内力图
1.画三铰拱内力图的方法 描点法。 2.画三铰拱内力图的步骤 1）计算支座反力 2）计算拱圈截面的内力（可以每隔一定水平距离取 一截面，也可以沿拱轴每隔一定长度取一截面）。 3）按各截面内力的大小和正负绘制内力图。 注： 1）仍有Q=dM/ds 即剪力等零处弯矩达极值； 2）M、Q、N图均不再为直线； 3）集中力作用处Q 图将发生突变； 4）集中力偶作用处M 图将发生突变。
0 FVA
l/2
FCx
I
FCy
C
FP3
F B I
FS
0 MC
FS
l/2
f
FVB
(3)计算拱身内力
在无拉杆三铰拱的内力计算式中，只须用FS去取代FH， 即可得出有水平拉杆拱身内力计算式为
M M FS y
0
I
FCy
C
FCx
FP3
F B

稳定性分析对于结构的整体稳定性和安全性具有 重要意义。
03
三铰拱的设计与优化
设计原则与步骤
确定设计要求
明确三铰拱的设计目标，如承载能力、稳定性、 经济性等。
截面设计
根据计算出的内力和弯矩，设计三铰拱的截面尺 寸和形状。
结构分析
对三铰拱进行受力分析，计算出各截面的内力和 弯矩。
稳定性分析
对三铰拱进行稳定性分析，确保其在承载过程中 不会发生失稳。
3D打印技术
3D打印技术能够实现复杂结构的快速 、精确制造，为三铰拱的原型制作和 试验提供便利。
未来发展方向与趋势
跨学科融合
结构力学与材料科学、计算机科 学、人工智能等学科的交叉融合，
将推动三铰拱在理论和实践上的 创新。
绿色与可持续发展
在未来的发展中，三铰拱的设计和 建造将更加注重环保和可持续发展， 如采用可再生材料和节能技术。
智能化与自动化
随着智能化和自动化技术的发展， 三铰拱的设计、建造和监测将趋向 于智能化和自动化，提高效率和安 全性。
THANK YOU
感谢聆听
案例分析与实践
案例一
某桥梁的三铰拱设计，通过优 化设计，提高了桥梁的承载能 力和稳定性。
案例二
某工业厂房的三铰拱设计，采 用轻量化设计，降低了结构的 自重。
案例三
某大型场馆的三铰拱设计，通 过参数优化，实现了结构的优 化和美观。
04
三铰拱的施工与维护
施工工艺与要点
01
02
03
04
施工准备
确保施工场地安全，检查施工 材料质量，制定施工计划和安
100%
建筑工程
在建筑工程中，三铰拱可用于大 型工业厂房、仓库、展览馆等建 筑的屋盖结构。

q( x) p( x) ds dx
dx p(x) ds x
y
中南大学
退出
返回
18:50
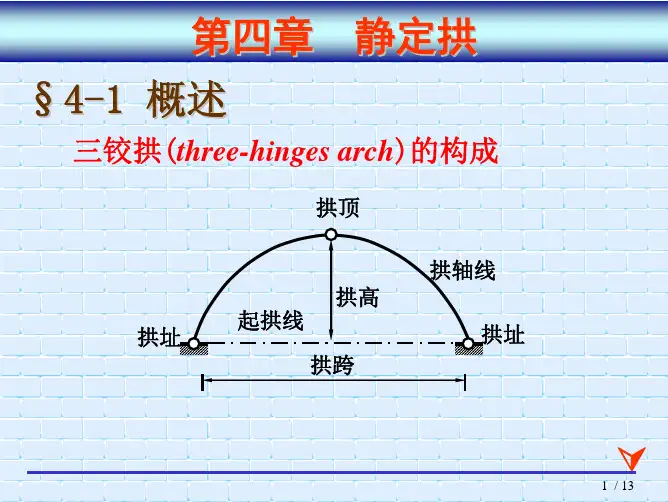
§4-3 三铰拱的合理拱轴线
将 q( x) p( x)
2
结构力学
ds dx
代入方程（4-5），得
2
d y q( x) p( x) ds p( x) dy 1 2 dx FH FH dx FH dx
由于规定y 向上为正, x 向右为正，q 向下为 正，故上式右边为正号。
中南大学
退出
返回
18:50
§4-3 三铰拱的合理拱轴线
或
结构力学
d dy dx dx dy 1 dx
1
2

p( x) FH
p ( x) dy sh dx. FH dx 如p(x)=常数=p ，则
中南大学
退出
返回
18:50
§4-2 三铰拱的数值解
(3) 求内力 由水平推力 FH 82.5 kN 得 0
结构力学
(2) 求支座反力,结果为： FVA 105 kN , FVB 115 kN
FSD 105 kN 100 kN 5 kN
FSD FS0D cos D FH sin D
返回
中南大学
退出
18:50
§4-2 三铰拱的数值解
与代梁相比较有：
0 FVA FV A 0 FVB FVB 0 MC FH f
结构力学
F F K A x x l/ 2 FVA f B l/ 2 FVB FHB C F
y
F HA
F1 A

桥梁工程
三铰拱广泛应用于桥梁工程中， 如公路桥、铁路桥和立交桥等。
100%
工业建筑
三铰拱适用于工业建筑中的大型 厂房、仓库等结构，能够承受较 大的竖向荷载和水平荷载。
80%
公共建筑
三铰拱也适用于公共建筑中，如 体育馆、会展中心等大型建筑， 能够提供大跨度和高承载能力的 结构体系。
02
三铰拱的力学分析
定位与调整
在吊装完成后，对三铰拱的位 置和角度进行调整，确保其符 合设计要求三铰拱的各个部件连接牢 固、可靠。
防腐与涂装
在施工完成后，对三铰拱进行 防锈蚀处理和涂装，提高其耐 久性和美观度。
施工安全
安全措施
在施工过程中，采取一系列安全措施，如设置安全警示标志、配 备安全带和安全帽等，确保施工人员的安全。
在基础上按照设计要求拼装三铰拱的各个部件，确保 拱体的几何尺寸和位置准确。
04
固定与调整
通过焊接或螺栓连接等方式将拱体固定在基础上，并 进行必要的调整，确保拱体的稳定性和承载能力。
05
施工监测
在施工过程中，对三铰拱的各项参数进行监测，确保 施工质量和安全。
安装技术
01
02
03
04
吊装方法
根据三铰拱的重量和尺寸，选 择合适的吊装机械和吊装方法 ，确保吊装过程中的安全和质 量。
三铰拱的特点
稳定性好
由于三铰拱具有静定结构的特点，因此其稳定性较 好，不易发生侧向失稳或扭转失稳。
承载能力强
三铰拱的承载能力较强，能够承受较大的竖向荷载 和水平荷载。
适用范围广
三铰拱适用于各种类型的建筑结构，如桥梁、厂房 、仓库等，尤其适用于需要承受较大荷载和跨度的 结构。
三铰拱的应用场景

q
FH A FVA
C f
l /2
l /2
B FH FVB
5.3三铰拱的合理轴线
三铰拱的合理拱轴计算应用
q A
x
代梁
合理拱轴为抛物线， 因此，房屋建筑中拱 的轴线通常用抛物线
y M0 FH
M 0 1 qx(l x) 2
FH

M
0 C
f

1 f
1 ql2 8

ql 2 8f
8f 1
4f
y
FHA A
P1=15kN
P2=5kN
C
K
J
yk f=4m yJ
B FHB x
FVA
4m
4m
l/2
4m
4m FVB
l/2
拱轴方程为
y=
4f l2
x(l x)
5.2三铰拱的内力分析
内力分析应用——求支座反力
P1=15kN
A K
4m 4m
C 4m
P2=5kN
B J
4m
代梁
l/2
l/2
FV0A FVA
5.3三铰拱的合理轴线
竖向荷载作用下三铰拱的合理拱轴
M M 0 FH y
M 0
y M0 FH
FH

M
0 C
f
对于不同的荷载，其合理轴线 不同。
在荷载、跨度给定时，合理拱
轴线 随 f பைடு நூலகம்不同而有多
条,不是唯一的。
5.3三铰拱的合理轴线
三铰拱的合理拱轴计算应用
求三铰拱在均布荷载作用下的合理拱轴。
d1 P1 MD ND
D xD yD QD