《微波技术》习题解(一、传输线理论)

max
I
max
m in
m in
m in
所以
P(z)
1
V
2 max
•
1
1
I
2
• Z0
2 Z0 2 max
根据这个表达式：
P(z)
ห้องสมุดไป่ตู้
1
V
2 max
•
1
1
I
2
• Z0
2 Z0 2 max
我们可以分析，当传输线的耐压一定或者能载的
电流一定的时候，驻波比越小，所能传输的功率 就越大，因此我们的滤波器在考虑功率因素的时 候，在我们的谐振杆和盖板距离一定，即它们之 间的耐压一定的情况下，驻波比越小的滤波器能 承受的功率就越大。
c. 输入阻抗分布特点： 前面分析过，终端短路传输线上的输入阻抗为：
Zin jZ 0 tan l
可见，终端短路线的输入阻抗为纯电抗，并随距离 z而交替表现为感抗或容抗，每隔1/4波长，阻抗 的性质改变一次，每隔1/2波长，阻抗就重复一 次，由前面的波形图可以清楚的理解。利用短路 线的这种特性，可以做成微波纯电抗元件或者谐 振回路。同轴滤波器的单腔谐振的原理就是从这 里分析得来的。
V (z) V0 (e jz e jz ) V0 (e jz e jz ) 2 jV0 sin z
I (z) V0 (e jz e jz ) V0 (e jz e jz ) 2 V0 cosz
Z0
Z0
Z0
可见，负载上电压为0，电流最大，这与普遍
规律正好吻合。
此时传输线上距离负载l处的输 入阻抗为
Zin
V (l) I (l)
2V0 c 2 jV0
o（s l） sin（ l）

Dz传输线上的等效电路
§1.1 传输线方程
应用基尔霍夫定律：
v( z, t ) Dz z i( z, t ) i( z Dz, t ) i( z, t ) Dz z v( z Dz, t ) v( z, t )
上式两端除以Dz，并令Dz→0，可得一般传输线方程 （电报方程）：
如传输线上无损耗，则为无耗传输线。即R=0, G=0。
有耗线
无耗线
§1.1 传输线方程
对于铜材料的同轴线（0.8cm—2cm），其所填充介质为
r 2.5,
则其各分布参数为：
108 S / m
当f =2GHz时
可忽略R和G的影响。——低耗线
§1.1 传输线方程
P17表2.1-1给出了双导线、同轴线和平行板传输线的 分布参数与材料及尺寸的关系。
l
而传输线的长度一般都在几米甚至是几十米之长。 因此在传输线上的等效电压和等效电流是沿线变化的。
——→与低频状态完全不同。
§1.1 传输线方程
传输线理论 长线理论
传输线是以TEM导模方式传 输电磁波能量。 其截面尺寸远小于线的长度， 而其轴向尺寸远比工作波长大 时，此时线上电压只沿传输线 方向变化。
§1.1 传输线方程
均匀传输线
沿线的分布参数 Rl， Gl ， Ll ， Cl与距 离无关的传输线
不均匀传输线
沿线的分布参数 Rl， Gl ， Ll ， Cl与距 离有关的传输线
§1.1 传输线方程
3) 均匀传输线的电路模型
均匀传输线
单位长度上的分布电阻为Rl、分布电导为Gl、分布电容 为Cl、分布电感为Ll, 其值与传输线的形状、尺寸、导 线的材料、及所填充的介质的参数有关。

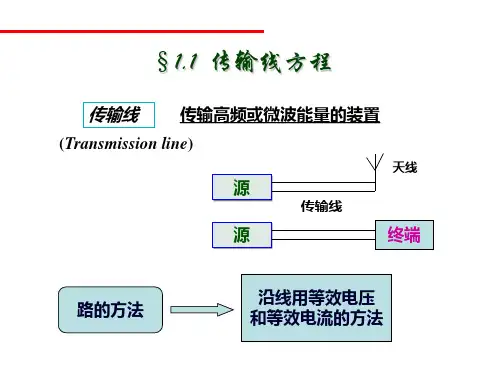
1-1什么是行波，它的特点是什么，在什么情况下会得到行波；什么是纯驻波，它有什么特点，在什么情况下会产生纯驻波？解：当传输线是无限长，或其终端接有等于线的特性阻抗的负载时，信号源传向负载的能量将被负载完全吸收，而无反射，此时称传输线工作于行波状态，或者说，传输线与负载处于匹配状态。

在行波状态下，均匀无耗线上各点电压复振幅的值是相同的，各点电流复振幅的值也是相同的，即它们都不随距离z 而变化；而且，电压和电流的瞬时值是相同的。

当负载l c Z Z =时，反射波为零，由此得到行波。

从信号传向负载的入射波在终端产生全反射，线上的入射波和反射波相叠加，从而形成了纯驻波状态。

对于任意的电抗性负载都可以用一个有限长的短路线或开路线的输入阻抗来代替。

当传输线终端是短路、开路，或接有纯电抗性(电感性和电容性)负载时。

1-2传输线的总长为5/8λ，终端开路，信号源内阻等于特性阻抗。

终端的电压为15045∠ ，试写出始端、以及与始端相距分别为/8λ和/2λ等处电压瞬时值的表达式。

解：（1） 求终端电压L U终端开路，将产生全反射，线上为纯驻波状态。

终端电压L U 应等于入射电压加反射电压，即+L U U (0)U (0)-=，开路处+U (0)U (0)-=，即L U 2U (0)+=。

而开路线上任一处z 的电压，由下式求出L U z U cos z β()=题中，始端z 5/8λ=处有 0U (z )U (5/8)150/45λ== 故有 0j 45L5150e U c o s ()8βλ=⋅ 即00j45j45j(45)L 150e U 5cos()8πλβ±==-=⋅因此，线上任一处的电压复振幅为0+j (45)LU (z )U c o s z =2U (0)c o 1502c o sz eπβββ±== （2）开路状态下，沿线各处的瞬时电压为j w tu (z ,t )R e [U (z )e1502c o s z c o s (w t 45)βπ==+± 故始端瞬时电压j(45)jwt055u(,cos()e]=100cos zcos(wt+45)88πλλββ±⋅据终端8λ处，则距终端为z2λ=j(45)jwt0u(,)e e)22πλλβ±⋅据终端2λ处，则距终端为z8λ=j(45)jwt0u(,)e e]=150cos(wt+45)88πλλβπ±⋅±1-3传输线的特性阻抗为cZ，行波系数为K，终端负载为LZ，第一个电压最小点距终端的距离为l mi m，试求LZ的表达式。

对于任一集总电路中的任一节点，在任一时刻， 流出（或流入）该节点的所有支路电流的代数和 为零。 由KCL定律， 对于节点1有：
复习：基尔霍夫定律 KVL定律：
对于任一集总电路中的任一回路，在任一时 刻，沿着该回路的所有支路电压降的代数和为 零。 从a点出发，顺时针 方向绕行一周，由KVL定 律有：
传输线的边界条件有：
已知z 0处的终端电压U I 和终端电流I I 已知z l处的始端电压U i和始端电流I i 已知z l处的信源电动势E 和内阻Z 及其负载阻抗Z g g l
讨论第二种情况，已知 z l 处U (l ) U i、I (l ) I i ，则代入上式 U Z 0 I i l 有： A i e U i A1e l A2 e l 1 2 l l U Z I 0 i i e l I i ( A1e A2 e ) / Z 0 A2
行波在传播过程中其幅度按衰减称为衰减常数而相位随连续滞后ingqilu126com11均匀传输线方程及其解传输线的工作特性参数ingqilu126com传输线的工作特性参数特性阻抗z传输线上导行波导行波的电压与电流之比用z表示其倒数称为特性导纳用y特性阻抗是分布参数中用来描述传输线的固有特性的一个物理量频率很低时这种特性显示不出来随着频率升高这种特性才显示出来
基本方程，是描 述传输线的电压、 电流的变化规律 及其相互关系的 微分方程
i ( z, t ) u ( z , t ) Ri ( z, t ) L z t 均匀传输线方程（电报方程） 1-1-3 i ( z, t ) Gu ( z , t ) C u ( z , t ) z t
2 1 E 2 C 满足二维波动方程 2 H 1 C2 2 E 0 t 2 2 H 0 t 2

率的波，而是一个含有多种频率的波。这些多种频率成分构成一个“波群”
又称为波的包络，其传播速度称为群速，用 vg 表示，即 vg v 1 c 2
第三章 微波传输线
TEM波：相速
vp
1 v
相波长
p
2
v f
群速 vg vp v
即导波系统中TEM波的相速等于电磁波在介质中的传播速度，而相波长 等于电磁波在介质中的波长（工作波长）
插入衰减 A
A
1 S21 2
A%11 A%12 A%21 A%22 2 4
对于可逆二端口网络，则有
A
1 S21 2
1 S12 2
第四章 微波网络基础
插入相移 argT arg S21
对于可逆网络，有 S21 S12 T ，故
T T e j S12 e j12 S21 e j21
何不同？
答案：截止波长：对于TEM波，传播常数 为虚数；对于TE波和TM波，对 于一定的 kc 和 、 ，随着频率的变化，传播长数 可能为虚数，也可能为实
数，还可以等于零。当 0 时，系统处于传输与截止状态之间的临界状态，此 时对应的波长为截止波长。
当 c 时，导波系统中传输该种波型。 当 c 时，导波系统中不能传输该种波型。
第三章 微波传输线
3-3 什么是相速、相波长和群速？对于TE波、TM波和TEM波，它们的相速 相波长和群速有何不同？
答案： 相速 vp 是指导波系统中传输的电磁波的等相位面沿轴向移动的速
度，公式表示为
vp
相波长 p
是等相位面在一个周期T内移动的距离，有
p
2
欲使电磁波传输信号，必须对波进行调制，调制后的波不再是单一频
T S21 0.98e j 0.98

§1.3.1 ρ=0、J＝0 的均匀、线性、各向同性、不导电媒质 中：
其中

T
az

z
E

ET
az Ez
H HT az H z
*ET、HT称为电磁场在传输系统中横截面的“分布函 数”（本征函数），并由对偶原理有：


T HT jaz Ez
Z(z)
令
d2 dz 2
Z ( z) / Z ( z ) （ 2
＋j）
T2 E Z (T ) EZ (T )

kc2
有
kc2 k 2 2
解为： Z (z) AeZ AeZ
物理意义：表示沿柱形系统轴向（+Z和-Z方向）传播的 两个行波，即导行波。A+和A-为两个波的振幅；为导 行波的传播常数。则：
Hn S 0 Ht S 0
(6)
n

D
S

S
nB 0
切向电场为零，切向磁场不为零的界 面（电壁）均可视为等效短路面。
S
开路面（理想磁体边界）


n E
S

J mS

nH 0
H t S 0, H n S 0,
En S 0 Et S 0
(7)
采用联立消去法：令 k 2 2 ,
k 2 有：
k称自由空间空间相 位常数。
(k2

2 z 2
)ET

z
T EZ


jaz
T HZ
(k2

2 z 2
)HT

z T H Z

《微波技术》习题解(一、传输线理论)-标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII机械工业出版社《微 波 技 术》（第2版） 董金明 林萍实 邓 晖 编著习 题 解一、 传输线理论1-1 一无耗同轴电缆长10m ，内外导体间的电容为600pF 。

若电缆的一端短路, 另一端接有一脉冲发生器及示波器，测得一个脉冲信号来回一次需0.1s ，求该电缆的特性阻抗Z 0 。

[解] 脉冲信号的传播速度为tlv 2=s /m 102101.010286⨯=⨯⨯=-该电缆的特性阻抗为 00C L Z =00C C L =l C εμ=Cv l=8121021060010⨯⨯⨯=-Ω33.83= 补充题1 写出无耗传输线上电压和电流的瞬时表达式。

[解] (本题应注明z 轴的选法)如图,z 轴的原点选在负载端,指向波源。

根据时谐场传输线方程的通解()()()()()())1()(1..210...21.⎪⎪⎩⎪⎪⎨⎧+=-=+=+=--z I z I e A e A Z z I z U z U e A e A z U r i zj z j r i zj z j ββββ 。

为传输线的特性阻抗式中02.22.1;;,Z U A U A r i ==:(1),,212.2.的瞬时值为得式设ϕϕj r j i e U U eU U -+==⎪⎩⎪⎨⎧+--++=+-+++=-+-+)()cos()cos([1),()()cos()cos(),(21021A z t U z t U Z t z i V z t U z t U t z u ϕβωϕβωϕβωϕβω1-2 均匀无耗传输线，用聚乙烯(εr =2.25)作电介质。

(1) 对Z 0=300 Ω的平行双导线，导线的半径 r =0.6mm ，求线间距D 。

(2) 对Z 0 =75Ω的同轴线，内导体半径 a =0.6mm ，求外导体半径 b 。

i u Ri L z t i Gu C u z t
(2-2)
当典型Δz→0时，有
(2-3)
式(2-3)是均匀传输线方程或电报方程。
2010.9.1
如果我们着重研究时谐(正弦或余弦)的变化情况，有
u( z , t ) Re U ( z )e jt i( z , t ) Re I ( z )e jt
2010.9.1
(1-4)
一、低频传输线和微波传输线
r
r0 r0
图1-2 直线电流均匀分布
图1-3 微波集肤效应
损耗是传输线的重要指标，如果要将r0 R ，使损耗与直 流保持相同，易算出 1 R 3.03 m 2R0 也即直径是d=6.06 m。这种情况，已不能称为微波传输线，而 应称之为微波传输“柱”比较合适，其粗度超过人民大会堂的主 柱。2米高的实心微波传输铜柱约514吨重(铜比重是8.9T/m3)，
同时考虑Ohm定律
V 1 Edl l R0 I Er02 r02 58 10 7 (2 10 3 )2 (1-1) . 137 10 3 / m .
代入铜材料
58 107 .
2010.9.1
一、低频传输线和微波传输线
2. 微波传输线 当频率升高出现的第一个问题是导体的集肤效应 (Skin Effect)。导体的电流、电荷和场都集中在导体表面. ［例2］研究 f=10GHz=1010Hz、l=3cm、r0=2mm导线的线耗R. 这种情况下， J 0 e a ( r0 r ) J 其中, J 0 是r r0 的表面电流密度， 是衰线常数。对于良导 体，由电磁场理论可知



(2-4)

1 1
l l
l=
Zl Z
l
Z0 Z0
|U|max 1|| |U|min 1||
Zl Rl Z0 Zl Rl Z0
R0 Z0
Z0 Rl
15
二、传输线的波类比
1．阻抗变换问题 ［例2］ 典型的两个例子如表所示
C B
A Z 0
1/4g
Z A 2Z0
Z B
Z
2 0
1 2 Z0
l
(1
l
)e
jz '
2lU
l
cos
z'
I ( z' )
I
l
(1
l
)e
jz '
2l
I
l
cos
z'
13
二、传输线的波类比
事实上，上面两种分解都是形式上的。但是有的教材上提及第一项表示行波，第二项 表示(全)驻波。这个概念是完全错误的。先考察分解方法Ⅱ。当Γl=－1(即全驻波情况 下)，第一项所谓“行波”场 。这显然是有问题的。再看分解方法Ⅰ的第一项电压 与电流形成功率
j
1 2
0
ZA
j
j2 1
4
Z0
1
2
上面例子都涉及通过传输线变换，把Zl变成Z０ 这一课题称为匹配（Matching）。
2. 采用网络思想求负载阻抗Zl
17
二、传输线的波类比
I2
et
u1
u2
图 6-4 网络思想
网络思想是一种非常普遍的处理问题方法，它把一线性系统用一个由若干端口对外 的未知网络表示。例如，上图给出两个端口的网络。
画出图来可以明显看出，左边区域的最大场强是

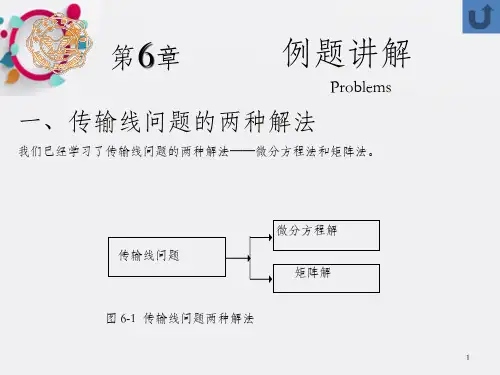
微波技术复习题一、填空题1.若传输线的传播常数γ为复数，则其实部称为衰减常数，量纲为奈培/米(Np/m)或者分贝/米(dB/m)，它主要由导体损耗和介质损耗产生的；虚部称为相位常数，量纲为弧度/米(rad/m)，它体现了微波传输线中的波动过程。

2.微波传输线中相速度是等相位面移动的速度，而群速度则代表能量移动的速度，所以相速度可以大于光速，而群速度只能小于或等于光速，且相速度和群速度的乘积等于光速的平方或c23.在阻抗圆图中，上半圆的阻抗呈感性，下半圆的阻抗呈容性，单位圆上为归一化电阻零，实轴上为归一化电抗零。

4.矩形金属波导(a>b)的主模是TE10，圆形金属波导的主模是TE11，同轴线的主模是TEM。

5.若传输线端接容性负载(ZL =RL+jXL，XL<0)，那么其行驻波分布离负载端最近的是电压节点；若端接感性负载(ZL =RL+jXL，XL>0)，那么其行驻波分布离负载端最近的是电压腹点。

6.阻抗圆图是由单位电压反射系数坐标系和归一化阻抗坐标系组成的，其中前者又由单位电压反射系数的模值圆和单位电压反射系数的相角射线组成，而后者又由归一化电阻圆和归一化电抗圆组成。

7.在金属波导截止的情况下，TE模的波阻抗呈感性，此时磁储能大于(大于/小于)电储能；TM模的波阻抗呈容性，此时电储能大于(大于/小于)磁储能。

8.微带线的主模为准TEM模，这种模式的主要特征是Hz和Ez都不为零，未加屏蔽时，其损耗包括导体损耗，介质损耗和辐射损耗三部分。

9.特性阻抗为50Ω的均匀传输线终端接负载RL为j20Ω,50Ω,20Ω时，传输线上分别形成纯驻波，纯行波，行驻波。

10.均匀传输线的特性阻抗为50Ω，线上工作波长为10cm,终端接有负载ZL，ZLzˊ1).若ZL =50Ω，在zˊ=8cm处的输入阻抗Zin=50Ω, 在zˊ=4cm处的输入阻抗Zin=50Ω。

2).若ZL =0，在zˊ=2.5cm处的输入阻抗Zin=∞Ω, 在zˊ=5cm处的输入阻抗Zin=0Ω,当0<zˊ<2.5cm处, Zin 呈感性，当2.5<zˊ<5cm处, Zin呈容性3). 若ZL=j50Ω，传输线上的驻波系数ρ=∞。

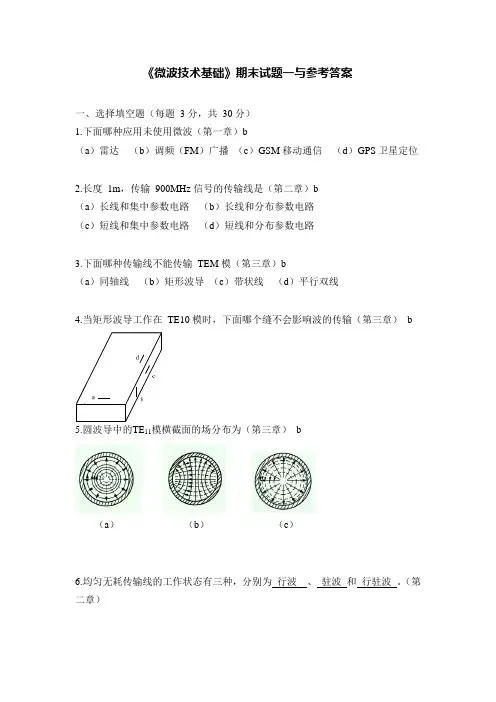
《微波技术基础》期末试题一与参考答案一、选择填空题（每题 3 分，共30 分）1.下面哪种应用未使用微波（第一章）b（a）雷达（b）调频（FM）广播（c）GSM 移动通信（d）GPS 卫星定位2.长度1m，传输900MHz 信号的传输线是（第二章）b（a）长线和集中参数电路（b）长线和分布参数电路（c）短线和集中参数电路（d）短线和分布参数电路3.下面哪种传输线不能传输TEM 模（第三章）b（a）同轴线（b）矩形波导（c）带状线（d）平行双线4.当矩形波导工作在TE10 模时，下面哪个缝不会影响波的传输（第三章）b5.圆波导中的TE11模横截面的场分布为（第三章）b（a）（b）（c）6.均匀无耗传输线的工作状态有三种，分别为行波、驻波和行驻波。

（第二章）Z L 0L 7.耦合微带线中奇模激励的对称面是 电 壁，偶模激励的对称面是 磁 壁。

（第三章）8.表征微波网络的主要工作参量有阻抗参量、 导纳 参量、 传输 参量、散射参量和 转移参量。

9.衰减器有吸收衰减器、 截止衰减器和 极化衰减器三种。

10.微波谐振器基本参量有 谐振波长 、 固有品质因数 和等效电导衰减器三种。

二、传输线理论工作状态（7 分）（第二章）在特性阻抗Z 0=200Ω的传输线上，测得电压驻波比ρ=2，终端为电压波节点，传输线上电压最大值 U max =10V ，求终端反射系数、负载阻抗和负载上消耗的功率。

解： Γ = ρ -1 = 12ρ +1 3由于终端为电压波节点，因此Γ =- 123由Γ =Z L - Z 0= - 12+ Z 3 可得，Z L =100Ω 负载吸收功率为P 2Z 0 ρ三、Smith 圆图（10 分）（第二章）已知传输线特性阻抗Z 0=75Ω，负载阻抗Z L =75+j100Ω，工作频率为 900MHz ，线长l =0.1m ，试用Smith 圆图求距负载最近的电压波腹点与负载的距离和传输线的输入阻抗Z 0Z L解：由工作频率为900 MHz，可得λ=1 m 3而线长为l=0.3λ1.计算归一化负载阻抗ZL=ZLZ= 1+j1.33在阻抗圆图上找到 A 点。

60 r
ln b 43.9 a
当 f 300MHz 时的波长：
1 / 22
p
f
c r
0.67m
1.3 题
设特性阻抗为 Z0 的无耗传输线的驻波比 ，第一个电压波节点离负载的距离为
lmin1 ，试证明此时的终端负载应为
Z1
Z0
1 j tan lmin1 j tan lmin1
证明：
对于无耗传输线而言：
0.33 0.67 j
U (z) U (z) U U (z)1 (z)
U in U ( 8 ) 1 in U1 U (0) 1 1
j
A1e 8 A1e j 0
1 in 1 in
（注意：U (z) 是位置的函数）
U1
U in
1 1 1 in
j
终端反射系数为：1Biblioteka R1 Z 0 R1 Z 0
49 51
0.961
输入反射系数为：
in
1e j2l
49 51
0.961
根据传输线的 4 的阻抗变换性，输入端的阻抗为：
Z in
Z02 R1
2500
1.5 试证明无耗传输线上任意相距λ/4 的两点处的阻抗的乘积等于传输线特性阻抗的平
方。
2 / 22
故可证得传输线上相距的二点处阻抗的乘积等于传输线的特性阻抗。
1.7 求无耗传输线上回波损耗为 3dB 和 10dB 时的驻波比。
解 ：由 Lr 20lg
又由 1 1
当 Lr 3dB 时， 5.85
当 Lr 3dB 时， 1.92
1.9.
特 性 阻 抗 为 Z0 100 , 长 度 为 / 8 的 均 匀 无 耗 传 输 线 , 终 端 接 有 负 载

对于电场线，总是垂直于理想管壁，平行于理想管壁的分量为 对于磁场线，总是平行于理想管壁，垂直于理想管壁的分量为 （ P82）
0 或不存在； 0 或不存在。
2-10. 矩形波导的功率容量与哪些因素有关？ 矩形波导的功率容量与波导横截面的尺寸、模式（或波形） 导中填充介质的击穿强度等因素有关。 （P90）
工作波长 λ，即电磁波在无界媒介中传输时的波长， λ与波导的形状与尺寸无关。 截止波数为传播常数 γ等于 0 时的波数，此时对应的频率称为截止频率，对应的 波长则称为截止波长。它们由波导横截面形状、尺寸，及一定波形等因素决定。 波长只有小于截止波长， 该模式才能在波导中以行波形式传输， 当波长大于截止 波长时，为迅衰场。
2-2. 试从多个方向定性说明为什么空心金属波导中不能传输 TEM模式。※
如果空心金属波导内存在 TEM 波，则要求磁场应完全在波导横截面内，而且是 闭合曲线。 由麦克斯韦第一方程， 闭合曲线上磁场的积分应等于与曲线相交链的 电流。由于空心金属波导中不存在沿波导轴向（即传播方向）的传到电流，所以 要求存在轴向位移电流，这就要求在轴向有电场存在，这与 TEM 波的定义相矛 盾，所以空心金属波导内不能传播 TEM 波。
按损耗特性分类： （ 1）分米波或米波传输线（双导线、同轴线） （ 2）厘米波或分米波传输线（空心金属波导管、带状线、微带线） （ 3）毫米波或亚毫米波传输线（空心金属波导管、介质波导、介质镜像线、微 带线） （ 4）光频波段传输线（介质光波导、光纤）
1-3. 什么是传输线的特性阻抗，它和哪些因素有关？阻抗匹配的物理实质是什 么？
4-5. 微波谐振器的两个主要功能是 储能 和选频 。
4-6. 无耗传输线谐振器串联谐振的条件是 Zin =0，并联谐振的条件是 Zin =∞。

传 输 线 理 论
二、分布参数的概念及传输线的 等效电路
• 电路理论的前提是集中参数，其条件为： •
ι＜＜λ ι：电器尺寸，λ：工作波长 传输线中工作波长和传输长度可比拟，沿 线的电压、电流不仅是时间的函数，还是 空间位置的函数，从而形成分布参数的概 念。
传 输 线 理 论
传输线上处处存在分布电阻、分布电 感，线间处处存在分布电容和漏电导。分 布参数为：R（Ω/m）、L（H/m） C（F/m）、 G（S/m） 如果分布参数沿线均匀，则为均匀传 输线，否则，为非均匀传输线。 传输线的等效电路如图1.1.1所示
EXP：双根传输线
传 输 线 理 论
Zc取决于传输线的几何尺寸和周围媒介， 与传输线的位置和工作频率无关。
传 输 线 理 论
⑶ 相速和波长 相速：某一等相面推进的速度 令α=0（无耗），由ωt-βz=常数,得
传 输 线 理 论
§1-3 反射系数、输入阻抗与 驻波系数
传输线上的电压、电流既然具有波
传 输 线 理 论
第一章 传输线理论
§1-1 传输线的种类及分布 参数的概念
传 输 线 理 论
• 定义：广义上讲，凡是能够导引电磁波
•
沿一定方向传输的导体、介质或由他们 共同组成的导波系统，都可以称为传输 线。 传输线是微波技术中最重要的基本元件 之一，原因有两点： ⑴ 完成把电磁波的能量从一处传到另一 处。 ⑵ 可构成各种用途的微波元件。 Exp：耦合器、匹配器、电容、电感等
传 输 线 理 论
1.3.2式的意义在于： ⑴ 无耗传输线上各点反射系数的大小相等， 均等于终端反射系数的大小。 ⑵ 只要求出|Γ|，若已知λ或β则可求出任意 点的反射系数Γz 随着ZL的性质不同，传输线上将会有 如下不同的工作状：

ln b 43.9 a
当 f 300MHz 时的波长：
p
f
c r
0.67m
1.3 题
设特性阻抗为 Z0 的无耗传输线的驻波比 ，第一个电压波节点离负载的距离为
.
.
lmin1 ，试证明此时的终端负载应为
Z1
Z0
1 j j
t anlmin1 t anlmin1
证明：
对于无耗传输线而言：
Z in（lmin 1）
1.11
设特性阻抗为 Z0 50 的均匀无耗传输线,终端接有负载阻抗 Z1 100 j75 为复
阻抗时,可用以下方法实现λ/4 阻抗变换器匹配：即在终端或在λ/4 阻抗变换器前并接一段
终端短路线, 如题 1.11 图所示, 试分别求这两种情况下λ/4 阻抗变换器的特性阻抗 Z01 及短
路线长度 l。 （最简便的方式是:归一化后采用 Smith 圆图计算）
1 e j0.8 3
(0.5) 1 （二分之一波长重复性） 3
(0.25) 1 3
Zin (0.2 )
Z0
Z1 Z0
jZ0 jZ1
t an l t an l
29.43
2 3.7 9
Zin(0.25) 502 /100 25 （四分之一波长阻抗变换性）
Zin(0.5) 100
（二分之一波长重复性）
令并联短路线和负载并联后的输入阻抗为 Z 2 .
Z 2 =1/ Re[Y1] 156 则 Z 01 Z0Z2 =88.38
(2)
令 4
特性阻抗为 Z 01 ，并联短路线长为 l
Z in2 Z01
Z1 Z01 j t an Z01 Z1 j t an
4

微波技术习题解答第1章练习题1.1 无耗传输线的特性阻抗Z0= 100()。

根据给出的已知数据，分别写出传输线上电压、电流的复数和瞬时形式的表达式：(1) R L= 100 ()，I L = e j0(mA)；(2) R L = 50()，V L = 100e j0(mV)；(3) V L = 200e j0 (mV)，I L = 0(mA)。

解：本题应用到下列公式：(1)(2)(3)(1) 根据已知条件，可得：V L = I L R L = 100(mV)，复数表达式为：瞬时表达式为：(2) 根据已知条件，可得：复数表达式为：瞬时表达式为：(3) 根据已知条件，可得：复数表达式为：瞬时表达式为：1.2 无耗传输线的特性阻抗Z0 = 100()，负载电流I L = j(A)，负载阻抗Z L = j100()。

试求：(1) 把传输线上的电压V(z)、电流I(z)写成入射波与反射波之和的形式；(2) 利用欧拉公式改写成纯驻波的形式。

解：根据已知条件，可得：V L = I L Z L = j(j100) = 100(V)，1.3 无耗传输线的特性阻抗Z0 = 75()，传输线上电压、电流分布表达式分别为试求：(1) 利用欧拉公式把电压、电流分布表达式改写成入射波与反射波之和的形式；(2) 计算负载电压V L、电流I L和阻抗Z L；(3) 把(1)的结果改写成瞬时值形式。

解：根据已知条件求负载电压和电流：电压入射波和反射波的复振幅为(1) 入射波与反射波之和形式的电压、电流分布表达式(2) 负载电压、电流和阻抗V L = V(0) = 150j75，I L = I(0) = 2 + j(3) 瞬时值形式的电压、电流分布表达式1.4 无耗传输线特性阻抗Z0 = 50()，已知在距离负载z1= p/8处的反射系数为 (z1)= j0.5。

试求(1) 传输线上任意观察点z处的反射系数(z)和等效阻抗Z(z)；(2) 利用负载反射系数 L计算负载阻抗Z L；(3) 通过等效阻抗Z(z)计算负载阻抗Z L。

机械工业出版社《微 波 技 术》（第2版） 董金明 林萍实 邓 晖 编著习 题 解一、 传输线理论1-1 一无耗同轴电缆长10m ，内外导体间的电容为600pF 。

若电缆的一端短路, 另一端接有一脉冲发生器及示波器，测得一个脉冲信号来回一次需0.1μs ，求该电缆的特性阻抗Z 0 。

[解] 脉冲信号的传播速度为t l v 2=s /m 102101.010286⨯=⨯⨯=-该电缆的特性阻抗为0C L Z =00C C L =l C εμ=Cv l =8121021060010⨯⨯⨯=-Ω33.83= 补充题1 写出无耗传输线上电压和电流的瞬时表达式。

[解] (本题应注明z 轴的选法)如图,z 轴的原点选在负载端,指向波源。

根据时谐场传输线方程的通解()()()()()())1()(1..210...21.⎪⎪⎩⎪⎪⎨⎧+=-=+=+=--z I z I e A e A Z z I z U z U e A e A z U r i zj z j r i zj z j ββββ。

为传输线的特性阻抗式中02.22.1;;,Z U A U A r i ==:(1),,212.2.的瞬时值为得式设ϕϕj r j i e U U eU U -+==⎪⎩⎪⎨⎧+--++=+-+++=-+-+)()cos()cos([1),()()cos()cos(),(21021A z t U z t U Z t z i V z t U z t U t z u ϕβωϕβωϕβωϕβω1-2 均匀无耗传输线，用聚乙烯(εr =2.25)作电介质。

(1) 对Z 0=300 Ω的平行双导线，导线的半径 r =0.6mm ，求线间距D 。

(2) 对Z 0 =75Ω的同轴线，内导体半径 a =0.6mm ，求外导体半径 b 。

[解] (1) 对于平行双导线(讲义p15式(2-6b ))0C L Z =rD r D ln ln πεπμ=r D ln 1εμπ=r Drln 120ε=300= Ω 得52.42=rD, 即 mm 5.256.052.42=⨯=D (2) 对于同轴线(讲义p15式(2-6c )) Z L补充题1图示Z g e (t ) 题1-4图示 00C L Z =dD d D ln 2ln2πεπμ=d D r ln 60ε=ab r ln 60ε=75= Ω 得52.6=ab, 即 mm 91.36.052.6=⨯=b 1-3 如题图1-3所示,已知Z 0=100Ω, Z L =Z 0 ,又知负载处的电压瞬时值为u 0 (t)=10sin ωt (V), 试求: S 1 、S 2 、S 3 处电压和电流的瞬时值。