C
A
D
切线的性质定理是证明两线垂直的重要根据;作
过切点的半径是常用经验辅助线之一.
直线何时变为切线
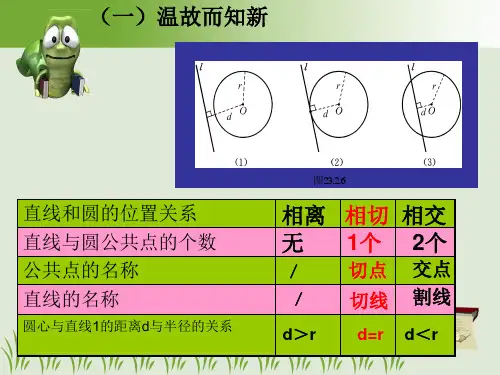
如图,AB是⊙O的直径,直线CD经过点A,CD与AB的夹角
为∠α,当CD绕点A旋转时,
B
1.随着∠α的变化,点O到CD的距离
如何变化?直线CD与⊙O的位置关系
如何变化?
●O
2.当∠α等于多少度时,点O到CD 的距离等于半径?此时,直线CD与 ⊙O有的位置关系?有为什么?
B
┓
C
∴因此和△ABC三边都相切的圆可以作出一个, 并且只能作一个.
三角形与圆的位置关系
这圆叫做三角形的内切圆.这个
A
三角形叫做圆的外切三角形.
内切圆的圆心是三角形三
条角平分线的交点,叫做三
角形的内心.
B
I
●
C
老师提示: 多边形的边与圆的位置关系称为切.
四边形与圆的位置关系
如果四边形的四条边都与一个圆 A 相切,这圆叫做四边形的内切圆. 这个四边形叫做圆的外切四边形.
相切?
A
A
I
I
●●●●B┓CB┓
C
老师提示:
假设符合条件的圆已作出,则它的圆心到三边的距离 相等.因此,圆心在这个三角形三个角的平分线上,半径
为圆心到三边的距离.
三角形与圆的位置关系
这样的圆可以作出几个?为什么?. A
∵直线BE和CF只有一个交点I, F
E
并且点I到△ABC三边的距离相
I
●●
等(为什么?),
老师提示: 先确定圆心和半径,尺规作图要保留作图痕迹.
挑战自我
驶向胜利 的彼岸
习题3.8 1,2题