clementine 回归分析Regression_association

C&R tree的案例应用——Clementine应用C&R tree全程为the classification and regression tree，分类回归树是是一种基于树的分类和预测方法，模型使用简单，易于理解（规则解释起来更简明易），该方法通过在每个步骤最大限度降低不纯洁度，使用递归分区来将训练记录分割为组。

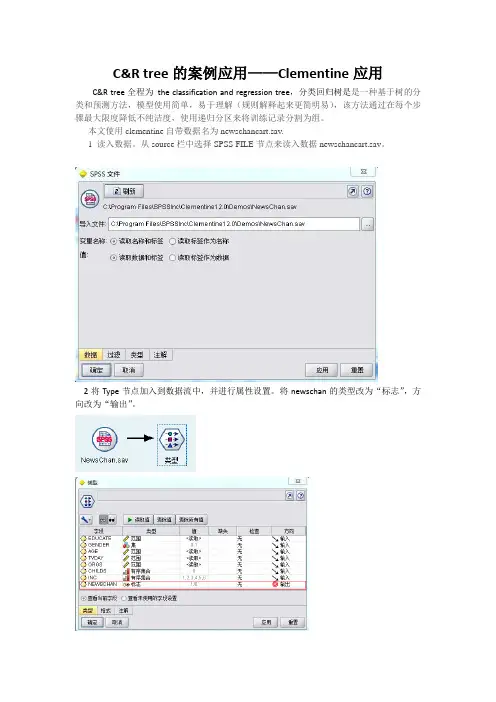
本文使用clementine自带数据名为newschancart.sav.1 读入数据。

从source栏中选择SPSS FILE节点来读入数据newschancart.sav。

2将Type节点加入到数据流中，并进行属性设置。

将newschan的类型改为“标志”，方向改为“输出”。

3 加入C-R tree 节点，在模型设置中选择“启动交互会话”，此功能是在节点被执行之后，在树生成模型前可以对树进行编辑。

在“专家”栏中，选择专家模式，使用标准误差规则，将最小杂质改变值设为0.003，这个设置可以形成一个比较简单的树模型。

在停止标准中使用绝对值，父分支中和子分支中的最小记录分别为25，10。

4 运行此模型。

从图中结果可以发现训练数据一共有442个记录，其中215个数据回应为yes，占有约49%。

5下面让我们利用树模型看看能否改善这种积极的回应。

选择“生长树并修建”选项，结果如下：在图中我们发现，在关于年龄的第二个节点中，yes的积极回应率增加到68%左右，此时年龄大于40.5。

而年龄在小于或等于40.5的节点1具有较低的回应率仅为34.5%，继续向下面的节点看，即使在节点1之后的分类中，也有偏高的回应率如节点13的回应率为60.4%。

6 检查树的收益表。

收益指数能够有助于划分每一个节点的目标类别的比例。

选择目标类别为1。

如下图：图中所示，节点2和节点13具有最高指数，节点2的指数高达140%，这说明这类群体积极接受的机会是1.4倍。

7 在分位数中选择十分位数，以图表展示提升，目标类别依旧为1。

实验一Clementine12.0数据挖掘分析方法与应用一、[实验目的]熟悉Clementine12.0进行数据挖掘的基本操作方法与流程，对实际的问题能熟练利用Clementine12.0开展数据挖掘分析工作。

二、[知识要点]1、数据挖掘概念；2、数据挖掘流程；3、Clementine12.0进行数据挖掘的基本操作方法。

三、[实验内容与要求]1、熟悉Clementine12.0操作界面；2、理解工作流的模型构建方法；3、安装、运行Clementine12.0软件；4、构建挖掘流。

四、[实验条件]Clementine12.0软件。

五、[实验步骤]1、主要数据挖掘模式分析；2、数据挖掘流程分析；3、Clementine12.0下载与安装；4、Clementine12.0功能分析；5、Clementine12.0决策分析实例。

六、[思考与练习]1、Clementine12.0软件进行数据挖掘的主要特点是什么？2、利用Clementine12.0构建一个关联挖掘流（购物篮分析）。

实验部分一、Clementine简述Clementine是ISL(Integral Solutions Limited)公司开发的数据挖掘工具平台。

1999年SPSS公司收购了ISL公司，对Clementine产品进行重新整合和开发，现在Clementine已经成为SPSS公司的又一亮点。

作为一个数据挖掘平台，Clementine结合商业技术可以快速建立预测性模型，进而应用到商业活动中，帮助人们改进决策过程。

强大的数据挖掘功能和显著的投资回报率使得Clementine在业界久负盛誉。

同那些仅仅着重于模型的外在表现而忽略了数据挖掘在整个业务流程中的应用价值的其它数据挖掘工具相比，Clementine其功能强大的数据挖掘算法，使数据挖掘贯穿业务流程的始终，在缩短投资回报周期的同时极大提高了投资回报率。

为了解决各种商务问题，企业需要以不同的方式来处理各种类型迥异的数据，相异的任务类型和数据类型就要求有不同的分析技术。

各种线性回归模型原理线性回归是一种广泛应用于统计学和机器学习领域的方法，用于建立自变量和因变量之间线性关系的模型。

在这里，我将介绍一些常见的线性回归模型及其原理。

1. 简单线性回归模型（Simple Linear Regression）简单线性回归模型是最简单的线性回归模型，用来描述一个自变量和一个因变量之间的线性关系。

模型方程为：Y=α+βX+ε其中，Y是因变量，X是自变量，α是截距，β是斜率，ε是误差。

模型的目标是找到最优的α和β，使得模型的残差平方和最小。

这可以通过最小二乘法来实现，即求解最小化残差平方和的估计值。

2. 多元线性回归模型（Multiple Linear Regression）多元线性回归模型是简单线性回归模型的扩展，用来描述多个自变量和一个因变量之间的线性关系。

模型方程为：Y=α+β1X1+β2X2+...+βnXn+ε其中，Y是因变量，X1,X2,...,Xn是自变量，α是截距，β1,β2,...,βn是自变量的系数，ε是误差。

多元线性回归模型的参数估计同样可以通过最小二乘法来实现，找到使残差平方和最小的系数估计值。

3. 岭回归（Ridge Regression）岭回归是一种用于处理多重共线性问题的线性回归方法。

在多元线性回归中，如果自变量之间存在高度相关性，会导致参数估计不稳定性。

岭回归加入一个正则化项，通过调节正则化参数λ来调整模型的复杂度，从而降低模型的过拟合风险。

模型方程为：Y=α+β1X1+β2X2+...+βnXn+ε+λ∑βi^2其中，λ是正则化参数，∑βi^2是所有参数的平方和。

岭回归通过最小化残差平方和和正则化项之和来估计参数。

当λ=0时，岭回归变为多元线性回归，当λ→∞时，参数估计值将趋近于0。

4. Lasso回归（Lasso Regression）Lasso回归是另一种用于处理多重共线性问题的线性回归方法，与岭回归不同的是，Lasso回归使用L1正则化，可以使得一些参数估计为0，从而实现特征选择。

基于clementine的数据挖掘实验指导目录clementine决策树分类模型 (2)一．基于决策树模型进行分类的基本原理概念 (2)二. 范例说明 (2)三. 数据集说明 (3)四. 训练模型 (3)五. 测试模型 (7)clementine线性回归模型 (10)一. 回归分析的基本原理 (10)二. 范例说明 (10)三. 数据集说明 (10)四. 训练模型 (10)五. 测试模型 (15)Clementine聚类分析模型 (18)一. 聚类分析的基本原理 (18)二. 范例说明 (18)三. 数据集说明 (18)四. 建立聚类模型 (19)Clementine关联规则模型 (24)一. 关联规则的基本原理 (24)二. 范例说明 (24)三. 数据集说明 (25)四. 关联规则模型 (25)clementine决策树分类模型一．基于决策树模型进行分类的基本原理概念分类就是：分析输入数据，通过在训练集中的数据表现出来的特性，为每一个类找到一种准确的描述或者模型。

由此生成的类描述用来对未来的测试数据进行分类。

数据分类是一个两步过程:第一步，建立一个模型,描述预定的数据类集或概念集；第二步，使用模型进行分类。

clementine 8.1中提供的回归方法有两种：C5.0（C5.0决策树）和Neural Net（神经网络）。

下面的例子主要基于C5.0决策树生成算法进行分类。

C5.0算法最早(20世纪50年代)的算法是亨特CLS(Concept Learning System)提出，后经发展由J R Quinlan在1979年提出了著名的ID3算法，主要针对离散型属性数据；C4.5是ID3后来的改进算法，它在ID3基础上增加了：对连续属性的离散化；C5.0是C4.5应用于大数据集上的分类算法，主要在执行效率和内存使用方面进行了改进。

优点：在面对数据遗漏和输入字段很多的问题时非常稳健；通常不需要很长的训练次数进行估计；比一些其他类型的模型易于理解，模型推出的规则有非常直观的解释；也提供强大的增强技术以提高分类的精度。

35种原点回归模式详解在数据分析与机器学习的领域中，回归分析是一种重要的统计方法，用于研究因变量与自变量之间的关系。

以下是35种常见的回归分析方法，包括线性回归、多项式回归、逻辑回归等。

1.线性回归（Linear Regression）：最简单且最常用的回归分析方法，适用于因变量与自变量之间存在线性关系的情况。

2.多项式回归（Polynomial Regression）：通过引入多项式函数来扩展线性回归模型，以适应非线性关系。

3.逻辑回归（Logistic Regression）：用于二元分类问题的回归分析方法，其因变量是二元的逻辑函数。

4.岭回归（Ridge Regression）：通过增加一个正则化项来防止过拟合，有助于提高模型的泛化能力。

5.主成分回归（Principal Component Regression）：利用主成分分析降维后进行线性回归，减少数据的复杂性。

6.套索回归（Lasso Regression）：通过引入L1正则化，强制某些系数为零，从而实现特征选择。

7.弹性网回归（ElasticNet Regression）：结合了L1和L2正则化，以同时实现特征选择和防止过拟合。

8.多任务学习回归（Multi-task Learning Regression）：将多个任务共享部分特征，以提高预测性能和泛化能力。

9.时间序列回归（Time Series Regression）：专门针对时间序列数据设计的回归模型，考虑了时间依赖性和滞后效应。

10.支持向量回归（Support Vector Regression）：利用支持向量机技术构建的回归模型，适用于小样本数据集。

11.K均值聚类回归（K-means Clustering Regression）：将聚类算法与回归分析相结合，通过对数据进行聚类后再进行回归预测。

12.高斯过程回归（Gaussian Process Regression）：基于高斯过程的非参数贝叶斯方法，适用于解决非线性回归问题。

回归分析回归分析（Regression Analysis ）是研究因变量y 和自变量x 之间数量变化规律，并通过一定的数学表达式来描述这种关系，进而确定一个或几个自变量的变化对因变量的影响程度。

简约地讲，可以理解为用一种确定的函数关系去近似代替比较复杂的相关关系，这个函数称为回归函数，在实际问题中称为经验公式。

回归分析所研究的主要问题就是如何利用变量X ，Y 的观察值（样本），对回归函数进行统计推断，包括对它进行估计及检验与它有关的假设等。

在SPSS 中的“Analyze ”菜单下的“Regression ”项是专门用于回归分析的过程组。

单击该项，将打开“Regression ”的右拉式菜单，菜单包含如下几项：1.Linear 线性回归。

2.Curve Estimation 曲线估计。

3.Binary Logistic 二元逻辑分析。

4.Multinomial Logistic 多元逻辑分析。

5.Ordinal 序数分析。

6.Probit 概率分析。

7.Nonlinear 非线性估计。

8.Weight Estimation 加权估计。

9.2-Stage Least Squares 两段最小二乘法。

本课程将介绍其中的“Linear ”、“Curve Estimation ”和“Nonlinear ”项过程的应用。

一元回归分析在数学关系式中只描述了一个变量与另一个变量之间的数量变化关系，则称其为一元回归分析。

其回归模型为i i i bx a y ε++=，y 称为因变量，x 称为自变量，ε称为随机误差，a ,b 称为待估计的回归参数，下标i 表示第i 个观测值。

若给出a 和b 的估计量分别为b aˆ,ˆ则经验回归方程：ii x b a y ˆˆˆ+=，一般把i i i y y e ˆ-=称为残差， 残差i e 可视为扰动ε的“估计量”。

例：湖北省汉阳县历年越冬代二化螟发蛾盛期与当年三月上旬平均气温的数据如表1-1，分析三月上旬平均温度与越冬代二化螟发蛾盛期的关系。

你应该要掌握的7种回归分析方法回归分析是一种常用的数据分析方法，用于研究自变量与因变量之间的关系。

在实际应用中，有许多不同的回归分析方法可供选择。

以下是应该掌握的7种回归分析方法：1. 简单线性回归分析(Simple Linear Regression)：简单线性回归是回归分析中最简单的方法之一、它是一种用于研究两个变量之间关系的方法，其中一个变量是自变量，另一个变量是因变量。

简单线性回归可以用来预测因变量的值，基于自变量的值。

2. 多元线性回归分析(Multiple Linear Regression)：多元线性回归是在简单线性回归的基础上发展起来的一种方法。

它可以用来研究多个自变量与一个因变量之间的关系。

多元线性回归分析可以帮助我们确定哪些自变量对于因变量的解释最为重要。

3. 逻辑回归(Logistic Regression)：逻辑回归是一种用于预测二分类变量的回归分析方法。

逻辑回归可以用来预测一个事件发生的概率。

它的输出是一个介于0和1之间的概率值，可以使用阈值来进行分类。

4. 多项式回归(Polynomial Regression)：多项式回归是回归分析的一种扩展方法。

它可以用来研究变量之间的非线性关系。

多项式回归可以将自变量的幂次作为额外的变量添加到回归模型中。

5. 岭回归(Ridge Regression)：岭回归是一种用于处理多重共线性问题的回归分析方法。

多重共线性是指自变量之间存在高度相关性的情况。

岭回归通过对回归系数进行惩罚来减少共线性的影响。

6. Lasso回归(Lasso Regression)：Lasso回归是另一种可以处理多重共线性问题的回归分析方法。

与岭回归不同的是，Lasso回归通过对回归系数进行惩罚，并使用L1正则化来选择最重要的自变量。

7. Elastic Net回归(Elastic Net Regression)：Elastic Net回归是岭回归和Lasso回归的结合方法。

罗吉斯回归统计分析上常使用回归分析来探讨应变量与自变量间的关系，但线性回归分析只是用于因变量为连续变量的情形，而当因变量是离散变量的时候，应使用logistic 回归分析。

Logistic 回归模型采用罗吉斯变换将离散的因变量变量转化为实数轴上的连续机会比变量，并通过极大似然法来估计模型的参数。

二元（布尔型变量flag ） 线性回归分析 罗吉斯回归分析（应变量的取值预测） （目标变量是否发 多元（有序集order set ）生的概率P 预测）1 因变量的罗吉斯变换变换的目的：将线性关系转化为可描述的非线性关系；将目标变量是否发生的概率P 的取值范围（0,1）转化到（-∞，+∞）；且变换要保持单调性不便变换步骤：Step1：P()()x 1-P x ⎛Ω=⎜⎝⎠⎞⎟称其为“相对风险比”odds ，(0,)Ω∈+∞Step2：P()()()x Y log log 1-P x ⎛⎞=Ω=⎜⎟⎝⎠这样就可以对Y 进行回归分析：p p 110x β...x ββY +++= ①Step1与Step2统称Logit 变换，回归方程又可表示为011...p p LogitP x x βββ=+++方程中因变量是“相对风险比”（odds ）的对数，机会比指的是选择1的机会与选择0的机会1-之比。

如果正好取0或者1的时候，机会比就会等于0或者没意义，此时若采用普通最小二乘法就不合适，且因为logistic 回归跟概率的关系密切，所以通常采用极大似然估计对方程 ①进行估计。

()P x ()P x ()P x2 极大似然估计MLE极大似然估计方法是求估计的用得最多的方法,1821年首先由德国数学家C. F. Gauss 提出，但是这个方法通常被归功于英国的统计学家R. A. Fisher ，他在1922年再次提出了这个思想，并且首先探讨了这种方法的一些性质，从而使得极大似然法得到广泛的应用。

它是建立在极大似然原理的基础上的一个统计方法，极大似然原理的直观想法是：一个随机试验如有若干个可能的结果A ，B ，C ，…。

Clementine⼆项Logistic回归熟悉统计的同学对回归肯定不陌⽣。

前⾯我们介绍正态分布（Normal Distribution）的时候也多少提到过回归。

事实上，回归这⼀概念最早是在19世纪7、80年华由著名的⽣物统计学家⾼尔顿（著名⽣物学家达尔⽂的表弟，⼀译⾼尔登）提出来的。

⾼尔顿在研究遗传现象时，发现母体偏⾼的⼦代有趋于普通⾼度的趋势；母体偏矮的⼦代有也有趋于普通⾼度的趋势。

因此，⾼尔顿发现⼦代都有回归到普通⽔平的趋势。

回归的提出，是统计学由描述性统计学阶断过渡到推断性统计阶断的标志之⼀。

因此我们利⽤回归技术就能实现对未来的“预测”，这在统计学史上是⼀次巨⼤的飞跃。

常见的简单线性回归能进⾏⼀般数值的预测，本⽂要介绍的Logistic回归则是对类别的推断。

当⽬标变量含有两个选项（即我们常提到的⼆分问题）时，我们可以使⽤⼆项Logistic回归；当⽬标变量含有多个选项时，我们则可以使⽤多项Logistic回归。

本案例假设的情景如下：假设某个电信服务提供商⾮常关⼼流失到竞争对⼿那⾥的客户数。

如果可以使⽤服务使⽤数据预测有可能转移到其他提供商的客户，则可通过定制服务使⽤数据来尽可能多地保留这些客户。

也就是我们常说的电信客户流失模型。

⾸先导⼊源数据。

源—Spss⽂件，我们导⼊所需要的数据Telo.sav，添加“类型”节点，在“类型”节点⾥，我们可以根据实际情况更改数据的类型。

由0和1构成的数据⼀般是标志型数据，然后将⽬标变量churn的字段⽅向设置为“输出”，其它字段的⽅向设置为输⼊，这样我们就能通过其它字段来对⽬标变量Churn进⾏预测了。

际情况中，我们往往⽆法在事先就确知哪些测量字段对预测有意义，哪些没有意义。

哪么，我们能不能把那些重要的——即具有特征性的——变量筛选出来呢？继续添加“特征选择”节点，在“特征选择”节点的对话框中保持默认状态，点击执⾏。

然后浏览⽣成的模型。

我们发现系统帮助我们筛选出了三个不适合的字希，原因为单个类别过⼤、缺失值过多和变异系数低于阈值。

4、神经网络（goodlearn.str）神经网络是一种仿生物学技术，通过建立不同类型的神经网络可以对数据进行预存、分类等操作。

示例goodlearn.str通过对促销前后商品销售收入的比较，判断促销手段是否对增加商品收益有关。

Clementine提供了多种预测模型，包括Nerual Net、Regression和Logistic。

这里我们用神经网络结点建模，评价该模型的优良以及对新的促销方案进行评估。

Step一：读入数据，本示例的数据文件保存为GOODS1n，我们向数据流程区添加Var.File结点，并将数据文件读入该结点。

Step二、计算促销前后销售额的变化率向数据流增加一个Derive结点，将该结点命名为Increase。

在公式栏中输入(After-Before)/Before*100.0以此来计算促销前后销售额的变化Step三：为数据设置字段格式添加一个Type结点到数据流中。

由于在制定促销方案前我们并不知道促销后商品的销售额，所以将字段After的Direction属性设置为None；神经网络模型需要一个输出，这里我们将Increase字段的Direction设置为Out，除此之外的其它结点全设置为In。

Step四：神经网络学习过程在设置好各个字段的Direction方向后我们将Neural Net结点连接入数据流。

在对Neural Net进行设置时我们选择快速建模方法（Quick），选中防止过度训练(Prevent overtraining)。

同时我们还可以根据自己的需要设置训练停止的条件。

在建立好神经网络学习模型后我们运行这条数据流，结果将在管理器的Models栏中显示。

选择查看该结果结点，我们可以对生成的神经网络各个方面的属性有所了解。

Step四：为训练网络建立评估模型4.1将模型结果结点连接在数据流中的Type结点后；4.2添加字段比较预测值与实际值向数据流中增加Derive结点并将它命名为ratio，然后将它连接到Increase结果结点。