下载文档原格式
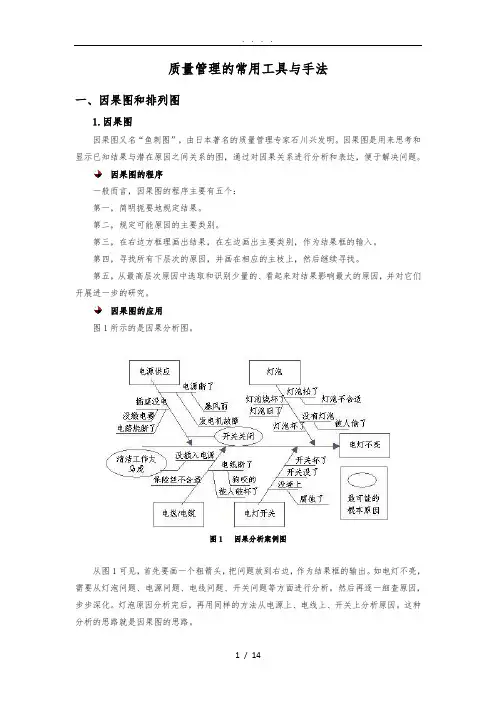
质量管理的常用工具与手法一、因果图和排列图1.因果图因果图又名“鱼刺图”，由日本著名的质量管理专家石川兴发明。
因果图是用来思考和显示已知结果与潜在原因之间关系的图，通过对因果关系进行分析和表达，便于解决问题。
因果图的程序一般而言，因果图的程序主要有五个：第一，简明扼要地规定结果。
第二，规定可能原因的主要类别。
第三，在右边方框理画出结果，在左边画出主要类别，作为结果框的输入。
第四，寻找所有下层次的原因，并画在相应的主枝上，然后继续寻找。
第五，从最高层次原因中选取和识别少量的、看起来对结果影响最大的原因，并对它们开展进一步的研究。
因果图的应用图1所示的是因果分析图。
图1 因果分析案例图从图1可见，首先要画一个粗箭头，把问题放到右边，作为结果框的输出。
如电灯不亮，需要从灯泡问题、电源问题、电线问题、开关问题等方面进行分析。
然后再逐一细查原因，步步深化。
灯泡原因分析完后，再用同样的方法从电源上、电线上、开关上分析原因。
这种分析的思路就是因果图的思路。
2.排列图排列图又名排队图，是为了对最主要到最次要的项目进行排列而作出的简单图示。
排列图的作用一般而言，排列图主要有三个用途：第一，按重要性顺序显示出每个项目对整个问题的作用。
第二，提出识别改进的机会。
第三，用最小的努力获得最大的成功。
排列图的应用[案例]快速热水器的排列图2000年，某热水器厂商开发出了一种快速热水器产品，这种热水器打开5秒钟后，就能完成将水加热，而且可以持续24小时源源不断地供应热水。
但在试验过程中，出现了一个问题，即关键发热零件有时会突然烧掉。
要查出上述问题的原因，可以用排列图表进行分析。
表1 排列图分析表名称频数累计频数累计频率拉弧25125176.9%功率不合格3728888.3%掉膜1630493.3%端面不平1031496.3%其他12326从表1可见，首先，统计最近发生的所有问题，统计出各种制品中的共326个残缺品；其次，再逐项进行分类，例如拉弧一项就占了251个，功率不合格的占了37个，发热膜脱落的有16个，端面不平有10个，还有12个是由于其他原因。
质量管理的数学原理质量管理是一种通过采取措施和方法来确保产品和服务满足顾客需求的过程。
在质量管理中，数学原理被广泛应用，它们为质量管理提供了理论基础和实践指导。
本文将介绍质量管理中一些重要的数学原理，并讨论它们在实际应用中的作用。
1. 统计学原理统计学是质量管理中最常用的数学工具之一。
它通过收集和分析数据来评估和改进过程的性能。
统计学原理包括描述性统计、概率论、抽样理论、假设检验和方差分析等。
这些原理可以帮助质量管理人员了解过程的变异性，并作出合理的决策。
2. 六西格玛原理六西格玛是一种以统计学为基础的质量管理方法。
它通过减少过程的变异性来提高质量水平。
六西格玛原理基于统计学的标准差概念，通过测量和分析过程的性能，确定并消除造成质量问题的根本原因。
通过应用六西格玛原理，组织可以实现质量的持续改进。
3. 控制图原理控制图是一种用于监控过程性能的图表工具。
它基于统计学原理，通过绘制过程数据的变化趋势，帮助质量管理人员判断过程是否处于控制状态。
控制图原理可以帮助质量管理人员及时发现和纠正过程中的异常，确保产品和服务的稳定性和可靠性。
4. 因果图原理因果图是一种用于分析问题根本原因的图表工具。
它基于因果关系的概念，帮助质量管理人员确定问题的根本原因，并制定相应的改进措施。
因果图原理可以帮助质量管理人员系统地分析和解决复杂的质量问题，提高质量管理的效果。
5. 算法原理算法是质量管理中常用的数学工具之一。
它通过定义一系列步骤和规则，帮助质量管理人员解决特定的问题。
算法原理可以帮助质量管理人员设计和实施有效的质量管理过程，提高工作效率和质量水平。
6. 概率原理概率是质量管理中重要的数学概念之一。
它用于描述事件发生的可能性，并帮助质量管理人员评估和控制风险。
概率原理可以帮助质量管理人员制定合理的决策和计划，提高质量管理的可靠性和可预测性。
7. 线性规划原理线性规划是一种用于优化问题的数学方法。
在质量管理中，线性规划原理可以帮助质量管理人员确定最佳的资源分配方案，以实现质量和成本的最优平衡。
管理的数学方法与工具食品质量管理数学在食品质量管理中起到了重要的作用，它为管理者提供了许多方法和工具，帮助他们更好地分析和解决问题，提高食品质量管理水平。
首先，数学在统计分析方面发挥了重要作用。
食品质量管理需要对大量的数据进行分析和处理，以了解产品的质量水平、生产过程中的潜在问题等。
常用的统计方法包括均值、标准差、方差等，它们可以帮助管理者了解产品的分布情况和变异程度，进而制定相应的控制策略。
此外，还可以利用统计方法进行假设检验，判断质量控制措施的有效性，以及对各种因素对食品质量的影响进行分析，为提高食品质量提供依据。
其次，数学在食品质量控制中的模型建立和优化方面也发挥了重要作用。
数学建模是将实际问题抽象化、数学化的过程，可以帮助管理者找到问题的本质和规律，从而制定科学合理的管理方案。
在食品质量管理中，可以利用统计模型来描述产品的质量特性，如正态分布模型、指数分布模型等，以及回归模型来研究各种因素对产品质量的影响，进而制定相应的控制策略。
此外，还可以利用优化方法来优化生产过程，最大程度地提高产品的质量，如线性规划、动态规划等。
另外，数学在食品质量管理中的决策分析方面也起到了关键作用。
在管理过程中，管理者需要根据各种因素和目标制定决策方案，通过数学模型和方法，可以对不同的决策方案进行评估和比较，帮助管理者做出正确的决策。
比如，在供应链管理中，可以利用数学方法建立供应链模型，分析不同决策方案对供应链效益的影响，帮助管理者选择最佳的供应链策略。
此外，还可以利用风险分析方法，对食品安全风险进行评估和管理，提高食品质量的安全性。
此外，数学在食品质量管理中的标准制定方面也起到了重要作用。
食品质量管理需要依据一定的标准和指标来进行评估和比较，从而确定产品的质量水平。
数学可以帮助管理者建立标准和指标体系，确定评价指标的权重，以及制定评价方法和标准化的流程，从而实现对食品质量的科学评估和管理。
总之，数学在食品质量管理中的方法和工具是多种多样的，包括统计分析、模型建立和优化、决策分析、标准制定等。
