数学三角函数与圆初三

2011 中考数学复习专题—三角函数和圆考点 1三角形的边角关系主要考查：三种锐角三角函数的概念，特殊值计算，锐角函数之间的关系，解直角三角形及应用。

1. 如图所示， Rt △ ABC～ Rt △ DEF，则 cosE 的值等于（）A ．1B．2C．3D．3 22232. 如图，已知直角三角形ABC中，斜边 AB的长为 m，∠B=40，则直角边 BC的长是（）A．msin 40B． mcos 40C ． mtan40D．mtan 403. 王师傅在楼顶上的点 A 处测得楼前一棵树CD 的顶端 C 的俯角为 60，又知水平距离BD=10m，楼高 AB=24m，则树高 CD为（）A ． 24 10 3 m B．2410 3 m C ． 24 5 3 m D．9m34. 如图是掌上电脑设计用电来测量某古城墙高度的示意图。

点P 处放一水平的平面镜，光线从点 A出发经平面镜反射后刚好射到古城墙CD的顶端 C 处，已知 AB⊥ BD， CD⊥BD，且测得 AB=1.2 米， BP=1.8 米， PD=12 米，那么该古城墙的高度是（）A ． 6 米B． 8 米C． 18 米D． 24 米5.如图所示，某河堤的横断面是梯形 ABCD，BC∥ AD，迎水坡 AB长 13 米，且 tan ∠ BAE=12，5 则河堤的高 BE为米。

6．如果，小明同学在东西方向的环海路 A 处，测得海中灯塔P 在北偏东 60 方向上，在A 处东 500 米的 B 处，测得海中灯塔P 在北偏东 30 方向上，则灯塔 P到环海路的距离PC=米（用根号表示）。

7．某大草原上有一条笔直的公路，在紧靠公路相距40 千米的 A、 B 两地，分别有甲、乙两个医疗站，如图，在 A 地北偏东 45 、B 地北偏西 60方向上有一牧民区C。

一天，甲医疗队接到牧民区的求救电话，立刻设计了两种救助方案，方案 I ：从 A 地开车沿公路到离牧民区 C 最近的 D 处，再开车穿越草地沿DC方向到牧民区 C。

圆与三角函数1 •已知，如图，AB是。

O的直径，点C为。

O上一点，OF丄BC于点F,交。

O于点E, AE 与BC交于点H,点D为OE的延长线上一点，且/ ODBN AEC(1)求证：BD是O O的切线；(2)求证：CE二EH?EA(3)若。

O的半径为5，sinA^L，求BH的长.2•如图，已知AB是。

O的直径，C是。

O上任一点(不与A，B重合)，AB丄CD于E，BF为O O的切线，OF// AC,连结AF, FC, AF与CD交于点G,与。

O交于点H,连结CH.(1)求证：FC是O O的切线；(2)求证：GC=GE(3)若cos/ AOC=-, O O的半径为r,求CH的长.3•已知。

O是以AB为直径的厶ABC的外接圆，OD// BC交。

O于点D,交AC于点E,连接AD、BD, BD 交AC于点F.(1)求证：BD平分/ ABC;(2)延长AC到点P,使PF=PB求证：PB是。

O的切线；(3)如果AB=10, cos/ ABC」，求AD.54.如图，在矩形ABCD中，点O在对角线AC上，以OA的长为半径的圆O与AD、AC分别交于点E、F,且/ ACBd DCE(1 )判断直线CE与。

O的位置关系，并证明你的结论;(2)若上&门/ACB据,BC=2求O O的半径.5 •如图，AB是。

O的直径，D、E为。

O上位于AB异侧的两点，连接BD并延长至点C,使得CD=BD连接AC交。

O于点F,连接AE、DE、DF.(1 )证明：/ E=Z C;(2) 若/ E=55,求/ BDF的度数；(3) 设DE交AB于点G,若DF=4, cosB二，E是・，的中点，求EG?ED的值.E6. AB, CD是。

O的两条弦，直线AB, CD互相垂直，垂足为点E,连接AD,过点B作BF丄AD,垂足为点F,直线BF交直线CD于点G.(1) 如图1,当点E在。

O外时，连接BC,求证：BE平分/ GBC(2) 如图2,当点E在。

BCEBD 圆与三角函数例1.如图，Rt △ABC 中, ∠ACB=90°，AC=4， BC=2,以AB 上的一点0为圆心作⊙O 分别与AC ．BC 相切于点D ，E 。

(1)求⊙O 的半径。

(2)求sin ∠BOC 的值。

例2．如图，等腰△ABC 中，AB=A C ，以AB 为直径作⊙O ，交BC 于点D ，DE ⊥AC 于点E 。

(1)求证：DE 为⊙O 的切线(2)若BC=45，AE=1，求cos ∠AEO●专项训练：1．如图，已知Rt△ABC 和Rt△EBC，∠B=90°．以边AC 上的点D 为圆心， OA 为半径的⊙O 与EC 相切于点D ，AD∥BC. (l)求证： ∠E=∠ACB: (2)若AD=1, tan ∠DAC=22，求BC 的长．2．如图，已知点0是Rt △ABC 的直角边AC 上一动点，以D 为圆心，OA 为半径的⊙O 交AB 于D 点， DB 的垂直平分线交BC 于F,交BD 于E 。

(l)连结DF ，请你判断直线DF 与⊙O 的位置关系,并证明你的结论(2)当点D 运动到OA=2OC 时，恰好有点D 是AE 的中点，求tan ∠B 。

ADDA B3．如图，在△ABC中．AB=BC,以AB为直径的⊙O交AC于点D．过D作DF⊥BC,交AB的延长线于点E,垂足为F . (1)求证；直线DE是⊙O的切线；(2) 当∠E的值．4．如图，Rt△ABC中，∠C=90°，BD平分∠ABC，以AB上一点0为圆心，过B、D两点作⊙O，⊙O交AB于点E EF⊥AC于点F。

(1)求证：⊙O与AC相切：(2)若EF=2，BC =4，求tan∠A的值。

5．如图，△ABP中，∠ABP=90°，以AB为直径作⊙O交AP于点C，在弧AC上取一点F，使弧CF=弧CB，过C作AF的垂线，垂足为M，MC的延长线交BP于D。

(1)求证：CD为⊙O的切线。

(2)连BF交AP于B若BE=6，EF=2．求tan ∠FAE。

初三数学三角函数知识点归纳总结三角函数是数学中一个重要的概念，也是初三数学中的重点知识之一。

它们在几何、物理和工程学等领域有广泛的应用。

下面，我们将对初三数学中的三角函数知识点进行归纳总结。

1. 正弦函数正弦函数是三角函数中的一种，用sin表示。

在单位圆上，对于任意角度θ，点P(x, y)的坐标可以表示为P(θ, sinθ)，其中y坐标即为sinθ的值。

正弦函数的值域为[-1, 1]，定义域为所有实数。

2. 余弦函数余弦函数是三角函数中的另一种，用cos表示。

在单位圆上，对于任意角度θ，点P(x, y)的坐标可以表示为P(cosθ, θ)，其中x坐标即为cosθ的值。

余弦函数的值域也为[-1, 1]，定义域同样为所有实数。

3. 正切函数正切函数是三角函数中的一种，用tan表示。

正切函数可以表示为sinθ/cosθ，在θ=π/2+kπ（k为整数）的情况下，等于无穷大，即不存在定义。

正切函数的值域为所有实数，定义域除了θ=π/2+kπ之外的所有实数。

4. 反正弦函数反正弦函数是正弦函数的反函数，用arcsin表示。

在[-1, 1]的值域内，对于任意实数y，可以找到唯一的角度θ，使得sinθ=y，其中θ的范围在[-π/2, π/2]之间。

5. 反余弦函数反余弦函数是余弦函数的反函数，用arccos表示。

在[-1, 1]的值域内，对于任意实数x，可以找到唯一的角度θ，使得cosθ=x，其中θ的范围在[0, π]之间。

6. 反正切函数反正切函数是正切函数的反函数，用arctan表示。

在所有实数的定义域内，对于任意实数y，可以找到唯一的角度θ，使得tanθ=y，其中θ的范围在(-π/2, π/2)之间。

通过对上述知识点的了解，我们可以利用三角函数来解决一些有关角度和边长的问题。

在学习过程中，我们需要注意以下几个要点：1. 熟练掌握三角函数基本概念和符号表示，包括正弦函数、余弦函数和正切函数的定义、值域、定义域等。

三角函数与单位圆引言三角函数是数学中的重要概念，广泛应用于物理、工程、计算机图形学等领域。

而单位圆作为三角函数的基础，具有重要的几何和代数意义。

本文将探讨三角函数与单位圆之间的关系，以及它们在数学和实际应用中的重要性。

一、三角函数的定义三角函数包括正弦函数、余弦函数、正切函数等。

以正弦函数为例，它是一个周期函数，可以表示为f(x) = sin(x)，其中x为自变量。

正弦函数的定义域是实数集，值域是[-1, 1]。

通过图形可以看出，正弦函数的图像在一个周期内呈现出波浪形状，具有对称性。

二、单位圆的定义单位圆是一个半径为1的圆，圆心位于坐标原点(0, 0)。

单位圆的方程可以表示为x^2 + y^2 = 1。

单位圆上的点可以表示为(x, y)，其中x和y的取值范围是[-1, 1]。

单位圆在坐标平面上呈现出完美的对称性。

三、三角函数与单位圆的关系三角函数与单位圆之间存在密切的关系。

我们可以通过单位圆来解释三角函数的定义和性质。

1. 正弦函数与单位圆正弦函数可以通过单位圆上的点的y坐标来表示。

具体而言，对于一个角度x （弧度制），在单位圆上找到对应的点P(x, y)，那么y坐标即为sin(x)。

这是因为单位圆上的点到圆心的距离为1，而y坐标正好对应这个距离。

因此，单位圆上的点可以帮助我们直观地理解和计算正弦函数的值。

2. 余弦函数与单位圆余弦函数可以通过单位圆上的点的x坐标来表示。

具体而言，对于一个角度x （弧度制），在单位圆上找到对应的点P(x, y)，那么x坐标即为cos(x)。

这是因为单位圆上的点到圆心的距离为1，而x坐标正好对应这个距离。

因此，单位圆上的点可以帮助我们直观地理解和计算余弦函数的值。

3. 正切函数与单位圆正切函数可以通过单位圆上的点的y坐标和x坐标的比值来表示。

具体而言，对于一个角度x（弧度制），在单位圆上找到对应的点P(x, y)，那么y坐标除以x 坐标即为tan(x)。

这是因为正切函数定义为tan(x) = sin(x) / cos(x)，而单位圆上的点的坐标正好满足这个比值关系。

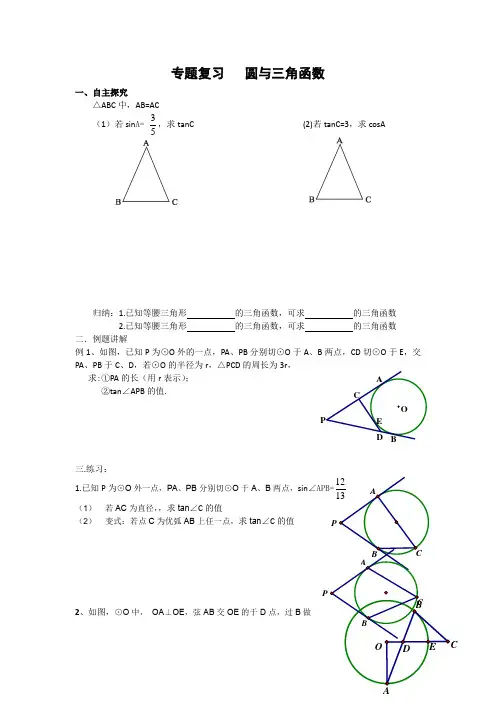
专题复习 圆与三角函数
一、自主探究
△ABC 中，AB=AC
（1）若sin A=
3
5
，求tanC (2)若tanC=3，求cosA
归纳：1.已知等腰三角形 的三角函数，可求 的三角函数 2.已知等腰三角形 的三角函数，可求 的三角函数 二．例题讲解
例1、如图，已知P 为⊙O 外的一点，PA 、PB 分别切⊙O 于A 、B 两点，CD 切⊙O 于E ，交PA 、PB 于C 、D ，若⊙O 的半径为r ，△PCD 的周长为3r ， 求:①PA 的长（用r 表示）；
②tan ∠APB 的值.
三.练习：
1.已知P 为⊙O 外一点，PA 、PB 分别切⊙O 于A 、B 两点，sin ∠（1） 若AC 为直径，，求tan ∠C 的值
（2） 变式：若点C 为优弧AB 上任一点，求tan ∠C 的值
2、如图，⊙O 中， OA ⊥OE ，弦AB 交OE 的于D 点，过B 做
P
34
⊙O 的切线，交OE 的延长线于C 点，若tan ∠A=
13
(1) 求证：CB=CD (2) 求sin ∠DCB 的值
3、如图，AB 是⊙O 的直径，CD 切⊙O 与点D ，CF ⊥AB 于E ，
若sin ∠C=45
（1） 求证：∠AOD=∠C （2） 求tan ∠A 的值
4.如图，在⊙O 中，弧AB=弧AC,D 为弧AB 上一点，若cos ∠BDC= ，求tan ∠ADC 的值。

F
O A
D。

第27讲三角函数与圆的综合知识导航1．明确同弧所对的弦、圆周角和圆的半经三者的关系：AB＝2RsinC，如图所示两种常用辅助线．C图1 图22．三角函数值形式上是两条线段的比值，往往可以转化为两个相似三角形的相似比．【板块一】求与圆有关的角的三角函数值方法技巧1．将所求角转化到直角三角形中；2．利用相似比进行转化。

题型一遇斜三角形作垂线构直角【例1】如图，AB是⊙O的直径，∠ABT＝45°，AT＝AB，连接OT交⊙O于点C，连接AC，求tan∠TAC的值．【解析】过点C作CD⊥TA于点D，设⊙O的半径为r，则AT＝AB＝2r，∴OT r，TC＝－1)r，∵CD∥OA，∴△TCD∽△TOA，∴CDOA＝TCTO＝TDTA，∴CD＝r，∴DA＝r，∴tan∠TAC＝CDDA＝．D【例2】如图，已知PA，PB分别与⊙O相切于点A，B，AC是⊙O的直径，连接BC，PC，若PB＝6，PC＝10，求sin ∠PCB的值．【解析】连OP，AB，则OP⊥AB，BC⊥AB，∴OP∥BC，∴∠PCB＝∠OPC，过点O作OM⊥PC于点M，∴sin∠PCA＝PAPC＝610＝35＝4OM，∴OM＝125，又OPsin∠PCB＝sin∠OPM＝．【点评】当所求锐角不在直角三角形中时，常作参线构造直角或利用等角特接求其三角函数值．题型二遇切线，连圆心切点构直角【例3】如图，BE，BC，CG分别与⊙O相切于E，F，G三点，且BE∥CG，延长BO交CG的延长线于点D，连接FG，若FGBD＝45，求sin∠CFG的值．【解析】易证OC⊥BD，OC⊥FG，∴FG∥BD，∴∠CFG＝∠CBD，连接OF，则OF⊥BC，可证△CFG∽△CBD，∴CF CB＝FGBD＝45，设CF＝4x，BC＝5x，∴BF＝x，易证OF2＝BF·FC＝4x2，∴OF＝2x，∴OB x，∴sin∠CFG＝sin∠OBF＝OFOB．【点评】注意等角转换与等比转换．题型三遇直径，利用直径构直角【例4】如图，在△ABC中，∠C＝90°，点D为BC的中点，以AC为直径的⊙O交AB于点E，若AEEB＝12，求cos∠BED的值．【解析】连接CE．由AEEB＝12，可设AE＝x，EB＝2x，易证上进△ACE∽△CBE，得CE2＝AE·BE＝2x2，∴CE，∴BC，由∠BEC＝90°，D是BC的中点可得DE＝BD，∴∠BED＝∠B，∴cos∠BED＝cos∠B＝BEBC＝．题型四遇弧的中点，利用垂径构直角【例5】如图，CD是△ABC的外角∠ECA的平分线，CD与过A，B，C三点的⊙O相交于点D．(1)求证：BD＝AD;(2)若AB＝CD，ABAC＝，求sin∠ACB的值。

初三圆周角函数知识点归纳总结圆周角函数是初中数学中的重要内容，对于学习三角函数和解题提供了便利。

本文将对初三圆周角函数的知识点进行归纳总结，以帮助同学们更好地理解和掌握。

一、正弦函数1. 定义：在单位圆上，从正半轴到与半径夹角为θ的弧段的纵坐标与半径的比值，称为正弦函数，记作sinθ。

2. 基本性质：- 定义域：所有实数；- 值域：[-1, 1]；- 周期性：sin(θ+2π)=sinθ；- 对称性：sin(-θ)=-sinθ。

3. 常用值：- sin(0)=0；- sin(π/6)=1/2；- sin(π/4)=√2/2；- sin(π/3)=√3/2；- sin(π/2)=1。

二、余弦函数1. 定义：在单位圆上，从正半轴到与半径夹角为θ的弧段的横坐标与半径的比值，称为余弦函数，记作cosθ。

2. 基本性质：- 定义域：所有实数；- 值域：[-1, 1]；- 周期性：cos(θ+2π)=cosθ；- 对称性：cos(-θ)=cosθ。

3. 常用值：- cos(0)=1；- cos(π/6)=√3/2；- cos(π/4)=√2/2；- cos(π/3)=1/2；- cos(π/2)=0。

三、正切函数1. 定义：在单位圆上，从正半轴到与半径夹角为θ的弧段的纵坐标与横坐标的比值，称为正切函数，记作tanθ。

2. 基本性质：- 定义域：所有实数，除去所有余弦函数为0的点（即θ=π/2+kπ，k为整数）；- 值域：全体实数；- 周期性：tan(θ+π)=tanθ。

3. 常用值：- tan(0)=0；- tan(π/4)=1；- tan(π/6)=√3/3；- tan(π/3)=√3；四、相关性质1. 三角函数的关系：- tanθ=sinθ/cosθ；- sin²θ+cos²θ=1。

2. 三角函数的互化公式：- sin(-θ)=-sinθ；- cos(-θ)=cosθ；- tan(-θ)=-tanθ。