下载文档原格式
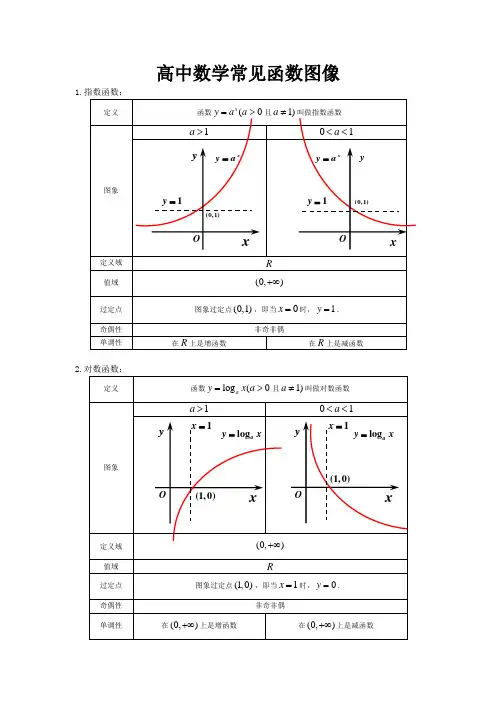
课件•指数函数基本概念与性质•指数函数运算规则与技巧•指数函数在生活中的应用举例•指数函数与对数函数关系探讨目录•指数方程和不等式求解技巧•总结回顾与拓展延伸01指数函数基本概念与性质指数函数定义及图像特点指数函数定义形如y=a^x（a>0且a≠1）的函数称为指数函数。
指数函数图像特点当a>1时，图像上升；当0<a<1时，图像下降。
图像均经过点(0,1)，且y轴为渐近线。
指数函数性质分析指数函数的值域为(0,+∞)。
当a>1时，指数函数在R上单调递增；当0<a<1时，指数函数在R上单调递减。
指数函数既不是奇函数也不是偶函数。
指数函数没有周期性。
值域单调性奇偶性周期性常见指数函数类型及其特点自然指数函数底数为e（约等于2.71828）的指数函数，记为y=e^x。
其图像上升速度最快，常用于描述自然增长或衰减现象。
幂指数函数形如y=x^n（n为实数）的函数，当n>0时图像上升，当n<0时图像下降。
特别地，当n=1时，幂指数函数退化为线性函数y=x。
对数指数函数底数为a（a>0且a≠1）的对数函数和指数函数的复合函数，记为y=log_a(a^x)=x。
其图像为一条直线，斜率为1，表示输入与输出之间呈线性关系。
复合指数函数由多个基本指数函数通过四则运算组合而成的复杂函数。
其性质取决于各基本函数的性质及组合方式。
02指数函数运算规则与技巧$a^m times a^n =a^{m+n}$，同底数幂相乘，底数不变，指数相加。
乘法法则除法法则幂的乘方法则$a^m div a^n =a^{m-n}$，同底数幂相除，底数不变，指数相减。
$(a^m)^n =a^{m times n}$，幂的乘方，底数不变，指数相乘。
030201同底数指数运算法则$a^m times b^m =(a times b)^m$，不同底数幂相乘，指数不变，底数相乘。
乘法法则$a^m div b^m =(a div b)^m$，不同底数幂相除，指数不变，底数相除。
高中数学常见函数图像1.2.对数函数：3.幂函数：定义形如αxy=（x∈R）的函数称为幂函数，其中x是自变量，α是常数.图像性质过定点：所有的幂函数在(0,)+∞都有定义，并且图象都通过点(1,1)．单调性：如果0α>，则幂函数的图象过原点，并且在[0,)+∞上为增函数．如果0α<，则幂函数的图象在(0,)+∞上为减函数，在第一象限内，图象无限接近x轴与y轴．4.函数sin y x =cos y x = tan y x =图象定义域R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时，max 1y =； 当22xk ππ=-()k ∈Z 时，min 1y =-．当()2x k k π=∈Z 时，max 1y =；当2x k ππ=+()k ∈Z 时，min 1y =-．既无最大值也无最小值周期性 2π2ππ奇偶性奇函数 偶函数 奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z 上是增函数；在32,222k k ππππ⎡⎤++⎢⎥⎣⎦ ()k ∈Z 上是减函数．在[]()2,2k k k πππ-∈Z 上是增函数；在[]2,2k k πππ+()k ∈Z 上是减函数．在,22k k ππππ⎛⎫-+⎪⎝⎭()k ∈Z 上是增函数．对称性对称中心()(),0k k π∈Z对称轴()2x k k ππ=+∈Z对称中心(),02k k ππ⎛⎫+∈Z⎪⎝⎭ 对称轴()x k k π=∈Z对称中心(),02k k π⎛⎫∈Z ⎪⎝⎭无对称轴。
