空间几何中的平行四面体的性质

高考常考内容1、正四面体和直四面体有哪些重要的性质？答：（1）正四面体的性质：设正四面体棱长为a，①全面积，体积；②对棱垂直，对棱间距距离；③相邻面所成二面角；④外接球半径；⑤内切球半径；⑥正四面体内任一点到各面距离之和为定值；⑦正四面体高为，外接球半径R与内切球半径r之比为.（2）直四面体的性质：直四面体O-ABC（OC、OB、OC两两垂直）.①外接球半径；②底面三角形ABC为锐角三角形；③（空间中的勾股定理，要注意平面与空间结论的类比）.◆典型例题◆题型1：空间几何体的构造1、（1）（06北京理4）平面的斜线 AB 交于点 B，过定点 A 的动直线与 AB 垂直，且交于点 C，则动点C的轨迹是（）A．一条直线B．一个圆C．一个椭圆D．双曲线的一支答案：A解析：设与¢是其中的两条任意的直线，则这两条直线确定一个平面，且斜线垂直这个平面，由过平面外一点有且只有一个平面与已知直线垂直可知过定点与垂直所有直线都在这个平面内，故动点C都在这个平面与平面的交线上，故选A。

（2）正方体ABCD_A1B1C1D1的棱长为2，点M是BC的中点，点P是平面ABCD内的一个动点，且满足PM=2，P到直线A1D1的距离为，则点P的轨迹是[]A.圆B.双曲线C.两个点D.直线答案：C解析：点P到A1D1的距离为，则点P到AD的距离为1，满足此条件的P 的轨迹是到直线AD的距离为1的两条平行直线，又，满足此条件的P的轨迹是以M为圆心，半径为2的圆，这两种轨迹只有两个交点.故点P的轨迹是两个点。

选项为C。

2、两相同的正四棱锥组成如图1所示的几何体，可放棱长为1的正方体内，使正四棱锥的底面ABCD与正方体的某一个平面平行，且各顶点均在正方体的面上，则这样的几何体体积的可能值有（）A．1个B．2个C．3个D．无穷多个答案：D解析：由于两个正四棱锥相同，所以所求几何体的中心在正四棱锥底面正方形ABCD中心，有对称性知正四棱锥的高为正方体棱长的一半，影响几何体体积的只能是正四棱锥底面正方形ABCD的面积，问题转化为边长为1的正方形的内接正方形有多少种，所以选D。

1四面体的性质不在一直线上的三点可以连成一个三角形，不共面的四点可以连成四个三角形，这四个三角形围成的几何体叫做四面体（如图1）.它有四个顶点，六条棱,四个面.研究四面体的有关性质可以加深对四面体,空间四边形的知识的理解，有利于提高熟练运用知识的能力。

性质1：四面体中相对的棱所在的直线是异面直线。

如图1中AB 和CD ，BC 和AD ，AC 和BD 都是异面直线。

性质2：四面体中，若一个顶点在对面内射影是这个三角形的垂心,则四面体的三组对棱分别互相垂直.证明：如图2的四面体中，设顶点A 在面BCD 内的射影H 是BCD △的垂心。

AH BCD ⊥平面。

连结BH ，CH ，DH,则BH CD ⊥，CH BD ⊥,DH BC ⊥.根据三垂线定理得AB CD ⊥，AC BD ⊥，AD BC ⊥.性质3：四面体中，若有两组对棱互相垂直,则第三组对棱也互相垂直。

证明：设四面体ABCD 中,AB CD ⊥，AC BD ⊥，过A作AH BCD ⊥平面，H 为垂足（如图2）.连结BH ，CH ，则BH 为AB 在平面BCD内的射影，根据三垂线定理的逆定理,BH CD ⊥；同理CH BD ⊥，所以H 是BCD △的垂心。

由性质2知AD BC ⊥.根据性质2，3立即可以得到：性质4：四面体中，若一个顶点在它对面内的射影是这个面的中心,则其余各顶点在其对面内的射影也分别是这些面的中心。

利用全等三角形的判定和性质,可以证明下面两条性质：性质5：四面体中，若交于同一顶点的三条棱相等，则这个顶点在对面内的射影是这个三角形的外心，且这三条棱和顶点所对面所成的角相等。

反之也真。

特别地，若这个顶点所对的面是一个直角三角形，则这顶点的射影是直角三角形斜边的中点。

性质6：四面体中，若一个顶点在对面内的射影是这个三角形的内心,则顶点到对面三角形三条边的距离相等，且以这三角形三角形三条边为棱的三个二面角相等.性质7:四面体中，若交于同一点的三条棱两两互相垂直，则这个顶点所对面是一个锐角三角形。

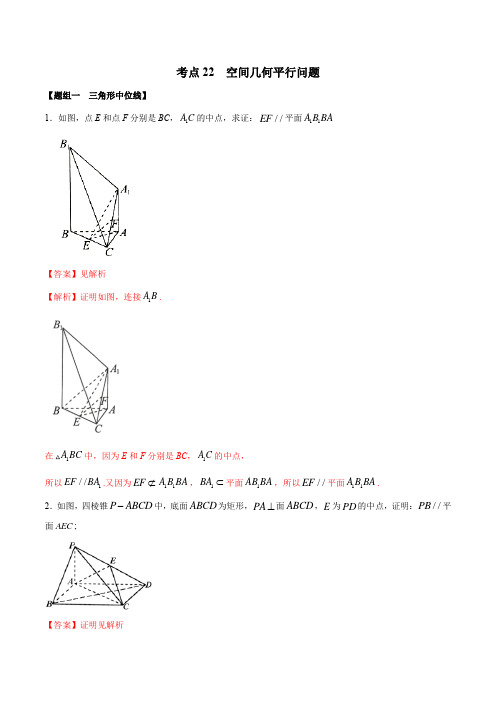
考点22 空间几何平行问题【题组一 三角形中位线】1．如图，点E 和点F 分别是BC ，1A C 的中点，求证：//EF 平面11A B BA【答案】见解析【解析】证明如图，连接1A B .在1A BC 中，因为E 和F 分别是BC ，1A C 的中点，所以1//EF BA .又因为EF ⊄11A B BA ，1BA ⊂平面1AB BA ，所以//EF 平面11A B BA .2．如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥面ABCD ，E 为PD 的中点，证明：//PB 平面AEC ;【答案】证明见解析【解析】设BD 交AC 于点O ，连结EO ．因为ABCD 为矩形，所以O 为BD 的中点．又E 为PD 的中点，所以EO ∥PB又EO 平面AEC ，PB 平面AEC 所以PB ∥平面AEC ．3．如图所示，在三棱锥P ABC -中，F 为BC 的中点，DE 垂直平分PC ，且DE 分别交AC PC ，于点,D E ，证明：//EF ABP 平面【答案】见解析【解析】证明：DE 垂直平分PC E ∴为PC 的中点 又F 为BC 的中点 EF ∴为BCP 的中位线 //EF BP ∴ 又,EF ABP BP ABP ⊄⊂平面平面 //EF ABP ∴平面4．如图,12AB AD CD ==,若M 为EA 中点,求证:AC ∥平面MDF【答案】证明见解析【解析】设EC 与DF 交于点N ,连结MN ,在矩形CDEF 中,点N 为EC 中点,如图:M 为EA 中点,∴MN ∥AC 又AC ⊄平面MDF ,MN ⊂平面MDF ∴AC ∥平面MDF ．5．已知四棱锥P ABCD -中，侧面PAD ABCD ⊥底面，PB AD ⊥，PAD △是边长为2的正三角形，底面ABCD 是菱形，点M 为PC 的中点，求证：PA MDB ∥平面【答案】证明见解析【解析】连结AC ，交BD 于O ，由于底面ABCD 为菱形，∴O 为AC 中点又M 为PC 的中点，//MO PA ，又MO MDB PA MDB ⊂⊄平面，平面//PA MDB ∴平面6．如图所示，在三棱柱ABC －A 1B 1C 1中，AC ＝BC ，点D 是AB 的中点，求证：BC 1∥平面CA 1D ．【答案】略【解析】证明：如图所示，连接AC 1交A 1C 于点O ，连接OD ，则O 是AC 1的中点．∵点D 是AB 的中点， ∴OD ∥BC 1.又∵OD ⊂平面CA 1D ，BC 1⊄平面CA 1D ，∴BC 1∥平面CA 1D.【题组二 构造平行四边形证线面平行】1．如图，四棱锥P ABCD -中侧面P AB 为等边三角形且垂直于底面ABCD ，12AB BC AD ==, E 是PD 的中点，证明：直线CE ∥平面PAB【答案】见解析【解析】取PA 的中点F ,连FE FB 、, E 是PD 的中点, ∴FE //=12AD , 又BC //=12AD ∴FE //=BC ∴四边形EFBC 是平行四边形 CE ∴∥BF 又CE ⊄平面PAB ,BF ⊂平面PAB CE ∥平面PAB2．如图，菱形ABCD ，,E F 分别是,AB PD 的中点，求证：//EF 平面PBC ；【答案】证明见解析【解析】解法一：（1）取PC 中点H ，连接FH ，BH .因为,E F 分别是,AB PD 的中点，所以////FH DC BE ，且12FH DC BE ==， 所以四边形EFHB 为平行四边形，所以//EF BH ，因为BH ⊂平面PBC ，EF ⊄平面PBC ，所以//EF 平面PBC .3．由四棱柱1111ABCD A B C D -截去三棱锥111C B CD -，后得到的几何体如图所示.四边形ABCD 为正方形，O 为AC 与BD 的交点，E 为AD 的中点，证明：1//AO 平面11B CD【答案】证明见解析【解析】如图②所示，取11B D 的中点1O ，连接111CO ,AO 由于多面体1111ABCD A B C D -是四棱柱，所以11//A O OC ，11A O OC =， 因此四边形11AOCO 为平行四边形，所以11//A O O C .又1O C ⊂平面11B CD ，1AO ⊄平面11B CD ，所以1//AO 平面11B CD . 4．在如图所示的五面体ABCDEF 中,四边形ABCD 为菱形,且60,22,//,DAB EA ED AB EF EF AB M ∠=︒====为BC 中点，求证:FM ∕∕平面BDE【答案】见解析【解析】取BD 中点O ,连接,OM OE ,因为,O M 分别为,BD BC 的中点,所以//OM CD ,且12OM CD =, 因为四边形ABCD 为菱形,所以//,CD AB CD ⊄又平面,ABFE AB ⊂平面ABFE ,所以//CD 平面ABFE .因为平面ABFE平面,CDEF EF CD =⊂平面CDEF ,所以CD EF ∕∕.又2AB CD ==,所以12EF CD =. 所以四边形OMFE 为平行四边形，所以//MF OE .又OE ⊂平面BDE ，且MF ⊄平面BDE ,所以//MF 平面BDE .【题组三 线面垂直证线面平行】1．如图所示，在正方体1111ABCD A B C D -中，M 是AB 上一点，N 是1A C 的中点，MN ⊥平面1A DC .求证：1//MN AD .【答案】证明见解析【解析】因为四边形11ADD A 为正方形，所以11AD A D ⊥.又CD ⊥平面11ADD A ，1AD ⊂平面11ADD A ，所以1CD AD ⊥.因为1A D CD D =，所以1AD ⊥平面1A DC .又MN ⊥平面1A DC ，所以1∥MN AD .2．已知正方体1111ABCD A B C D -，,E F 分别为AC 和1A D 上的点，且EF AC ⊥，1EF A D ⊥.（1）求证：1//EF BD ；（2）求证：1,,BE D F DA 三条直线交于一点.【答案】（1）详见解析；（2）详见解析【解析】证明：(1)如图，连结1AB 和1B C ，在正方体1111ABCD A B C D -中，11//A D B C ，∵1EF A D ⊥，∴1EF B C ⊥，又EF AC ⊥，1AC B C C ⋂=，∴1EF AB C ⊥平面．又在正方体1111ABCD A B C D -中，11B C BC ⊥，111B C D C ⊥,1111BC D C C ⋂=∴111B C BC D ⊥平面，又111BD BC D ⊂平面，∴11B C BD ⊥．同理可得11B A BD ⊥，又111B A B C B ⋂=，∴11BD AB C ⊥平面．∴EF ∥1BD .（2）由题意可得1EF BD <（或者1D F 和BE 不平行），又由(1)知EF ∥1BD ，所以直线1D F 和BE 必相交，不妨设1BE D F G ⋂=，则1G D F ∈，又111D F AA D D 平面⊂，所以11G AA D D ∈平面，同理G ABCD ∈平面．因为11AA D D ABCD AD ⋂=平面平面，所以G AD ∈，所以BE 、1D F 、DA 三条直线交于一点．【题组四 三角形相似比证线线平行】1．如图，在四面体A BCD -中，M 是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且3AQ QC =求证：//PQ 平面BCD .【答案】证明见解析【解析】如下图所示，取BD 的中点O ，在线段CD 上取点F ，使得3DF FC =，连接OP 、OF 、FQ .3AQ QC =，3AQ DF QC FC ∴==，//QF AD ∴，且14QF AD =.O 、P 分别为BD 、BM 的中点，//OP AD ∴，且12OP DM =. M 为AD 的中点，14OP AD ∴=. //OP QF ∴且OP QF =，四边形OPQF 是平行四边形，//PQ OF ∴.PQ ⊄平面BCD ，OF ⊂平面BCD ，//PQ ∴平面BCD .2．如图，三棱锥P ABC -中，PA ⊥底面ABC ，PA AB =，点E 、F 分别为P A 、AB 的中点，点D 在PC 上，且2PD DC =,明：//CF 平面BDE ；【答案】见解析【解析】设AE 中点为G ，连结GF ，GC ，则//GF EB ，//GF 平面EBD .32PG PC PE PD ==，∴//ED GC ，//GC 平面EBD ， ∴平面//GFC 平面EBD ，∴//FC 平面1EBD ；【题组五 线面平行性质证线线平行】1．如图，在三棱柱111ABC A B C -中，D 是BC 的中点，E 是11A C 上一点，但1//A B 平面1B DE ，则11A E EC 的值为_______. 【答案】12【解析】如下图所示，连接1BC 交1B D 于点F ，连接EF .在三棱柱111ABC A B C -中，11//BC B C ，11BDF C B F ∴∆∆， D 为BC 的中点，111122BD BC B C ∴==，11112BF BD FC B C ∴==. 1//A B 平面1B DE ，1A B ⊂平面11A BC ，平面11A BC ⋂平面1B DE EF =，1//A B EF ∴，11112A E BF EC FC ∴==，故答案为12. 2.如图，在多面体ABCDEF 中，DE ⊥平面ABCD ，AD ∥BC ，平面BCEF ⋂平面ADEF EF =，60BAD ︒∠=，2AB =，1DE EF ==,求证：BC ∥EF；【答案】证明见解析【解析】证明：∵AD ∥BC ，AD ⊂平面ADEF ，BC ⊄平面ADEF ，∴BC ∥平面ADEF .又BC ⊂平面BCEF ，平面BCEF 平面ADEF EF =，∴BC ∥EF ．3．如图所示，三棱柱111ABC A B C -中，点M ，N 分别是线段11A C ，1A B 的中点，设平面1MNB 与平面11BCC B 的交线为l ，求证：//MN l .【答案】证明见解析【解析】证明：如图所示，连接1C B ，在11A BC 中，点M ，N 分别为11A C ，1A B 的中点，所以1MN //C B . 又MN ⊄平面11BCC B ，1BC ⊂平面11BCC B ，所以//MN 平面11BCC B .又MN ⊂平面1MNB ，平面1MNB ⋂平面11BCC B l =，所以//MN l .4．如图所示，已知三棱锥A BCD -中，E ，F 分别是边AB ，AD 的中点，过EF 的平面截三棱锥得到的截面为EFHG ，求证：//EF GH .【答案】证明见解析【解析】证明：在ABD △中，因为E ，F 分别是边AB ，AD 的中点，所以由三角形的中位线定理可知//EF BD .又因为EF ⊄面BCD ，BD ⊂面BCD ，所以由线面平行的判定定理可知//EF 面BCD .又因为EF ⊂面EFHG ，面EFHG ⋂面BCD GH =，所以由线面平行的性质定理可知//EF GH .【题组六 面面平行性质证线线平行】1．在如图所示的五面体 ABCDEF 中，四边形ABCD 为平行四边形，//EF 平面ABCD ，2EA ED AB EF ===，M 为BC 的中点.求证：//FM 平面BDE .【答案】证明见解析【解析】取CD 的中点N ，连接MN 、FN .因为N 、M 分别为CD 、BC 的中点，所以//MN BD .又BD ⊂平面BDE ，且MN ⊄平面BDE ，所以//MN 平面BDE ，因为//EF 平面ABCD ，EF ⊂平面ABFE ，平面ABCD 平面ABFE AB =，所以//EF AB .又22AB CD DN EF ===，//AB CD ，所以//EF DN ，EF DN =，所以四边形EFND 为平行四边形，所以//FN ED .又ED ⊂平面BDE ，且FN ⊄平面BDE ，以//FN 平面BDE .又FN MN N ⋂=，所以平面//MNF 平面BDE .又FM ⊂平面MFN ，所以//FM 平面BDE .2．如图，在正四棱锥P ABCD -中，点F 在棱PA 上，且2PF FA =，点E 为棱PD 的中点,求证：CE //平面BDF【答案】见详解【解析】如图取PF 的中点M ，又2PF FA =，所以F 为MA 的中点，连接AC 交BD 于点O因为四边形ABCD 正方形，所以O 为AC 的中点又点E 为棱PD 的中点，所以ME //DF OF //MC ，又,OF FD F MC ME M ⋂=⋂=且,OF FD ⊂平面BDF ，,MC ME ⊂平面MCE所以平面BDF //平面MCE ，又CE ⊂平面MCE所以CE //平面BDF .3．如图，在四棱柱1111ABCD A B C D -中，底面ABCD 为梯形，//AD BC ，平面1A DCE 与1B B 交于点E .求证：1//EC A D .【答案】证明见解析【解析】因为BE ∥AA 1，AA 1⊂平面AA 1D ，BE ⊄平面AA 1D ，所以BE ∥平面AA 1D ．因为BC ∥AD ，AD ⊂平面AA 1D ，BC ⊄平面AA 1D ，所以BC ∥平面AA 1D ．又BE ∩BC ＝B ，BE ⊂平面BCE ，BC ⊂平面BCE ，所以平面BCE ∥平面AA 1D ．又平面A 1DCE ∩平面BCE ＝EC ，平面A 1DCE ∩平面AA 1D ＝A 1D ，所以EC ∥A 1D ．4．如图，已知四棱锥P ABCD -的底面为直角梯形，//AB CD ，90DAB ︒∠=，PA ⊥底面ABCD ，且112PA AD DC AB ====，M ，N 分别是PB ，PC 的中点.求证：//DN 平面AMC .【答案】证明见解析【解析】如图，连接DB 交AC 于点F . ∵12DC AB =，//DC AB ，∴12DF FB =. 取PM 的中点G ，连接DG ，FM ，则1122GM PM BM ==，GM DF BM BF ∴=， //DG FM ∴.又DG ⊄平面AMC ，FM ⊂平面AMC ，∴//DG 平面AMC .连接GN ，则//GN MC .又GN 平面AMC ，MC ⊂平面AMC ，∴//GN 平面AMC .又GN DG G ⋂=，∴平面//DNG 平面AMC .又DN ⊂平面DNG ，∴//DN 平面AMC .5．如图，在四棱柱''''ABCD A B C D -中，点M 和N 分别为1B C 和1D D 的中点、求证：//MN 平面ABCD .【答案】证明见解析.【解析】证明：如图， 设E 为棱1CC 的中点，连接NE ME ，.M N ，分别为1B C ，1DD 的中点，11////ME C B CB ∴，//NE CD .又ME NE ，在平面ABCD 的外部，//ME ∴平面ABCD ，NE ∥平面ABCD .又ME NE E ⋂=， ∴平面//MNE 平面ABCD .又MN ⊂平面MNE ，//MN ∴平面ABCD .【题组七 面面平行】1．如图，在正方体1111ABCD A B C D -中，,,M N P 分别是1AD ，1BD B C ，的中点. 求证：（1）MN ∥平面11CC D D ；（2）平面MNP 平面11CC D D .【答案】证明见解析【解析】（1）如图，连接1,AC CD .∵四边形ABCD 是正方形，N 是BD 的中点，∴N 是AC 的中点. 又∵M 是1AD 的中点，∴1//MN CD .∵MN ⊄平面11CC D D ，1CD ⊂平面11CC D D ，∴//MN 平面11CC D D .（2）连接1BC ，1C D ，∵四边形11B BCC 是正方形，P 是1B C 的中点，∴P 是1BC 的中点.又∵N 是BD 中点，∴1PN C D .∵PN ⊄平面111,CC D D C D ⊂平面11CC D D ，∴PN 平面11CC D D .由（1）知MN ∥平面11CC D D ，且MN PN N ⋂=， ∴平面//MNP 平面11CC D D .2．如图，在三棱柱111ABC A B C -中，E ，F ，G 分别为11B C ，11A B ，AB 的中点． ()1求证：平面11//A C G 平面BEF ；()2若平面11AC G BC H ⋂=，求证：H 为BC 的中点．【答案】（1）见解析（2）见解析【解析】 () 1如图， E ，F 分别为11B C ，11A B 的中点，11//EF A C ∴， 11A C ⊂平面11AC G ，EF ⊄平面11AC G ，//EF ∴平面11AC G ， 又F ，G 分别为11A B ，AB 的中点，1A F BG ∴=， 又1//A F BG ，∴四边形1A GBF 为平行四边形，则1//BF A G ， 1A G ⊂平面11AC G ，BF ⊄平面11AC G ，//BF ∴平面11AC G ， 又EF BF F ⋂=，∴平面11//A C G 平面BEF ； ()2平面//ABC 平面111A B C ，平面11A C G ⋂平面11111A B C A C =， 平面11AC G 与平面ABC 有公共点G ，则有经过G 的直线，设交BC H =， 则11//AC GH ，得//GH AC ， G 为AB 的中点，H ∴为BC 的中点．。

2023年高考数学考点复习——空间几何中的平行证明考点一、线线平行例1、如图，在四面体ABCD 中，E ，F 分别为DC ，AC 的中点，过EF 的平面与BD ，AB 分别交于点G ，H .求证：//EF GH证明：因为E ，F 分别为DC ，AC 的中点，所以//AD EF ，因为AD ⊄平面EFHG ，EF ⊂平面EFHG所以//AD 平面EFHG又平面EFHG ⋂平面ABD HG =，AD ⊂平面ABD所以//AD GH ，所以//EF GH .例2、如图，在四棱锥S -ABCD 中，底面ABCD 是菱形，60BAD ∠=︒，SAB ∆为等边三角形，G 是线段SB 上的一点，且SD //平面GAC .求证：G 为SB 的中点证明：证明：如图，连接BD 交AC 于点E ，则E 为BD 的中点，连接GE ，∵//SD 平面GAC ，平面SDB 平面=GAC GE ，SD ⊂平面SBD ，∵//SD GE ，而E 为BD 的中点，∵G 为SB 的中点.例3、在正四棱锥P ABCD -中，,E F 分别是,AB AD 的中点，过直线EF 的平面α分别与侧棱,PB PD 交于点,M N ，求证：//MN BD证明：证明：在ABD △中，因为E ，F 分别是,AB AD 的中点，所以EF BD ∕∕且12EF BD =， 又因为EF ⊄平面PBD ，BD ⊂平面PBD ，所以//EF 平面PBD因为EF ⊂平面,αα⋂平面PBD MN =，所以//EF MN ，所以//MN BD ．跟踪练习 1、如图，四边形ABCD 和三角形ADE 所在平面互相垂直，//AB CD ，AB BC ⊥，60DAB ∠=︒，4AB AD ==，AE DE ⊥，AE DE =，平面ABE 与平面CDE 交于EF ，求证：//CD EF证明：证明：因为//AB CD ，AB平面ABE ，CD ⊄平面ABE ，所以//CD 平面ABE ， 因为平面ABE 平面CDE EF =，CD ⊂平面CDE ，所以//CD EF .2、在四棱锥P ﹣ABCD 中，底面ABCD 为平行四边形E ，F 分别为BC ，AD 的中点，过EF 的平面与平面PCD 交于M ，N 两点，求证：//AB MN答案：证明见解析证明：∵底面ABCD 为平行四边形，E ，F 分别为BC ，AD 的中点，∵EF //CD ，∵EF //AB .EF ⊄平面PCD ，CD ⊂平面PCD ，所以//EF 平面PCD ，过EF 的平面与平面PCD 交于M ，N 两点，∵MN //EF ，∵AB //MN .3、如图，三棱锥P ABC -中，∵ABC 为正三角形，点1A 在棱PA 上，1B 、1C 分别是棱PB 、PC 的中点，直线11A B 与直线AB 交于点D ，直线11A C 与直线AC 交于点E ，求证：//DE BC证明：∵1B 、1C 分别是棱PB 、PC 的中点，∵11//B C BC ，∵11B C ⊄平面BCDE ，BC ⊂平面BCDE ，∵11//B C 平面BCDE ，∵11B C ⊂平面11B C DE ，平面BCDE ⋂平面11B C DE DE =，∵11//B C DE ，则//DE BC ；4、如图，四棱锥P ABCD -的底面是边长为8的正方形，点G.E.F .H 分别是棱PB ．AB ．DC ．PC 上共面的四点，//BC 平面GEFH.证明：//GH EF证明：∵//BC 平面GEFH ，又∵BC ⊂平面PBC 且平面PBC平面GEFH GH =，∵//BC GH .又∵//BC 平面GEFH ，又∵BC ⊂平面ABCD 且平面ABCD平面GEFH EF =，∵//BC EF ，∵//EF GH .5、如图，AE ⊥平面ABCD ，//BF 平面ADE ，//CF AE ，求证：//AD BC证明：依题意//CF AE ，CF ⊄平面ADE ，AE ⊂平面ADE ，∵//CF 平面ADE ，又//BF 平面ADE ，BF CF F ⋂=，∵平面//BCF 平面ADE ，∵平面BCF ⋂平面ABCD AD =，平面ADE平面ABCD BC =，∵//AD BC ；考点二、 线面平行例1、如图，正三棱柱ABC ﹣A 1B 1C 1中D 是AC 的中点，求证：B 1C ∵平面A 1BD证明：设AB 1与A 1B 相交于点P ，连接PD ，则P 为AB 1中点，∵D 为AC 中点，∵PD ∵B 1C ，又∵PD ∵平面A 1BD ，B 1C ⊄平面A 1BD ，∵B 1C ∵平面A 1BD例2、如图，在四棱锥A BCDE -中，底面BCDE 为矩形，M 为CD 中点，连接,BM CE 交于点,F G 为ABE △的重心，证明：//GF 平面ABC证明：延长EG 交AB 于N ，连接CN ，因为G 为ABE △的重心，则N 为AB 的中点，且2EG GN =， 因为//CM BE ，所以2EF BE FC CM ==，所以2EF EG FC GN==，因此//GF NC ， 又因为GF ⊄平面ABC ，NC ⊂平面ABC ，所以//GF 平面ABC ；例3、如图，四棱锥C ABED -中，四边形ABED 是正方形，若G ，F 分别是线段EC ，BD 的中点.（1）求证：//GF 平面ABC .证明：由四边形ABED 为正方形可知，连接AE 必与BD 相交于中点F ，又G 是线段EC 的中点，故//GF AC ，GF ⊄面ABC ，AC ⊂面ABC ，//GF ∴面ABC ；跟踪练习1、如图，在直三棱柱111ABC A B C -中，底面ABC 是等边三角形，D 是AC 的中点，证明：1//AB 平面1BC D证明：直三棱柱111ABC A B C -中，设1B C 与1BC 交于点E ，连接DE ，四边形11BCC B 是矩形，则E 为1B C 的中点，因D 是AC 的中点，所以1//DE AB ，又1AB ⊄平面1BC D ，DE ⊂平面1BC D ，所以1//AB 平面1BC D . 2、《九章算术》是我国古代的数学著作，是“算经十书”中最重要的一部，它对几何学的研究比西方要早1000多年.在《九章算术》中，将底面为直角三角形，且侧棱垂直于底面的三棱柱称为堑堵.如图，在堑堵111ABC A B C -中，，11AA AB AC ===，M ，N 分别是1CC ，BC 的中点，点P 在线段11A B 上，若P 为11A B 的中点，求证：//PN 平面11AAC C证明：证明：取11A C 的中点H ，连接PH ，HC .在堑堵111ABC A B C -中，四边形11BCC B 为平行四边形，所以11//B C BC 且11B C BC =.在111A B C △中，P ，H 分别为11A B ，11A C 的中点，所以11//PH B C 且1112PH B C =.因为N 为BC 的中点，所以12NC BC =， 从而NC PH =且//NC PH ， 所以四边形PHCN 为平行四边形，于是//PN CH .因为CH ⊂平面11AC CA ，PN ⊄平面11AC CA ，所以//PN 平面11AACC .3、如图，直四棱柱1111ABCD A B C D -的底面是菱形，12AA =，1AB =，E ，M ，N 分别是BC ，1BB ，1A D 的中点，证明：//MN 平面ABCD证明：连接1,ME B C ，,E M 分别为1,BC BB 中点，11//2ME B C ∴； 由直四棱柱特点知：11//A D B C ，11//2ME A D ∴，又N 为1A D 中点，//ME ND ∴， ∴四边形MNDE 为平行四边形，//MN DE ∴，又DE ⊂平面ABCD ，MN ⊄平面ABCD ，//MN ∴平面ABCD ；4、如图，在四棱锥P ABCD -中，四边形ABCD 是边长为2的菱形，M 是AB 的中点，N 是PD 的中点，PA AB =，求证：//MN 平面PBC证明：如图∵，取PC 的中点Q ，连接BQ ，NQ ，因为N 是PD 的中点，所以//NQ CD 且12NQ CD =.因为四边形ABCD 是菱形，M 是AB 的中点，所以//BM CD 且12BM CD =， 从而//BM NQ 且BM NQ =，所以四边形BMNQ 是平行四边形，从而//MN BQ .又MN ⊄平面PBC ，BQ ⊂平面PBC ，所以//MN 平面PBC . 5、如图，已知四边形ABCD 和BCEG 均为直角梯形，//AD BC ，//CE BG ，且2BCD BCE π∠=∠=，222BC CD CE AD BG =====，）求证：//AG 平面BDE答案：证明见解析证明：证明：过G 作GN CE ⊥于N ，交BE 于M ，连接DM ，如图所示：因为BC CE ⊥，且2CE BG =，所以N 为CE 中点，所以MG MN =，MNBC DA ，12MN AD BC ==， 所以MG AD ，MG AD =，所以四边形ADMG 为平行四边形，所以AG DM ，又DM ⊂平面BDE ，AG ⊄平面BDE ，所以AG 平面BDE .6、在四棱锥P —ABCD 中，AB //CD ，过CD 的平面分别交线段P A ，PB 于M ，N ，E 在线段DP 上(M ，N ，E 不同于端点)求证：CD //平面MNE证明：证明：∵//AB CD ，AB ⊂平面ABP ，CD ⊄平面ABP ∵//CD 平面ABP又∵CD ⊂平面CDMN ，平面CDMN 平面ABP MN =∵//CD MN又∵MN ⊂平面MNE ，CD ⊄平面MNE ∵//CD 平面MNE7、如图，在多面体ABCDEF 中，矩形BDEF 所在平面与正方形ABCD 所在平面垂直，1AB =，点M 为AE 的中点，求证：//BM 平面EFC证明：连接AC 交BD 于点N .连接MN .因为四边形ABCD 是正方形，所以N 为AC 的中点，由于M 为AE 的中点，所以//MN CE ， 又因为MN ⊄平面CEF ，CE ⊂平面CEF ，所以//MN 平面CEF ，易知//BN EF ，BN ⊄平面CEF ，EF ⊂平面CEF ，所以//BN 平面CEF ，因为MN BN N ⋂=，BN ⊂平面BMN ，MN ⊂平面BMN ，所以平面//BMN 平面CEF .又因为BM ⊂平面BMN ，所以//BM平面EFC ；8、在四棱锥P ABCD -中，底面ABCD 为梯形，//AB CD ，22AB CD ==，若Q 为AB 的中点，求证：//DQ 平面PBC证明：∵在梯形ABCD 中，//AB CD ，22AB CD ==，Q 为AB 的中点，所以//BQ CD 且BQ CD =，∵四边形BCDQ 为平行四边形，所以//DQ BC ，∵BC ⊂平面PBC ，DQ ⊄平面PBC ，所以//DQ 平面PBC ．9、如图所示，四面体P ABC 中，E ，F 分别为AB ，AC 的中点，过EF 作四面体的截面EFGH 交PC 于点G ，交PB 于点H ，证明：GH /平面ABC证明：∵E ，F 分别为AB ，AC 的中点,∵EF ∵BC ,又∵EF ∵平面PBC ,BC ∵平面PBC ,∵EF ∵平面PBC ,∵EF ∵平面EFGH ,平面EFGH ∩平面PBC =GH ,∵EF ∵GH ,又∵GH ∵平面ABC ,EF ∵平面ABC ,∵GH ∵平面ABC ;10、如图所示，在三棱柱111ABC A B C -中，D 为AC 的中点，求证：1//AB 平面1BC D证明：证明：如图，连接1B C 交1BC 于O ，连接OD ，∵四边形11BCC B 是平行四边形．∵点O 为1B C 的中点．∵D 为AC 的中点，∵OD 为1AB C 的中位线，∵1//OD AB ．∵OD ⊂平面1BC D ，1AB ⊄平面1BC D ，∵1//AB 平面1BC D ．11、如图，在四棱锥P ABCD -中，底面ABCD 是边长为2的正方形，PAB △为正三角形，且侧面PAB ⊥底面ABCD ，M 为PD 的中点，求证：//PB 平面ACM答案：证明见解析证明：证明：连接BD ，与AC 交于O ，在PBD △中，,O M 分别为,BD PD 的中点，//BP OM ∴,BP ⊄平面,ADE OM ⊂平面CAM ，//BP ∴平面CAM ；12、如图，在三棱柱111ABC A B C -中，侧面11ABB A 是菱形，E 是棱1BB 的中点，CA CB =，F 在线段AC 上，且2AF FC =，证明：1//CB 平面1A EF答案：证明见解析证明：连接1AB 交1A E 于点G ，连接FG ，因为四边形11ABB A 为菱形，则11//AA BB 且11AA BB =， E 为1BB 的中点，则11//B E AA 且1112B E AA =，故11112B G B E AG AA ==， 所以，1B G CF AG AF=，1//CB FG ∴， 1CB ⊄平面1A EF ，FG ⊂平面1A EF ，因此，1//CB 平面1A EF ；考点三、 面面平行例1、如图所示，四棱柱1111ABCD A B C D -的侧棱与底面垂直，12,,AC AA AD DC AC BD ====交于点E ，且,E F 分别为1,AC CC的中点，2BE =，求证：平面11//B CD 平面1A BD证明：如图，连接1AD ，设11AD A D H ⋂=，则H 为1AD 的中点，而E 为AC 的中点，连接EH ，则EH为1ACD △的中位线，所以1//EH CD ，又EH ⊄平面11B CD ，1CD ⊂平面11B CD ，所以//EH 平面11B CD ，又因为侧棱与底面垂直，所以1111//,=BB DD BB DD ，所以四边形11BB D D 为平行四边形，所以11//B D BD ，BD ⊄平面11B CD ，11B D ⊂平面11B CD ，所以//BD 平面11B CD ，又BD EH E ⋂=，,BD EH ⊂平面1A BD ，所以平面11//B CD 平面1A BD .例2、如图，在三棱锥P ABC -中，PAB △是正三角形，G 是PAB △的重心，D ，E ，H 分别是PA ，BC ，PC 的中点，点F 在BC 上，且3BF FC =，求证：平面//DFH 平面PGE证明：连结BG ，因为PAB △是正三角形，G 是PAB △的重心，D 为PA 的中点，所以BG 与GD 共线，且2BG GD =，因为E 为BC 的中点，3BF FC =，所以F 是CE 的中点， 所以2BG BE CD EF==，所以//GE DF ， 又GE平面PGE ，DF ⊄平面PGE ，所以//DF 平面PGE ， 因为H 是PC 的中点，所以FH //PE ，因为FH ⊄平面PGE ，PE ⊂平面PGE ，所以//FH 平面PGE ，因为FH DF F ⋂=，,FH DF ⊂平面DFH ，所以平面//DFH 平面PGE ；例3、如图，在多面体ABCDEF 中，ABCD 是正方形，2//AB DE BF BF DE ==，，，M 为棱AE 的中点，求证：平面//BMD 平面EFC证明：如图，连接AC ，交BD 于点N ，∵N 为AC 的中点，连接MN ，由M 为棱AE 的中点，则//MN EC ．∵MN ⊄面EFC ，EC ⊂面EFC ，∵//MN 平面EFC ．∵//BF DE BF DE =，，∵四边形BDEF 为平行四边形，∵//BD EF ．又BD ⊄平面EFC ，EF ⊂平面EFC ，∵//BD 平面EFC ，又MNBD N =， ∵平面//BMD 平面EFC ．跟踪练习1、如图，在几何体ABCDE 中，四边形ABCD 是矩形，2AB BE EC ===，G ，F ，M 分别是线段BE ，DC ，AB 的中点，求证：平面//GMF 平面ADE证明：如图，因为AB中点为M，连接MG，∥，又G是BE的中点，可知GM AE又AE⊆平面ADE，GM⊄平面ADE，所以GM平面ADE．在矩形ABCD中，由M，F分别是AB，CD的中点得MF AD．又AD⊆平面ADE，MF⊄平面ADE，所以MF平面ADE．⋂=，GM⊆平面GMF，MF⊆平面GMF，又因为GM MF M所以平面GMF平面ADE2、如图，四边形ABCD是边长为BB1＝DD1＝2，E，F分别是AD1，AB1的中点，证明：平面BDEF∵平面CB1D1证明：证明：连接AC ，交BD 于点O ，连接OE ，则O 为AC 的中点，∵E 是1AD 的中点，1//OE CD ∴OE ⊂平面BDEF ,1CD ⊄平面BDEF ,所以1//CD 平面BDEF又F 是1AB 的中点11//EF B D ∴EF ⊂平面BDEF ,11B D ⊄平面BDEF ,所以11//B D 平面BDEF又111,CD B D ⊂平面11CB D ,1111B D CD D ⋂=, 所以平面//BDEF 平面11CB D ．3、如图，已知矩形ABCD 所在的平面垂直于直角梯形ABPE 所在的平面，且EP =2BP =，1AD AE ==，AE EP ⊥，//AE BP ，F ，G 分别是BC ，BP 的中点，求证：平面//AFG 平面PEC证明：∵F ，G 分别是BC ，BP 的中点，∵FG CP ，且FG ⊄平面CPE ，则FG ∥平面CPE ，1BG PG AE ===，且//AE BP ，AE EP ⊥∵四边形AEPG 是矩形，则EP AG ∥，且AG ⊄平面CPE ，则AG平面CPE又GA GF G ⋂=，故平面//AFG 平面PEC4、如图，在四棱锥S -ABCD 中，底面ABCD 是直角梯形，AD //BC ，P ，Q 是AB ，CD 的中，点M ，N 分别是SB ，CB 的中点，求证∵平面AMN //平面SCD答案：证明见解析证明：因为M 、N 分别是SB ，CB 的中点，所以//MN SC ，MN ⊄面SCD ，SC ⊂面SCD ，所以//MN 面SCD ，又//AD CN 且AD CN =，所以ADCN 为平行四边形，所以//AN DC ，AN ⊄面SCD ，DC ⊂面SCD ，所以//AN 面SCD ，又AN MN N =，,AN MN ⊂面AMN ，所以面//AMN 面SCD ；5、如图，在三棱锥P ABC -中，PAB △是正三角形，G 是PAB △的重心，,,D E H 分别是,,PA BC PC 的中点，点F 在BC 上，且3BF FC =，求证：平面//DFH 平面PGE证明：证明：连结BG ，由题意可得BG 与GD 共线，且2BG GD =，∵E 是BC 的中点，3BF FC =，∵F 是CE 的中点，∵2BG BE GD EF==，∵//GE DF ，GE 平面PGE ；DF ⊄平面PGE ；∵//DF 平面PGE ， ∵H 是PC 的中点，∵//FH PE ，PE ⊂平面PGE ，FH ⊄平面PGE ；∵//FH 平面PGE ， ∵DF FH F =，DF ⊂平面DEF ，FH ⊂平面DEF ，∵平面//DFH 平面PGE ； 考点四 平行中的动点例1、直三棱柱111ABC A B C -所有棱长都为2，在AB 边上是否存在一点E ，使1//AC 平面1CEB ，若存在给出证明，若不存在，说明理由证明：存在，E 是AB 的中点，直三棱柱111ABC A B C -中，连接1BC 交1B C 于点O ，如图：则O 为1BC 中点，连接OE ，而E 为AB 的中点，则1//OE AC ，又1AC ⊄平面1CEB ，OE ⊂平面1CEB ，所以1//AC 平面1CEB ；例2、如图，在三棱柱111ABC A B C -中，1AA ⊥平面ABC ，90ACB ∠=︒，CA CB ==，1AA =D 是棱11A B 的中点，E 在棱1BB 上，且1AD EC ⊥，在棱BC 上是否存在点F ，满足//EF 平面1ADC ，若存在，求出BF 的值答案：存在，BF =证明：因为1AA ⊥面ABC ，故三棱柱111ABC A B C -为直三棱柱.故1AA ⊥面111A B C ，而1C D ⊂面111A B C ，故11AA C D ⊥，因为CA CB ==，故1111C A C B ==112B A =，因为D 是棱11A B 的中点，故111C D A B ⊥，因为1111AA A B A =， ∵直线1C D ⊥平面ADE ，而AD ⊂平面ADE ， ∵1C D AD ⊥，又1AD EC ⊥，111C D C E C ⋂=，∵AD ⊥平面1DEC ，而DE ⊂平面1DEC ，∵AD DE ⊥，在矩形11ABB A 中，11ADA DEB ∠=∠，11AA D DB E ∠=∠，故11ADA DEB ∠，故1111AA A D DB EB =11EB =即1=3EB ，故12BE EB =. 过E 作EG DE ⊥，交AB 于G ，取AB 的中点为L ，连接,DL CL ，则1DEB EGB ∠=∠，而190DB E EBG ∠=∠=︒，故1EBG DB E ， 所以11BG EB B E B D =31=，所以23BG =.在矩形11ABB A 中，因为11ADA DEB ∠=∠，故1ADA EGB ∠=∠，而1ADA DAL ∠=∠，所以EGB DAL ∠=∠，所以//AD EG ，而AD ⊂平面1ADC ，EG ⊄平面1ADC ，所以//EG 平面1ADC .在BC 上取点F ，使233BF BC ==，连GF ， 因为1BL =，故23BG BL =，故//GF CL . 在矩形11ABB A 中，因为,D L 为所在棱的中点，故11//,,DL AA DL AA =而1111//,,CC AA CC AA =故11//,CC DL CC DL =，故四边形1C DLC 为平行四边形，故1//DC CL ，故1//GF DC ，而1C D ⊂平面1ADC ，FG ⊄平面1ADC ，所以//FG 平面1ADC .因为GF EG G ⋂=，故平面以//EGF 平面1ADC ，因为EF ⊂平面EGF ，故//EF 平面1ADC .例3、如图，已知AD ⊥平面ABC ，EC ⊥平面ABC ，12AB AC AD BC ===，设P 是直线BE 上的点，当点P 在何位置时，直线//DP 平面ABC ？请说明理由证明：当点P 是BE 的中点时，//DP 平面ABC .理由如下：如下图，取BC 的中点O ，连接AO 、OP 、PD ，则//OP EC 且12OP EC =，因为AD ⊥平面ABC ，EC ⊥平面ABC ，所以//AD EC . 又12AD EC =，所以//OP AD 且OP AD =， 所以四边形AOPD 是平行四边形，所以//DP AO .因为AO ⊂平面ABC ，DP ⊄平面ABC ，所以//DP 平面ABC ；跟踪练习1、在三棱锥S ABC -中，AB ⊥平面SAC ，AS SC ⊥，1AB =，AC =，E 为AB 的中点，M 为CE 的中点，在线段SB 上是否存在一点N ，使//MN 平面SAC ？若存在，指出点N 的位置并给出证明，若不存在，说明理由证明：存在点N 为SB 上的靠近S 的四等分点即14SN SB =，//MN 平面SAC ， 证明如下：取AE 的中点F ，连接FN ，FM ，则//MF AC ，因为AC ⊂平面SAC ，MF ⊄平面SAC ，所以//MF 平面SAC ， 因为1124AF AE AB ==，14SN SB =， 所以FN //SA ，又SA ⊂平面SAC ，FN ⊄平面SAC ，所以//FN 平面SAC ，又MF FN F =，,MF FN ⊂平面MNF ，所以平面//MNF 平面SAC ，又MN ⊂平面MNF ，所以//MN 平面SAC ．2、在如图所示的五面体ABCDEF 中，∵ADF 是正三角形，四边形ABCD 为菱形，23ABC π∠=，EF //平面ABCD ，AB =2EF =2，点M 为BC 中点，在直线CD 上是否存在一点G ，使得平面EMG //平面BDF ，请说明理由证明：连接AC 交BD 于点O ，连接OM ，OF ，取CD 的中点G ，连接GM ，GE因为EF //平面ABCD ，EF ⊂平面ABEF ，平面ABEF ∩平面ABCD =AB ，所以EF //AB因为OM //AB //EF ，12OM AB EF ==，所以四边形OMEF 是平行四边形，所以OF //EM 因为EM ⊄平面BDF ，OF ⊂平面BDF ，所以EM //平面BDF因为点G 与点M 分别为CD 与BC 的中点，所以GM //BD因为GM ⊄平面BDF ，BD ⊂平面BDF ，所以GM //平面BDF而GM ∩EM =M ，平面EMG //平面BDF3、在长方体1111ABCD A B C D -中，已知AB AD =，E 为AD 的中点，）在线段11B C 上是否存在点F ，使得平面1//A AF 平面1ECC ？若存在，请加以证明，若不存在，请说明理由证明：存在，当点F 为线段11B C 的中点时，平面1//A AF 平面1ECC .证明：在长方体1111ABCD A B C D -中，11//AA CC ，11//AD B C .又因为1CC ⊂平面1ECC ，1AA ⊄平面1ECC ，所以1//AA 平面1ECC .又E 为AD 的中点，F 为11B C 的中点，所以1//AE FC ，且1AE FC =.故四边形1AEC F 为平行四边形，所以1//AF EC ，又因为1EC ⊂平面1ECC ，AF ⊄平面1ECC ，所以//AF 平面1ECC .又因为1AF AA A =，1AA ⊂平面1A AF ，AF ⊂平面1A AF ，所以平面1//A AF 平面1ECC .4、如图所示，在三棱柱ABC ﹣A 1B 1C 1中，平面ACC 1A 1∵平面ABC ，AA 1∵AC ，D ，D 1分别为AC ，A 1C 1的中点且AD =AA 1，在棱AA 1上找一点M ，使得1//D M 平面1DBC ，并说明理由答案：M 与A 重合时，1//D M 面1DBC ，理由见解析证明：当M 与A 重合时，D 1M ∵面DBC 1，理由如下：∵D 1C 1∵AD ，且D 1C 1=AD ，∵四边形D 1C 1DA 为平行四边形，∵D 1A ∵C 1D ，因为C 1D ∵面BDC 1，∵D 1M ∵面DBC 1.5、如图，在三棱锥P ABC -中，PA ⊥底面ABC ，ABC 是正三角形，E 是棱AB 的中点，如1AE =，在平面PAC 内寻找一点F 使得//BF 平面PEC ，并说明理由答案：答案见解析.证明：延长AC 至点G ，使得AC CG =，延长AP 至点H ，使得AP PH =，连接GH ，在直线GH 上任取一点F ，则点F 满足BF ∥平面PEC .理由如下： E 是线段AB 的中点，C 是线段AG 的中点，CE ∴是ABG 的中位线，∴BG CE ∥，BG ∴∥平面PEC .同理HG平面PEC ， 又BG HG G =，∴平面BHG平面PEC ， BF ⊂平面BHG ，BF ∴∥平面PEC .(注：若此题点F 直接取H 或G ，理由充分，给6分)6、已知四棱柱1111ABCD A B C D -的底面是边长为2的菱形，且BC BD =，1DD ⊥平面ABCD ，11AA =，BE CD ⊥于点E ，试问在线段11A B 上是否存在一点F ，使得//AF 平面1BEC ？若存在，求出点F 的位置；若不存在，请说明理由；证明：当F 为线段11A B 的中点时，//AF 平面1BEC .下面给出证明：取AB 的中点G ，连接EG ，1B G ，则1//FB AG ，且1FB AG =，所以四边形1AGB F 为平行四边形，所以1//AF B G .因为BC BD =，BE CD ⊥，所以E 为CD 的中点，又G 为AB 的中点，//AB CD ，AB CD =，所以//BG CE ，且BG CE =， 所以四边形BCEG 为平行四边形，所以//EG BC ，且EG BC =，又11//BC B C ，11BC B C =， 所以11//EG B C ，且11EG B C =，所以四边形11EGB C 为平行四边形， 所以11//B G C E ，所以1//AF C E ，又AF ⊄平面1BEC ，1C E ⊂平面1BEC ，所以//AF 平面1BEC ，7、在正三棱柱111ABC A B C -中，已知12,3AB AA ==，M ，N 分别为AB ，BC 的中点，P 为线段1CC 上一点．平面1ABC 与平面ANP 的交线为l ，是否存在点P 使得1//C M 平面ANP ？若存在，请指出点P 的位置并证明；若不存在，请说明理由证明：当2CP =时，1//C P 平面ANP证明如下：连接CM 交AN 于点G ，连接GP ，因为12CG CP GM PC ==，所以1//C M GP 又∵GP ⊂平面ANP ，1C M ⊄平面ANP ∵1C M 平面ANP。

空间几何中的平行四面体与正四面体知识点在空间几何学中，平行四面体和正四面体是两种常见的多面体。

它们具有不同的特点和性质，下面将详细介绍这两种多面体的知识点。

一、平行四面体平行四面体是指四个面中的任意两个面平行的四面体。

它具有以下几个重要的性质：1. 对角线平行性质：平行四面体的任意两条对角线都是平行的。

这是因为平行四面体的两个相对面平行，因此连接相对顶点的对角线也是平行的。

2. 面积比例性质：平行四面体的相邻两个面之间的面积比等于相邻两个对角面的面积比。

具体而言，如果平行四面体的两个相邻面的面积分别为S1和S2，而另外两个对角面的面积分别为S3和S4，则有S1/S2 = S3/S4。

3. 体积计算公式：平行四面体的体积可以通过以下公式计算：V = (1/3) * S * h，其中V表示体积，S表示底面积，h表示底面到顶点的距离。

4. 平行四面体的类型：根据底面形状的不同，平行四面体可以分为正方形底面四面体、长方形底面四面体和菱形底面四面体等多种类型。

二、正四面体正四面体是指四个等边等角的三角形构成的四面体。

它具有以下几个重要的性质：1. 边长和面积：正四面体的边长相等，每个面都是等边三角形。

正四面体的面积可以通过以下公式计算：S = (sqrt(3) * a2) / 4，其中S表示面积，a表示边长。

2. 高度和体积：正四面体的高度可以通过以下公式计算：h = (sqrt(6) * a) / 3，其中h表示高度，a表示边长。

正四面体的体积可以通过以下公式计算：V = (sqrt(2) * a3) / 12，其中V表示体积，a表示边长。

3. 正四面体的特殊点：正四面体有四个特殊的点，分别为顶点、底心、重心和垂心。

顶点是四个面的交点，底心是底面三角形三个高线的交点，重心是四个面重心连线的交点，垂心是底面三角形三条垂线的交点。

4. 对称性：正四面体具有四个三角对称面和六个对称轴。

四个三角对称面将正四面体分为等价的四个部分，而六个对称轴则是通过连接各个面的中点和顶点形成的。

空间几何中的平行四面体与棱锥平行四面体是一种特殊的多面体，它具有四个面，并且每个面都平行于与其相邻的面。

而棱锥是一种由一个多边形底面与一个点（顶点）连接而成的多面体。

在空间几何中，平行四面体和棱锥是两个重要的概念，在数学中有着广泛的应用。

一、平行四面体平行四面体是一个有四个面的多面体，它的四个面都是平行的。

平行四面体的边沿着四条平行线，而且四面体的对边相互平行且相等长。

四面体的对角线相交于一点，这个点被称为四面体的重心。

平行四面体的底面是一个平行四边形，而顶面则是底面平移得到的平行四边形。

平行四面体的体积可以通过底面积和高来计算。

如果底面的面积为S，高为h，则平行四面体的体积为V=1/3×S×h。

此外，平行四面体的表面积也可以通过底面积和侧面积来计算，其中侧面积为底面积的两倍。

二、棱锥棱锥是由一个多边形底面和一个顶点连接而成的多面体。

棱锥的侧面是由顶点和底面上的各个顶点连接而成的三角形。

顶点到底面的距离被称为棱锥的高，而底面的周长被称为棱锥的底面周长。

如同平行四面体一样，棱锥的体积可以通过底面积和高来计算，即V=1/3×底面积×高。

棱锥的种类较多，根据底面的形状可以分为三角棱锥、四边形棱锥、五边形棱锥等。

而根据棱锥的高与侧棱的关系，可以将其进一步分为直棱锥和斜棱锥。

直棱锥是棱锥的高与底面平行的，而斜棱锥则是两者不平行。

三、应用与性质平行四面体和棱锥在几何学中有着广泛的应用。

在计算几何中，平行四面体和棱锥的性质被用来推导和证明各种定理。

此外，在物理学和工程学中，平行四面体和棱锥被用来描述和求解各种物理和工程问题，比如计算体积和表面积，求解质心和重心位置等。

平行四面体和棱锥的性质也非常重要。

例如，平行四面体的中线是通过四面体的两个底面中心且平行于顶面的线段，它们相交于一个点。

而棱锥的高可以通过使用勾股定理和正弦定理计算得到。

这些性质的理解和应用对于解决各种几何问题至关重要。

第二十二章一般四面体的性质及应用【基础知识】四面体是三角形在空间的直接推广，三角形的很多性质及其证法可以推广到四面体上去．四面体的许多性质可以借助于平行六面体来证．性质1任意四面体六个内二面角的平分面交于一点，这点到四面体四个面的距离相等，该点称为四面体的内切球球心（简称四面体的内心）．内切球与四面体四个面内切． 若四面体ABCD 的体积为V ，顶点A 所对的侧面面积为A S ，类似地有B S ，C S ，D S （后面所设均同此），其内切球半径记为r ，则3A B C DVr S S S S =+++．性质2任意四面体六条棱的垂直平分面交于一点，这点到四面体四顶点的距离相等，该点称为四面体的外接球球心（简称四面体的外心）．外接球通过四面体四顶点． 若四面体ABCD 的体积为V ，其三对对棱的长分别为1a ，a ；1b ，b ；1c ，c ，其外接球半径为R ，则1624Q R V V===注其中Q 即为以三对对棱乘积为边的三角形面积． 性质3任意四面体的四条中线（每一顶点与其对面重心的连线）交于一点，而且每条中线从各该顶点算起都被这点分为31∶之比，这点称为四面体的重心． 性质4任意四面体的共顶点的（二面角的棱共顶点）三个内二面角的平分面与另三个内二面角的补（或外）二面角的平分面交于一点，这点到四面体四个面的距离相等，该点称为四面体的旁切球球心（简称四面体的旁心），且一个四面体有四个旁心，旁切球与四面体的一个侧面外切，与其他三个侧面的延展面相切．若与四面体ABCD 的顶点A 所对的面外切，与其余三个侧面的延展面相切的旁切球半径记为A r ，类似地有B r ，C r ，D r ，其他记号同前，则 3A B C D A V r S S S S =++-，3B A C D B Vr S S S S =++-，3C A B D C V r S S S S =+++，3D A B C DVr S S S S =+++．性质5（射影定理）四面体任意一个侧面的面积等于其他三个侧面在这个侧面上的射影面积之和．即在四面体ABCD 中，若记AB θ为棱AB 所在的内二面角的大小，其余类同，则有 cos cos cos A B CD C BD D BC S S S S θθθ=⋅+⋅+⋅， cos cos cos B C AD D AC A CD S S S S θθθ=⋅+⋅+⋅， cos cos cos C D AB A BD B AD S S S S θθθ=⋅+⋅+⋅， cos cos cos D A BC B AC C AB S S S S θθθ=⋅+⋅+⋅．性质6（余弦定理）四面体任意一个侧面的面积的平方，等于其他三个侧面的面积的平方和减去这三个侧面中每两个面面积及其所夹二面角余弦之积的两倍之和．即在四面体ABCD 中，有22222cos 2cos 2cos A B C D B C AD C D AB B D AC S S S S S S S S S S θθθ=++-⋅⋅-⋅⋅-⋅，22222cos 2cos 2cos B C D A C D AB C A BD D A BC S S S S S S S S S S θθθ=++-⋅⋅-⋅⋅-⋅，22222cos 2cos 2cos C A B D A B CD A D BC B D AC S S S S S S S S S S θθθ=++-⋅⋅-⋅⋅-⋅，22222cos 2cos 2cos D A B C A B AB A C BD B C AD S S S S S S S S S S θθθ=++-⋅⋅-⋅⋅-⋅．注顺次用A S ，B S ，C S ，D S 去乘射影定理中各式并相加整理即得以上第一式，其余各式类同． 性质7（体积公式一）四面体体积13=倍底面面积与底面上的高的乘积．即11113333A AB BC CD D v S h S h S h S h =⋅=⋅=⋅=⋅．性质8（体积公式二）四面体的体积等于它的任意两个面的面积及其所夹二面角正弦之积的三分之二，除以这两个面的公共棱长．即对四面体ABCD ，有2sin 2sin 2sin 2sin 3333C D AB A D BC A B CD B C DAS S S S S S S S V AB BC CD DAθθθθ⋅⋅⋅⋅⋅⋅⋅⋅====2sin 2sin 33B DAC A C BDS S S S AC BDθθ⋅⋅⋅⋅=． 注由2111sin sin 3332C C C AB C AB h AB V S h S h S AB θθ⋅⋅=⋅=⋅⋅=⋅⋅=⋅斜高斜高2sin 3C DABS S ABθ⋅⋅等即证得． 性质9（体积公式三）四面体的体积等于共顶点的三条棱长乘积与该顶点三面角的特征值乘积的六分之一，即对于四面体ABCD ，若共顶点A 的三条棱长分别为a ，b ，c ，顶点A 处的三个面角分别为α，β，γ则有()1166v abc S A =⋅=16abc =，()12ωαβγ=++． 其中()S A =A的三面角的特征值． 注由111sin sin 332V S h ab C γβ=⋅=⋅⋅⋅⋅性质10（体积公式四）若记1P ，2P ，3P分别为四面体相对两棱（互为异面的两条棱）的积的平方，再乘以另外四条棱的平方和与这对棱的平方和的差所得的积；P 为四面体每个面上三条棱的积的平方和，则四面体的体积V 性质11（正弦定理一）在四面体ABCD 中，有（1）sin sin sin sin C D AB A D BC B C DA B D ACAB BC DA ACS S S S S S S S θθθθ===⋅⋅⋅⋅⋅⋅⋅⋅2sin sin 3A B CD A C BD CD BD S S S S Vθθ===⋅⋅⋅⋅； （2）22sin sin sin sin sin sin 9A B C D AB CD AD BC AC BD S S S S AB CD AD BC AC BDVθθθθθθ⋅⋅⋅⋅⋅⋅===⋅⋅⋅；（3）若()sin A 表示顶点A 处的三棱中，任意两棱上的二面角的正弦与这两条棱夹角的正弦三者的积，余类同，则()()()()22sin sin sin sin 9C A B C D A B DS S S S S S S S A B C D V====．注此性质由性质8即证．性质12（正弦定理二）四面体中各个面上三条棱长的积与其所对三面角的特征值之比都相等，该比值等于六条棱长的积与体积的六倍之比，即对四面体ABCD ，有 ()()()()BC CD BD AC CD AD AB BD AD AB BC ACS A S B S C S D ⋅⋅⋅⋅⋅⋅⋅⋅===6AB BC CD BD AC ADV⋅⋅⋅⋅⋅=．注此性质由性质9即证，性质13（对棱所成角公式）四面体一对对棱所成角的余弦等于其他两对对棱平方和之差的绝对值与这对对棱乘积的二倍之比．即对四面体ABCD ，有 ¼()cos ,AB CD =()()22222BC AD AC BD AB CD+-+⋅；¼()cos ,BC AD =()()22222AB CD AC BD BC CD+-+⋅；¼()cos ,AC BD =()()22222BCAD AB DC AC BD+-+⋅；注其证明可参见第18章中例1或补成平行六面体，运用三角形余弦定理及平行四边形的对角线平方和等于四边平方和即证．性质14（对棱距离公式）若a 和1a ，b 和1b ，c 和1c 是四面体的三对对棱长，三对对棱之间的距离分别记为()1,d a a ，()1,d b b ，()1,d c c ，则 ()112,Vd a a =；()1,d b b =()1212,Vd c c =．注补成平行六面体证．性质15若四面体的一对对棱长分别为a ，1a ，这对对棱间的距离为d ，对棱所成的角为θ，则四面体的体积V 为11sin 6V aa d θ=⋅．性质16（二面角平分面定理）四面体二面角的内（或外）平分面分所对的棱得两条线段和这个二面角的两个面的面积对应成比例．性质17（空间张角公式）设过四面体ABCD 的棱BC 的截面EBC 交所对的棱AD 于E ，二面角A BC E --，E BC D --的大小分别为1θ，2θ，则 ()1212sin sin sin EBCDBC ABCS S S θθθθ+=+△△△． 性质18（空间莱布尼兹公式）设四面体ABCD 的六条棱长分别为a ，b ，c ，d ，e ，f ，G 为其重心，P 为空间中任一点，则()()2222222222211416PG PA PB PC PD a b c d e f =+++-+++++性质19（空间塞瓦定理）设E ，F ，G ，H ，M ，N 分别为四面体ABCD 的棱CD ，DB ，BC ，AD ，AB ，AC 上的点，若六个平面ABE ，ACF ，ADG ，BCH ，CDM ，DBN 共点，则 1CE DH AM BGED HA MB GC⋅⋅⋅= 性质20（空间梅涅劳斯定理）平面KLMN 交四面体ABCD 的棱AB ，BD ，CD ，AC 于K ，L ，M ，N ，则1AK BL DM CNKB LD MC NA⋅⋅⋅=．证明设四边形KLMN 是四面体ABCD 被平面α所截的截面，1AA ，1BB ，1CC ，1DD 是平面α的垂线（1A ，1B ，1C ，1D 分别为垂足）．考察棱AB 与平面α相交的部分，显然11AA K BB K △△≌，则11AA AK KB BB =．同理，11BB BL LD DD =,11DD BM MC CC =,11CC CN NA AA =． 以上四式两边相乘即证．性质21（空间斯特瓦尔特定理）在四面体ABCD 中．AD BC ⊥，过棱BC 作截面BCE 交棱AD 于E ，则222214BCE ABC BCD DE AE S S S BC AE DE AD AD =⋅+⋅-⋅⋅△△△．证明如图221-，作AF BC ⊥于F ，连BF ，DF ．注意到AD BC ⊥，知BC ⊥面ADF ，所以BC EF ⊥，BC EF ⊥．记AEF α∠=． 在AEF △中，由余弦定理，有 2222cos AF EF AE AE EF α=+-⋅⋅． 上式两边同乘以2BC 后，整理得EFBDC图22-1A222244cos 4BCE ABCBCES BC AE S AE BC S α+⋅-=⋅⋅△△△．同理在DEF △中，有222244cos 4BCE BCDBCES BE DE S DE BC S α+⋅--=⋅⋅△△△．由上述两式消去α，整理便证得结论．推论1当ABC BCD S S =△△时，有22214BCE ABCS S BC AE DE =-⋅⋅△△． 推论2当E 为AD 中点时，有222221112216BCE ABC BCD S S S BC AD =+-⋅△△△ 推论3当面BCE 平分二面角A BC D --时，有2214BCE ABC BCD S S S BC AE DE =⋅-⋅⋅△△△． 事实上，由ABC EABC BCD EBCD S V AE S V DE ==△△，有BCD ABC BCD S DE AD S S =+△△△，ABC ABC BCDS AECD S S =+△△△．由此即证． 推论4当AEk ED=时，有 ()222222111141BCE ABC BCD k k S S S AD BC k k k =+-⋅⋅⋅+++△△△． 性质22四面体ABCD 中，E ，F ，G ，H 分别在棱AB ，BC ，CD ，DA 上，且1AE EB λ=，2BFFCλ=， 3CG GD λ=，4DHHA λ=，则内接四面体EFGH 的体积与四面体ABCD 的体积之间有关系式 ()()()()1234123411111EFGH ABCDV V λλλλλλλλ⋅⋅⋅-=⋅++++．证明连ED ，BG ，得四棱锥E FBDG -，G EBDH -．在CBD △，ABD △中，有 ()()33232311111CFG CBD S CF CG S CB CD λλλλλλ⋅==⋅=⋅++++△△， ()()11141411111AEH ABD S AF AH S AB AD λλλλλλ⋅==⋅=⋅++++△△， ()()23223111FBDG CBD CFG CBD CBD S S S S S λλλλλ-++==++△△△△， ()()14414111ABD AFH EBDH ABD ABD S S S S S λλλλλ-++==++△△△△． 又()()()2321231111G FBDG FBDG ACBD CBD V S BE V S AB λλλλλλ-++=⋅=+++△ ()()()1441341111G EBDH EBDH CABD ABD V S GD V S CD λλλλλλ-++=⋅=+++△， ()()13111EBDG BDG ABDC BDC V S BE DG BE V S AB DC AB λλ=⋅=⋅=++△△． 设六面体EGFBDH 的体积为V '，则()()()()124224142324241231411111E FBDG G EBDH EBDG V V V V λλλλλλλλλλλλλλλλλλ--+++++++'=+-=++++ 设六面体FHEACG 的体积为V ''，则()()()()123134121334131231411111F GCAH H FCAE HACF V V V V λλλλλλλλλλλλλλλλλλ--+++++++'=+-=++++当B ，F 在平面EHG 的同侧时，有()EFGH ABCD V V V V '''=+-． 当C ，F 在平面EHG 的同侧时，有()EFGH ABCD V V V V '''==+． 综合，得()EFGH ABCD V V V V '''=-+．即证． 注由此性质可得E ，F ，G ，H 共面的充要条件是1AE BF CG DH EB FC GD HA⋅⋅⋅=． 【典型例题与基本方法】例1已知三棱锥S ABC -的底面是正三角形，A 点在侧面SBC 上的射影H 是SBC △的垂心，二面角H AB C --的平面角等于30︒，SA =S ABC -的体积．（1999年全国高中联赛题）解如图222-，由题设，知AH ⊥面SBC ，作BH SC ⊥于E ，则由三垂线定理知SC ⊥面ABE ．设S 在面ABC 的射影为O ，则SO ⊥面ABC ．由三垂线定理的逆定理，可知CO AB ⊥于F ．同理，BO AC ⊥．故O 为ABC △的中心，从而SA SB SC ===又CF AB ⊥，CF 是EF 在面ABC 上的射影，由三垂线定理知EF AB ⊥，所以EFC ∠是二面角H AB C --的平面角，故30EFC ∠=︒，cos6030OC SC =⋅︒=︒，tan603SO OC =⋅︒=．又OC AB =，则3AB ==，所以，21333S ABC V -=⋅例2证明：任意一个四面体总有一个顶点，由这个顶点出发的三条棱可以构成一个三角形的三边．（IMO 10-试题） 证明利用反证法来证，设四面体ABCD 中AB 是最长的棱，如果任意一个顶点出发的三条都不能构成一个三角形，则对由A 出发的三条棱，有AB AC AD +≥．又对由B 出发的三条棱，有BA BC BD +≥．两式相加，得2AB AC AD BC BD +++≥．()*但在ABC △与ABD △中，有AB AC BC <+，AB AD BD <+．此两式相加，有 2AB AC AD BC BD <+++． 上式与()*式矛盾，故原结论获证．注和这道试题类似的命题还有（1）任意四面体的三组对棱之和可以构成一个三角形的三边； （2）任意四面体的三组对棱之积可以构成一个三角形的三边；FOCBE HS图22-2A（波兰1975～1976年竞赛题）（3）任意四面体的三组对棱的平方和可以构成一个三角形的三边．例3若一个四面体恰有一棱之长大于1，求证这四面体的体积18V≤．证明如图223-，设AB是这个四面体的最长的棱，则ACD△，BCD△的边长不大于1．作BCD△的高BE和ACD△的高AF，则BE，AF1a≤表示CD的长度），四面体的高AO h AF=-≤111332BCDV h S a=⋅△≤()21424a a=-，而()()()()22431213a a a a a-=---+-≤，故当1a=时，()24a a-取最大值3，故31248V=≤．例4证明：在四面体中至多有一个顶点具有如下性质：该顶点处的任何两个平面角之和都大于180︒．（第22届莫斯科竞赛题）证明假定顶点A和B都具备所述的性质，则有180CAB DAB∠+∠>︒及180CBA DBA∠+∠>︒，但是作为CAB△和DAB△的全部6个内角之和也只有180180︒+︒，此为矛盾，从而原结论获证．例5设d是任意四面体的相对棱间距离的最小值，h是四面体的最小高的长．证明2d h>．（第24届全俄竞赛题）证明如图224-，为确定起见，假定h是四面体ABCD中由顶点A所引出的高，而d是棱AB和CD之间的距离．经过顶点B引直线l CD∥，过点A作平面垂直于棱CD交CD于F，交l于E，于是AEF△的高AH和FG就分别等于h和d．由于AEF△的第三条高等于四面体ABCD的某一条高，所以其值不小于h，因此AF EF≤，且图22-3B C图22-4HGlFE BDAC2h AH AE AF FE d FG FE FE+==<≤，此即为所证． 例6试证：过四面体相对棱的中点的任一截面平分四面体的体积．（IMO 29-预选题）证法1如图225-，设M 和P 分别是四面体ABCD 的棱AC 和BD 的中点，MNPQ 是四面体ABCD 的一个包含线段MP 的截面，因为P 为BD 的中点，则BCP CDP S S =△△，即有ABCP ACDP V V =．因此，要证截面MNPQ 将四面体ABCD 分成体积相等的两部分，只要证明AMNP V 与OMPQ V 相等就可以了．由N 和Q 分别作平面APC 的垂线，垂足分别为E ，F ，如图225-．因为M 为AC 的中点，则有APM CPM S S =△△，故要证AMNP CMPQ V V =，只要证NE FQ =即可．设MP 与NQ 交于点O ，易证E ，O ，F 三点共线．要证NE FQ =，只要证明NO OQ =就可以了（通过Rt Rt NEO QFO △△≌得到）． 为此，考察两个平行平面，异面直线AB 和CD 分别在这两个平面上（如图226-）．因为MP 是连接AC ，BD 中点的线段，所以它在与上述两平面平行的平面上，这个平面到两已知平面的距离相等．由于线段NQ 与MP 相交于O ，所以O 等分线段NQ ，即有NO OQ =．故结论获证． 注上述证明中，没有对截面MNPQ 的形状进行讨论．若对其形状进行讨论，则有下述两种证法． 证法2如图227-，设M ，P 分别是四面体ABCD 的对棱AC ，BD 的中点．OF E P QNMA BD图22-5N OP M QBDCA图22-6当截面是平行四边形或特殊三角形时，证明比较简单（略）． 当截面是一般四边形MNPQ 时． 由AM CM =，有A MNPQ C MNPQ V V --=又在ABC △中，对截线MNG 应用梅涅劳斯定理，有1AM CG BNMC GB NA⋅⋅=． 从而，有1CG BNGB NA⋅=． 同理，在BCD △中，有1BP DQ CG PD QC GB ⋅⋅=，即1DQ CGQC GB⋅=． 于是BN DQ NA QC =,得BN DQBA DC=． 又1C BPN Q APD V BN CDV BA QD--⋅==⋅,即C BPN Q APD V V --=． 故C MNPQ C BPN A MNPQ Q APD V V V V ---+=+一．证毕．证法3前面同证法2，下证截面为一般四边形MNPQ 时的情形．记A d 表示顶点A 到截面MNPQ 的距离（其余类同），设N 分AB 的比为m n ∶．则由M ，P 分别是AC ，BD 的中点，可知Q 点分CD 的比C A D B d d CQ AN mQD d d NB n====． 由A C d d =，有A MNPQ C MNPQ V V --=．又13113APD Q APDQ APD C BPNBPN C APD S d V AB QD m n n V NB CD n m n S d ----⋅+==⋅=⋅=+⋅△．即Q APD C BPN V V --=．故C MNPQ C BPN A MNPQ Q APD V V V V ----+=+．例7如图228-，设四面体1234A A A A 的外接球与内切球的半径分别为R 与r ，则3R r ≥．图22-7DG证明设O 为四面体的外心，i A 所对的面的面积为(14)i S i ≤≤，球心O 到i A 所对的面的距离为(14)i d i ≤≤，四面体体积为V ，过顶点1A 的高11A H h =，则易知1111d OA d R h +=+≥，从而()111113S d R S h V +⋅=≥，即1111133S d S R V ⋅+⋅≥．同理2221133S d S R V ⋅+⋅≥，3331133S d S R V ⋅+≥， 4441133S d S R V +⋅≥． 以上四式相加，并注意()1122334413S d S d S d S d V ⋅+⋅++⋅=， 有4113i i V R S V =+⋅∑≥4，即419i i R S V =⋅∑≥．因4113i i V r S ==⋅∑，从而44113i i i i R S r S ==⋅⋅∑∑≥，即3R r ≥．例8在四面体1234A A A A 中，顶点i A 所对的面的面积为(14)i S i ≤≤，侧面面积为k S ，j S 的两侧面所夹的内二面角的大小记为,k j()14k j <≤≤，棱k j A A 的中点记为kj M ，含点kj M 与另两顶点（不含顶点k A ，j A ）的三角形称为四面体的一个中线面（或一棱与对棱中点的面），这个中线面的面积记为kj S ()14k j <≤≤，则()22212cos ,4kj k j k j S S S S S k j =++⋅⋅，其中k ，j 满足14k j <≤≤．证明对四面体1234A A A A ，由性质6，有223434131423242cos cos 1,3cos 1,42,32,4S S S S S S S S S S S S +=⋅⋅++⋅+⋅⋅+⋅⋅+⋅⋅及221212131423242cos 1,2cos 1,3cos 1,4cos 2,3cos 2,4S S S S S S S S S S S S +=⋅⋅+⋅⋅+⋅⋅+⋅⋅+⋅⋅． 亦即13142324cos 1,3cos 1,4cos 2,3cos 2,4S S S S S S S S ⋅⋅++⋅+⋅⋅+⋅⋅2212122cos 1,2S S S S =+-⋅⋅．图22-843A 2A对四面体13412A A A M 和四面体23412A A A M 分别运用性质6，有2222123423411112cos 3,44422S S S S S S =++-⋅⋅⋅-3242112cos 2,32cos 2,422S S S S ⋅⋅-⋅⋅⋅，2222123413411112cos 3,44422S S S S S S =++-⋅⋅⋅-3141112cos 1,32cos 1,422S S S S ⋅⋅⋅-⋅⋅⋅上述两式相加，并将前面结果代入，有()22222123412131412cos 1,3cos 1,42S S S S S S S S S =+++-⋅⋅-⋅-232434cos 2,3cos 2,4cos 3,4S S S S S S ⋅⋅-⋅⋅-⋅⋅2212131411cos 1,3cos 1,422S S S S S S =+-⋅⋅-⋅-232411cos 2,3cos 2,422S S S S ⋅⋅-⋅⋅()222212121212cos 1,22S S S S S S =+-+-⋅ ()2212121cos 1,22S S S S =++⋅． 故()22212121212cos 1,24S S S S S =++⋅⋅． 同理，得()22212cos ,4kj k j k j S S S S s k j =++⋅⋅． 注由性质5，有421412cos ,k j t k j i S S k j S =⋅⋅=∑∑≤≤≤，则推知()22214141412cos ,4kj k j k j k j k j k j S S S S S k j <<⎡⎤=++⋅⋅⎢⎥⎣⎦∑∑∑≤≤≤≤≤≤≤ 444222111134i i i i i i S S S ===⎛⎫=+= ⎪⎝⎭∑∑∑ 例9设G 为四面体1234A A A A 的重心，则222222221232434213143444GA A A A A A A GA A A A A A A +++=+++ 222222223121424412132344GA A A A A A A GA A A A A A A =+++=+++21434k j k j A A =∑≤≤≤．43图22-9证明如图229-，连A ，G 并延长交面234A A A 于点1G ，则1G 是234A A A △的重心，连21A G 并延长交34A A 于M ，则M 是34A A 的中点．连1A M ，对12A A M △及点1G 应用斯特瓦尔特定理，有2221121211212211AG A M A A MG A M A G A M A G MG ⋅=⋅+⋅-⋅⋅．而21121A G G M =∶∶，则2222111212122339AG A A A M A M =+-．()* 由三角形中线公式，有 ()224211212341124A M A A A A A A =+-,()222222324341124A M A A A A A A =+-, 并将其代入()*，有()()2222222111213142324341139AG A A A A A A A A A A A A =++-++． 从而()()222222232221111213142324342324343314164GA A G A A A A A A A A A A A A A A A A A A ⎛⎫==+++++-++ ⎪⎝⎭．故22222123243414344k j k j GA A A A A A A A A <+++=∑≤≤．同理可证其他三式均等于例10设R ，r 分别为四面体1234A A A A 的外接球半径与内切球半径，i h 为顶点i A 到所对面的距离，内切球切各顶点i A 所对的面于i A '(1234)i =，，，．求证： （Ⅰ）21416k j k j A A R <∑≤≤≤；（Ⅱ）4214194k j i k j i A A h <=∑∑≤≤≤（Ⅲ）422164i i h r =∑≥；（Ⅳ）141419nk j k j i k j k j i A A A A X <<=''∑∑∑≤≤≤≤≤．证明（Ⅰ）设O ，G 分别为四面体1234A A A A 的外心和重心，延长1A G ，交面234A A A 于1G ，则1G 为234A A A △的重心，连21A G 交34A A 于M 点，则M 点为34A A 中点，如图229-． 由例9中证明，知2222222111213142324341[3()()]9AG A A A A A A A A A A A A =++-++． 同理，在四面体234OA A A 中，有222222212342324341[3()()]9OG OA OA OA A A A A A A =++-++．()222223243419R A A A A A A =-++ 由于G 为四面体重心，由性质3，知1131AG GG =．于是，在11AOG △中，对点G 应用斯特瓦尔特定理，有 ()222211111[433]16OG OG OA AG =+- 2222222121314232434116()()16R A A A A A A A A A A A A ⎡⎤=-++-++⎣⎦． 由于20OG ≥，故21416k j k j A A R <∑≤≤≤．（Ⅱ）显然11AG h ≥，则()()22222221121314232434139h A A A A A A A A A A A A ⎡⎤++-++⎣⎦≤． 同理，对2h ，3h ，3h 也有类似于上述的不等式．此四式相加，得4214194k j i k j i A A h <=∑∑≤≤≤．（Ⅲ）由13i i V S h =()1,2,3,4i =，则有4411113ii i iSh V ===∑∑又由4113i i V S r ==⋅∑，则4111i ih r ==∑．由14411234114i i h h h h h =⎛⎫ ⎪⎝⎭∑≥，有()412344h h h h r ≥． 故()()()114222222212341234448h h h h h h h h r r ⎡⎤+++=⎣⎦≥≥4．（Ⅳ）四面体1234A A A A ''''的外接球半径记为R '，则214116k j k j R A A <'''∑≤≤≥． 又四面体1234A A A A ''''的外接球半径恰是四面体1234A A A A 的内切球半径，故R r '=．于是4222214119999166416k j i k j i R A A h r R <='=∑∑≤≤≥≥≥≥14k j k j A A <''∑≤≤．故214149k j kj k j k j A A R A A <<'''∑∑≤≤≤≤≥8≥． 例11四面体1234A A A A 中，外接球半径为R ，体积为V ，过顶点k A ，j A 的中线面为()14kj S k j <≤≤．试证：141k j kjS <∑≤≤ 证明设1d ，2d ，3d 与1θ，2θ，3θ分别为三对对棱12A A ，34A A ；13A A ，24A A ；14A A ，23A A 的距离与夹角，则由性质15，有1234111sin 6V A A A A d θ=⋅⋅⋅，亦即113346V d A A A A ⋅≤． 同理，有213246V d A A A A ⋅≤，314236Vd A A A A ⋅≥．取34A A 的中点M ，则121212112MA A S S A A d =⋅△≥，同理，可得关于kj S 的不等式，从而412113214323324234111111112k j kj S A A d A A d A A d A A d A A d A A d <⎛⎫+++++ ⎪⋅⋅⋅⋅⋅⋅⎝⎭∑1≤≤≤122141413k j k j k j k j A A A A V <<⎫⎪⎭∑∑≤≤≤≤≤)12216R =例12设四面体1234A A A A 的内心为I ，记k j A IA △的面积为kj S '，顶点i A 所对的面的面积为i S ．试证：4141kji k j i S S <='∑≤≤ 证明过I 作1IA '⊥面234A A A 于1A '，作34IN A A ⊥于N ，若记面积为k S ，j S 的两侧面夹角为()14kj k j θ<≤≤，则易见11212A NI θ'∠=．设r 为四面体1234A A A A 的内切球半径，则在1Rt IA N '△中，有121sin 2rIN θ=,则34121212sin 2A A r S θ⋅'=． 由性质8，有1212342sin 3S S V A A θ⋅⋅=，于是消去34A A ，得12121221cos 32S V S S θ'⋅=⋅，注意到4113i i V S r ==⋅∑，则1212124121cos 2ii S S S S θ='''=⋅∑．对上述两边取∑，并用canchy 不等式，有1241414121cos 2kj k j k j ii S S θ<<=⎫'=⋅⎪⎭∑∑∑≤≤≤≤ 12241414121cos 2k j k j kj k j k j i i S S S S S θ<<=⎡⎤⎛⎫⎛⎫⋅⋅⋅⋅⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦∑∑∑≤≤≤≤≤．()* 注意到性质5，有1212313414cos cos cos S S S S θθθ=⋅+⋅+⋅，即42213121423411cos cos cos 2222i i S S S S θθθ==⋅+⋅+⋅∑， 对上式两边同乘以1S 后，再两边取∑，有241141cos 42kj i k j i k j S S S θ=<⎛⎫=⋅⋅ ⎪⎝⎭∑∑≤≤．又由对称平均不等式，有1421141146i k j i k j S S S =<⎛⎫=⋅ ⎪⎝⎭∑∑≤≤ 于是，由()*式（将上述结果代入()*式）即有414114kj i k j i S S <='∑≤≤．例13四面体1234A A A A 的三组对棱乘积的平方和不小于各侧面面积平方和的4倍，即若令12A A a =，34A A a '=，13A A b =，24A A b '=，14A A c =，23A A c '=，顶点i A 所对面的面积为()1234i S i =，，，，则 222222222212344()a a b b C C S S S S '''+++++≥，其中等号当且仅当各对棱的平方和相等．证明对234A A A △应用海伦一秦九韶公式，有 ()24442222221122216S a b c a b a c b c '''''''''=---+++ 同理，()24442222222122216S a b c a b a c b c '''=---+++， ()2444222223122216S a b c a b a c b c '''=---+++， ()24442222224122216S a b c a b a c b c '''=---+++． 以上四式相加并整理，得22221234S S S S +++=()()()()()()(){}2222222222222222222221416a a b b a a c c b b c c a a b b c c ⎡⎤⎡⎤⎡⎤'''''''''-+-+-+-+-+-++++⎣⎦⎣⎦⎣⎦()22222214a ab bc c '''++≤． 例14四面体1234A A A A 内一点P 到顶点i A 及i A 所对的面的距离分别为i l ，i d ，顶点i A 到所对的面的距离为()1234i h i =，，，，34k ≥ ．求证：41423ki k i i i l h d =⎛⎫ ⎪+⎝⎭∑≥．证明先证一个结论：设()01,2,3,4i x i >=，41i i x a ==∑，则4143ki k i i x a x =⎛⎫ ⎪-⎝⎭∑≥．其中等号当且仅当1234x x x x ===时取得．事实上，由()443333()44i i i i x a x a x a x ⎡⎤+-⎛⎫-=⎢⎥ ⎪⎝⎭⎣⎦≤，有443343k kk i i k i x x a x a ⎛⎫⎛⎫⎪ ⎪-⎝⎭⎝⎭≥，从而 4434444433314114443343k k k kk ii i i k ki i i x x x a x a a ===⎛⎫ ⎪⎛⎫⎛⎫ ⎪⋅=⎪ ⎪- ⎪⎝⎭⎝⎭⎪⎝⎭∑∑∑≥≥ 下证原题：设四面体1234A A A A 的体积为V ，如图2210-，作11A H ⊥面234A A A 于1H ，作11PE A H ⊥于E ，作1PD ⊥面234A A A 于1D ，则11A P l =，11PD d =，111A H h =．设i A 所对面的面积为(1234)i S i =，，，，则()1111111113S l S d S A E d S h V ⋅+⋅+==≥， 从而2341133PA A A S l V V ⋅-≥．同理，1342233PA A A S l V V ⋅-≥，1243333PA A A S l V V ⋅-≥， 1234433PA A A S l V V ⋅-≥．从而()13412412322334493PA A A PA A A PA A A V S l S l S l V V V +++-+≥()234111632PA A A V V S h d =+=+，即111112233442l S l h d S l S l S l '+++≥． 同理，222221133442l S l h d S l S l S l +++≥，333331122442l S l h d S l S l S l +++≥，444441122332l S l h d S l S l S l +++≥． 令()1,2,3,4i i i x l R i =⋅=，由前述结论，得4411423kki i ki i i i i l x h d a x ==⎛⎫⎛⎫ ⎪ ⎪+-⎝⎭⎝⎭∑∑≥≥． 【解题思维策略分析】1．解四面体的有关问题时，要善于与三角形类比A 3A 4图22-10例15一个球内切于四面体，将每个切点与该点所在面的三顶点连结起来，这样形成的每面的三个角（以切点为顶点）组成一个集合．试证这四个集合是相等的．（第16届普特南竞赛题）证明设四面体的顶点为()1234i P i =，，，，又设i Q 是正对着i P 的面与球相切的切点．用i ，j ，k ，l 表示{}1234，，，的不同元素，由于i j PQ 与i k PQ 是从同一顶点向球所作的切线，故ij i k PQ PQ =． 同理，i j i k PQ PQ =，从而i j l i k l PQ p PQ P △△≌（边，边，边）．于是i j l i k l PQ P PQ P ∠=∠， 并用il θ表示这种角，即有il li θθ=.由于以i Q 为顶点的三个角相加是2π，故有2334422πθθθ++=，3441132πθθθ++=，4112242πθθθ++=，1223312πθθθ++=．将这些等式的前两个相加减去后两个，且利用ij ji θθ=．得3412220θθ-=，即1234θθ=． 又由对称性，得ij kj θθ=．()*以1Q 为顶点的角是23θ，34θ，42θ，由()*式，它们分别等于以2Q 为顶点的三个角，即41θ，34θ，13θ． 由对称性，在所有四个面上的中心角都有同样的情形．证毕，注第26届IMO 由前苏联提供的预选题：“四面体ABCD 的内切球与面ABD 和DBC 分别相切于K 和M 点，证明：AKB DMC ∠=∠．”显然，这道试题是例15的特殊情形． 例16已知ABC △的面积力S △，外接圆半径为R ，过A ，B ，C 作平面ABC 的垂线，并在平面ABC 的同一侧的垂线分别取1A ，1B ，1C ，使1a AA h =，1b BB h =，1c CC h =，这里a h ，b h ，c h 分别表示边BC ，CA ，AB 边上的高．求四个平面11A B C ，11B C A ，11C A B ，ABC 所围成的四面体的体积．解求解此问题的关键是确定这个四面体的四个顶点的位置．设平面11A B C 与直线AB 相交于K 点，则点K 在11A B 上．由11AA BB ∥知11a b h AA KA b ACKB BB h a BC====．因此，K 是BCA ∠的外角平分线与BA 的交点，从而平面11A B C 与ABC 的交线是BCA ∠的外角平分线． 同理，类似可得：平面11B C A 与ABC 的交线是CAB ∠的外角平分线．上述两条外角平分线的交点是ABC △的旁心B I ，因此B I 就是平面11A B C ，11B C A 与ABC 的公共点，即为所求四面体的一个顶点．这样，旁心A I ，B I ，C I 是所求四面体的三个顶点．设第四个顶点为P ，则P 是平面11A B C 和11B C A 的公共点，因而在直线1B B I 上，P 在平面ABC 上的射影在B BI 上，也在A AI 上，因而P 的射影就是ABC △的内心I ．由相似三角形，1PI AA ∥，且1A P 与AI 相交于A I ，可得1a A a A ar rII PI PI AA h AI r -===，其中r 为ABC △的内切圆半径，a r 为劳切圆半径．设ABC △的周长为2l ，则11221a a a a r r S S l a l PE h r a l l a ---=⋅=⋅=-△．由平面几何知识，易证A B C I I I △的面积为 ()1222a b c S a b c S S ar br cr l a l b l c ⎛⎫'=+++=+++ ⎪---⎝⎭△△△()()()2abc S l a l b l c ⋅=---△． 故所求体积()()()211332A B C PI I I S abc S V S PI l l a l b l c ⋅'=⋅=⋅⋅---△△△1433abc S R ==⋅△． 例17在四面体1234A A A A 中，顶点i A 所对的面的面积记为()1234i S i =，，，，以i j A A 为棱的二面角为il θ，则 （Ⅰ）2142cos 3ij k j θ<∑≤≤≥；（Ⅱ）6141cos 3ij k j θ<≤≤≤C ． 证明联想到在ABC △中，运用三角形射影定理并结合柯西不等式，有2223cos cos cos 4A B C ++≥，31cos cos cos 2A B C ⋅⋅≤，于是有下述证法： （Ⅰ）由性质5，1234324423cos cos cos S S S S θθθ=⋅+⋅+⋅， 由Cauchy 不等式，有221234324423(cos cos cos )S S S S θθθ=⋅+⋅+⋅()()222222234342423cos cos cos S S S θθθ++++≤，从而22221342423222234cos cos cos S S S S θθθ++++≥． 同理，还有类似于上式的三个式子，四式相加，得2444222141112cos 4111i ii ij k j i i i i i i S x x S S x x θ<===⎛⎫==-++ ⎪---⎝⎭∑∑∑∑≤≤≥ ()1234141ix x x x x =-++++-∑()4411111641143133i i i ix x ==⎛⎫⎡⎤=-+-⋅-+= ⎪⎢⎥-⎣⎦⎝⎭∑∑≥． 故2142cos 3ijk j θ<∑≤≤≥． （Ⅱ）由1234324423cos cos cos S S S S θθθ=⋅+⋅+⋅≥．同理，还有类似于上式的三个不等式，此四式相乘，化简即得6141cos 3ij k j θ<∏≤≤≤． 注将三角形与四面体的上述两个不等式各统一为（Ⅰ）2111cos ,2k j n n i j n<++∑≤≤≥； （Ⅱ）()11211cos ,n n i j n i j n -+<+∏≤≤≤，其中2n =为三角形的，3n =为四面体的．2．善于将有关问题进行转化例18四面体ABCD 三个侧面ABD ，ACD ，BCD 上，由顶点D 引出的中线与底面ABC △对应边所成的角相等，证明：每个侧面的面积小于另外两个侧面面积之和．（1997年波兰竞赛题）证明设E ，F ，G 分别是边AB ，BC ，CA 的中点，连结DE ，DF ，DG 如图2211- （a ）．设DE 与AB 所成角为θ，则 1sin sin 2DAB S DE AB DE FG θθ=⋅⋅=⋅⋅△， 1sin sin 2DBC S DF BC DF GE θθ=⋅⋅=⋅⋅△， 1sin sin 2DCA S DG CA DG EF θθ=⋅⋅=⋅⋅△． 由于sin 0θ>，所要证明的命题转化为证明：在四面体DEFG 中，任意一组对棱的乘积小于另两组对棱乘积之和．为此，我们来证明： DE FG DF GE DG EF ⋅<⋅+⋅．将四面体DEFG 的面DFG △绕FG 翻转到底面所在的平面上，得D FG '△如图2211- （b ）．在四边形D FFG '中，显然，有D G DG '=，D F DF '=．由Ptolemy （托勒密）不等式，有D E GF D F GE D G EF DF GE DG EF '''⋅++⋅=⋅+⋅≤．设D E '与GF 交于点O ，由DFG D FG '△△≌，得DO D O '=．在DOE △中， DE DO OE D O OE D E ''<+=+=．故DE GF D E GF DF GE DG EF '⋅<⋅⋅+⋅≤．从而原题得证．例19给出三个四面体()123i i i i A B C D i =，，，过点i B ，i C ，i D 作平面i α，i β，i γ() 123i =，，分别与棱i i A B ，i i A C ，i i A D 垂直()123i =，，．如果九个平面i α，i β，i γ()123i =，，相交于一点E ，而三点1A ，2A ，3A 在同一直线l 上，求三个四面体的外接球面的交集（形状怎样？位置怎样？）．（CMO 3-试题）解由于几何元素太多，画出准确的全图几乎不可能．为此，画出一个局部图．COCDEFGABDEFG(b)(a)图22-11连1A E 与1B E 如图2212- （a ），可知111A B B E ⊥，此表明以1A E 为直径的球过1A ，1B ，E 三点．同样可知，这球过1A ，1B ，1C ，1D ，E 五点，此表明中心在1A E 的中点1O ，直径为1A E 的球也正好是四面体1111A B C D 的外接球．类似地可定出四面体i i i i A B C D 的外接球直径和中心()123i =，，． 于是问题转化为到直线123A A A 及其线外一点E 所决定的平面上来了．这个平面与三个球的交线是三个圆，它们有一个公共点E ，从E 向直线123A A A 作垂线，垂足为E '，显然E '是E 关于直线123O O O 的对称点，所以E 与E '是这三圆的公共点．由此知以EE '为直径且垂直于直线123A A A 的圆就是三个四面体的外接球的交集．当E 在直线123A A A 上时，此圆就退化为一个点E ．此时三个球面相切于E 点． 例20如图22-13，过四面体PABC 的重心G 的任一直线l 与四个面分别相交于M ，N ，S ，T 四点．求证：11110GM GN GS GT+++=u u u u r u u u r u u u r u u u r ．（《数学通报》问题1362题）证明设1G 为ABC △的重心，连1PG ，并设直线L 与直线1PG 确定的平面α与侧面ABC 的交线分别与ABC △的三边交于1A ，1B ，1C ．连1PA ，1PB ，1PC ，在平面α内，直线l 与1PA ，1PB ，1PC ，11A B 的交点分别为M ，N ，S ，T ．因G 是四面体重心，1G 是ABC △的重心，由重心性质，知G 分1PG u u u u r所成的比为31∶，且1112111110G A G B G C ++=u u u u r u u u u u r u u u u r ．231B 1图22-12(a)(b)B 1lG 1C 1A 1G TPNMSAC B图22-13以1G 为原点，以直线11G A 为x 轴，建立平面直角坐标系如图2214-．设()1,0A a ，()1,0B b ，()1,0C c ，(),P m n ，别由1112121110G A G B G C ++=u u u u r u u u u u r u u u u u r ，知1110a b c ++=，,44m n G ⎛⎫ ⎪⎝⎭．由两点式得直线1PA ，1PB ，1PC ，11A B 的方程分别为()n y x a m a =--，()ny x b m b=--， ()ny x c m c=--，0y = 设直线l 的参数方程为 1cos 41sin 4x m t y n t αα⎧=+⋅⎪⎪⎨⎪=+⋅⎪⎩（α为倾斜角，t 为参数） 并设M ，N ，S ，T 对应的参数分别为1t ，2t ，3t ，4t ． 将直线l 的方程分别代入直线1PA ，1PB ，1PC ，11A B 方程，得 114sin 4cos 4sin 33m n t na nααα-⋅-⋅=+， 214sin 4cos 4sin 33m n t nb nααα-⋅-⋅=+， 314sin 4cos 4sin 43m n t nc nααα-⋅-⋅=+，414sin t n α-= 由1110a b c++=，得123411110t t t t +++=，故11110GM GN GS GT +++=u u u ur u u u r u u u r u u u r ． 3．适当构作辅助体例21求证：若四面体相对棱间的距离分别为1d ，2d ，3d ，则四面体的体积V 不小于13123d d d ．图22-14证明如2215-，过四面体ABCD 的三组对棱AB 与CD ，AD 与BC ，AC 与BD ，分别引三对相互平行的平面，得平行六面体（或以四面体ABCD 的棱为侧面对角线构作平行六面体），各相对面的距离分别等于四面体三组对棱的距离，又易知该平行六面体的体积正好是四面体ABCD 体积的3倍． 在底面11A DB C 中，作1EF CA ⊥于E ，则1EF B D ⊥．设垂足为F ，则EF 不小于平面11A AC C 与平面11DD BB 间的距离，即3EF d ≥．又12AC d ≥，所以1123A DB CS d d ⋅≥Y ． 又平面11A DB C 与平面11AD BC 的距离为1d ，因此， 1111111123AD BC A DB C A DB C V S d d d d -=⋅⋅⋅≥Y ．Suoyi 12313ABCD V d d d ≥．例22设a ，b 为四面体ABCD 的一对对棱AB 与CD 的长，r 为四面体内切球半径，求证：()2abr a b <+．（第22届全苏竞赛题）证明如图2416-，过AB 与CD 分别作ABEF Y 与CDGH Y ，使得AF CD ∥，CH AB ∥，连AC ，BH ，EG ，FD ，得一个平行六面体AFEB CDGH -（或以四面体ABCD 的三棱CA ，CB ，CD 为共顶点的棱构成平行六面体）． 设AB 与CD 之间的距离为d ，它们所成的角为θ，则由性质15，知1sin 6V ab d θ=⋅⋅四面体．设a h 为ABD △中AB 边上的高，显然D 到AB 的距离大于D 到面AFEB 的距离，即a h d >，而1122ABD a S a h ad =⋅>△．同理，12ABC S ad >△，12ACD S bd >△，12BCD S bd >△．于是，四面体ABCD 的表面积D B CA EFC 1D 1A 1B 1图22-15GABCDHFE图22-16()ABD ABC ACD BCD S S S S S a b d =+++>+△△△△表．注意到性质1，即13V S r =⋅表，得到()3sin 222V abd abd ab r S S S a b θ⋅==<+表表表≤ 4．注意运用向量知识求解例23设平面α，β，γ，δ与四面体ABCD 的外接球面分别切于点A ，B ，C ，D ．证明：如果平面α与β的交线与直线CD 共面，则γ与δ的交线与直线AB 共面．（1981年保加利亚竞赛题）证明设四面体ABCD 的外心为O ，半径为R ．令OA a =u u u r ，OB =b u u u r ，OC c =u u u r ，CD d =u u u r．对空间中任意一点X ，令OX x =u u u r，则222222R =====a b c b d ．因为OA α⊥，所以平面α上的点X 满足()0⋅-=a x a ，即2⋅a x =R ． 同理，平面β，γ，δ上的点X 分别满足2R ⋅=b x ，2⋅c x =R ，2R ⋅=d x ． 注意到，对任意不同时为零的数λ，μ，有方程()()2R λλλμ⋅⋅+a b x =．给出了一个过平面α与β的交线l 的平面（因0λλ≠a +b ，且对任意X l ∈，有2R ⋅=⋅a x b x =．另外，对空间中任意一点X 也存在一对不同时为零的数λ，μ，使得()()220R R λμ⋅-+⋅-=a x b x ．即适当选取λ与μ，可使相应的平面过点X ．因此直线CD 与直线l 共面的充要条件是：关于未知数λ与μ的方程组()()()()22220,0,R R R R λμλμ⎧⋅-+⋅-=⎪⎨⋅-+⋅-=⎪⎩a c b c a c b c 有非零解，即有()()()()2222R R R R ⋅-⋅-=⋅-⋅-a c b c a b b c ． 同理可证，平面γ与δ的交线和直线AB 共面的充要条件为()()()()2222R R R R ⋅-⋅-=⋅-⋅-c a d b c b d a ．因为上面得到的两个条件是等价的，所以题中结论得证．例24设四面体ABCD 对应于各顶点的高分别为a h ，b h ，c h ，d h ，在各高线上分别取1A ，1B ，1C ，1D ，使1a k AA h =，1a k BB h =，1c k CC h =，1dkDD h =为任一实数．求证：四面体1111A B C D 的重心合于四面体ABCD 的重心． 证明令AB b =u u u r ，AC c =u u u r ，AD d =u u u r ，根据向量矢量积的意义，知同BD BC ⨯u u u r u u u r 的方向是对应A 点高线的方向，而它的长度是BCD △面积的2倍．设A 点对应高线的单位向量为i ，则2BCDBD BCi S ⨯=△u u u r u u u r，而()()BD BC ⨯=-⨯-=⨯⨯⨯d b c d b d +d c +c b u u u r u u u r ．故2i S⨯⨯⨯=b d +dc +c d．同理，设B ，C ，D 点对应的高线的单位向量分别为j ，k ，l ，则22ACD ACD AC AD S S ⨯⨯=△△c d j =u u u r u u u r ，2ADB S ⨯△d b k =，2ABCS ⨯△b c l =．若设四面体ABCD 的体积为V ， 因而()16a k k AA h V ==⨯⨯⨯i =b d +d c +c d u u u r ．同理，()16k BB V =⨯c d u u u r ，()16k CC V =⨯d b u u u u r ，()16kDD V =⨯b c u u u u r ． 因而，有11110AA BB CC DD +++=u u u r u u u r u u u u r u u u u u r． 又设1O 为四面体1111A B C D 的重心，则()1111111114AO A B AC A D =++u u u u r u u u u r u u u u r u u u u r()11111114A A AB BB A A AC CC A A AD DD =++++++++u u u r u u ur u u u r u u u r u u u r u u u u r u u u r u u u r u u u u r ()11111144A A AA BB CC DD =++++b +c +d +u u u r u u u r u u u r u u u u r u u u u r ()114A A =-b +c +d u u u r ． 而111AO AA A O =+u u u u r u u u r u u u u r ，故()114AO AO ==b +c +d u u u u r u u u r，这表示1O 与O 重合．【模拟实战】 习题A1．在三棱锥S ABC -的棱SA ，SB ，SC 上分别取点1A ，1B ，1C ，使得11SA SA SB SB ⋅=⋅1SC SC =⋅．证明：点A ，B ，C ，1A ，1B ，1C ．在同一球面上．（第15届全俄竞赛题）2．在四面体ABCD 内求作一点P ，使四个四面体的体积比满足P BCD P CDA P DAB P ABC V V V V αβγδ----=∶∶∶∶∶∶，其中α，β，γ，δ为给定的正数．3．设P ，Q ，R 分别是四面体ABCD 的棱AC ，AD ，AB 或延长线上的点，E ，F 在BC 上，且BE EF FC ==，AE ，AF 分别与RP 交于点G ，H ．记四面体APQR 与AGHQ 的体积分别为V ，1V ．求证：13V V ≥，当且仅当RP BC ∥或RP 与BC 重合时等号取得．4．四面体ABCD 内接于半径为R 的球，且球心O 在四面体内部．求证：四面体ABCD 至少有一条棱长． 5．在四面体ABCD 中，P 为各棱长之和，V 为其体积，用()CD S 表示过四面体棱CD 及相对棱AB 中点。

空间几何中的平行四面体在空间几何学中，平行四面体是一个非常重要的概念。

它是由四个平行的且不在同一平面的三角形构成的多面体。

本文将介绍平行四面体的定义及性质，并给出一些相关的例子和应用。

一、平行四面体的定义平行四面体是由四个平行的且不在同一平面的三角形所组成的多面体。

它具有以下特点：1. 四个面都是三角形。

2. 相邻两个面之间的边都是平行的。

3. 任意两个不相邻的面之间的距离是相等的。

二、平行四面体的性质1. 平行四面体的对棱平行且相等。

对任意的棱AB和CD，若AB ∥ CD，则有AB=CD。

2. 平行四面体的对顶角平等。

对任意的顶点O和底面P，若∠AOC=∠BOD，则有∠DOP=∠COP。

3. 平行四面体的任意两个面之间的距离相等。

对于任意的两个面ACDF和BCEF，有AC=BD。

4. 平行四面体的四条棱构成的四面体是平行四面体，且与原平行四面体全等。

5. 平行四面体的底面积乘以高等于体积。

设底面为底的面积为S，其高为H，则平行四面体的体积V=SH/3。

三、平行四面体的例子1. 双峰山：双峰山位于中国的广东省韶关市。

它的山势独特，由四个平行的山脊组成，形成了一个平行四面体的形状。

2. 锡尔河四面体：位于俄罗斯的锡尔河口以北，是一个由四条平行的山脉组成的地貌景观。

3. 钻石：钻石的晶体结构可以看作是一个平行四面体的形状，钻石的每个面都是一个等边三角形。

四、平行四面体的应用1. 三维建模：在计算机图形学和三维建模领域，平行四面体常被用于表示物体的三维空间结构。

2. 计算几何：平行四面体是计算几何中的重要概念，可以用来求解空间中的各种几何问题。

3. 数学教学：在数学教学中，通过平行四面体的例子可以引导学生理解三维空间的概念，并进行相关的几何推理。

总结：平行四面体是空间几何学中的一个重要概念，它由四个平行的且不在同一平面的三角形组成。

它具有一系列独特的性质，如对棱平行且相等、对顶角平等等。

平行四面体在实际生活中也有很多应用，如三维建模、计算几何等。

空间几何的性质四面体的性质及其应用四面体是空间中常见的立体图形，它具有一些独特的性质和应用。

本文将介绍四面体的性质及其应用。

一、四面体的定义和性质四面体是由四个三角形面组成的立体图形。

它具有以下性质：1. 定义：四面体是由四个不在同一平面上的点及连接这些点的边组成的立体。

2. 面积和体积：四面体的表面积和体积可以通过一定的公式计算得出。

其中，表面积等于四个三角形面积之和，体积等于底面积乘以高的一半。

3. 棱和顶点：四面体有六条棱和四个顶点。

任意两个顶点之间可以连接一条棱。

4. 高、中线和外接球：四面体的高是从一个顶点到相对的底面的垂直距离。

每个面的中线是连接该面上的两个中点的线段。

四面体还可以围绕外接球，外接球的球心与四面体的顶点都在同一平面上。

二、四面体的分类根据四面体的性质，我们可以将其分为以下几类：1. 正四面体：如果四面体的四个面都是等边三角形，那么它就是正四面体。

正四面体具有对称性，在空间几何学中起到重要作用。

2. 正交四面体：如果四面体的三个互相垂直的棱对同时相等，那么它就是正交四面体。

正交四面体具有一些特殊的性质，常用于计算几何和物理学中。

3. 锐角四面体和钝角四面体：根据四个顶点形成的凸四面体的内角是锐角还是钝角，可以将四面体分为两类。

在实际应用中，这些分类有助于确定四面体的稳定性和结构特征。

三、四面体的应用四面体不仅具有美学价值，还在许多领域有实际应用：1. 建筑与工程学：在建筑设计和工程施工中，四面体的结构特性可以用于设计和计算支撑结构的强度和稳定性。

2. 化学与结晶学：在化学和结晶学研究中，四面体被广泛用于分子和晶体的描述和分析。

3. 三维造型与动画：计算机图形学中，四面体被用于表示和生成三维模型和动画效果。

4. 数学与几何学：四面体是数学和几何学中研究的重要对象之一，对于解决空间几何问题和推导数学定理有重要意义。

总结：四面体是空间几何中重要的立体图形，具有独特的性质和应用。

四面体的特殊性原理四面体是一个具有四个面的多面体，每个面都是一个三角形。

它是空间中最简单的多面体之一，具有许多特殊性质和原理。

1.形状特性：四面体的最基本特性是其形状。

正四面体是最常见的四面体类型，其四个面都是等边三角形，并且所有的内角也相等。

正四面体具有对称性，每个面都等效地相对于其他三个面。

这种形状特性使得正四面体具有优秀的稳定性和抗力特性。

2.内外共点性：四面体的一个重要特性是其四个顶点共面且共点。

换句话说，四面体的顶点均位于同一平面上，这被称为“共点性”。

这个特性很容易证明，只需考虑四面体的两个对角线，它们必定会相交于一个点。

3.顶点对称性：四面体的另一个重要特性是其顶点的对称性。

四面体的顶点分别对称于其他三个顶点，具有相同的距离和角度关系。

这种对称性使四面体在空间中具有优雅和美学上的特殊性。

4.重心性质：四面体的重心是四个顶点的平均值，即四个顶点的坐标均值。

重心在许多应用中起着重要的作用，例如在计算力学性质时，求解质心是简化计算和分析的关键步骤。

每个面的重心位于该面的中心，而整个四面体的重心位于整个四面体内部的一个点上。

5.体积与高度的关系：四面体的体积可以根据其底面积和高度计算得出。

四面体的高度是从底面到对面顶点上垂线的距离。

根据勾股定理，四面体的高度可以通过底边长和平行于对面底边的高边的长度计算得出。

四面体的体积是其底面积和高度的乘积的1/3倍。

6.四面体剖分：四面体可以通过不同的剖分方式展示其特殊性质。

例如，当将四面体通过从顶点到对面底边作垂线分成两个小的四面体时，这两个小的四面体与原始四面体具有相似性质。

该剖分方式可以应用于几何中的许多问题，例如计算体积和表面积。

7.点与平面的关系：一个点可以描述为一个四面体的顶点，而四面体的三个面可以描述为三个相交的平面。

这种关系在几何学和图形学中得到广泛应用，例如在计算射线与平面的交点时。

8.斜四面体的稳定性：斜四面体是指四个面都是三角形，但不满足等边性质的四面体。