【最高考】高考数学二轮专题突破高效精练 第14讲 空间几何体的表面积与体积

高考二轮专题复习【空间几何体】空间几
何体的表面积与体积
本题考查了由三视图求几何体的表面积，根据三视图判断几何体的形状及数据所对应的几何量是解题的关键．本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及数据所对应的几何量是解题的关键．规律总结：柱、锥、台、球体及其简单的组合体的表面积与体积问题是历年高考必考内容，把简单几何体的表面积、体积问题与三视图结合在一起是近几年的热点问题，而多面体与球的组合问题(特别是球的外接与内切问题)既是近几年的热点问题，又是难点问题．简单几何体的表面积与体积的考查，一般为中低档试题，但近年有加大难度的趋势；且创新力度较大，一般以选择题、填空题为主．。

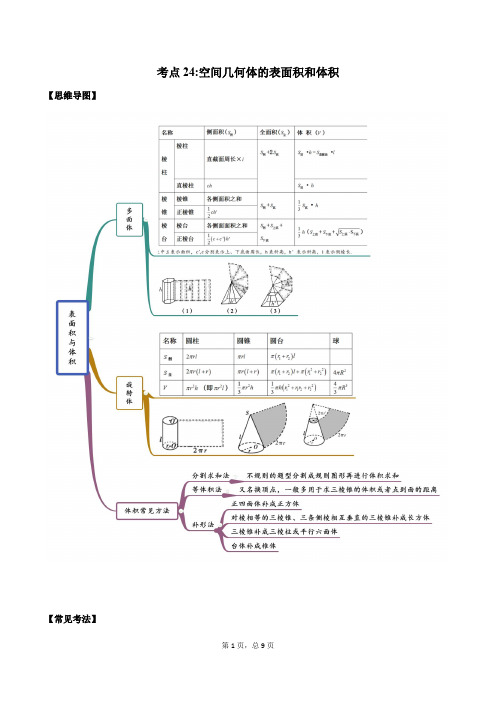
考点24:空间几何体的表面积和体积【思维导图】【常见考法】考法一：体积1．（等体积法之换顶点）如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，22AD BD AB ===，平面PAD ⊥底面ABCD ，且PA PD ==E ，F 分别为PC ，BD 的中点.（1）求证：//EF 平面PAD ；（2）求证：平面PAD ⊥平面PBD ；（3）求三棱锥B PCD -的体积.2.（等体积法之点面距）已知三棱锥A BPC -中，,AP PC AC BC ⊥⊥，M 为AB 的中点，D 为PB 的中点，且PMB ∆为正三角形.（1）求证：BC ⊥平面APC ；（2）若310BC AB ==，，求点B 到平面DCM 的距离.3．（补形法）将棱长为2的正方体1111ABCD A B C D -截去三棱锥1D ACD -后得到如图所示几何体，O 为11A C 的中点．（1）求证：//OB 平面1ACD ；（2）求几何体111ACB A D 的体积．4．（分割法）如图，矩形ABCD 中，3AB =，1BC =，E 、F 是边DC 的三等分点.现将DAE ∆、CBF ∆分别沿AE 、BF 折起，使得平面DAE 、平面CBF 均与平面ABFE 垂直.（1）若G 为线段AB 上一点，且1AG =，求证：DG 平面CBF ；（2）求多面体CDABFE 的体积.考法二：表面积1．如图，在四棱锥P ABCD -中，2AD =，1AB BC CD ===，//BC AD ，90PAD ∠=︒.PBA ∠为锐角，平面PAB ⊥平面PBD .（Ⅰ）证明：PA ⊥平面ABCD ；（Ⅰ）AD 与平面PBD ，求三棱锥P ABD -的表面积.2．如图，在直三棱柱111ABC A B C -中，AB BC ⊥，1222AA AB BC ===，M ，N ，D 分别为AB ，1BB ，1CC 的中点，E 为线段MN 上的动点.（1）证明：//CE 平面1ADB ；（2）若将直三棱柱111ABC A B C -沿平面1ADB 截开，求四棱锥1A BCDB -的表面积.3．如图,四棱锥P ABCD -中,底面ABCD 是菱形,PA ⊥平面ABCD ,3ABC π∠=,M 是PC 上一动点.（1）求证:平面PAC ⊥平面MBD ;（2）若PB PD ⊥,三棱锥P ABD -的体积为24求四棱锥P ABCD -的侧面积.考法三：求参数1．如图，在以A 、B 、C 、D 、E 、F 为顶点的五面体中，面ABCD 是等腰梯形，//AB CD ，面ABFE 是矩形，平面ABFE ⊥平面ABCD ，BC CD AE a ===，60DAB ∠=.（1）求证：平面⊥BDF 平面ADE ；（2）若三棱锥B DCF -a 的值.2．如图，在四棱锥P ABCD -中，PAD ∆是等边三角形，O 是AD 上一点，平面PAD ⊥平面,ABCD //,,1,2,3AB CD AB AD AB CD BC ⊥===.（1）若O 是AD 的中点，求证：OB ⊥平面POC ；（2）设=OD OAλ=，当λ取何值时，三棱锥B POC -考法四：求最值1．如图，在直三棱柱111ABC A B C -中，1AB =，2BC =，13,90,BB ABC =∠=点D 为侧棱1BB 上一个动点（1）求此直三棱柱111ABC A B C -的表面积；（2）当1AD DC +最小时，求三棱锥1D ABC -的体积.2．如图1，在矩形ABCD 中，2AB =，3BC =，点E 在线段BC 上，2BE EC =.把BAE ∆沿AE 翻折至1B AE ∆的位置，1B ∉平面AECD ，连结1B D ，点F 在线段1DB 上，12DF FB =，如图2.（1）证明：//CF 平面1B AE ；（2）当三棱锥1B ADE -的体积最大时，求二面角1B DE C --的余弦值.3．如图1，在边长为4的正方形ABCD 中，E 是AD 的中点，F 是CD 的中点，现将三角形DEF 沿EF 翻折成如图2所示的五棱锥P ABCFE -.（1）求证：AC 平面PEF ；（2）求五棱锥P ABCFE -的体积最大时PAC ∆的面积.4．如图，AB 是圆O 的直径，点C 是圆O 上异于,A B 的点，PO 垂直于圆O 所在的平面，且1PO =OB =．（Ⅰ）若D 为线段AC 的中点，求证C A ⊥平面D P O ； （Ⅰ）求三棱锥P ABC -体积的最大值；（Ⅰ）若BC =E 在线段PB 上，求CE OE +的最小值．。

第 1 页 共 18 页 2022年高考数学总复习：空间几何体的表面积与体积
1．多面体的表面积、侧面积
因为多面体的各个面都是平面，所以多面体的侧面积就是所有侧面的面积之和，表面积是侧面积与底面面积之和．
2．圆柱、圆锥、圆台的侧面展开图及侧面积公式 圆柱 圆锥 圆台
侧面展开图
侧面积公式
S 圆柱侧＝2πrl S 圆锥侧＝πrl S 圆台侧＝π(r 1＋r 2)l
3.柱、锥、台、球的表面积和体积
名称
几何体
表面积 体积 柱体(棱柱和圆柱)
S 表面积＝S 侧＋2S 底 V ＝Sh 锥体(棱锥和圆锥)
S 表面积＝S 侧＋S 底 V ＝13Sh 台体(棱台和圆台)
S 表面积＝S 侧＋S 上＋S 下 V ＝13(S 上＋S 下＋S 上S 下)h 球
S ＝4πR 2 V ＝43πR 3
知识拓展
1．与体积有关的几个结论
(1)一个组合体的体积等于它的各部分体积的和或差．
(2)底面面积及高都相等的两个同类几何体的体积相等．
2．几个与球有关的切、接常用结论
(1)正方体的棱长为a ，球的半径为R ，
①若球为正方体的外接球，则2R ＝3a ；
②若球为正方体的内切球，则2R ＝a ；
③若球与正方体的各棱相切，则2R ＝2a .
(2)若长方体的同一顶点的三条棱长分别为a ，b ，c ，外接球的半径为R ，则2R ＝a 2＋b 2＋c 2.。

空间几何体的表面积和体积【学习目标】1.通过对柱、锥、台体的研究，掌握柱、锥、台的表面积和体积的求法；2.能运用公式求解柱体、锥体和台体的体积，并且熟悉台体与柱体和锥体之间的转换关系；3.了解球的表面积和体积公式推导的基本思想，掌握球的表面积和体积的计算公式，并会求球的表面积和体积；4.会用柱、锥、台体和球的表面积和体积公式求简单几何体的表面积和体积.【要点梳理】【高清课堂：空间几何体的表面积和体积 395219 空间几何体的表面积】要点一、棱柱、棱锥、棱台的表面积棱柱、棱锥、棱台是多面体，它们的各个面均是平面多边形，它们的表面积就是各个面的面积之和．计算时要分清面的形状，准确算出每个面的面积再求和．棱柱、棱锥、棱台底面与侧面的形状如下表：要点诠释：求多面体的表面积时，只需将它们沿着若干条棱剪开后展开成平面图形，利用平面图形求多面体的表面积．要点二、圆柱、圆锥、圆台的表面积圆柱、圆锥、圆台是旋转体，它们的底面是圆面，易求面积，而它们的侧面是曲面，应把它们的侧面展开为平面图形，再去求其面积．1．圆柱的表面积（1）圆柱的侧面积：圆柱的侧面展开图是一个矩形，如下图，圆柱的底面半径为r，母线长l，那么这个矩形的长等于圆柱底面周长C=2πr，宽等于圆柱侧面的母线长l（也是高），由此可得S=C l=2πr l．圆柱侧（2）圆柱的表面积：2222()S r rl r r l πππ=+=+圆柱表． 2．圆锥的表面积（1）圆锥的侧面积：如下图（1）所示，圆锥的侧面展开图是一个扇形，如果圆锥的底面半径为r ，母线长为l ，那么这个扇形的弧长等于圆锥底面周长C=πr ，半径等于圆锥侧面的母线长为l ，由此可得它的侧面积是12S Cl rl π==圆锥侧．（2）圆锥的表面积：S 圆锥表=πr 2+πr l ．3．圆台的表面积（1）圆台的侧面积：如上图（2）所示，圆台的侧面展开图是一个扇环．如果圆台的上、下底面半径分别为r ＇、r ，母线长为l ，那么这个扇形的面积为π(r ＇+r)l ，即圆台的侧面积为S 圆台侧=π(r ＇+r)l ．（2）圆台的表面积：22('')S r r r l rl π=+++圆台表． 要点诠释：求旋转体的表面积时，可从旋转体的生成过程及其几何特征入手，将其展开后求表面积，但要搞清它们的底面半径、母线长与对应的侧面展开图中的边长之间的关系．4．圆柱、圆锥、圆台的侧面积公式之间的关系如下图所示．【高清课堂：空间几何体的表面积和体积395219 空间几何体的体积】 要点三、柱体、锥体、台体的体积1．柱体的体积公式棱柱的体积：棱柱的体积等于它的底面积S 和高h 的乘积，即V 棱柱=Sh ． 圆柱的体积：底面半径是r ，高是h 的圆柱的体积是V 圆柱=Sh=πr 2h ． 综上，柱体的体积公式为V=Sh ． 2．锥体的体积公式棱锥的体积：如果任意棱锥的底面积是S ，高是h ，那么它的体积13V Sh =棱锥．圆锥的体积：如果圆锥的底面积是S ，高是h ，那么它的体积13V Sh =圆锥；如果底面积半径是r ，用πr 2表示S ，则213V r h π=圆锥．综上，锥体的体积公式为13V Sh =．3．台体的体积公式棱台的体积：如果棱台的上、下底面的面积分别为S ＇、S ，高是h ，那么它的体积是1('')3V h S SS S =++棱台．圆台的体积：如果圆台的上、下底面半径分别是r ＇、r ，高是h ，那么它的体积是2211('')('')33V h S SS S h r rr r π=++=++圆台．综上，台体的体积公式为1('')3V h S SS S =++．4．柱体、锥体、台体的体积公式之间的关系如下图所示．【高清课堂：空间几何体的表面积和体积395219 球的体积与表面积】 要点四、球的表面积和体积 1．球的表面积（1）球面不能展开成平面，要用其他方法求它的面积． （2）球的表面积设球的半径为R ，则球的表面积公式 S 球=4πR 2．即球面面积等于它的大圆面积的四倍． 2．球的体积设球的半径为R ，它的体积只与半径R 有关，是以R 为自变量的函数．球的体积公式为343V R π=球．要点五、侧面积与体积的计算 1．多面体的侧面积与体积的计算在掌握直棱柱、正棱锥、正棱台侧面积公式及其推导过程的基础上，对于一些较简单的几何组合体的表面积与体积，能够将其分解成柱、锥、台、球，再进一步分解为平面图形（正多边形、三角形、梯形等），以求得其表面积与体积．要注意对各几何体相重叠部分的面积的处理，并要注意一些性质的灵活运用．（1）棱锥平行于底的截面的性质：在棱锥与平行于底的截面所构成的小棱锥中，有如下比例关系：S S S S S S ===小锥底小锥全小锥侧大锥底大锥全大锥侧对应线段（如高、斜高、底面边长等）的平方之比．要点诠释：这个比例关系很重要，在求锥体的侧面积、底面积比时，会大大简化计算过程．在求台体的侧面积、底面积比时，将台体补成锥体，也可应用这个关系式．（2）有关棱柱直截面的补充知识．在棱柱中，与各侧棱均垂直的截面叫做棱柱的直截面，正棱柱的直截面是其上下底面及与底面平行的截面．棱柱的侧面积与直截面周长有如下关系式：S 棱柱侧=C 直截l （其中C 直截、l 分别为棱柱的直截面周长与侧棱长）， V 棱柱=S 直截l （其中S 直截、l 分别为棱柱的直截面面积与侧棱长）． 2．旋转体的侧面积和体积的计算（1）圆柱、圆锥、圆台的侧面积分别是它们侧面展开图的面积，因此弄清侧面展开图的形式及侧面展开图中各线段与原旋转体的关系，是掌握它们的侧面积公式及解决有关问题的关键．（2）计算柱体、锥体和台体的体积，关键是根据条件找出相应的底面面积和高，要充分运用多面体的有关问题的关键．【典型例题】类型一、简单几何体的表面积例1．如右图，有两个相同的直三棱柱，高为2a，底面三角形的三边长分别为345(0)a a a a >、、．用它们拼成一个三棱柱或四棱柱，则a 的取值范围是 ．【答案】150a <<． 【解析】底面积为26a ，侧面面积分别为6、8、10，拼成三棱柱时，有三种情况：221262(1086)1248s a a =⨯+++=+， 222242(108)2436,s a a =++=+ 223242(106)2432,s a a =++=+拼成四棱柱时只有一种情况：表面积为22(86)2462428a a +⨯+⨯=+， 由题意得2224281248a a +<+，解得1503a <<． 【总结升华】（1）直棱柱的侧面积等于它的底面周长和高的乘积；表面积等于它的侧面积与上、下两个底面的面积之和．（2）求斜棱柱的侧面积一般有两种方法：一是定义法；二是公式法．所谓定义法就是利用侧面积为各侧面面积之和来求，公式法即直接用公式求解．举一反三：【变式1】 一个圆柱的底面面积是S ，侧面展开图是正方形，那么该圆柱的侧面积为（ ） A ．4S π B ．2S π C ．S π D ．23S π 【答案】A【解析】由圆柱的底面面积是S ，求出圆柱的半径为Sr π=，进一步求出侧面积为4S π．例2．在底面半径为R ，高为h 的圆锥内有一内接圆柱，求内接圆柱的侧面积最大时圆柱的高，并求此时侧面积的最大值．【思路点拨】一般要画出其轴截面来分析，利用相似三角形求解。

空间几何体的表面积和体积一．课标要求：了解球、棱柱、棱锥、台的表面积和体积的计算公式（不要求记忆公式）。

二．命题走向近些年来在高考中不仅有直接求多面体、旋转体的面积和体积问题，也有已知面积或体积求某些元素的量或元素间的位置关系问题。

即使考查空间线面的位置关系问题，也常以几何体为依托.因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式.同时也要学会运用等价转化思想，会把组合体求积问题转化为基本几何体的求积问题，会等体积转化求解问题，会把立体问题转化为平面问题求解，会运用“割补法”等求解。

由于本讲公式多反映在考题上，预测2009年高考有以下特色：（1）用选择、填空题考查本章的基本性质和求积公式；（2）考题可能为：与多面体和旋转体的面积、体积有关的计算问题；与多面体和旋转体中某些元素有关的计算问题；三．要点精讲1．多面体的面积和体积公式表中S表示面积，c′、c分别表示上、下底面周长，h表斜高，h′表示斜高，l表示侧棱长。

2．旋转体的面积和体积公式表中l、h分别表示母线、高，r表示圆柱、圆锥与球冠的底半径，r1、r2分别表示圆台上、下底面半径，R表示半径。

四．典例解析题型1：柱体的体积和表面积例1．一个长方体全面积是20cm 2，所有棱长的和是24cm ，求长方体的对角线长. 解：设长方体的长、宽、高、对角线长分别为xcm 、ycm 、zcm 、lcm 依题意得：⎩⎨⎧=++=++24)(420)(2z y x zx yz xy )2()1(由（2）2得：x 2+y 2+z 2+2xy+2yz+2xz=36（3）由（3）－（1）得x 2+y 2+z 2=16 即l 2=16所以l =4(cm)。

点评：涉及棱柱面积问题的题目多以直棱柱为主，而直棱柱中又以正方体、长方体的表面积多被考察。

我们平常的学习中要多建立一些重要的几何要素（对角线、内切）与面积、体积之间的关系。

例2．如图1所示，在平行六面体ABCD —A 1B 1C 1D 1中，已知AB=5，AD=4，AA 1=3，AB ⊥AD ，∠A 1AB=∠A 1AD=3π。

2020年高考数学二轮复习专项微专题核心考点突破专题23立体几何中的表面积与体积综观近几年的全国卷，空间几何体的表面积与体积计算是常考内容，一般文、理科各考一道小题（5分）和文科一道解答题其中的一个小问（6分）.文科较理科更偏重于几何体的表面积与体积计算.再进一步研究相关的试题，不难看出，对几何体表面积与体积的考查，已由原来的简单几何体的直接套用公式，逐步演变为三视图或折叠图或柱体、锥体、台体和球等相结合的组合体的表面积与体积计算，难度在增大，而且这种演化的趋势依然存在.所以，笔者预计后续几年的高考中，对这部分内容的考查仍然会延续以上的命题思路与特点，围绕三视图、折叠图及非规则组合体方面会进一步探索，创新命题设计.因此，我们在复习备考中，首先要加强研究，注意总结规律和方法，尤其是通性通法；其次要强化训练，熟练掌握和运用这些通性通法，做到以不变应万变，提高学生应对此类问题的能力和水平^1以三视图为载体的几何体表面积与体积计算用三视图呈现空间几何体的结构特征及度量关系，打破了以往直接给出空间几何体的直观图及相关数据进行计算的传统模式，化立体为平面，加大了几何体的空间想象难度，对学生的空间想象、模型构建及运算求解等提出了较高要求.例1某多面体的三视图如图1所示，其中正视图和侧视图都由正方形和等腰直角三角形组成，正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（）A.10B.12C.14D.16思路探求：该题重点考查学生对三视图的分析能力，并能从三视图中发现几何体各元素之间的位置关系和数量关系，构建出空间直观图，进而求得几何体的有关面积.所以，如何正确地根据三视图还原出空间直观图是解决问题的关键.本题中所给三视图的正视图、侧视图由两部分组成，可推测直观图是组合体.又由俯视图只有一个图形，推测直观图是上下组合结构的 .再由正视图、侧视图上半部分和俯视图均为等腰直角三角形,可推断直观图上半部分是三棱锥；由正视图、侧视图下半部分是正方形和俯视图是等腰直角三角形，可推 断直观图下半部分是直三柱 .因此可以断定，该几何体的直观图是由一个三棱锥和三棱柱构成，并且各面内 只有两个侧面是相同的梯形，面积之和为2XCZ + 4）X2X ： = 12 .故选B变式1如图所示，网格纸上小正方形的边长为 1,粗实线画出的是某几何体的三视图，该几何体由一平面将圆柱截去一部分后所得，则该几何体的体积为思路探求：三视图是由一个平面将一个圆柱截去一部分后所得几何体的三视图，其还原为实际形状时，是一个上下组合的几何体.下半部分是一个底面半径为 3、高为4的圆柱，其体积％ = TE 巽第X 4 = 3丽；上半部 分是一个底面半径为3、高为6的圆柱的一半，其体积 K = ；x （irx33x5） =27室，故该组合体的体积7 = 一―% = 36兀-27雇=白演.故选B方法点睛：解决以三视图为载体的几何体度量计算问题，关键是要根据三视图准确还原出几何体的空间直观 图.要做到准确还原，我们需要抓住三视图与直观图的对应关系，首先确定空间几何体是简单几何体 （或简单几何体上的切割、挖补）还是组合体，是多面体还是旋转体；然后再根据 长对正，宽相等，高平齐 ”的对应法则确定几何体中各个量的大小；最后准确还原出空间几何体的直观图 ^从例1和变式1的分析过程，我们会发现，对于非规则几何体（或组合体）的三视图的还原过程，其中简单几何体是作为一个整体构件来运用的，非规则几何体是由简单的几何体按一定方式组合而成的.因此，熟练掌握简单几何体柱、锥、台、球等结构特征以及三视图与直观图之间的对应联系，是解决非规则几何体三视 图问题的前提和基础.因此，在教学中教师要引导学生加强简单几何体各种位置的三视图与直观图的识图、 画图、用图等基本功的训练 .2与球有关的几何体的表面积与体积计算球是一个非常完美的几何体，自身有很好的对称性.因此，从球体本身就可以挖掘出许多几何关系和度量计算进行问题设计.此外，由于球自身的完美性质，人们常常将它与其他简单的几何体柱、锥、台等，通过内一J r O 9_里切或外接的方式组合成新的几何体，使其能够更加深入地考查空间几何关系与度量计算.因此，球也是高考立体几何命题的一个重要资源 .例2已知三棱锥f - 484的所有顶点都在球O的球面上，SC是球O的直径若平面SCA，平面SCB, SA=AC, SB=BC,三棱锥SABC的体积为9,则球。