北师大版勾股定理的应用
- 格式:doc
- 大小:159.50 KB
- 文档页数:5










勾股定理的应用(一)1.勾股定理的应用(1)在不规则的几何图形中,通常添加辅助线得到直角三角形.(2)在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.(3)常见的类型:①勾股定理在几何中的应用:利用勾股定理求几何图形的面积和有关线段的长度.①由勾股定理演变的结论:分别以一个直角三角形的三边为边长向外作正多边形,以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和.①勾股定理在实际问题中的应用:运用勾股定理的数学模型解决现实世界的实际问题.①勾股定理在数轴上表示无理数的应用:利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.例题精讲知识点一利用勾股定理列出方程求线段长度的应用例1.如图1-1,在①ABC中,AB=15,BC=14,CA=13,求BC边上的高AD.训练3-1.①ABC中,①ACB=90°,CD是高,若AB=13cm,AC=5cm,则CD的长为___________.训练1-2.如图,在钝角△ABC中,BC=9,AB=17,AC=10,AD⊥BC于D,求AD的长.知识点二、勾股定理在实际中的应用(注意列方程的思想解答)勾股定理在生活中的应用三步走:1、学会设未知数x;2、利用题目条件尽量去表示出相关的边长;3、寻找一个合适的三角形使用勾股定理列方程;例题2.一个长方形池塘的池深与池宽相等,如图,有一颗芦苇长在塘中央,露出水面1m,把芦苇顶拉到岸边,刚好与水面齐平,求水深和芦苇的长度(结果可保留根号),你能解决这个问题吗?训练2-1.在一棵树的10米高的B处有两只猴子.一只猴子爬下树走到离树20米的池塘的A处.另一只爬到树顶D后直按跃到A处.距离以直线计算.如果两只猴子所经过的距离相等.则这棵树高多少米?训练2-2.如图,旗绳自由下垂时,比旗杆长1米,如果将旗绳斜拉直,下端在地面上,距旗杆底部5米,求旗杆的高度.知识点三、滑梯问题例题3.如图所示,一架长10m的梯子AB斜靠在与地面OM垂直的墙壁ON上,AO长度是8m;(1)求BO的长;(2)若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行,如图2所示,设A点下滑到C点,B点向右滑行到D点,并且BD=1m,试计算梯子顶端A沿NO下滑多少米.例题4.如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点.当它靠在另一侧墙上时,梯子的顶端在D点,已知梯子长2.5m,D点到地面的垂直距离DE=1.5m,两墙的距离CE长3.5m.求B点到地面的垂直距离BC.综合应用1.有两棵树,一棵高7米,另一棵高2米,两树相距12米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,求小鸟至少需要飞多少米.2.如图.公路AB的同侧有两所学校C、D,学校D到公路的距离DA=3km,学校C到公路的距离CB=2km,已知AB=5km.现在要在公路AB上建一个公交车站E,使车站E 到学校C、D的距离相等,则AE为多少?3.如图,为了求出湖两岸的A、B点之间的距离,一个观测者在点C设桩,使三角形ABC 恰好为直角三角形,通过测量,得到AC长160米,BC长128米,问从点A穿过湖到点B有多远?解:在Rt△ABC中,∠=90°,由勾股定理得,AB2+BC2=AC2∴AB2=()2﹣()2=()2﹣()2=∴AB=(米)答:从点A穿过湖到点B有米.ABCDEFAE BCDF 勾股定理的应用(二)翻折问题的应用知识点一 翻转折叠问题1、翻折问题的实质是全等,寻找相等线段和相等角度;2、设X; 并且表示出相关边长;3、在合适的三角形中,用勾股定理列方程;例1.如图,小红用一张长方形纸片ABCD 进行折纸,已知该纸片宽AB 为8cm ,•长BC•为10cm .当小红折叠时,顶点D 落在BC 边上的点F:处(折痕为AE )(1)求BF 的长; (2)求EC 的长.训练1-1.如图,折叠长方形的一边BC ,使点B 落在AD 边的F 处,已知:AB=3,BC=5,求折痕EF 的长.训练1-2.如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝.现将直角边AC沿直线AD折叠,使它落在斜边AB上,恰与AE重合,求CD的长度.训练1-3.如图所示,有一块直角三角形纸片,∠C=90°,AC=4 cm,BC=3 cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长是多少?例题2.如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,若AB=6,BC=9,则BF的长为多少?训练2-1.如图,将一个边长分别为4、8的长方形纸片ABCD折叠,使C点与A点重合,求EB的长.ACDBEFEDCBA训练2-2..如图,长方形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B在点F处,折痕为AE,且EF=3,则AB的长为多少?训练2-3.如图,在长方形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为多少?综合应用1.如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为________.2.如图,在Rt△ABC中,∠C=90°,BC=6 cm,AC=8 cm,按图中所示方法将△BCD沿BD 折叠,使点C落在AB边的C′点,那么△ADC′的面积是________.3.如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8,将它的锐角A翻折,使得点A落在BC边的中点D处,折痕交AC边于点E,交AB边于点F,则DE的值为________.4.如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC 上,与点B′重合,AE为折痕,则EB′=________.5.为了向建国六十六周年献礼,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20 cm,宽AB=16 cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,请你根据①②步骤解答下列问题:计算EC,FC的长.。
勾股定理的应用
知识梳理:
勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决.
题型一、关于路线最短问题
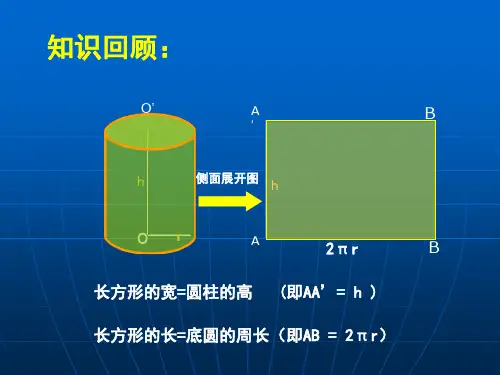
例1、有这样一个有趣的问题:如图所示,有一个圆柱,它的高等于12cm,底面半径等于3cm。
在圆柱的下底面的A点有一只蚂蚁,它想吃到上底面上与A相对的B点的食物,需要沿圆柱的侧面爬行的最短路程是多少( 的值取3)
注:这个问题最终的解决,是把圆柱的侧面沿着它的一条母线剪开展成一个长方形,从而把曲面上的路线问题转化为平面上A、B两点间的路线问题。
像这种,将空间问题转化为平面问题的方法,对发展我们的空间观念是很有好处的。
牛刀小试:
1、一个无盖的长方体形盒子的长、宽、高分别为8cm,8cm,12cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,你能帮蚂蚁设计一条最短的路线吗蚂蚁要爬行的最短行程是多少
B
12
8
A 8
题型二、测量实际距离(求线段长度)
例2、在某一平地上,有一棵树高8米的大树,一棵树高3米的小树,两树之间相距12米。
今一只小鸟在其中一棵
树的树梢上,要飞到另一棵树的树梢上,问它飞行的最短距离是多少
小试牛刀:
.2.如图,某沿海开放城市A 接到台风警报,在该市正南方向100km 的B 处有一台风中心,沿BC 方向以20km/h 的速度向D 移动,已知城市A 到BC 的距离AD=60km ,那么台风中心经过多长时间从B 点移到D 点如果在距台风中心30km 的圆形区域内都将有受到台风的破坏的危险,正在D 点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险
课堂巩固:
1、有一圆柱体高为10cm ,底面圆的半径为4cm ,AA 1、BB 1为相对的两条母线。
在AA 1上有
一个蜘蛛Q ,QA =3cm ;在BB 1上有一只苍蝇P ,PB 1=2cm 。
蜘蛛沿圆柱体侧面爬到P 点吃苍蝇,最短的路径是 cm 。
(π 3)
2. 如图是一个长方体长4、宽3、高12,则图 中阴影部分的三角形的周长为__________
3. 如图,一架米长的梯子AB ,斜靠在一竖直的墙AC 上,这时梯足B 到墙底端C 的距离为米,如果梯子的顶端沿墙下滑米,那么梯足将向外移多少米
第2题 12 A
B 1 A 1 B
Q P
A
B
C
D
A 1
B A
课后练习:
一.选择题
1.下列四组数据不能作为直角三角形的三边长的是( ) A .6、8、10 、12、13 、18、22 、12、15
2.如图:正方形A 的面积为36,正方形B 的面积为64,则正方形C 的面积为( )
3.一个直角三角形的一条直角边长为12cm,斜边长为15cm,则此直角三角形的面积为( ) cm
2
cm
2
cm
2
cm
2
4.将直角三角形的三条边同时扩大4倍后,得到的三角形为( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定
5.等腰三角形的一腰长为13,底边长为10,则它的面积为( )
6.如右图:已知AD 是△ABC 的高,AB=10,AD=8,BC=12,则△ABC 为( ) A.等腰三角形 B.等腰直角三角形 C.直角三角形 D.不能确定
7.等边三角形的边长是10,它的高的平方等于( ) 8.三角形三边长分别为a
2
-b
2
、2ab 、a
2
+b
2
(a >b >0),则这个三角形为( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.不是直角三角形
9.已知:如图,在△ABC 中,D 是AC 的中点,∠C=90°,下列等式不成立的为( )
2
+BC
2
=AB
2
2
+BC
2
=BD
2
2
+BC
2
=BD
2
2
+BD
2
=AB
2
10. 在直角三角形ABC 中,斜边AB =2,则2
2
2
AB AC BC ++=______. 11 直角三角形的三边长为连续偶数,则其周长为 .
12. 如图,在△ABC 中,∠C=90°,BC=3,AC=4.以斜边AB 为直径作半圆,则这个半圆的面积是____________.
(第13题) (第14题) (第15题) 13. 如图,校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵
树的顶端,小鸟至少要飞___________米.
14. 如图,△ABC 中,∠C =90°,AB 垂直平分线交BC 于D 若BC =8,AD =5,则AC 等于______________. 15. 如图,四边形ABCD 是正方形,AE 垂直于BE ,且AE =3,BE =4,阴影部分的面积是______.
16. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为7cm,则正方形A ,B ,C ,D 的面积之和为___________cm 2
.
二、解答题
1、甲、乙两位探险者到沙漠进行探险。
某日早晨8:00甲先出发,他以6千米/时的速度向正东行走。
1小时后乙出发,他以5千米/时的速度向正北行走。
上午10:00,甲、乙二人相距多远
2、如图所示,某地有A,B,C 三个村庄,C 村到B 村,A 村的距离分别为24千米,10千米,A,B 两村相距26千米,现要从C 村修一公路CD 到AB ,要求所修公路最短,请你在图上标出D 点的位置,并求出CD 的长。
A
B
D
E A B C D
第
16题图
7cm
3、如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积。