全等三角形角边角判定的基本练习

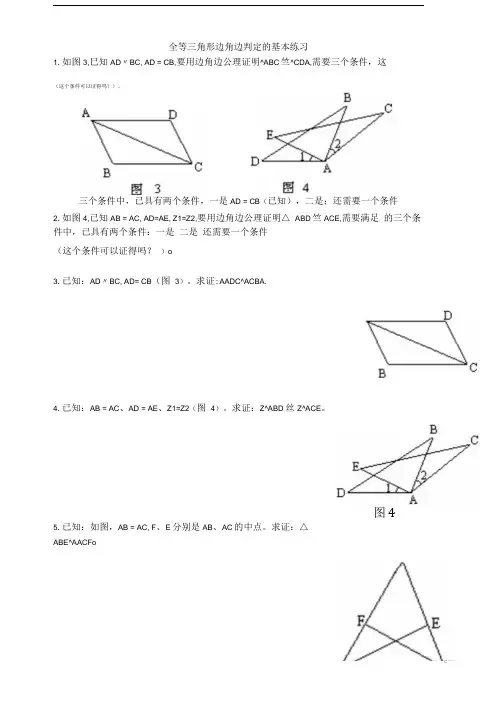
（这个条件可以证得吗？）。

全等三角形边角边判定的基本练习1.如图3,巳知AD〃BC, AD = CB,要用边角边公理证明^ABC竺^CDA,需要三个条件，这三个条件中，已具有两个条件，一是AD = CB（已知），二是；还需要一个条件2.如图4,已知AB = AC, AD=AE, Z1=Z2,要用边角边公理证明△ ABD竺ACE,需要满足的三个条件中，已具有两个条件：一是二是还需要一个条件（这个条件可以证得吗？）o3.已知：AD〃BC, AD= CB（图3）。

求证:AADC^ACBA.4.已知：AB = AC、AD = AE、Z1=Z2（图4）。

求证：Z^ABD 丝Z^ACE。

图45.已知：如图，AB = AC, F、E分别是AB、AC的中点。

求证：△ABE^AACFoC6、己知：点A、F、E、C 在同一条直线上，AF = CE, BE〃DF, BE = DF. 求证：△ABE#ACDF.D C7、已知：如图AB=AC,AD=AE,ZBAC= ZDAE,求证：AABD^AACE8、如图，ZiABC中，AB = AC, AD平分匕BAC,试说明^ABD丝MCD。

B D C9、已矢口：如图，AD〃BC, AD=CB 。

求证：AADC^ACBAo，AD±11、已知：如图，点A、B、C、D在同一条直线上，DB=,垂足分别是A、Do求证：△FDCWA13、如图，在中，D是AB ±一点，DF交AC于点E, FE= , CE= , AB与CF 有什么位置关系？说明你判断的理由。

12、己知：如图，AC= ， AE= ,Z1=Z2A14、己知：如图，ZDBA=Z ， BD= ° 求证ZC=ZD15、已知：如图，AC和BD相交于点0, 0C= , 0D= 。

求证：DC〃AB。

16、已知：如图，AC和BD相交于点0, DC= ， DB= 0求证：ZC=ZB17、已知：如图,D、E分别是^ABC的边AB,AC的中点，点F在DE的延长线上，且EF=DE. 求证：(1)BD=FC (2)AB〃CFB C18、己知：如图,AB=AC, EB=EC, AE的延长线交BC于D.求证：BD=CD19、已知:如图,AB=AC,AD=AE,ZBAC= ZDAE.求证:BD=CE20、已知，AABC和AECD都是等边三角形，且点B, C, D在一条直线上求证：BE=AD21、如图，己知，AB〃DE, AB=DE, AF=DCo请问图中有那儿对全等三角形？请任选一对给予证明。

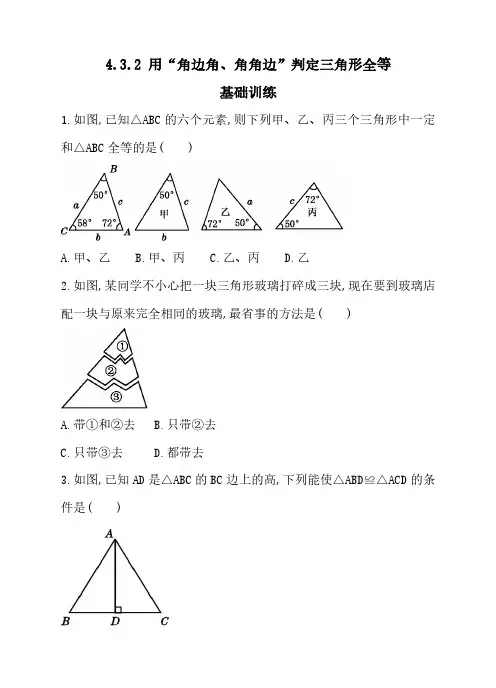
4.3.2 用“角边角、角角边”判定三角形全等基础训练1.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中一定和△ABC全等的是( )A.甲、乙B.甲、丙C.乙、丙D.乙2.如图,某同学不小心把一块三角形玻璃打碎成三块,现在要到玻璃店配一块与原来完全相同的玻璃,最省事的方法是( )A.带①和②去B.只带②去C.只带③去D.都带去3.如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )A.∠BAD=∠CADB.∠BAC=99°C.BD=ACD.∠B=45°4.如图,已知∠A=∠D,∠1=∠2,那么要得到△ABC≌△DEF,还应给出的条件可以是( )A.∠E=∠BB.ED=BCC.AB=EFD.AF=CD5.下列条件中,能判定△ABC≌△DEF的是( )A.AB=DE,BC=EF,∠A=∠EB.∠A=∠E,AB=EF,∠B=∠DC.∠A=∠D,∠B=∠E,∠C=∠FD.∠A=∠D,∠B=∠E,AC=DF6.根据图中所给条件,能够判定哪两个三角形全等?( )A.①和②B.②和④C.①和③D.③和④7.如图,AB∥CD,且AB=CD,则△ABE≌△CDE的根据是( )A.只能用ASAB.只能用SSSC.只能用AASD.用ASA或AAS8.如图,∠1=∠2,∠3=∠4,OE=OF,则图中全等的三角形有( )A.1对B.2对C.3对D.4对9.如图,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( )A.1个B.2个C.3个D.4个10.如图,已知∠B=∠ACD,∠ACB=∠D=90°,AC是△ABC和△ACD的公共边,所以就可以判定△ABC≌△ACD.你认为这种说法正确吗?如果不正确,请说明理由.提升训练11.如图,在四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.试说明:△ABC与△DEC全等.12.如图,已知∠CAB=∠DBA,∠CBD=∠DAC.　试说明:BC=AD.13.如图①,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.(1)试说明:MN=AM+BN.(2)如图②,若过点C作直线MN与线段AB相交,AM⊥MN于点M,BN⊥MN 于点N(AM>BN),(1)中的结论是否仍然成立?说明理由.14.我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.试说明:OE=OF.参考答案1.【答案】C2.【答案】C3.【答案】A4.【答案】D5.【答案】D6.【答案】D7.【答案】D　8.【答案】B　9.【答案】C10.错解:正确.诊断:用“AAS”判定两个三角形全等时,这两组角与一对边不是仅仅“相等”就可以了,而必须是“对应相等”,即两个三角形中相等的边和角必须有相同的顺序.在△ABC中,AC是锐角∠B的对边,而在△ACD中,AC却是直角∠ADC 的对边,它们之间不存在“对应相等”的关系.正解:不正确.理由:因为AC 虽然是△ABC 和△ACD 的公共边,但不是对应边.11.解:如图,因为∠BCE=∠ACD=90°,所以∠3+∠4=∠4+∠5.所以∠3=∠5.在△ACD 中,∠ACD=90°,所以∠2+∠D=90°.因为∠BAE=∠1+∠2=90°,所以∠1=∠D.在△ABC 和△DEC 中,{∠1=∠D ,∠3=∠5,BC =EC ,所以△ABC ≌△DEC.12.解:因为∠CAB=∠DBA,∠CBD=∠DAC,所以∠DAB=∠CBA.在△ADB 与△BCA 中{∠DBA =∠CAB ,AB =AB ,∠DAB =∠CBA ,所以△ADB ≌△BCA(ASA).所以BC=AD.13.解:(1)因为∠ACB=90°,所以∠ACM+∠BCN=90°.又因为AM ⊥MN,BN ⊥MN,所以∠AMC=∠CNB=90°.所以∠BCN+∠CBN=90°.所以∠ACM=∠CBN.在△ACM 和△CBN 中,{∠ACM =∠CBN ,∠AMC =∠CNB ,AC =BC ,所以△ACM ≌△CBN(AAS).所以MC=NB,MA=NC.因为MN=MC+CN,所以MN=AM+BN.(2)(1)中的结论不成立,结论为MN=AM-BN.理由如下:同理可得△ACM ≌△CBN(AAS),所以CM=BN,AM=CN.因为MN=CN-CM,所以MN=AM-BN.14.解:因为在△ABD 和△CBD 中,{AB =CB ,AD =CD ,BD =BD ,所以△ABD ≌△CBD(SSS).所以∠ABD=∠CBD.又因为OE⊥AB,OF⊥CB,所以∠OEB=∠OFB.在△BOE和△BOF中,{∠EBO=∠FBO,∠OEB=∠OFB,OB=OB,所以△BOE≌△BOF(AAS).所以OE=OF.。

全等三角形的判定练习题全等三角形在几何学中是一个重要的概念。

判定两个三角形是否全等是解决几何问题的基础，也是推导其他几何性质的前提。

本文将提供一些全等三角形的判定练习题，以帮助读者巩固和加深对该概念的理解。

练习题1：已知三角形ABC和DEF，判定它们是否全等。

已知如下条件：1. ∠A = ∠D，∠B = ∠E，∠C = ∠F；2. AB = DE，BC = EF，AC = DF。

解析：根据题目给出的条件，我们可以得出以下结论：1. 两个三角形的对应角度相等（∠A = ∠D，∠B = ∠E，∠C =∠F）；2. 两个三角形的对应边长相等（AB = DE，BC = EF，AC = DF）。

由于两个三角形的对应角度和对应边长都相等，因此可以判定三角形ABC和DEF全等。

练习题2：已知三角形ABC和DEF，判定它们是否全等。

已知如下条件：1. ∠A = ∠D，∠B = ∠E；2. AB = DE，AC = DF。

解析：根据题目给出的条件，我们可以得出以下结论：1. 两个三角形的对应角度相等（∠A = ∠D，∠B = ∠E）；2. 两个三角形的对应边长不全等（AB = DE，AC = DF）。

由于两个三角形仅仅只有两对对应角度相等且没有所有对应边长相等，因此无法判定三角形ABC和DEF全等。

练习题3：已知三角形ABC和DEF，判定它们是否全等。

已知如下条件：1. ∠A = ∠D，∠B = ∠E，∠C = ∠F；2. AB = DE，AC ≠ DF。

解析：根据题目给出的条件，我们可以得出以下结论：1. 两个三角形的对应角度相等（∠A = ∠D，∠B = ∠E，∠C =∠F）；2. 两个三角形的对应边长不全等（AB = DE，AC ≠ DF）。

由于两个三角形仅仅只有三对对应角度相等且没有所有对应边长相等，因此无法判定三角形ABC和DEF全等。

通过以上练习题，我们可以发现判定两个三角形是否全等时，既需要考虑对应角度是否相等，又需要考虑对应边长是否相等。

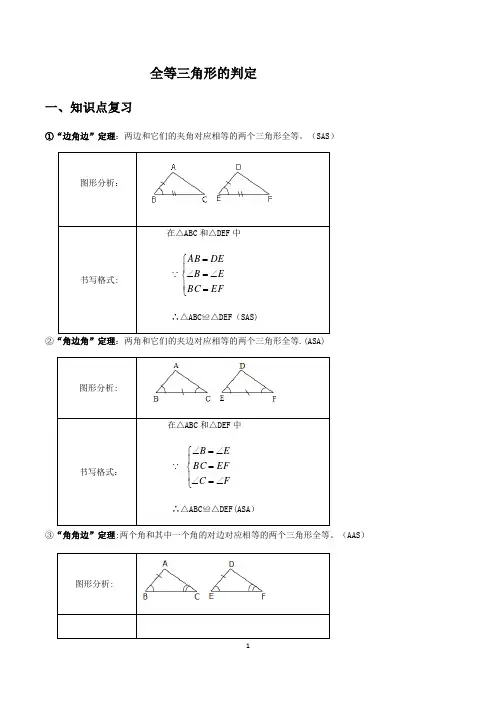
全等三角形的判定一、知识点复习①“边角边”定理：两边和它们的夹角对应相等的两个三角形全等。

（SAS）图形分析：书写格式: 在△ABC和△DEF中⎪⎩⎪⎨⎧=∠=∠=EFBCEBDEAB∴△ABC≌△DEF（SAS)②“角边角”定理：两角和它们的夹边对应相等的两个三角形全等.(ASA)图形分析:书写格式：在△ABC和△DEF中⎪⎩⎪⎨⎧∠=∠=∠=∠FCEFBCEB∴△ABC≌△DEF(ASA）③“角角边”定理:两个角和其中一个角的对边对应相等的两个三角形全等。

（AAS）图形分析:书写格式： 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧=∠=∠∠=∠EF BC F C E B∴△ABC ≌△DEF （AAS)④“边边边”定理：三边对应相等的两个三角形全等.(SSS ）图形分析：书写格式： 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧===EF BC DF AC DE AB∴△ABC ≌△DEF(AAS)⑤“斜边、直角边”定理：斜边和一条直角边对应相等的两个直角三角形全等。

(HL ）图形分析：书写格式：在△ABC 和△DEF 中⎩⎨⎧==DF AC DE AB ∴△ABC ≌△DEF （HL ）一个三角形共有三条边与三个角，你是否想到这样一问题了：除了上述四种识别法,还有其他的三角形全等识别法吗?比如说“SSA ”、“AAA ”能成为判定两个三角形全等的条件吗？两个三角形中对应相等的元素两个三角形是否全等 反例SSA ⨯AAA⨯二、常考典型例题分析第一部分：基础巩固1。

下列条件,不能使两个三角形全等的是（ ）A ．两边一角对应相等B ．两角一边对应相等C ．直角边和一个锐角对应相等D ．三边对应相等2.如图，点D ，E 分别在线段AB ，AC 上,CD 与BE 相交于O 点，已知AB=AC ，现添加以下的哪个条件仍不能判定△ABE ≌△ACD( )A.∠B=∠C B．AD=AE C．BD=CE D．BE=CD3。

14.4（2）全等三角形的判定ASA、AAS一、探究现在，我们讨论：如果两个三角形有两个角、一条边分别对应相等，那么这两个三角形能全等吗？这时同样应有两种不同的情况：如图所示，一种情况是两个角及这两角的夹边；另一种情况是两个角及其中一角的对边．ASA AAS二、检测反馈，学以致用1.如图，已知AO=DO，∠AOB与∠DOC是对顶角，还需补充条件______________=_______________，就可根据“ASA”说明△AOB≌△DOC；或者补充条件_______________=_______________，就可根据“AAS”，说明△AOB≌△DOC。

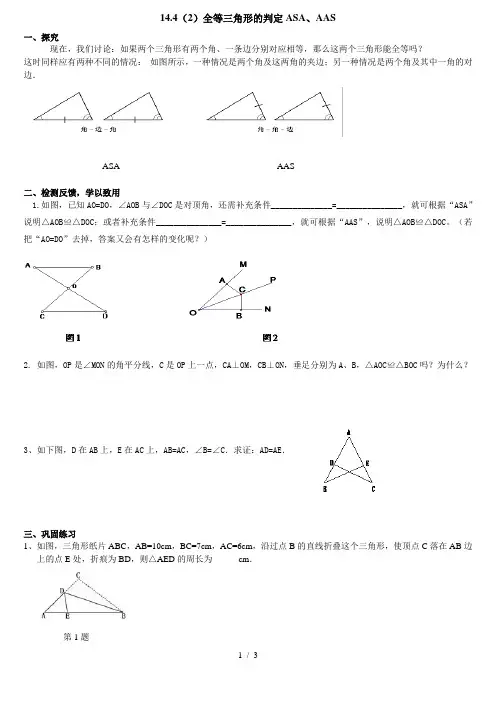
（若把“AO=DO”去掉，答案又会有怎样的变化呢？）2. 如图，OP是∠MON的角平分线，C是OP上一点，CA⊥OM，CB⊥ON，垂足分别为A、B，△AOC≌△BOC吗？为什么？3、如下图，D在AB上，E在AC上，AB=AC，∠B=∠C．求证：AD=AE．三、巩固练习1、如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为______cm．第1题2、已知：如图 , ∠1=∠2 , ∠3=∠4求证：AC=AB．3．如图，AB⊥BC，AD⊥DC，∠BAC=∠CAD.试说明：AB=AD .4、已知：如图 , FB=CE , AB∥ED , AC∥FD.F、C在直线 BE上．求证：AB=DE , AC=DF．5、如图，在△ABC中，∠C=2∠B,AD是△ABC的角平分线，∠1=∠B,试说明：AB=AC+AD6、已知：如图，AB=DC，∠A=∠D．试说明：∠1=∠2．7.如图，ΔABC中，D是AC上一点，BE∥AC，BE=AD，AE分别交BD、BC于点F、G．⑴图中有全等三角形吗？请找出来，并证明你的结论．⑵若连结DE，则DE与AB有什么关系？并说明理由．。

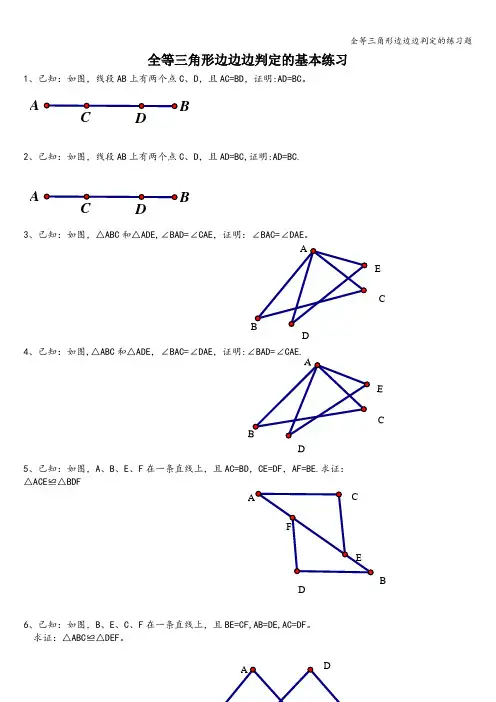
全等三角形边边边判定的基本练习
1、已知：如图，线段AB上有两个点C、D，且AC=BD，证明:AD=BC。

A B
2、已知：如图，线段AB上有两个点C、D，且AD=BC,证明:AD=BC.
A B
3、已知：如图，△ABC和△ADE,∠BAD=∠CAE，证明：∠BAC=∠DAE。

4、已知：如图,△ABC和△ADE，∠BAC=∠DAE，证明:∠BAD=∠CAE.
5、已知：如图，A、B、E、F在一条直线上，且AC=BD，CE=DF，AF=BE.求证：△ACE≌△BDF
6、已知：如图，B、E、C、F在一条直线上，且BE=CF,AB=DE,AC=DF。

求证：△ABC≌△DEF。

E
D C
E
D C
D
B
7、如图，△ABC 中,D 是BC 边的中点，AB=AC ，求证：∠B=∠C 。

8、已知:如图，AB=DC ，AD=BC ，求证：∠A=∠C.
9、已知：如图 , AB=AC , AD=AE , BD=CE ．求证：∠BAC=∠DAE ．
D
C
B
D
C
B
B
C
A
8、这个世界并不是掌握在那些嘲笑者的手中，而恰恰掌握在能够经受得住嘲笑与批忍不断往前走的人手中。

9、障碍与失败，是通往成功最稳靠的踏脚石,肯研究、利用它们，便能从失败中培养出成功。

10、在真实的生命里，每桩伟业都由信心开始，并由信心跨出第一步。

全等三角形的判定方法50道经典题摘要：1.全等三角形的判定方法概述2.边边边（SSS）判定法3.边角边（SAS）判定法4.角边角（ASA）判定法5.角角边（AAS）判定法6.斜边，直角边（HL）判定法7.经典题型一：已知三边长度，判断全等8.经典题型二：已知两边和夹角，判断全等9.经典题型三：已知两角和夹边，判断全等10.经典题型四：已知两边和等角对边相等，判断全等11.经典题型五：已知斜边和直角边，判断全等12.经典题型六：综合运用判定法，判断全等13.解题技巧与注意事项14.巩固练习：50道经典题解答与解析正文：全等三角形的判定方法是数学中非常重要的内容，掌握判定方法有助于解决许多实际问题。

本文将详细介绍全等三角形的判定方法，并通过50道经典题进行巩固练习。

1.全等三角形的判定方法概述全等三角形判定方法有六种，分别为：边边边（SSS）、边角边（SAS）、角边角（ASA）、角角边（AAS）、斜边，直角边（HL）。

2.边边边（SSS）判定法当两个三角形的三条边分别对应相等时，这两个三角形全等。

例如，若给出三条线段长度ABc，BCa，ACb，我们可以通过以下步骤确定全等三角形：步骤一：确定一边AB。

步骤二：分别以AB为圆心，做半径为b，a长的圆，交于点C。

步骤三：连接AC，BC。

这样，三角形的大小和形状就都被确定出来。

3.边角边（SAS）判定法当两个三角形的两边和它们的夹角分别相等时，这两个三角形全等。

例如，已知ABc，CAB，我们可以通过以下步骤确定全等三角形：步骤一：画射线AE，并在射线AE上截取ACc。

步骤二：在射线AD上截取ABc。

步骤三：连接BC。

这样，三角形的大小和形状就都被确定出来。

4.角边角（ASA）判定法当两个三角形的两个角和它们的夹边分别相等时，这两个三角形全等。

例如，已知ABc，CAB，我们可以通过以下步骤确定全等三角形：步骤一：先确定一边ABc。

步骤二：在AB同旁画DAB，EBA，AD，BE交于点C。