§7.2近似数和有效数字 贺同明 临朐四中
- 格式:ppt
- 大小:1.05 MB
- 文档页数:11

多边形及其内角和、梯形【知识梳理】1. 多边形内角和,外角和,对角线2. 正多边形的内切圆和外接圆3.利用三角形、四边形或正六边形进行简单的镶嵌设计【思想方法】解决此类问题时要注重观察、操作、猜想、探究等活动过程,注重知识的理解和运用.【例题精讲】例题 1.一个多边形,它的每个内角都等于相邻外角的5倍,则这个多边形是( )A . 正五边形B . 正十边形C .正十二边形D .不存在.例题2.只用一种正多边形进行镶嵌,在下列的正多边形中,不能镶嵌成一个平面的是( ).A .正三角形 B.正方形 C.正五边形 D.正六边形例题3.(1)n 边形的内角和等于 ,多边形的外角和都等于 .(2)一个多边形的内角和等于它的外角和,那么这个多边形是 边形.(3)一个多边形的每个外角都是300, 则这个多边形是 边形.(4)一个十边形所有内角都相等,它的每一个外角等于 度.(5)一个五边形五个外角的比是2:3:4:5:6,则这个五边形五个外角的度数分别是 .(6)多边形边数增加一条,则它的内角和增加 度,外角和例题 4.半径为2的圆的内接正六边形边长为_______,外切正三角形的边长为__________.例题5.如图,四边形ABDC 中,120ABD ∠=°,AB AC ⊥,BD CD ⊥,4AB CD ==,,则该四边形的面积是 .例题6.一个多边形的外角和是内角和的15,它是几边形?例题7.一个多边形每一个外角都等于与它相邻的内角,这种多边形是几边形?例题8.五角星图案中间部分的五边形ABCDE 是一个正五边形,则图中∠ABC的度数是多少?【当堂检测】 1.填空:(1)n 边形的内角和为720°,则n =______.(2)五边形的内角和与外角和的比值是______.A BDC(3)过六边形的每一个顶点都有______条对角线.(4)过七边形的一个顶点的所有对角线把七边形分成______个三角形.(5)将正六边形绕其对称中心O旋转后,恰好能与原来的正六边形重合,那么旋转的角度至少是度.2.一个多边形的内角和是外角和的2倍,则这个多边形的边数为()A.4 B.5 C.6 D.73.只用下列正多边形地砖中的一种,能够铺满地面的是()A.正十边形B.正八边形C.正六边形D.正五边形4.一个五边形有三个内角是直角,另两个内角都等于n,则n的值是A.30°B.120°C.135°D.108°5.n边形与m边形内角和度数差为720°,则n与m的差为()A.2 B.3 C.4 D.56.下列角度中,不是多边形内角和的只有()A.540°B.720°C.960°D.1080°7.一个多边形的每一个顶点处取一个外角,这些外角中最多有钝角(•)A.1个B.2个C.3个D.4个8.一个多边形除了一个内角外,其余各内角的和为1700°,求多边形的边数.9.一个零件的形状如图中阴影部分.按规定∠A应等于90º,∠B、∠C应分别是29º和21º,检验人员度量得∠BDC=141º,就断定这个零件不合格.你能说明理由吗?10.一个多边形,它的外角最多有几个是钝角?说说你的理由.11.在四边形ABCD中,∠D=60°,∠B比∠A大20°,∠C是∠A的2倍,求∠A,∠B,∠C的大小.12. 一个四边形截去一个角后就一定是三角形吗?画出所有可能的图形,并分别说出内角和和外角和变化情况.。

八年级上册研说教材临朐第四中学贺同明大家好:今天我研说的内容是青岛版八年级数学。
主要从说课标、说教材、说建议三个方面进行说明。
说课标包括课程目标、内容标准。
说教材包括教材编写特点、编排体例、内容结构、知识整合。
说建议包括教学建议、评价建议、课程资源的开发与利用。
说课标一、课程目标根据课标要求,要让学生通过数学学习,获得适应未来社会生活和进一步发展,所必需的重要数学知识以及基本的数学思想方法。
具体目标如下:知识与技能经历将一些实际问题抽象为数与代数问题的过程,掌握数与代数基础知识和基本技能,并能解决简单的问题。
数学思考经历运用数学符号和图形描述现实世界的过程,建立初步的数感和符号感,发展抽象思维。
在探索图形的性质中,初步建立空间观念,发展几何直观。
解决问题初步学会从数学的角度提出问题、理解问题,并能综合运用所学的知识和技能解决问题,发展应用意识。
形成解决问题的一些基本策略。
感情与态度能积极参与数学学习活动。
体验数学活动充满着探索性和创造性;感受证明过程的严谨性以及结论的确定性。
二、内容标准:初中数学按课程标准主要分为数与代数、空间与图形、统计与概率、实践与综合应用四个领域。
数与代数包括数与式、方程与不等式、函数,本册教材数与代数安排学习了1、实数,要了解算数平方根、平方根的意义以及两者的区别与联系,勾股定理及逆定理。
2、乘法公式与因式分解,使学生正确理解乘法公式与因式分解的意义,认识公式的结构特征以及字母的广泛含义。
3、分式与分式方程,了解分式的基本性质,能够进行混合运算;理解连比的概念和比例的基本性质,会解可化为一元一次方程的分式方程,并能解决实际问题,4、一元一次不等式,了解不等式的解与不等式组的解集的意义,知道解法,并能解决实际问题。
空间与图形包括轴对称与轴对称图形,轴对称图形及其性质,线段的垂直平分线及其性质,角平分线及其性质以及等腰三角形的有关知识。
统计与概率主要研究样本与估计。
了解抽查与普查的区别,平均数、中位数、众数的联系与区别,以及平均数与加权平均数的区别与联系。

概率问题及其简单应用(一)【知识梳理】1.了解频数、频率、必然事件和不可能事件、确定事件、随机事件、频率的稳定性等概念,并能进行有效的解答或计算.2.在具体情境中了解概率的意义;能够运用列举法(包括列表、画树状图)求简单事件发生的概率.能够准确区分确定事件与不确定事件.3. 必然事件发生的概率是1,记作P (A )=1不可能事件发生的概率为0,记作 P (A )=0随机事件发生的概率是0和1之间的一个数,即0<P (A )<1【思想方法】概率主要是研究现实生活中和客观世界中的随机现象,它通过对事件发生可能性的刻画,来帮助人们做出合理的决策.随着社会的不断发展 概率的思想方法也越来越重要.因此, 概率知识是各地中考重点考查内容之一.加强统计与概率的联系,这方面的题型以综合题为主,将逐渐成为新课标下中考的热点问题.【例题精讲】 例1.(2008年张家界)下列事件中是必然事件的是( )A.明天我市天气晴朗B.两个负数相乘,结果是正数C.抛一枚硬币,正面朝下D.在同一个圆中,任画两个圆周角,度数相等 例2.在一次抽奖游戏中,主持人说,这次中奖的可能性有10%,就是说100个人中有10个人可以获奖.旁边的一个人就想,我在这儿等着,等前面的90个人抽完,看看他们抽到奖没有,如果他们没有抽到奖,那我就可以抽到奖了.因为中奖的可能性是10%.你说这个人的想法对吗?例3. (2008年湘潭)某中学为促进课堂教学,提高教学质量,对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了“频率分布表”和“频数分布条形图”(如图2).请你根据图表中提供的信息,解答下列问题.频率分布表:(1)补全“(2)在“频数分布条形图”中,将代号为“4”的部分补充完整;(3)你最喜欢以上哪一种教学方式或另外的教学方式,请提出你的建议,并简要说明理由.(字数在20字以内)【当堂检测】1.下列事件你认为是必然事件的是()A.中秋节的晚上总能看到圆圆的月亮; B.明天是晴天C.打开电视机,正在播广告; D.太阳总是从东方升起2.将五张分别画有等边三角形、平行四边形、矩形、等腰梯形、正六边形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张卡片,图形一定是中心对称图形的概率是()A.15B.25C.35D.453.在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是()A.12B.9C.4D.34.在中考体育达标跳绳项目测试中,1min跳160次为达标,•小敏记录了他预测时,1min跳的次数分别为145,155,140,162,164,•则他在该次预测中达标的概率是_________.5.有一道四选一的选择题,某同学完全靠猜测获得结果,则这个同学答对的概率是________.6.在一所4000人的学校随机调查了100人,其中有76人上学之前吃早饭,•在这所学校里随便问一个人,上学之前吃过早餐的概率是________.7. 书架上有数学书3本,英语书2本,语文书5本,从中任意抽取一本是数学书的概率是()A.110B.35C.310D.158.小华与小丽设计了A B,两种游戏:游戏A的规则:用3张数字分别是2,3,4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字.若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.游戏B的规则:用4张数字分别是5,6,8,8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌.若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜;否则小丽获胜.请你帮小丽选择其中一种游戏,使她获胜的可能性较大,并说明理由.。

临朐第四中学2013年中考数学模拟试题一、选择题(每小题3分,共36分)1.已知a 等于( ) A .aB .a -C .1-D .02.若n (0n ≠)是关于x 的方程220x mx n ++=的根,则m +n 的值为 ( )(A )1 (B )2 (C )-1 (D )-23.已知⊙o 是ABC △的外接圆,若AB =AC =5,BC =6,则⊙o 的半径为( ) A .4 B .3.25 C .3.125 D .2.254.在一个不透明的袋子里装有两个红球和两个黄球,它们除颜色外都相同.随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,两次都摸到黄球的概率是( )A .12B .13C .14D .165.一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的直径是( )A .0.4米B .0.5米C .0.8米D .1米6.已知矩形ABCD 的边AB =6,AD =8.如果以点A 为圆心作⊙A ,使B 、C 、D 三点中在圆内和在圆外都至少有一个点,那么⊙A 的半径r 的取值范围是( )A .6<r <10B .8<r <10C .6<r ≤8D .8<r ≤107.小莹准备用纸板制作一顶圆锥形“圣诞帽”,使“圣诞帽”的底面周长为π18cm ,高为40cm .裁剪纸板时,小莹应剪出的扇形的圆心角约为( ) A .72º B .79º C .82º D .85º8.小强从如图所示的二次函数2y ax bx c =++的图象中,观察得出了下面五条信息:(1)0a <;(2)1c >;(3)0b >;(4)0a b c ++>;(5)0a b c -+>.你认为其中正确信息的个数有( ) A .2个 B .3个 C .4个 D .5个9.已知两圆半径分别为2和3,圆心距为d ,若两圆没有公共点,则下列结论正确的是( ) A .01d << B .5d > C .01d <<或5d > D .01d <≤或5d > 10.已知y 关于x 的函数图象如图所示,则当0y <时,自变量x 的取值范围是( ) A .0x < B .11x -<<或2x >C .1x >-D .1x <-或12x <<11.如图,AB 是⊙O 的直径,C ,D 为圆上两点,∠AOC =130°,则∠D 等于( ) A .25° B .30° C .35° D .50°12.二次函数2y ax bx c =++的图象如图所示,则一次函数24y bx b ac =+-与反比例函数ab cy x++=在同一坐标系内的图象大致为( )二、(每小题3分,共15分)13.如图,⊙o 1和⊙o 2的半径为1和3,连接12OO ,交⊙o 2于点P ,128OO =,若将⊙o 1绕点P按顺时针方向旋转360,则⊙o 1和⊙o 2共相切_____次.14.如图,⊙o 的半径5cm OA =,弦8cm AB =,点P 为弦AB 上一动点,则点P 到圆心O 的最短距离是cm .15.如图,AOB ∠是放置在正方形网格中的一个角,则cos AOB ∠的值是 .xxxxx第31题图DBOC第11题图16.如图,ABC △与AEF△中,A B A E B ==∠=∠,,,交EF 于D.给出下列结论: ①AFC C ∠=∠; ②DF CF =;③ADE FDB △∽△; ④BFD CAF ∠=∠.其中正确的结论是 .(填写所有正确结论的序号).17.某楼梯的侧面视图如图所示,其中4AB =米,30BAC ∠=°,90C ∠=°,因某种活动要求铺设红色地毯,则在AB 段楼梯所铺地毯的长度应为 .三、解答题18. (本题满分10分)已知:如图,AB 是⊙O 的切线,切点为A ,OB 交⊙O 于C ,且C 为OB 中点.过C 点的弦CD 使∠ACD= 45°,弧AD 的长为π22,求弦AD 、AC 的长。

青岛版数学统计专题说教材稿尊敬的各位领导、老师们:大家好!很高兴能有这样一个机会跟大家一起交流,接下来请允许我和您一起走进青岛版数学统计与概率专题,我将从课标要求;教材分析;建议分析三方面对本套教材统计与概率专题进行研说。
不当之处,敬请各位老师批评指正,一、课标要求(一)、新课标对本学段统计与概率知识的学习提出了四个方面的专题目标:1、知识与技能:经历在实际问题中收集和处理数据、利用数据分析问题、获取信息的过程,掌握统计与概率的基础知识和基本技能。
2、数学思考:体会统计方法的意义,发展统计观念,感受随机现象。
3、解决问题:初步学会从数学的角度提出问题、理解问题,并能综合运用所学的知识和技能解决问题,发展应用意识。
4、情感与态度:能积极参与数学学习活动,对数学有好奇心与求知欲。
这四方面的目标是一个密切联系的整体,其中数学思考、解决问题、情感与态度的发展离不开知识与技能的学习,同时知识与技能的学习必须以有利于其他目标的实现为前提。
(二)课程标准在本学段的内容标准的具体目标:可概括为:9个“能”,6个“会,”2个“理解”,1个“知道”,2个“了解”,4个“探索、体会”。
2个“了解”是:(1)了解频数分布的意义和作用。
(2)在具体情境中了解概率的意义。
1个“知道”是:通过实验,获得事件发生的频率;知道大量重复实验时频率可作为事件发生概率的估计值。
2个“理解”是:(1)在具体情境中理解加权平均数。
(2)通过实例,理解频数、频率的概念。
9个“能”是:(1)从事收集、整理、描述和分析数据的活动,能用计算器处理较为复杂的统计数据。
(2)通过丰富的实例,感受抽样的必要性,能指出总体、个体、样本。
(3)根据具体问题,能选择合适的统计量表示数据的集中程度。
(4利用频数分布表,频数分布直方图和频数折线图,能解决简单的实际问题。
(5)能用样本的平均数、方差来估计总体的平均数和方差。
(6)根据统计结果作出合理的判断和预测,能比较清晰地表达自己的观点,并进行交流。
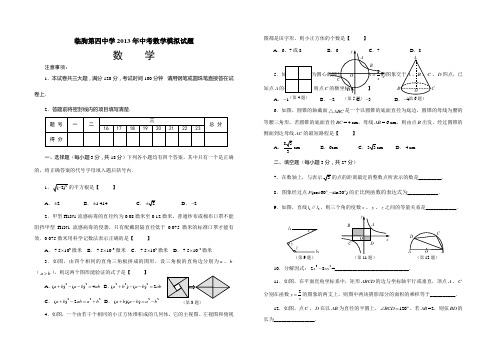
临朐第四中学2013年中考数学模拟试题数 学注意事项:1.本试卷共三大题,满分120分,考试时间100分钟. 请用钢笔或圆珠笔直接答在试卷上.2.答题前将密封线内的项目填写清楚.题 号 一 二 三总 分 16 17 18 19 20 21 22 23 得 分一、选择题(每小题3分,共18分)下列各小题均有四个答案,其中只有一个是正确的,将正确答案的代号字母填入题后括号内.1.2(2)-的平方根是【 】A .2±B . 1.414±C .2±D .2-2.甲型H1N1流感病毒的直径约为0.08微米至0.12微米,普通纱布或棉布口罩不能阻挡甲型H1N1流感病毒的侵袭,只有配戴阻隔直径低于0.075微米的标准口罩才能有效.0.075微米用科学记数法表示正确的是【 】A .37.510⨯微米 B .37.510-⨯微米 C .27.510⨯微米 D .27.510-⨯微米 3.如图,由四个相同的直角三角板拼成的图形,设三角板的直角边分别为a 、b (a b >),则这两个图形能验证的式子是【 】A .22()()4a b a b ab +--= B .222()()2a b a b ab +--=C .222()2a b ab a b +-=+D .22()()a b a b a b +-=-4.如图,一个由若干个相同的小正方体堆积成的几何体,它的主视图、左视图和俯视图都是田字形,则小正方体的个数是【 】A .6、7或8B .6C .7D .85.如图,以原点为圆心的圆与反比例函数3y x =的图象交于A 、B 、C 、D 四点,已知点A 的横坐标为1,则点C 的横坐标【 】A .1-B .2-C .3-D .4-6.如图,圆锥的轴截面ABC △是一个以圆锥的底面直径为底边,圆锥的母线为腰的等腰三角形,若圆锥的底面直径BC = 4 cm ,母线AB = 6 cm ,则由点B 出发,经过圆锥的侧面到达母线AC 的最短路程是【 】A .833cm B .6cm C .33cm D .4cm 二、填空题(每小题3分,共27分)7.在数轴上,与表示3的点的距离最近的整数点所表示的数是_________.8.图象经过点(cos60,sin30)P ︒-︒的正比例函数的表达式为____________.9.如图,直线12l l ∥,则三个角的度数x 、y 、z 之间的等量关系是____________.10.分解因式:3228x xy -=_____________________________.11.如图,在平面直角坐标系中,矩形ABCD 的边与坐标轴平行或垂直,顶点A 、C 分别在函数2y x=的图象的两支上,则图中两块阴影部分的面积的乘积等于__________. 12.如图,点C 、D 在以AB 为直径的半圆上,120BCD ∠=︒,若AB =2,则弦BD 的长为________________.13.某著名篮球运动员在一次比赛中20投16中得28分(罚球命中一次得1分),其中3分球2个,则他投中2分球的频率是__________.(第3题)(第4题) ACxyO (第5题) BD ABCO(第6题) · l 1 x(第9题)l 2zyACxy O(第11题)BDAB CO (第12题)·D14.如图,若开始输入的x 的值为正整数,最后输出的结果为144,则满足条件的x 的值为_____________________.15.如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE 、CF 交于点G ,半径BE 、CD 交于点H ,且点C 是 AB 的中点,若扇形的半径为2,则图中阴影部分的面积等于____________________.三、解答题(本大题共8个小题, 满分75分) 16.(8分)解方程:32322x x x -=+-.17.(9分)国务院办公厅下发《关于限制生产销售使用塑料购物袋的通知》,从2008年6月1日起,在全国范围内禁止生产销售使用超薄塑料袋,并实行塑料袋有偿使用制度,“禁塑令”有效的减少了“白色污染”的来源。
等式的基本性质学习目标:1、通过实例,理解等式的基本性质.2、会用等式的两条性质将等式变形;能对变形说明理由.3、应用等式的性质把简单的一元一次方程化成“x=a”的形式.知识导学:考你一下:1、小明和小营今年是同岁,那5年之后两个人还是同岁吗?2、小明比小营今年大3岁,10年之后小明比小营还大3岁吗?自主导学:自学课本163至164页内容,完成以下问题:一、等式的基本性质11、用语言叙述等式的基本性质1:2、用字母表示等式的基本性质1:3、尝试练习:(1)如果a=b,那么a+5=a+( )(2)如果x-3=5,那么x=5+( )(3)如果2x=x-2,那么x= ( )(4)如果x+3=10,那么x=10-( )(5)由等式a=b,得到a+10=b+10,其理由是______________________________. (6)能否由3x-1=2x得到x=1?二、等式的基本性质21、用语言叙述等式的基本性质2:2、用字母表示等式的基本性质2:3、尝试练习:(1)如果-3x=18,那么x=____;(2)如果a4=2,那么a=____(3)从x=y 能不能得到yx=99呢?为什么?(4)从-3a=-3b 能不能得到a=b 呢?为什么?(5)如果12x=3,那么x= ( ) (6)如果3x=-15,那么x= ( )巩固练习:1、若a=b ,请同学根据等式性质编出三个等式并说出你的编写根据。
2、填空:(1)在等式7m-6=3m 的两边同时 _____________,得到4m=6,这是根据 __________________________.(2)在等式5a-7=8-9a 的两边同时 ____________,得到14a=15, 这是根据 ______________________.(3)在等式43x=-5的两边都______ 或 _________,得到x=-320.(4)a+b=0,可得a=_________;由a-b=0,可得a= _________;由ab=1,可得a=______________.(5)由a=-2,b=-2,可得a ______b ;由a=-b ,可得b= _______,-b=______.(6)比x 的一半少3的数是y 的32,用等式可以表示为______________ . 反馈练习:1.选择题:(1)下列结论正确的是( )A .若x+3=y-7,则x+7=y-11;B .若7y-6=5-2y,则7y+6=17-2y;C .若0.25x=-4,则x=-1;D .若7x=-7x,则7=-7.(2)下列说法错误的是( ).A .若a y a x ,则x=y;B .若x 2=y 2,则-4x 2=-4y 2;C .若-41x=6,则x=-23; D .若6=-x,则x=-6.(3)已知等式ax=ay,下列变形错误的是( ).A .x=yB .ax+1=ay+1C .ay=-axD .3-ax=3-ay(4)下列说法正确的是( )A .等式两边都加上一个数或一个整式,所得结果仍是等式;B .等式两边都乘以一个数,所得结果仍是等式;C .等式两边都除以同一个数,所以结果仍是等式;D .一个等式的左、右两边分别与另一个等式的左、右两边分别相加,所得结果仍是等式;2、把一元一次方程5x-2=x+2变形为x=a 的形式,并说明每步变形的依据。
2013年初中数学学业水平考试模拟试题一. 选择题(本大题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有 一项是符合题目要求的。
)1.在下列运算中,计算正确的是()..3 ? 6 A ・ ci • cr = a B. ―夕=a4 C. (a 2)3 = a 67 7D ・ a"+cr =a 2.下列图形中既是轴对称图形又是中心对称图形的是() 企☆ O3.国家游泳中心一一 “水立方”是北京2008年奥运会场馆之一,它的外层膜的展开面积约 为260 000平方米,将260 000用科学记数法表示应为(). A. 0.26X106 B. 2.6X105 C. 2.6xl064. 在如图所示的四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )A.B.C.D. ffl <®> A D. 26X104 如图所示,若k>0 H b 〈0,则函数y 二kx+b 的大致图彖是() D.A- C • B. 商场经理要了解哪种型号最畅销,则上述数据的统讣量中,対商场经理来说最有意义的是三、解答题(本大题共9小题,共72分.解答应写出文字说明、证明过程或演算步骤)A.平均数 B •中位数 C.众数 D.方差8.对于抛物线y = —l(x — 5)2+3, 下列说法匸确的是(A.开口向下,顶点坐标(5,3)B.开口向上,顶点坐标(5,3)C.开口向下,顶点坐标(-5,3)D.开口向上,顶点坐标(-5,3) 9.如图,在5x5方格纸中,将图①中的三角形甲平移到图②中所示的位置, 与三角形乙拼 成一个矩形,那么,下面的平移方法中,正确的是(A. 先向下平移3格,再向右平移2格B. 先向下平移2格,再向右平移1格C. 先向下平移2格,再向右平移2格D. 先向下平移3格,再向右平移1格10.己知二次函数尸尼+兀的图像如图所示,则在“①&V0,②b>0,③c<0, @b 2-4ac>0"中正确的的个数为().A. 1B. 2C. 3D. 4 二、填空题(本大题共6小题,每小题3分,共18分・)11.因式分解:2m —3n = _________ .12. 一家商店将某种商品按成本价提高50%后,标价为450元,又以8折出售,则售出这件 商品可获利润 __________ 元•13.在一次校园朗诵比赛中,七位评委给小丽打分的成绩如下:8.6, 9.7, & 5, 8.6, 9.6,8.6, 7.2,则这组数据的中位数是 ________________ .14. 如图,点A 、B 、C 是OO 上的三点,ZBAC=50°,则ZOBC 的度数是 ______________15. 一个圆锥的底面圆的直径为6cm,高为4cm,则它的侧而积为 ________ cm 2 (结果保留兀).且与CD 边交于点乂 若個=6,初=4,设OM=x, ON=y,则y 与x 的函数关系式为 __________ o图① 图② (第9题图)A(第16题图)17.(本题满分7分)2兀-1 W2,解不等式组x-1 x 并将其解集表示在数轴上.-------------- V — 94 319.(本题满分9分)小明对本班同学上学的交通方式进行了一次调查,他根据采集的数据, 绘制了下面的统计图1和图2.请你根据图中提供的信息,解答下列问题:(1) 计算本班骑自行车上学的人数,补全图1的统计图;(2) 在图2中,求出“乘公共汽车”部分所对应的圆心角的度数,补全图2的统计图 (要求写出各部分所占的百分比);(3)观察图1和图2,你能得出哪些结论?(只要求写出一条).18.(本题满分6分)化简:2x 1 兀 2_1一R图1 图220.(本题满分8分)如图,在△ ABC中,ZACB = 90\ ZB =30°, CD,分别是AB 边上的中线和高.(1)求证:AE = ED ;(2)若AC = 2f求的周长.21.(本题满分8分)某商场在今年“六•一”儿童节举行了购物摸奖活动.摸奖箱里有四个标号分别为1, 2, 3, 4的质地、大小都相同的小球,任意摸出一个小球,记下小球的标号后,放回箱里并摇匀,再摸出一个小球,又记下小球的标号.商场规定:两次摸出的小球的标号之和为“8”或“6”时才算中奖.请结合“树状图法”或“列表法”,求出顾客小彦参加此次摸奖活动时中奖的概率.22.(本题满分8分)广州市中山大道快速公交(简称BRT)试验线道路改造工程中,某工稈队小分队承担了100米道路的改造任务.为了缩短对站台和车道施工现场实施围蔽的时间,在确保工程质量的前提下,该小分队实际施工时每天比原计划多改造道路10米,结果提前5天完成了任务,求原计划平均每天改造道路多少米?23.(本题满分8分)如图,已知AB是0 0的直径,AC是弦,D为AB延长线上一点,DC = AC f ZACD = \20\ BD = \0.判断DC是否为O O的切线,并说明理由;(第20题图)A(第23题图)24.(本题满分8分)如图:四边形ABCD屮,E、F、G、H分别为各边的屮点,顺次连结E、F、G、H,把四边形EFGI1称为中点四边形。