有限元理论基础

有限元理论基础及应用有限元理论是应用于工程计算领域的一种数值分析方法，它是通过将连续的结构或物体分割成有限数量的离散单元，然后在每个单元上进行近似计算，最终得到整个结构或物体的近似解。

有限元理论广泛应用于结构分析、流体力学、电磁场分析等领域，是工程计算的重要工具。

有限元理论的基础是有限元方法，它将连续的结构或物体以网格的形式划分成一系列有限的单元，通过在每个单元内进行节点位移或其他物理量的近似表示，建立起离散的数学模型。

在有限元方法中，常用的单元形状包括线元、三角形单元、四边形单元等。

每个单元的节点之间通过连接的方式形成整个结构的网格。

有限元理论的基本原理是将连续的物理问题转化为离散的代数问题，通过求解代数方程组得到数值结果。

其基本步骤包括：1.离散化：将连续的结构或物体划分为离散的单元，并在每个单元上建立近似解。

2.建立单元方程：根据结构或物体的本构关系、边界条件等，建立每个单元的方程。

3.组装：根据单元之间的连接方式，将每个单元的方程组装成整个结构或物体的方程。

4.边界条件处理：考虑边界条件对结构或物体的约束作用，修改方程。

5.求解代数方程组：将边界条件处理后的方程组进行求解，得到数值解。

有限元理论的应用非常广泛，主要包括：1.结构分析：有限元方法在结构力学领域的应用非常广泛，可以用于预测结构的应力、变形、疲劳寿命等。

例如，在建筑工程中，可以使用有限元方法对建筑结构进行静力分析，以确保结构的稳定性和安全性。

2.流体力学：有限元方法在流体力学领域的应用包括流体流动、传热、空气动力学等方面。

通过将流体分割成离散的单元，并建立流体的动量方程、能量方程等，可以模拟和预测流体的各种特性。

3.电磁场分析：有限元方法可以用于模拟和分析电磁场的分布、辐射、散射等现象。

在电子器件设计中，有限元方法可以用于预测电磁场的影响和优化设计。

此外，有限元方法还应用于声学、热力学、生物力学等领域。

它的优势包括模拟结果的准确性、适用于复杂几何形状和边界条件、计算速度较快等。

有限元法的理论基础有限元法是一种离散化的数值计算方法，对于结构分析而言，它的理论基础是能量原理。

能量原理表明，在外力作用下，弹性体的变形、应力和外力之间的关系受能量原理的支配，能量原理与微分方程和定解条件是等价的。

下面介绍有限元法中经常使用的虚位移原理和最小势能原理。

1.虚位移原理虚位移原理又称虚功原理，可以叙述如下：如果物体在发生虚位移之前所受的力系是平衡的(物体内部满足平衡微分方程，物体边界上满足力学边界条件），那么在发生虚位移时，外力在虚位移上所做的虚功等于虚应变能（物体内部应力在虚应变上所做的虚功）。

反之，如果物体所受的力系在虚位移（及虚应变）上所做的虚功相等，则它们一定是平衡的。

可以看出，虚位移原理等价于平衡微分方程与力学边界条件。

所以虚位移原理表述了力系平衡的必要而充分的条件。

虚位移原理不仅可以应用于弹性性力学问题，还可以应用于非线性弹性以及弹塑性等非线性问题。

2.最小势能原理最小势能原理可以叙述为：弹性体受到外力作用时，在所有满足位移边界条件和变形协调条件的可以位移中，真实位移使系统的总势能取驻值，且为最小值。

根据最小势能原理，要求弹性体在外力作用下的位移，可以满足几何方程和位移边界条件且使物体总势能取最小值的条件去寻求答案。

最小势能原理仅适用于弹性力学问题。

2.2有限元法求解问题的基本步骤弹性力学中的有限元法是一种数值计算方法，对于不同物理性质和数学模型的问题，有限元法的基本步骤是相同的，只是具体方式推导和运算求解不同，有限元求解问题的基本步骤如下。

2.2.1问题的分类求解问题的第一步就是对它进行识别分析，它包含的更深层次的物理问题是什么？比如是静力学还是动力学，是否包含非线性，是否需要迭代求解，要从分析中得等到什么结果等。

对这些问题的回答会加深对问题的认识与理解，直接影响到以后的建模与求解方法的选取等。

2.2.2建模在进行有限元离散化和数值求解之值，我们为分析问题设计计算模型，这一步包括决定哪种特征是所要讨论的重点问题，以便忽略不必要的细节，并决定采用哪种理论或数学公式描述结果的行为。

有限元分析概念有限元法：把求解区域看作由许多小的在节点处相互连接的单元（子域）所构成，其模型给出基本方程的分片（子域）近似解，由于单元（子域）可以被分割成各种形状和大小不同的尺寸，所以它能很好地适应复杂的几何形状、复杂的材料特性和复杂的边界条件有限元模型：它是真实系统理想化的数学抽象。

由一些简单形状的单元组成，单元之间通过节点连接，并承受一定载荷。

有限元分析：是利用数学近似的方法对真实物理系统（几何和载荷工况）进行模拟。

并利用简单而又相互作用的元素，即单元，就可以用有限数量的未知量去逼近无限未知量的真实系统。

线弹性有限元是以理想弹性体为研究对象的，所考虑的变形建立在小变形假设的基础上。

在这类问题中，材料的应力与应变呈线性关系，满足广义胡克定律；应力与应变也是线性关系，线弹性问题可归结为求解线性方程问题，所以只需要较少的计算时间。

如果采用高效的代数方程组求解方法，也有助于降低有限元分析的时间。

线弹性有限元一般包括线弹性静力学分析与线弹性动力学分析两方面。

非线性问题与线弹性问题的区别：1）非线性问题的方程是非线性的，一般需要迭代求解；2）非线性问题不能采用叠加原理；3）非线性问题不总有一致解，有时甚至没有解。

有限元求解非线性问题可分为以下三类：1）材料非线性问题材料的应力和应变是非线性的，但应力与应变却很微小，此时应变与位移呈线性关系，这类问题属于材料的非线性问题。

由于从理论上还不能提供能普遍接受的本构关系，所以，一般材料的应力与应变之间的非线性关系要基于试验数据，有时非线性材料特性可用数学模型进行模拟，尽管这些模型总有他们的局限性。

在工程实际中较为重要的材料非线性问题有：非线性弹性（包括分段线弹性）、弹塑性、粘塑性及蠕变等。

2）几何非线性问题几何非线性问题是由于位移之间存在非线性关系引起的。

当物体的位移较大时，应变与位移的关系是非线性关系。

研究这类问题一般都是假定材料的应力和应变呈线性关系。

它包括大位移大应变及大位移小应变问题。

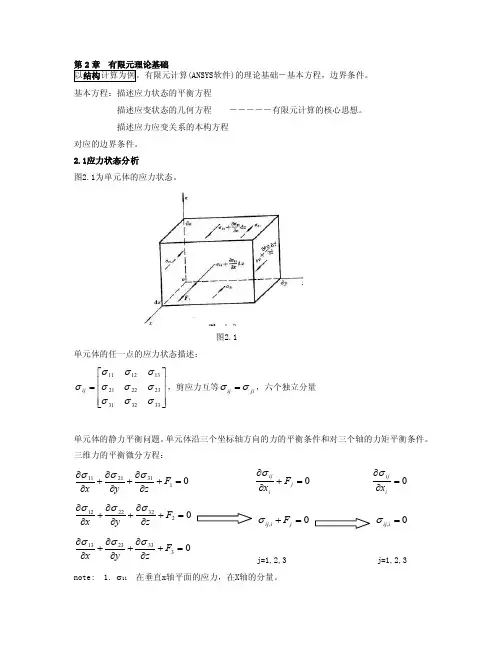
(ANSYS 软件)的理论基础－基本方程，边界条件。

基本方程：描述应力状态的平衡方程描述应变状态的几何方程 －－－－－有限元计算的核心思想。

描述应力应变关系的本构方程 对应的边界条件。

2.1应力状态分析图2.1为单元体的应力状态。

图2.1 单元体的任一点的应力状态描述：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211σσσσσσσσσσij ，剪应力互等ji ij σσ=，六个独立分量单元体的静力平衡问题。

单元体沿三个坐标轴方向的力的平衡条件和对三个轴的力矩平衡条件。

三维力的平衡微分方程：1312111=+∂∂+∂∂+∂∂F z y x σσσ 0=+∂∂j i ij F x σ 0=∂∂i ij x σ2322212=+∂∂+∂∂+∂∂F z y x σσσ0,=+j i ij F σ0,=i ij σ 03332313=+∂∂+∂∂+∂∂F z y x σσσ j=1,2,3 j=1,2,3note: 1. σ11 在垂直x 轴平面的应力，在X 轴的分量。

2. F 为体力，包括：重力、磁力、惯性力，与物体的质量成正比。

F i 为I 轴的体力分量。

3.物体表面单位面积的面力T 三个分量为T x ,T y ,T z ,或T １,T ２,T ３,应力σ的三个分量σx ,σy ,σz 或σ1,σ2,σ3 应力边界条件：332313232221223121111σσσσσσσσσ++=++=++=T T T 3,2,1===i T T iji ji i σσ表达作用在物体表面单位面积丧的面力T 与物体内的应力分量之间的关系。

2.2 应变状态分析 图2.2为单元体的应变状态。

图2.2单元体的一点的应变状态的张量描述：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211εεεεεεεεεεεεεεεεεεεzz zy zx yz yy yxxz xy xxij 与应力状态相似。

通俗易懂的有限元基础原理
有限元分析是一种数值计算方法，用于解决结构力学和其他工程领域的问题。

以下是通俗易懂的有限元基础原理解释：
1. 分割结构：有限元分析中的第一步是将要分析的结构分割成许多小的、简单的部分，称为有限元。

类似于拼图，每个有限元代表结构中的一小部分。

2. 建立本构关系：针对每个有限元，需要建立材料的本构关系，即材料的应力-应变关系。

这是通过材料力学性质的实验测试或理论公式来确定的。

3. 建立单元方程：对于每个有限元，根据其几何形状和材料本构关系建立方程。

这些方程描述了有限元内部的应力和变形之间的关系。

4. 组装全局方程：将所有有限元的方程组装在一起，形成整个结构的全局方程。

这些方程联结了各个有限元之间的边界条件和相互作用。

5. 求解方程：通过数值解法，例如迭代方法或直接求解方法，求解全局方程。

这个过程会得到结构的应力、应变分布以及其他感兴趣的结果。

6. 分析结果：最后，分析人员可以根据求解结果，评估结构的性能，例如应力、变形、位移、振动或热分布等。

这些结果可以帮助工程师优化结构设计、评估结构安全性、指导修复或改进结构性能。

总体来说，有限元分析将大型、复杂的结构问题简化为许多小的、简单的部分，通过数值方法求解其力学行为。

这种方法广泛应用于工程领域，以实现更准确、高效的结构设计和分析。

有限元基础理论考试复习资料1.有限元分析的步骤是怎样的？答：（1）力学模型的确定，建立积分方程。

（2）将结构进行离散化，包括单元划分、结点编号、单元编号、结点坐标计算、位移约束条件确定。

（3）单元函数确定，等效结点力的计算。

（4）单元分析，刚度矩阵的计算，先逐个计算单元刚度，再组装成整体刚度矩阵。

（5）总体分析，建立整体平衡方程，引入约束条件，求解结点位移。

（6）由结点位移计算单元应变及应力。

2.有限元（FEM）离散化体现在哪几个方面？答：1.物体本身离散化2.边界条件离散化3.载荷离散化3.有限单元法的基本思想是什么？答：有限单元法的基本思想是将物体（即连续的求解域）离散成有限个且按一定方式相互联结在一起的单元的组合，来模拟或逼近原来的物体，从而将一个连续的无限自由度问题简化为离散的有限自由度问题求解的一种数值分析法。

4.什么是单元离散化？答：离散化既是将连续体用假想的线或面分割成有限个部分，各部分之间用有限个点相连。

每个部分称为一个单元，连接点称为结点。

5.连续体结构分析有哪几种基本假定？答：（1）连续性假设；（2）完全弹性假设；（3）均匀性假设；（4）各向同性假设；（5）小变形假设。

6.形函数是什么？有什么性质？答：反映单元内位移分布状态，称为位移的形态函数，简称形函数。

其有如下性质：1）形函数在各单元节点上的值，具有“本点是1、他点我零”的性质。

2）在单元内任意一点上，三个形函数之和等于1。

3）三角形单元任意一条边上的形函数，仅与该边的两端点坐标有关。

7.什么是单元，节点，节点力，节点位移，节点载荷，体力，载荷，面力，集中力，位移，应力，应变？答：单元：即原始结构离散后，满足一定几何特性和物理特性的最小结构域。

节点：定义于单元上的特殊点，或单元之间的联系点。

节点力：单元与单元间通过节点的相互作用力。

节点位移：在节点处度量的结构位移。

节点载荷：作用于节点上的外载（等效）。

体力：分布于整个弹性体体积内的外力。