正比例函数与反比例函数的关系

物理中的正比例反比例函数关系正比例函数和反比例函数是物理学中非常重要的概念，被广泛应用于各种物理学问题中。

正比例函数指的是两个变量之间存在着线性关系，而反比例函数则指的是两个变量之间存在着倒数的关系。

在物理学中，这些函数关系经常出现在各种实验测试和数据记录中，因此了解和理解这些函数关系是非常重要的。

一、正比例函数的定义正比例函数是指，存在两个变量之间的线性关系，即当一个变量的值增加时，另一个变量也随之增加，且两个变量在图表上形成一条直线。

具体地说，一个变量的值随着另一个变量的值增加而增加，且增加的幅度与另一个变量的值成比例。

当我们测量一个运动物体的速度时，如果我们将时间和速度作为两个变量绘制成图表，我们会发现，当时间增加时，速度也随之增加，并形成一条经过原点的直线。

这种关系就是正比例函数关系，表达式为：v = k*t，其中v表示速度，t表示时间，k是速度和时间的比例系数。

三、正比例函数和反比例函数的应用正比例函数和反比例函数在物理学中有广泛的应用，下面分别介绍一些常见的应用：（1）正比例函数的应用在机械学中，正比例函数关系最广泛地应用于速度和加速度之间的关系。

当一个物体的速度越快，它的加速度也会越大，它受到的阻力也会越大。

而这种关系可以用正比例函数来表示，表达式为：a = k*v，其中a表示加速度，v表示速度，k是加速度和速度的比例系数。

在空气中飞行的飞机所受到的空气阻力就是一个正比例函数关系。

电阻与电流的关系也可以用正比例函数来表示。

当电路中的电流增加时，电阻也会随之增加，这是因为电流的增加会导致电路中的热量增加，而热量又会引起电阻的增加。

这种关系可以用欧姆定律来表示，即R = V/I，其中R表示电阻，V表示电压，I表示电流。

压力和体积之间的关系也可以用反比例函数来表示。

根据波义尔定理，当温度不变时，气体的体积和压力呈反比例关系，即P1V1 = P2V2，其中P1和V1表示气体压力和体积的初始值，P2和V2表示气体压力和体积的末值。

作业讲评回顾复习教学过程知识点一正比例（1）成正比例的量两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量，他们的关系叫做正比例关系。

用字母表示y/x=k(一定）例如，总价随着数量的变化而变化，总价和数量的比的比值（单价）是一定的，我们就说，总价和数量是成正比例的量。

（2）正比例关系的图象是一条过原点的直线。

练习例1 ：购买面粉的重量和钱数如下表，根据表填空。

（1）( )和( )是两种相关联的量，（）随着（）的变化而变化。

（2）与总价7.6元相对应的重量是（）千克；与6千克相对应的总价是（）元。

（3）总价与重量中相对应的两个数的比值所表示的意义是（）。

（4）因为比值一定，所以表中总价和重量叫做成（）的量。

例2：（4）小英和妈妈的年龄变化情况如下，把表填写完整。

母女的年龄成正比例吗？为什么？例3 某造纸厂每小时造纸1.5吨，2小时、3小时┈┈各造纸多少吨？（1）把下表填写完整。

（2）根据表中的数据，在下图中描出造纸时间和造纸吨数对应的点，再把它们连起来。

知识点二反比例（1）成反比例的量两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，他们的关系叫做反比例关系。

用字母表示x×y=k(一定)例如，长×宽＝面积（一定）长和宽是成反比例的量例1、制造一批零件的个数一定，制造一个零件的时间和需要的总时间成( )比例。

A．成正比例B．成反比例C．不成比例知识点三正比例和反比例有什么相同点和不同点？（1）相同点：正、反比例都是研究两种相关联的量之间的关系，即一种量变化，另一种量也随着变化。

（2）不同点：正比例是两种相关联的量中相对应的两个数的比值（商）一定；反比例是两种相关联的量中相对应的两个数的积一定。

知识点四：正比例和反比例的判断（1）先判断两种量x和y是不是相关联的量，即一种量变化，另一种量也随着变化。

反比例函数与正比例函数的关系反比例函数与正比例函数是数学中常见的函数关系。

它们描述了两个变量之间的关系，其中一个变量的变化与另一个变量的变化成反比例或正比例关系。

反比例函数是指两个变量之间的关系满足一个变量的变化与另一个变量的变化成反比例关系。

具体而言，当一个变量的值增大时，另一个变量的值相应地减小；反之亦然。

反比例函数可以用以下形式来表示：y = k/x，其中k是一个常数，x和y分别表示两个变量的值。

正比例函数是指两个变量之间的关系满足一个变量的变化与另一个变量的变化成正比例关系。

具体而言，当一个变量的值增大时，另一个变量的值也相应地增大；反之亦然。

正比例函数可以用以下形式来表示：y = kx，其中k是一个常数，x和y分别表示两个变量的值。

反比例函数和正比例函数在数学上有很多应用。

下面将分别介绍它们的特点及应用。

反比例函数的特点是当一个变量的值增大时，另一个变量的值相应地减小。

这意味着两个变量之间存在一个倒数关系。

例如，在物理学中，牛顿第二定律描述了物体的加速度与施加在物体上的力成反比例关系。

根据牛顿第二定律，物体的加速度等于施加在物体上的力除以物体的质量。

因此，当施加在物体上的力增大时，物体的加速度减小；反之亦然。

这个关系可以用反比例函数来表示。

正比例函数的特点是一个变量的值的增大与另一个变量的值的增大成正比。

这意味着两个变量之间存在一个比例关系。

例如，在经济学中，供给与需求之间的关系可以用正比例函数来描述。

根据供需理论，当市场上某种商品的需求增加时，供给也会增加；反之亦然。

这个关系可以用正比例函数来表示。

反比例函数和正比例函数在实际问题中有广泛的应用。

它们可以用来描述物理、经济、生物等各个领域中的变量关系。

例如，在物理学中，反比例函数可以用来描述电阻与电流之间的关系，即欧姆定律。

根据欧姆定律，电流等于电压除以电阻。

因此，当电阻增大时，电流减小；反之亦然。

在经济学中，正比例函数可以用来描述生产成本与产量之间的关系。

正比例反比例讲解
正比例和反比例是数学中常见的两个概念,它们描述了两个变量之间的关系。

理解这两个概念对于解决实际问题非常重要。

正比例:
当两个变量的值随着彼此的变化而同步增加或减少时,我们说它们成正比例关系。

换句话说,如果一个变量增加或减少了一定数量,另一个变量也会按相同的比例增加或减少,那么这两个变量就成正比例。

例如:
- 如果一个人的工资与工作时间成正比例,那么工作时间增加10%,工资也会增加10%。

- 如果一辆汽车的行驶距离与油箱中汽油量成正比例,那么油箱中汽油量增加20%,行驶距离也会增加20%。

数学上,如果y = kx,其中k是一个非零常数,那么y与x成正比例关系。

反比例:
当一个变量的值增加时,另一个变量的值减少,反之亦然,我们说它们成反比例关系。

也就是说,如果一个变量增加了一定数量,另一个变量会按相同的比例减少,那么这两个变量就成反比例关系。

例如:
- 如果一个人完成一项工作所需的时间与工人数量成反比例,那么工人数量增加25%,完成工作所需时间会减少25%。

- 如果一个圆的面积与半径的平方成反比例,那么半径增加10%,面积会减少19%(因为面积与半径的平方成反比)。

数学上,如果y = k/x,其中k是一个非零常数,那么y与x成反比例关系。

理解正比例和反比例关系对于解决许多实际问题非常有帮助,如计算工资、距离、面积等。

掌握这些概念有助于我们更好地分析和解决现实生活中的问题。

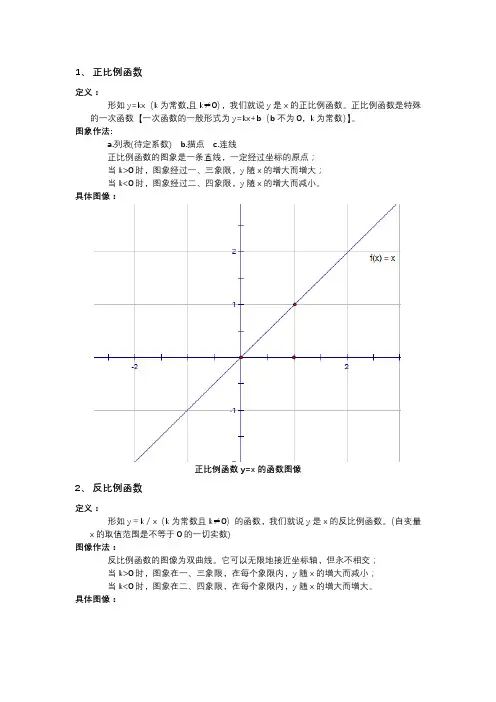
1、正比例函数
定义：
形如y=kx（k为常数,且k≠0），我们就说y是x的正比例函数。

正比例函数是特殊的一次函数【一次函数的一般形式为y=kx+b（b不为0，k为常数）】。

图象作法:
a.列表(待定系数)
b.描点
c.连线
正比例函数的图象是一条直线，一定经过坐标的原点；
当k>0时，图象经过一、三象限，y随x的增大而增大；
当k<0时，图象经过二、四象限，y随x的增大而减小。

具体图像：
正比例函数y=x的函数图像
2、反比例函数
定义：
形如y＝k／x（k为常数且k≠0）的函数，我们就说y是x的反比例函数。

（自变量x的取值范围是不等于0的一切实数)
图像作法：
反比例函数的图像为双曲线。

它可以无限地接近坐标轴，但永不相交；
当k>0时，图象在一、三象限，在每个象限内，y随x的增大而减小；
当k<0时，图象在二、四象限，在每个象限内，y随x的增大而增大。

具体图像：
反比例函数y=1/x的函数图像。

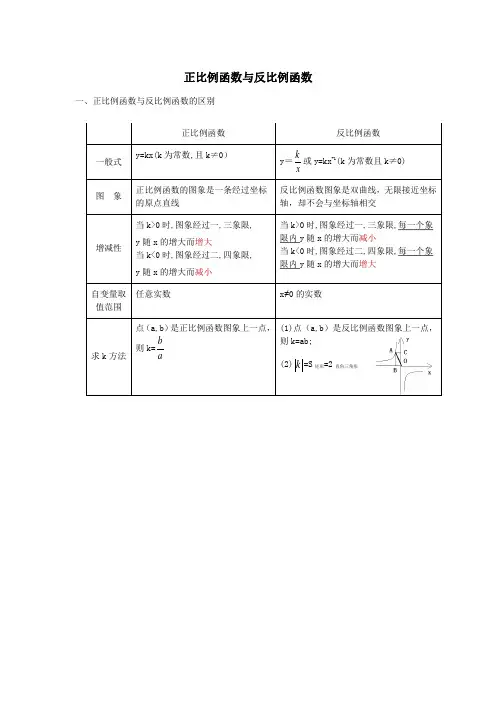
正比例函数与反比例函数一、正比例函数与反比例函数的区别
Q
二、正比例函数与反比例函数的关系
正比例函数与反比例函数图象交于A、B两点，则A、B关于原点对称：（1）OA=OB
（2）AB两点的坐标互为相反数。

即A(a,b),则B(-a,-b)
三、典型例题
例1
如图，正比例函数y=mx与反比例函数
（m、n是非零常数）的图像交于A、B两
点，若点A的坐标为（1，2），则点B的
坐标是（）。

由上二（2）得B的坐标是（-1，-2 ）
例2 已知：反比例函数图像上一点M（-1，3
①求出这个函数的解析式
②求直线MO的解析式
③作MN⊥x轴于N，求
MON
S
④求图中Q的坐标
解：①点M（-1，3）在反比例函数图像上
∴k=xy=-1×3=-3
∴y=-
x
3
比例函数图像上
③作MN⊥x轴于N，则
MON
S
=
2
k
=
2
3
④图中Q与点M关于原点对称，∴Q的坐标为（1，-3）
函数？(2)是反比例函数？并画出它们的图象．
解：(1)由正比例函数定义得
∴m＝1．此时函数解析式变为y＝3x．(2)由反比例函数定义得。

第17课 正比例函数与反比例函数一、 本课主要知识点：1. 正比例函数的解析式是y = kx ( k ≠ 0 )，其图象是一条直线，且必过O （0，0）和 A （1，k ）两点。

练习：若y 与x 成正比例，且x = 5时，y = 12，则y 与x 的函数解析式为 。

2. 直线y = kx ( k ≠ 0 )，当 k > 0时，图象经过第一、三象限，y 随x 的增大而增大；当 k < 0时，图象经过第二、四象限，y 随x 的增大而减小。

练习：(2006年福建省泉州市) 函数x y 4=的图象经过原点、第一象限与第 象限。

3. 反比例函数的解析式是y =xk( k ≠ 0 )，其图象是双曲线。

练习：(1) (2006年安徽省)如果反比例函数y =xk的图象经过点（1，– 2），那么k 的值是( )A ．-21B ．21C ．-2D ．2(2) (2006广东省广州市)若反比例函数ky x=的图象经过点( 1，–1 )，则k 的值是 ．4. 双曲线y =xk( k ≠ 0 )，当 k > 0时，图象经过第一、三象限，在每个象限内y 随x 的增大而减小；当k < 0时，图象经过第二、四象限，在每个象限内y 随x 的增大而增大。

练习：(2006年甘肃省酒泉市)反比例函数2y x=的图象位于第 象限．二、 基础达标训练：（A 组）1. (2006年吉林省课改实验区)下列各点中，在反比例函数6y x=图象上的是（ ）A ．( –2，3 )B ．( 2，–3 )C ．( 1，6 )D ．( –1，6 )2. (2006年福建省南平市) 反比例函数xk y =的图像经过点（2，3-），则=k ．3. (2006年福建省福州市)如图是反比例函数ky x=图象的一支，则k 的取值范围是( )A ．k >1B ． k < 1C ．k > 0D ．k < 04. (2006年辽宁省锦州市)若反比例函数xk y =的图象经过点( -2，3 )，则这个反比例函数的表达式为__ __.5. (2006的江苏省常州市) 已知反比例函数()0≠=k xk y 的图像经过点( 1，– 2 )，则这个函数的表达式是 。

正比例函数和反比例函数的区别（附图）
一：正比例函数
y=kx(k为常数,且k≠0），我们就说y是x的正比例函数，
正比例函数是特殊的一次函数，一次函数的一般形式为y=kx+b（b不为0，k为常数）。

正比例函数的图象是一条直线，一定经过坐标的原点，
当k>0时，图象经过一、三象限，y随x的增大而增大，
当k<0时，图象经过二、四象限，y随x的增大而减小。

二、反比例函数
y＝k／x(k为常数且k≠0) 的函数，我们就说y是x的反比例函数 (自变量x的取值范围是不等于0的一切实数) 。

反比例函数的图像为双曲线，它可以无限地接近坐标轴,但永不相交，
当k>0时，图象在一、三象限,在每个象限内，y随x的增大而减小，
当k<0时，图象在二、四象限,在每个象限内，y随x的增大而增大。

初中数学反比例函数和正比例函数的区别是什么反比例函数和正比例函数是两种不同的函数关系，它们之间有以下几个主要区别：1. 定义：-正比例函数：正比例函数是指两个变量之间的关系，其中一个变量的值是另一个变量的倍数，即两个变量之间存在一个恒定的比例关系。

正比例函数可以表示为y = kx，其中k 是常数，称为比例常数。

-反比例函数：反比例函数是指两个变量之间的关系，其中一个变量的值与另一个变量的倒数成比例，即两个变量之间存在一个恒定的反比例关系。

反比例函数可以表示为y = k/x，其中k 是常数，称为比例常数。

2. 图像：-正比例函数：正比例函数的图像是一条通过原点的直线。

它的斜率表示了比例常数的值，斜率越大，表示比例关系越大。

-反比例函数：反比例函数的图像是一条经过第一象限的双曲线。

它在x 轴和y 轴上都有渐近线，且图像随着x 值的增大而趋于零，随着x 值的减小而趋于无穷大。

3. 变化趋势：-正比例函数：正比例函数中，两个变量的值同时增加或减少。

如果一个变量的值增加，则另一个变量的值也会按照相同的比例增加；反之亦然。

-反比例函数：反比例函数中，当一个变量的值增加时，另一个变量的值会按照相同的比例减少；反之亦然。

其中一个变量的值越大，另一个变量的值越小。

4. 关系特点：-正比例函数：正比例函数表示了两个变量之间的直接关系。

例如，当一辆汽车的速度增加时，它所行驶的距离也会增加。

-反比例函数：反比例函数表示了两个变量之间的间接关系。

例如，当一条水管的截面积增大时，水流通过的速度会减小。

5. 零点和定义域：-正比例函数：正比例函数一般通过原点，因此其零点位于原点，而且定义域为整个实数集。

-反比例函数：反比例函数在定义时，除数不能为零，因此其定义域为除了零的所有实数。

反比例函数和正比例函数的区别在于其定义、图像、变化趋势、关系特点以及零点和定义域。

理解这些区别可以帮助我们更好地应用和解释这两种函数关系在实际问题中的意义。

反比例函数与正比例函数的区别与联系反比例函数与正比例函数是数学中常见的函数形式。

它们在现实生活中也有广泛的应用，如商业、工程、社会等各个领域。

本文将详细讨论反比例函数与正比例函数的区别与联系。

一、反比例函数的定义与特点反比例函数是指一个函数，其值与自变量的倒数成反比例关系，即y=k/x（k为常数）。

其中，x不等于0，y也不等于0。

反比例函数的定义域为x不等于0，值域为y不等于0。

反比例函数的图像呈现出一种双曲线的形态，有两个分支。

与反比例函数相关的一些特点是：1. 零点：反比例函数没有零点，因为它的定义域中没有0。

2. 渐近线：反比例函数有两条渐近线，分别是x=0和y=0。

3. 不对称性：反比例函数充满不对称性，因为当自变量增大时，因变量会减少，反之亦然。

二、正比例函数的定义与特点正比例函数是指一个函数，其值与自变量成正比例关系，即y=kx （k为常数）。

其中，x和y均不能为0。

正比例函数的定义域和值域都为全体实数。

正比例函数的图像呈现出一种直线的形态。

与正比例函数相关的一些特点是：1. 零点：正比例函数的零点为0，因为当x等于0时，y也等于0。

2. 斜率：正比例函数的斜率为常数k，斜率越大，则函数图像越陡峭。

3. 对称性：正比例函数呈现出一种对称性，因为当自变量增大时，因变量也会增大，反之亦然。

三、反比例函数与正比例函数的区别1. 定义与形式反比例函数和正比例函数的定义和形式非常不同。

反比例函数的值与自变量的倒数成反比例关系，而正比例函数的值与自变量成正比例关系。

2. 零点与极点反比例函数没有零点，因为它的定义域不包括0。

而正比例函数的零点为0，因为当自变量等于0时，函数的取值也为0。

而反比例函数有两个极点，一个是x=0，另一个是y=0。

极点是指函数的值越来越接近无穷，当x或y趋近于0时。

3. 图像形态和性质反比例函数的图像呈现双曲线的形态，而正比例函数的图像呈现直线的形态。

正比例函数具有对称性，反比例函数则不具备。

正比例函数与反比例函数正比例函数和反比例函数综合解说客观世界是不断运动和变化着的，在这些变化着的事物中，存在各种各样的变量。

在同一变化过程中，一些变量之间相互依存，一个变量的变化会引起其他变量的相应变化。

函数是体现运动变化的基本数学概念，它从数量角度刻画事物变化的过程，表达变量之间确定的依赖关系。

本章引入了函数的概念，重点讨论正比例函数和反比例函数，并借助与图像的直观，得到它们的一些基本性质，进而应用这些概念和性质，解决一些简单的实际问题。

1正比例函数【知识结构框图表】【本节解读】人们在认识和描述某一事物时，经常会用“量”来具体表达事物的某些特征，量是用“数”来表明大小的。

数与度量单位结合在一起，就是数量。

反比例函数正比例函数定义域和值域函数解析式函数经常涉及的量有长度、面积、体积、质量、温度、时间、速度等。

【基础知识与要点拨】1.变量和常量在变化过程中，可以去不同数值的量叫做变量，保持数值不变的量叫做常量。

比如：圆的周长C与直径D的关系为C＝πD。

C、D是变量，π是常量。

2.函数和自变量在某个变化过程中有两个变量，设为x和y，如果在变量x的允许范围内，变量y随着x的变化而变化，它们之间存在确定的依赖关系，那么变量y叫做变量x的函数，x叫做自变量。

“y是x的函数”用记号y＝f(x)表示，括号内的字母表示自变量，括号外的字母f表示y随着x的变化而变化的规律。

f(a)表示当x＝a时的函数值。

3.定义域和值域函数的自变量允许取值的范围，叫做这个函数的定义域。

对应于自变量的函数值的取值范围，叫做值域。

4.正比例如果两个变量的每一组对应值的比值是一个不等于零的常数，那么就说这两个变量成正比例。

用数学式子表示两个变量x、y成正比例，就是y k=或者y kx=，其中，k是不为零的常数。

x5.正比例函数定义域是一切实数的函数y k x=（k是不为零的常数）叫做正比例函数。

其中常数k叫做比例系数。

确定了比例系数，就可以确定一个正比例函数。

第21课 正比例函数和反比例函数二、【考点整合举例】正比例函数的概念．用待定系数法求函数解析式的方法．如果正比例函数的图像经过点（2，4），那么这个函数的解析式为 ．如图1，正比例函数图像经过点A ，该函数解析式是 ． 1、如果正比例函数的图像经过点（－2，5），那么这个函数的解析式为 ．2、如果反比例函数的图像经过点（2，4），那么这个函数的解析式为 ．反比例函数)0(>=k xky 的性质及数形结合的能力 在直角坐标系内，从反比例函数)0(>=k xky 的图像上的一点分别作x,y 轴的垂线段，与x 、y 轴所围成的矩形的面积是12，那么该函数解析式是 .1、已知y 与x-1成正比例，且图像经过（2，-3）求y 与x 之间的函数解析式 ___。

2、下列函数中，y 随着x 的增大而减少的是 （ ）（A ） x y 4= （B ）x y 4-= （C ）xy 4=（D ）x y 4-=反比例函数图像的性质及从图上获取信息的能力。

（多选题）在函数y=xk（k>0）的图像上有三点),(111y x A 、),(222y x A 、),(333y x A ，已知3210x x x <<<，则下列各式中，正确的是（ ）（A ）310y y << （B ）130y y << （C ）312y y y << （D ）213y y y <<图1（多选题）若点（－1，y 1），（－2，y 2），（2，y 3）在反比例函数y=－x1的图像上，则下列结论中错误的是 （ ）（A ）321y y y >> （B ）312y y y >> （C ） 213y y y >> （D ）123y y y >> 例1．反比例函数y ＝xk 的图像经过点P （m ，n ），其中m 、n 是一元二次方程x 2＋kx ＋4＝0的两个根，求点P 的坐标．例2. 如图，正比例函数y ＝kx （k ＞0）与反比例函数y ＝x1的图像相交于A 、B 两点，过A 作x 轴的垂线交x 轴于点C ，连结BC ，设△ABC 的面积为S ，求S .(1) 反比例函数x2y =，当x=－2时，y 的值为 （ ） （A ）-2 （B ）-1 （C ）1 （D ）2 (2) 如图，A 、C 是函数y ＝x1的图像上的任意两点，过A 作x 轴的垂线，垂足为B ，过C 作y 轴的垂线，垂足为D ，设Rt △AOB 的面积为S 1，Rt △COD 的面积为S 2，则 （ ）（A ）S 1＞S 2 （B ）S 1＜S 2（C ）S 1＝S 2（D ）S 1和S 2的大小关系不能确定(3) 在同一直角坐标系中，函数y =3x 与y =－x1的图像大致是 （ ）（A ）（B ）（C ）（D ）(4) 已知正比例函数y ＝（2m －1）x 的图像上两点A （x 1，y 1），B （x 2，y 2），当x 1＜x 2时，有y 1＞y 2，那么m 的取值范围是 （ ） （A ）m ＜21（B ）m ＞21 （C ）m ＜2 （D ）m ＞02、填充题：(1) 已知y 与x ＋1成正比例，当x ＝5时，y ＝12，则y 关于x 的函数解析式是________． (2) 一个反比例函数在第二象限的图像如图所示，点A 是图像上任意一点，AM ⊥x 轴，垂足为M ，O 是原点，如果△AOM 的面积为3，那么这个反比例函数的解析式是y ＝___________． (3) 已知反比例函数y ＝（m －1）23m x -的图像在第二、四象限，则m 的值为_________．(4) 点A （a ，b ）、B （a －1，c ）均在函数y ＝x1的图像上若a ＜0，则b ____c （填“＞”或“＜”或“＝”）．1、选择题：（1）已知反比例函数y ＝xm21-的图像上两点A （x 1，y 1）、B （x 2，y 2），当x 1＜0＜x 2时，有y 1＜y 2，则m 的取值范围是 （ ） （A ）m ＜0（B ）m ＞0（C ）m ＜21 （D ）m ＞21 （2）若点（3，4）是反比例函数y ＝kx图像上一点，则此函数图像必经过点 （ ） （A ）（2，6）（B ）（2，－6） （C ）（4，－3） （D ）（3，－4）（3）在同一直角坐标系中，正比例函数y =x 与反比例函数y =－x1的图像大致是 （ ）（A ） （B ） （C ） （D ）2、填充题：(1) 已知函数y ＝kx 的图像经过（2，－6），则函数y ＝xk的解析式可确定为____________． (2) 点A （1，m ）在函数y =2x 的图像上，则点A 关于y 轴的对称的点的坐标是______________． (3) 设有反比例函数y ＝xk 1，（x 1，y 1）、（x 2，y 2）为其图像上的两点，若x 1＜0＜x 2时，y 1＞y 2，则k 的取值范围是________．3、解答题：(1) 正比例函数y=kx 的图像与反正比例函数y=x 21的图像交于A （21，m ），正比例函数y=kx 的图像与反比例函数y=x'k 的图像相交于点B （n,4），求k 和k ’． (2) 已知正比例函数y =kx 与反比例函数y =x3的图像都过A （m ，1）点．求：①正比例函数的解析式；②正比例函数与反比例函数的另一个交点的坐标． (3) 已知正比例函数y ＝4x ，反比例函数y ＝xk ． ①求：k 为何值时，这两个函数的图像有两个交点？k 为何值时，这两个函数的图像没有交点？②这两个函数的图像能否只有一个交点？若有，求出这个交点坐标；若没有，请说明理由．考点一：y ＝2x ；y ＝3x .变式演练：1.y ＝5x 2－；2.y ＝8x.考点二：y ＝12x.变式演练：1.y=-3x+3；2.B.考点三：A 、C . 变式演练：B 、C 、D.（二）综合例题：例1：P 点的坐标为（－2，－2） 例2： S △ABC ＝S △AOC ＋S △BOC ＝1．【双基热身反馈】 1. 选择题：（1） B ；（2）C ；（3）D ；（4）A2、填充题：（1）y ＝2x ＋2；（2）y ＝6x.；（3）－2；（4）＜【复习巩固自测】 1、选择题：（1）C ；（2）A ；（3）D2、填充题：（1）y ＝3x－.；（2）（－1，2）；（3）k ＜－13、解答题：（1）解：∵A(21,m)在y=x 21图像上，∴得m=1， A(21,1)．∵A 又在y=kx 图像上，∴得k=2．∵B （n ，4）在y=2x 图像上，∴4=2·n ，n=2，∴B(2,4)．而B 点又是y=x'k 的图像上，∴4=2'k ，k ’=8．（2）①y ＝1x 3；.②（－3，－1）（3）①解：把y ＝4x 代入y ＝x k ，得 4x 2－k ＝0, ∴ x 2＝4k ；由已知，k ≠0，且（ⅰ）当k ＞0时，有x ＝2k 或x ＝－2k； 所以，两函数图像有两个交点（2k ，2k ）和（2k，－2k ）； （ⅱ）当k ＜0时，4k＜0，x 的值不存在，所以两函数图像没有交点； ②若两个图像只有一个交点，只需方程x 2＝4k 有唯一解，即仅当k ＝0时两个图像只有一个交点．但由已知函数y ＝xk可知，应有k ≠0，所以两个图像只有一个交点是不可能存在的．。

正比例反比例的相同点和不同点
正比例和反比例是初中数学中常见的概念。

虽然它们是截然不同的两种关系，但它们也有一些相同点和不同点。

相同点：
1. 都是一种函数关系。

正比例和反比例都可以写成函数形式，其中正比例函数是y=kx，反比例函数是y=k/x，其中k是常数。

2. 都可以用比例式表示。

正比例和反比例都可以用比例式表示，其中正比例式是y/x=k，反比例式是yx=k。

3. 都可以画出直线图像。

正比例和反比例的函数图像都是直线，其中正比例函数的图像是一条通过原点的直线，而反比例函数的图像是一条不通过原点的直线。

不同点：
1. 关系不同。

正比例是两个变量之间的直接关系，即随着一个变量的增加，另一个变量也随之增加；而反比例是两个变量之间的间接关系，即随着一个变量的增加，另一个变量反而会减小。

2. 函数形式不同。

正比例和反比例的函数形式不同，其中正比例是y=kx，反比例是y=k/x，其中k是常数。

3. 比例式不同。

正比例和反比例的比例式也不同，其中正比例式是
y/x=k，反比例式是yx=k。

4. 直线图像不同。

正比例和反比例的直线图像也不同，其中正比例函数的图像是一条通过原点的直线，而反比例函数的图像是一条不通过原点的直线。

正比例和反比例是两种截然不同的函数关系，虽然它们有一些相同点，但更多的是不同点。

在实际问题中，我们需要根据具体情况来判断是应该使用哪种函数形式来描述变量之间的关系。