传送带模型和板块模型96页PPT

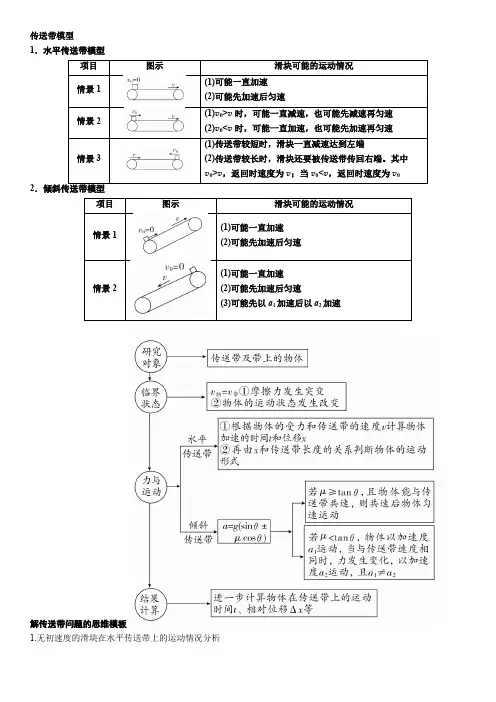
传送带模型1．水平传送带模型(1)(2)(1)(2)(1)(2)返回时速度为2．(1)(2)(1)(2)(3)解传送带问题的思维模板1.无初速度的滑块在水平传送带上的运动情况分析3.无初速度的滑块在倾斜传送带上的运动情况分析4.有初速度的滑块在倾斜传送带上的运动情况分析“传送带”模型和“板—块”模型是近几年高考命题的热点，如2015年全国卷ⅠT25、全国卷ⅡT25、2017年全国卷ⅢT25，都是以“板—块”模型为素材的问题．两类模型涉及弹力及摩擦力的分析判断与计算、牛顿运动定律、匀变速直线运动规律、动量、能量等主干知识，具有条件隐蔽、过程复杂等特点，既能训练学生的科学思维，又能联系科学、生产和生活实际，是很好的能力考查类题目的命题背景．模型一：“传送带”模型[示例1] 某工厂为实现自动传送工件设计了如图所示的传送装置，它由一个水平传送带AB 和倾斜传送带CD 组成，水平传送带长度L AB ＝4 m ，倾斜传送带长度L CD ＝4.45 m ，倾角为θ＝37°，AB 和CD 通过一段极短的光滑圆弧板过渡，AB 传送带以v 1＝5 m /s 的恒定速率顺时针运转，CD 传送带静止．已知工件与传送带间的动摩擦因数均为μ＝0.5，重力加速度g 取10 m/s 2.现将一个工件(可看作质点)无初速度地放在水平传送带最左端A 点处，求：(1)工件被第一次传送到CD 传送带沿传送带上升的最大高度和所用的总时间；(2)要使工件恰好被传送到CD 传送带最上端，CD 传送带沿顺时针方向运转的速度v 2的大小(v 2<v 1)． [思路探究] (1)工件在水平传送带上运动时受到哪几个力作用？工件在水平传送带上做什么运动？ (2)工件到达B 点的速度是多大？(3)工件在倾斜传送带上运动时受到哪几个力作用？(4)工件在倾斜传送带上做什么运动？如何理解第(2)问中“恰好”？ [解析] (1)工件刚放在传送带AB 上时，在摩擦力作用下做匀加速运动，设其加速度大小为a 1，速度增加到v 1时所用时间为t 1，位移大小为x 1，受力分析如图甲所示，则F N1＝mgF f1＝μF N1＝ma 1 联立解得a 1＝5 m/s 2.由运动学公式有t 1＝v 1a 1＝55 s ＝1 sx 1＝12a 1t 21＝12×5×12 m ＝2.5 m由于x 1<L AB ，工件随后在传送带AB 上做匀速直线运动到B 端，则匀速运动的时间为t 2＝L AB －x 1v 1＝0.3 s工件滑上CD 传送带后在重力和滑动摩擦力作用下做匀减速运动，设其加速度大小为a 2，速度减小到零时所用时间为t 3，位移大小为x 2，受力分析如图乙所示，则F N2＝mg cos θmg sin θ＋μF N2＝ma 2 由运动学公式有x 2＝0－v 21－2a 2联立解得a 2＝10 m/s 2，x 2＝1.25 m 工件沿CD 传送带上升的最大高度为 h ＝x 2sin θ＝1.25×0.6 m ＝0.75 m 沿CD 上升的时间为t 3＝0－v 1－a 2＝0.5 s故总时间为t＝t1＋t2＋t3＝1.8 s.(2)CD传送带以速度v2向上传送时，当工件的速度大于v2时，滑动摩擦力沿传送带向下，加速度大小仍为a2；当工件的速度小于v2时，滑动摩擦力沿传送带向上，受力分析图如图丙所示，设其加速度大小为a3，两个过程的位移大小分别为x3和x4，由运动学公式和牛顿运动定律可得－2a2x3＝v22－v21mg sin θ－μF N2＝ma3－2a3x4＝0－v22L CD＝x3＋x4解得v2＝4 m/s.[答案](1)0.75 m 1.8 s(2)4 m/s[规律总结]传送带问题的“三点说明”(1)传送带问题的实质是相对运动问题，物体与传送带间的相对运动方向决定摩擦力的方向．因此，明确物体与传送带间的相对运动方向是解决该问题的关键．(2)传送带问题还常常涉及临界问题，即物体与传送带速度相同，这时会出现摩擦力改变的临界状态，具体如何改变根据具体情况判断．(3)分析求解此类问题的思路[应用提升练]1.如图所示，水平传送带静止不动，质量为1 kg的小物体以4 m/s的水平初速度滑上传送带的左端，最终以2 m/s的速度从传送带的右端滑下．如果令传送带逆时针方向匀速转动，小物体仍然以4 m/s的水平初速度滑上传送带的左端，则小物体离开传送带时()A．速度小于2 m/sB．速度等于2 m/sC．速度大于2 m/sD．不能到达传送带右端解析：当传送带不动时，物体受到向左的滑动摩擦力，在传送带上向右做匀减速运动，最终离开传送带．当传送带逆时针转动时，物体仍然相对传送带向右运动，所以受到的摩擦力仍然向左，与传送带静止时比较，受力情况完全相同，运动情况一致，最后从传送带离开时速度仍然是2 m/s.本题正确答案为B.答案：B2.如图所示为粮袋的传送装置，已知A、B间长度为L，传送带与水平方向的夹角为θ，工作时其运行速度为v，粮袋与传送带间的动摩擦因数为μ，正常工作时工人在A点将粮袋放到运行中的传送带上．关于粮袋从A到B的运动，以下说法正确的是(设最大静摩擦力等于滑动摩擦力)()A．粮袋到达B点的速度可能大于v，可能小于v，还可能等于vB．粮袋开始运动的加速度为g(sin θ－μcos θ)，若L足够大，则以后将一定以速度v做匀速运动C．若μ≥tan θ，则粮袋从A到B一定一直做加速运动D．不论μ大小如何，粮袋从A到B一直做匀加速运动，且a>g sin θ解析：开始时，粮袋相对传送带向上运动，受重力、支持力和沿传送带向下的摩擦力，由牛顿第二定律可知，mg sin θ＋μF N＝ma，F N＝mg cos θ，解得a＝g sin θ＋μg cos θ，故B项错误；粮袋加速到与传送带相对静止时，若mg sin θ>μmg cos θ，即当μ<tan θ时粮袋将继续做匀加速运动，若mg sin θ≤μmg cos θ，即当μ≥tan θ时，粮袋从A到B可能一直做匀加速运动，也可能先做匀加速运动，当速度与传送带相同后做匀速运动，C、D项错误，A项正确．答案：A模型二：“板—块”模型[示例2](2017·高考全国卷Ⅲ)如图，两个滑块A和B的质量分别为m A＝1 kg和m B＝5kg，放在静止于水平地面上的木板的两端，两者与木板间的动摩擦因数均为μ1＝0.5；木板的质量为m＝4 kg，与地面间的动摩擦因数为μ2＝0.1.某时刻A、B两滑块开始相向滑动，初速度大小均为v0＝3 m/s.A、B相遇时，A与木板恰好相对静止．设最大静摩擦力等于滑动摩擦力，取重力加速度大小g＝10 m/s2.求：(1)B与木板相对静止时，木板的速度；(2)A、B开始运动时，两者之间的距离．[思路探究](1)A、B在木板上滑动时，木板所受的力有哪些？木板做什么运动？(2)A、B哪一个先与木板共速？共速后各自做什么运动？[解析](1)滑块A和B在木板上滑动时，木板也在地面上滑动．设A、B所受的摩擦力大小分别为f1、f2，木板所受地面的摩擦力大小为f3，A和B相对于地面的加速度大小分别为a A和a B，木板相对于地面的加速度大小为a1.在物块B与木板达到共同速度前有f1＝μ1m A g①f2＝μ1m B g②f3＝μ2(m＋m A＋m B)g③由牛顿第二定律得f1＝m A a A④f2＝m B a B⑤f2－f1－f3＝ma1⑥设在t1时刻，B与木板达到共同速度，其大小为v1.由运动学公式有v1＝v0－a B t1⑦v1＝a1t1⑧联立①②③④⑤⑥⑦⑧式，代入已知数据得v1＝1 m/s⑨(2)在t1时间间隔内，B相对于地面移动的距离为s B ＝v 0t 1－12a B t 21⑩设在B 与木板达到共同速度v 1后，木板的加速度大小为a 2.对于B 与木板组成的体系，由牛顿第二定律有f 1＋f 3＝(m B ＋m )a 2⑪由①②④⑤式知，a A ＝a B ；再由⑦⑧式知，B 与木板达到共同速度时，A 的速度大小也为v 1，但运动方向与木板相反．由题意知，A 和B 相遇时，A 与木板的速度相同，设其大小为v 2.设A 的速度大小从v 1变到v 2所用的时间为t 2，则由运动学公式，对木板有v 2＝v 1－a 2t 2⑫ 对A 有v 2＝－v 1＋a A t 2⑬在t 2时间间隔内，B (以及木板)相对地面移动的距离为s 1＝v 1t 2－12a 2t 22⑭在(t 1＋t 2)时间间隔内，A 相对地面移动的距离为 s A ＝v 0(t 1＋t 2)－12a A (t 1＋t 2)2⑮A 和B 相遇时，A 与木板的速度也恰好相同． 因此A 和B 开始运动时，两者之间的距离为 s 0＝s A ＋s 1＋s B ⑯联立以上各式，并代入数据得s 0＝1.9 m ⑰ (也可用如图所示的速度—时间图线求解)[答案] (1)1 m/s (2)1.9 m[规律总结]分析“板—块”模型的四点注意(1)从速度、位移、时间等角度，寻找滑块与滑板之间的联系． (2)滑块与滑板共速是摩擦力发生突变的临界条件． (3)滑块与滑板存在相对滑动的临界条件①运动学条件：若两物体速度不等，则会发生相对滑动．②力学条件：一般情况下，假设两物体间无相对滑动，先用整体法算出一起运动的加速度，再用隔离法算出滑块“所需要”的摩擦力F f ，比较F f 与最大静摩擦力F fm 的关系，若F f >F fm ，则发生相对滑动．(4)滑块不从滑板上掉下来的临界条件是滑块到达滑板末端时，两者共速．[应用提升练]3．(多选)(2018·湖南邵阳高三质检)如图甲所示，一质量为m ′的长木板静置于光滑水平面上，其上放置一质量为m 的小滑块．木板受到水平拉力F 作用时，用传感器测出长木板的加速度a 与水平拉力F 的关系如图乙所示，重力加速度g 取10 m/s 2，下列说法正确的是( )A ．小滑块的质量m ＝2 kgB ．小滑块与长木板之间的动摩擦因数为0.1C ．当水平拉力F ＝7 N 时，长木板的加速度大小为3 m/s 2D ．当水平拉力F 增大时，小滑块的加速度一定增大解析：对整体分析，由牛顿第二定律有F ＝(m ′＋m )a ，当F ＝6 N 时，此时两物体具有最大共同加速度，代入数据解得m ′＋m ＝3 kg ，当F 大于6 N 时，根据牛顿第二定律得a ＝F －μmg m ′＝F m ′－μmg m ′，知图线的斜率k ＝1m ′＝1，解得m ′＝1 kg ，小滑块的质量为m ＝2 kg ，故A 正确；根据图象可知，μmg ＝4 N ，代入数据解得μ＝0.2，所以a 与F 的数值关系为a ＝F －4，当F ＝7 N 时，长木板的加速度为a ＝3 m/s 2，故B 错误，C 正确；当拉力增大到一定的值后，两物体发生滑动时，小滑块的加速度为a ′＝μmgm ＝2 m/s 2，即使拉力再增大，小滑块的加速度也不变，故D 错误．答案：AC4．如图所示，有两个高低不同的水平面，高水平面光滑，低水平面粗糙．一质量为5 kg 、长度为2 m 的长木板靠在低水平面边缘，其表面恰好与高水平面平齐，长木板与低水平面间的动摩擦因数为0.05，一质量为1 kg 可视为质点的滑块静止放置在高水平面上，距边缘A 点3 m ，现用大小为6 N 、水平向右的外力拉滑块，当滑块运动到A 点时撤去外力，滑块以此时的速度滑上长木板．滑块与长木板间的动摩擦因数为0.5，g 取10 m/s 2.求：(1)滑块滑动到A 点时的速度大小；(2)滑块滑动到长木板上时，滑块和长木板的加速度大小分别为多少？ (3)通过计算说明滑块能否从长木板的右端滑出． 解析：(1)根据牛顿第二定律有F ＝ma 根据运动学公式有v 2＝2aL 0 联立方程代入数据解得v ＝6 m/s其中m 、F 分别为滑块的质量和受到的拉力，a 是滑块的加速度，v 即是滑块滑到A 点时的速度大小，L 0是滑块在高水平面上运动的位移．(2)根据牛顿第二定律， 对滑块有μ1mg ＝ma 1 代入数据解得a 1＝5 m/s 2对长木板有μ1mg －μ2(m ＋M )g ＝Ma 2 代入数据解得a 2＝0.4 m/s 2.其中M 为长木板的质量，a 1、a 2分别是此过程中滑块和长木板的加速度，μ1、μ2分别是滑块与长木板间和长木板与低水平面间的动摩擦因数．(3)设滑块滑不出长木板，从滑块滑上长木板到两者相对静止所用时间为t ，则 v －a 1t ＝a 2t代入数据解得t ＝109s则此过程中滑块的位移为x 1＝v t －12a 1t 2长木板的位移为x 2＝12a 2t 2x 1－x 2＝103m>L式中L ＝2 m 为长木板的长度，所以滑块能滑出长木板右端． 答案：(1)6 m /s (2)5 m/s 2 0.4 m/s 2 (3)见解析。