一元二次方程单元结构图

一元二次方程主题单元设计主题单元规划思维导图（说明：将主题单元规划的思维导图导出为jpeg 文件后，粘贴在这里；如果提交到平台，则需要使用图片导入的功能，具体操作见《2013学员教师远程研修手册》。

）主题单元学习目标（说明：依据新课程标准要求描述学生在本主题单元学习中所要达到的主要目标）知识与技能：了解一元二次方程及有关概念；掌握通过配方法、公式法、因式分解法降次──解一元二次方程；掌握依据实际问题建立一元二次方程的数学模型的方法；应用熟练掌握以上知识解决问题．过程与方法：（1）通过丰富的实例，让学生合作探讨，老师点评分析，建立数学模型．•根据数学模型恰如其分地给出一元二次方程的概念．（2）结合整式中的有关概念介绍一元二次方程的概念，如二次项等．（3）通过掌握缺一次项的一元二次方程的解法──直接开方法，•导入用配方法解一元二次方程，又通过大量的练习巩固配方法解一元二次方在学习活动中获得成功的体验，建立学好数学的信心。

专题问题设计1、用观察检验法估计一元二次方程的解2、配方法的一般形式是什么？配方法的一般步骤3、公式法的公式是什么？b2-4ac>0，b2-4ac=0，b2-4ac<0的解的情况？4、因式分解法的一般思路是什么?5、一元二次方程如何选择方程的解法？所需教学环境和教学资源信息化资源：计算机常规资源：教材、多媒体课件、几何画板课件教学支撑环境：多媒体教室学习活动设计第一课时用配方法解一元二次方程活动1：用配方法解一元二次方程（二次项的系数为1）1、用配方法解下列关于x的方程（1）x2-8x+1=0 （2）x2-2x-=0问题：已知ax2+bx+c=0（a≠0），试推导它的两个根x1=，x2=(这个方程一定有解吗?什么情况下有解？)活动2：用公式法解一元二次方程1、用公式法解下列方程．（1）2x2-x-1=0 （2）x2+1.5=-3x3、要求学生对知识整体认识的基础上，对知识进行巩固提高4、整理自己的想法和做法，在小组内表述自己的探索过程和结论．活动3：拓展提高：某数学兴趣小组对关于x的方程（m+1）+（m-2）x-1=0提出了下列问题．若使方程为一元二次方程，m是否存在？若存在，求出m并解此方程。

一元二次方程,表格一元二次方
程知道y求x
1. excel一元二次方程知道y求x
右键单击图形添加趋势线类型线性选项显示公式确定图表上即得到你要的直线表达式也就得到了k和b的值
2. 如何用excel求一元二次方程
先来看看用excel求解一元一次方程的方法新建一个excel文档，使用a1单元格放置未知数x，先什么都不填，使这个单元格保持空白。

将x的系数10填入a3单元格，将等号左边的常数项-10填入b3单元格，把等号右边的常数项110填入c3单元格。

将这些数填好后，在单元格d3中输入方程式左边的公式“=$a$1*a3+b3”，按一下回车键，这是可以看到d3单元格中会显示-10，由于a1单元格中现在没有数据，按0处理。

打开工具菜单，选择单变量求解选项，会弹出单变量求解对话框。

目标单元格中默认输入了d3，这个单元格表示方程式等号左边的内容，在目标值后面的输入框中，输入110，也就是方程右边的值点击可变单元格输入框后面的按钮，在excel工作表中选择表示未知数x的单元格a1。

再单击输入框后面的按钮，回到单变量求解对话框单击确定按钮现在方程的解x的值12已经填在a1单元格中了同时还弹出了单变量求解状态对话框怎么样？这就是用excel求解一元一次方程的操作步骤，还挺简单的吧！你可以把这个文件存为一个模板文件以后解一元一次方程的时候打开这个文件替换相应位置的数字就可以了。

3. excel求一元二次方程
可以写出一堆 ax by=c 的方程用excel怎么生成一元一次方程 : 1.打开excel界面。

2.输入数表格。

3.点击数据--数据分析。

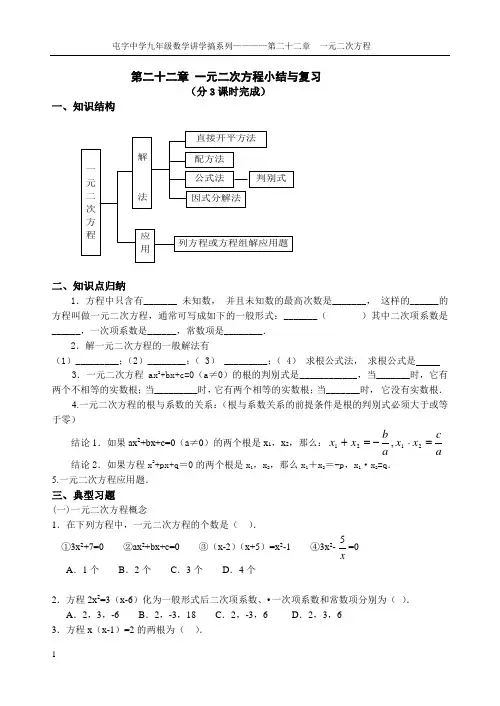
第二十二章 一元二次方程小结与复习（分3课时完成）一、知识结构二、知识点归纳1．方程中只含有_______•未知数，•并且未知数的最高次数是_______，•这样的______的方程叫做一元二次方程，通常可写成如下的一般形式：_______（ ）其中二次项系数是______，一次项系数是______，常数项是________．2．解一元二次方程的一般解法有（1）_________；（2）________；（•3）•_________；（•4）•求根公式法，•求根公式是3．一元二次方程ax 2+bx+c=0（a ≠0）的根的判别式是____________，当_______时，它有两个不相等的实数根；当_________时，它有两个相等的实数根；当_______时，•它没有实数根．4.一元二次方程的根与系数的关系：（根与系数关系的前提条件是根的判别式必须大于或等于零）结论1．如果ax 2+bx+c=0（a ≠0）的两个根是x 1，x 2，那么： 结论2．如果方程x 2+px+q ＝0的两个根是x 1，x 2，那么x 1＋x 2＝-p ，x 1·x 2=q ． 5.一元二次方程应用题．三、典型习题(一)一元二次方程概念1．在下列方程中，一元二次方程的个数是（ ）．①3x 2+7=0 ②ax 2+bx+c=0 ③（x-2）（x+5）=x 2-1 ④3x 2-=0 A ．1个 B ．2个 C ．3个 D ．4个2．方程2x 2=3（x-6）化为一般形式后二次项系数、•一次项系数和常数项分别为（ ）．A ．2，3，-6B ．2，-3，18C ．2，-3，6D ．2，3，6 3．方程x （x-1）=2的两根为（ ）．acx x a b x x =⋅-=+2121,5xA ．x 1=0，x 2=1B ．x 1=0，x 2=-1C ．x 1=1，x 2=2D ．x 1=-1，x 2=2 4．已知x=-1是方程ax 2+bx+c=0的根（b ≠0），则（ ）． A ．1B ．-1C ．0D ．25．方程3x 2-3=2x+1的二次项系数为________，一次项系数为_________，常数项为_________． 6．一元二次方程的一般形式是 ．7．关于x 的方程（a-1）x 2+3x=0是一元二次方程，则a 的取值范围是________． 8．已知方程5x 2+mx-6=0的一个根是x=3，则m 的值为________．9．a 满足什么条件时，关于x 的方程a （x 2+x ）x-（x+1）是一元二次方程？10．关于x 的方程（2m 2+m ）x m+1+3x=6可能是一元二次方程吗？为什么？11．如果x=1是方程ax 2+bx+3=0的一个根，求（a-b ）2+4ab 的值．（二）解一元二次方程的方法：1．将二次三项式x 2-4x+1配方后得（ ）．A ．（x-2）2+3B ．（x-2）2-3C ．（x+2）2+3D ．（x+2）2-3 2．已知x 2-8x+15=0，左边化成含有x 的完全平方形式，其中正确的是（ ）． A ．x 2-8x+（-4）2=31 B ．x 2-8x+（-4）2=1 C ．x 2+8x+42=1 D ．x 2-4x+4=-11 3．方程x 2+4x-5=0的解是________．4．代数式的值为0，则x 的值为________． 5．无论x 、y 取任何实数，多项式x 2+y 2-2x-4y+16的值总是_______数． 6．如果16（x-y ）2+40（x-y ）+25=0，那么x 与y 的关系是________．7．一元二次方程ax 2+bx+c=0（a ≠0）的求根公式是________，条件是________． 8．当x=______时，代数式x 2-8x+12的值是-4．9．已知方程x 2+px+q=0有两个相等的实数，则p 与q 的关系是________．10．已知b ≠0，不解方程，试判定关于x 的一元二次方程x 2-（2a+b ）x+（a+ab-2b 2）•=0的根的情况是________． 11．如果x 2-4x+y 2+13=0，则（xy ）z •=2221x x x ---12.某数学兴趣小组对关于x 的方程（m+1）+（m-2）x-1=0提出了下列问题．（1）若使方程为一元二次方程，m 是否存在？若存在，求出m 并解此方程． （2）若使方程为一元一次方程m 是否存在？若存在，请求出．13.用直接开平方法解下列方程（1）3x 2+9=0 （2）8x 2-16=0 （3）（x-）2=2（x-3）2=7214．用配方法解下列方程 （1）x 2-8x+1=0 （2）x 2-2x-=0 （3）9y 2-18y-4=0 （4）x 215.用公式法解下列方程．（1）2x 2-x-1=0 （2）x 2+1.5=-3x (3) x 2x+=0 （4）4x 2-3x+2=016．用因式分解法解下列方程．（1）3y 2-6y=0 （2）25y 2-16=0 （3）x 2-12x-28=0 （4）x 2-12x+35=017.不解方程，判定方程根的情况（1）16x 2+8x=-3 （2）9x 2+6x+1=0 （3）2x 2-9x+8=0 （4）x 2-7x-18=0 18.不解方程，写出下列方程的两根和与两根积：22m x+13891212013)1(2=--x x 0532)2(2=-+x x 02231)3(=-x x。

1 实际问题设未知识，列方程
数学问题
ax 2+bx+c=0(a ≠0)
解
方
程开平方法配方法↓
公式法
因式分解法降次实际问题的答案数学问题的解决
X=242ac
b
b 检验一元二次方程教材分析
一、本章知识结构框图
二、本章的地位和作用
1、一元二次方程是中学数学的主要内容，在初中代数中占有重要的地位，学习本章内容是对一元一次方程学习的扩展。

2、一元二次方程可以解决更为广泛的实际问题，为后续学习起到重要作用，学习一元二次方程对学习其它学科有重要意义。

三、教学目标
（一）知识与技能
1、理解一元二次方程及其有关概念。

2、掌握一元二次方程的解法，会根据具体的一元二次方程的不同的特点选择适当的解法，会用一元二次方程根的判别式判别根的情况，会用根与系数的关系定理解决有关的简单问题。

3、能用一元二次方程解决实际问题，能根据具体问题的实际意义检验结果的合。