当前位置：文档之家 › 信号与系统答案 西北工业大学 段哲民 第五章

信号与系统答案 西北工业大学 段哲民 第五章

  • 格式：pdf
  • 大小：252.53 KB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

信号与系统第五章习题答案

信号与系统第五章习题答案

i = −∞ i= 0
∞
n− 6
1 − a n− 5 ε [n − 6 ] 1− a
故系统的零状态响应为
y zs [n ] = f [n] ∗ h[n] = a n ε [n] ∗ (ε [n] − ε [n − 6]) = a n ε [n] ∗ ε [n ] − a nε [n] ∗ ε [n − 6]
联立以上两式可解得： A1 = 1 ， A2 = 2 于是齐次解为
275
y h [n] = (− 3) + 2 n+1
n
5.10
如有齐次差分方程为 y[n] + 4 y[n − 1] + 4 y[n − 2] = 0 ， 已知 y[0] = y[1] = −2 ， 试求其齐次解。 【知识点窍】主要考察系统的齐次解的概念及其求解方法。 【逻辑推理】首先通过差分方程得特征方程，由特征方程求得特征根，代入条件即可求得齐次
λ2 + 3λ + 2 = 0
y zi [n ] = A1 (− 1) + A2 (− 2)
n
n
将初始状态 y[− 1] = −
1 , 2
y[− 2] =
5 代入上式，有： 4
−1 −1
y[− 1] = y zi [− 1] = A1 (− 1) + A2 (− 2 ) = − y[− 2] = y zi [− 2 ] = A1 (− 1) + A2 (− 2 )
−2 −2
1 2 5 = 4
271
联立以上两式可解得： A1 = 2 ， A2 = −3 则系统的零输入响应为
y zi [n ] = 2(− 1) − 3(− 2)
n
n
5.4 设有离散系统的差分方程为 y[n] + 4 y[n − 1] + 3 y[n − 2] = 4 f [n] + f [n − 1] ，试画出其时域模拟 图。 【知识点窍】主要考察由系统的差分方程画出系统的直接模拟图，掌握直接模拟图的意义。 【逻辑推理】将差分方程各个环节分别用加法器及延时器来表示。 解：时域模拟图如图 5.1
信号与系统第五章习题

信号与系统第五章习题


03
零极点与系统频率 响应的关系
了解系统零极点与系统频率响应 的关系，掌握通过零极点分析系 统频率响应的方法。
复频域特性分析
复频域中的系统特性
理解复频域中系统的特性，如幅频特性、相频 特性等。
幅频特性与相频特性的求解
掌握幅频特性与相频特性的求解方法，包括直 接计算法、图形法等。
系统稳定性的复频域判据
03 频域分析习题讲解
周期信号频谱分析
01
周期信号的频谱是离散的，由基频和各次谐波组成。
02
周期信号的频谱可以通过傅里叶级数展开得到，其中傅里叶 系数与频谱幅度和相位有关。
03
周期信号的频谱具有收敛性，即高频分量的幅度逐渐减小。
非周期信号频谱分析
01
非周期信号的频谱是连续的，由无穷多个频率分量组
了解系统稳定性的复频域判据，如奈奎斯特稳定判据等。
05 离散时间信号与系统习题 讲解
离散时间信号表示与运算规则
01
离散时间信号的定义 和表示方法
离散时间信号是一系列在离散时刻上 取值的信号，可以用序列或函数表示 。常见的表示方法有图形表示、解析 式表示和表格表示等。
02
离散时间信号的基本 运算
包括信号的相加、相乘、时移、反折 和尺度变换等基本运算。这些运算在 信号处理中具有重要的应用，如信号 的合成、分解、调制和解调等。
傅里叶变换的性质
熟练运用傅里叶变换的线性、时移、频移、共轭等性质 进行信号分析和处理。
ABCD
频域信号的物理意义
掌握频域信号如何表示时域信号中的频率成分及其幅度 和相位信息。
能量谱与功率谱的计算
掌握如何根据信号的傅里叶变换计算其能量谱或功率谱 。
习题类型及解题思路
[工学]信号与系统答案西北工业大学段哲民信号与系统1-3章答案

[工学]信号与系统答案西北工业大学段哲民信号与系统1-3章答案

[⼯学]信号与系统答案西北⼯业⼤学段哲民信号与系统1-3章答案[⼯学]信号与系统答案西北⼯业⼤学段哲民信号与系统1-3章答案第⼀章习题-t1-1 画出下列各信号的波形:(1) f(t)=(2-e)U(t); (2) 1-tf(t)=ecos10πt×[U(t-1)-U(t-2)]。

2答案f(t)1 (1)的波形如图1.1(a)所⽰.,2T,,0.2sf(t)cos10,t,102(2) 因的周期,故的波形如图题1.1(b)所⽰.1-2 已知各信号的波形如图题1-2所⽰，试写出它们各⾃的函数式。

答案f(t),t[u(t),u(t,1)]，u(t,1)1f(t),,(t,1)[u(t),u(t,1)]2f(t),(t,2)[u(t,2),u(t,3)]31-3 写出图题1-3所⽰各信号的函数表达式。

答案11,(t，2),t，1,2,t,0,22f(t),,1110,t,2,(,t，2),,t，122,f(t),u(t)，u(t,1)u(t,2)2,f(t),,sint[u(t，2),u(t,2)]32f(t),u(t，2),2u(t，1)，3u(t,1),4u(t,2)，2u(t,3)421-4 画出下列各信号的波形:(1) f(t)=U(t-1); (2) f(t)=(t-1)U(t-1); 1222(3) f(t)=U(t-5t+6); (4)f(t)=U(sinπt)。

34答案f(t),u(t,1)，u(,t,1)1 (1) ,其波形如图题1.4(a)所⽰.f(t),(t,1)[u(t,1)，u(,t,1)],(t,1)u(t,1)，(t,1)u(,t,1)2(2)其波形如图题1.4(b)所⽰.f(t),u(,t，2)，u(t,3)3(3) ,其波形如图1.4(c)所⽰.f(t),u(sin,t)4(4) 的波形如图题1.4(d)所⽰.1-5 判断下列各信号是否为周期信号，若是周期信号，求其周期T。

信号与系统第五章_课后答案

信号与系统第五章_课后答案

信号与系统第五章课后答案信号与系统课后答案操作系统课后答案信号与系统答案信号与系统习题答案课后答案网课后习题答案网土力学课后习题答案课后答案综合教程3课后答案
课后答案网，用心为你服务！
大学答案 --- 中学答案 --- 考研答案 --- 考试答案 最全最多的课后习题参考答案，尽在课后答案网（）！ Khdaw团队一直秉承用心为大家服务的宗旨，以关注学生的学习生活为出发点， 旨在为广大学生朋友的自主学习提供一个分享和交流的平台。 爱校园（） 课后答案网（） 淘答案（）
ww w. kh
课
da w
案 网
后 答
.c om
ww w. kh
课
da w
案 网
后 答
.c om
ww w. kh
课
da w
案 网
后 答
.c om
ww w. kh
课
da w
案 网
后 答
.c om
ww w. kh
课
da w
案 网
Hale Waihona Puke 后 答.c omww w. kh
课
da w
案 网
后 答
.c om
信号与系统课后习题答案第5章

信号与系统课后习题答案第5章

全响应:
y(k)=［2(－1)k+(k－2)(－2)k］ε(k)
76
第5章 离散信号与系统的时域分析
5.23 求下列差分方程所描述的离散系统的零输入响应、 零状态响应和全响应。
77
第5章 离散信号与系统的时域分析 78
第5章 离散信号与系统的时域分析
确定系统单位响应: 由H(E)极点r=－2, 写出零输入响应表示式: 将初始条件yzi(0)=0代入上式，确定c1=0, 故有yzi(k)=0。
题解图 5.6-1
16
第5章 离散信号与系统的时域分析
题解图 5.6-2
17
第5章 离散信号与系统的时域分析
因此
18
第5章 离散信号与系统的时域分析
5.7 各序列的图形如题图 5.2 所示，求下列卷积和。
题图 5.2
19
第5章 离散信号与系统的时域分析 20
第5章 离散信号与系统的时域分析 21
第5章 离散信号与系统的时域分析 46
第5章 离散信号与系统的时域分析
5.16 已知离散系统的差分方程(或传输算子)如下，试求各 系统的单位响应。
47
第5章 离散信号与系统的时域分析 48
由于
第5章 离散信号与系统的时域分析
49
第5章 离散信号与系统的时域分析
因此系统单位响应为
50
第5章 离散信号与系统的时域分析 51
5.21 已知LTI离散系统的单位响应为
试求： (1) 输入为
时的零状态响应yzs(k)； (2) 描述该系统的传输算子H(E)。
69
第5章 离散信号与系统的时域分析
解 (1) 由题意知: 先计算:
70
第5章 离散信号与系统的时域分析
信号与系统课后习题答案第5章

信号与系统课后习题答案第5章

代入初始条件yzi(0)=1,确定c=1,故有零输入响应:
yzi(k)=(－2)kε(k)
39
第5章 离散信号与系统的时域分析 40
第5章 离散信号与系统的时域分析 41
第5章 离散信号与系统的时域分析 42
第5章 离散信号与系统的时域分析 43
第5章 离散信号与系统的时域分析
(6) 系统传输算子:
22
第5章 离散信号与系统的时域分析
5.9 已知两序列
试计算f1(k)*f2(k)。
23
解 因为
第5章 离散信号与系统的时域分析
所以
24
第5章 离散信号与系统的时域分析
5.10 已知序列x(k)、y(k)为
试用图解法求g(k)=x(k)*y(k)。
25
第5章 离散信号与系统的时域分析
解 首先画出y(k)和x(k)图形如题解图5.10所示, 然后结合 卷积和的图解机理和常用公式,应用局部范围等效的计算方法 求解。
题解图 5.10
26
第5章 离散信号与系统的时域分析 27
总之有
第5章 离散信号与系统的时域分析
28
第5章 离散信号与系统的时域分析
5.11 下列系统方程中，f(k)和y(k)分别表示系统的输入和输 出，试写出各离散系统的传输算子H(E)。
29
第5章 离散信号与系统的时域分析
解 由系统差分方程写出传输算子H(E)如下:
解 各序列的图形如题解图5.2所示。
题解图 5.2
5
第5章 离散信号与系统的时域分析
5.3 写出题图 5.1 所示各序列的表达式。
题图 5.1
6
第5章 离散信号与系统的时域分析 7
第5章 离散信号与系统的时域分析
《信号与系统》第五章基本内容示例(含答案)

《信号与系统》第五章基本内容示例(含答案)


e−4t
sin(0t)
(t)
（2）ℒ
(2t
−
5)
=
1
−5s
e2
s
（3）ℒ-1
1 1− e−s
=
k =0
(t
−
k)
（4）ℒ
cos(3t − 2) (3t − 2) =
s
2
s +
9
−
e
2 3
s
（5）ℒ
e−t (t)
− e−(t −3)
(t
−
3)
=
s
1 (1− +1
e−3s )
（6）ℒ-1
1 2
2. 已知系统的 H (s) = s +1 ，画出系统的零、极点分布图。
(s + 2)2 + 4
六、简单计算下列式子
ℒ 1、
-1
(s
+
0 4)2
+
02
2、ℒ (2t − 5)
ℒ-1
3、
1
1 − e−
s
4、ℒ cos(3t − 2) (3t − 2)
ℒ 5、 e−t (t) − e−(t −3) (t − 3)
系统并联后的复合系统的系统函数为（ ）。
A ． H1(s) + H2 (s)
B ． H1(s) H2(s)
C．无法确定
D． H1(s) // H2(s) 14、若 f (t) 1 ，Re[s] −3 ，根据终值定理，原函数 f (t) 的终值为
s+3
（ ）。
A．无穷小
B．无穷大
C． 1 D． 0
X (s) = F(s) + s X (s) + s2 X (s)
信号与系统_西北工业大学中国大学mooc课后章节答案期末考试题库2023年

信号与系统_西北工业大学中国大学mooc课后章节答案期末考试题库2023年

信号与系统_西北工业大学中国大学mooc课后章节答案期末考试题库2023年1.所以非周期信号都是能量信号。

参考答案:错误2.连续周期信号的傅里叶级数是（）参考答案:离散的3.所有连续的周期信号的频谱都具有收敛性。

参考答案:错误4.状态方程和输出方程共同构成了描述系统特征的完整方程。

参考答案:正确5.连续系统状态变量的个数等于动态元件数。

参考答案:错误6.一个信号存在傅氏变换，则一定存在双边拉氏变换。

参考答案:正确7.周期奇函数的傅里叶级数中，只含有（）参考答案:正弦项8.理想低通滤波器是一个因果系统。

参考答案:错误9.没有信号可以既是有限长的同时又有带限的频谱。

参考答案:正确10.一个信号存在傅氏变换，则一定存在单边拉氏变换。

参考答案:错误11.一个信号存在拉氏变换，则一定存在傅氏变换。

参考答案:错误12.下列叙述正确的是（）参考答案:一个信号存在傅立叶变换，就一定存在双边拉普拉斯变换。

13.非周期连续时间信号的频谱是连续频率的非周期函数。

参考答案:正确14.状态变量在某一确定时刻的值，即为系统在时刻的状态。

参考答案:正确15.状态空间分析法可以推广至非线性和时变系统。

参考答案:正确16.下面的各种描述，正确的是（）参考答案:若零、极点离虚轴很远，则它们对频率响应的影响非常小。

17.状态空间分析法可以用于多输入多输出系统分析，也可用于但输入单输出系统的分析。

参考答案:正确18.周期信号的频谱一定是（）参考答案:离散谱19.两个非线性系统级联构成的系统是非线性的。

参考答案:错误。

信号与系统答案 西北工业大学 段哲民 第五章

信号与系统答案 西北工业大学 段哲民 第五章

3e − 2t + (−2)te − 2t = (3 − 2t )e − 2t
[
]
故
f (t ) = e −3t + (3 − 2t )e −2t U (t )
[
]
+ 5.6 求下列各像函数 F (s ) 的原函数 f (t ) 的初值 f (0 ) 与终值 f (∞ ) 。
(1) F (s ) =
1 s + 3 ，代入上式有
令
F (s) =
( s 2 + 3s + 2)Y f ( s ) = s
1 s + 3s + 2
2
1 1 +3 =1 s+3 s+3
故
Y f (s) =
故得零状态响应 y f (t ) 的初始值为
y f (0 + ) = lim s
s →∞
1 =0 s + 3s + 2
(2)
F (s) =
s sinψ + ω cosψ s2 + ω
F ( s) =
(3)
s (s + α )2
F ( s) =
(4)
1
α
×
α
s(s + α )
=
1 s( s + α )
(5)
F (s) =
2 s2
(6) (7)
F ( s) =
1 2 3s 2 + 2 s + 1 + + 3 = s2 s s2
Re s 2 =
1 ⎧d st ⎫ = ⎨ F ( s)(s + 2)e ⎬ (2 − 1)! ⎩ dt ⎭ s = −2
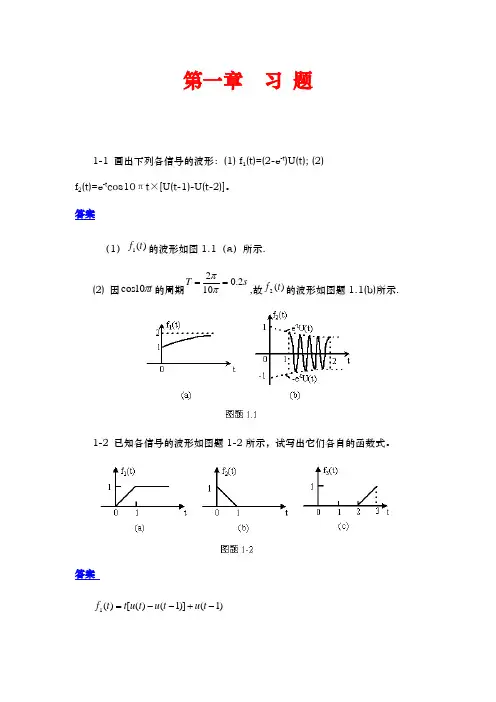
信号与系统答案西北工业大学段哲民信号与系统1_3章答案

信号与系统答案西北工业大学段哲民信号与系统1_3章答案

第一章 习 题1-1 画出下列各信号的波形：(1) f 1(t)=(2-e -t )U(t); (2) f 2(t)=e -t cos10πt ×[U(t-1)-U(t-2)]。

答案（1）)(1t f 的波形如图1.1（a ）所示.(2) 因t π10cos 的周期s T 2.0102==ππ,故)(2t f 的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示，试写出它们各自的函数式。

答案)1()]1()([)(1-+--=t u t u t u t t f)]1()()[1()(2----=t u t u t t f)]3()2()[2()(3----=t u t u t t f1-3 写出图题1-3所示各信号的函数表达式。

答案2002121)2(21121)2(21)(1≤≤≤≤-⎪⎩⎪⎨⎧+-=+-+=+=t t t t t t t f)2()1()()(2--+=t u t u t u t f)]2()2([2sin )(3--+-=t u t u t t f π)3(2)2(4)1(3)1(2)2()(4-+---++-+=t u t u t u t u t u t f1-4 画出下列各信号的波形：(1) f 1(t)=U(t 2-1); (2) f 2(t)=(t-1)U(t 2-1); (3) f 3(t)=U(t 2-5t+6); (4)f 4(t)=U(sin πt)。

答案(1) )1()1()(1--+-=t u t u t f ,其波形如图题1.4(a)所示.(2))1()1()1()1()]1()1()[1()(2---+--=--+--=t u t t u t t u t u t t f 其波形如图题1.4(b)所示.(3))3()2()(3-++-=t u t u t f ,其波形如图1.4(c)所示.(4) )(sin )(4t u t f π=的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号，若是周期信号，求其周期T 。

信号与系统课后答案第五章作业答案_第三次

信号与系统课后答案第五章作业答案_第三次


其极点全部在左半平面，故系统稳定。（注：可以采用罗斯-霍尔维兹准则进行判决，但比较 麻烦）
（3）由于其分母多项式 A( s) = s3 − 4s2 − 3s + 2 中 ai 的符号不完全相同，故不满足霍
尔维兹多项式的必要条件，所以系统不稳定。
5-17 某系统的零极点图如题图 5-18 所示，且单位冲激响应 h(t) 的初值 h(0+ ) = 5 ，试写出
↔
H
(s)
=
1 s
−
s
1 +
2
=
s2
2 +
2s
=
Y F
(s) (s)
得：
(s2 + 2s)Y (s) = 2F (s) ⇒ s2Y (s) + 2sY (s) = 2F (s)
故系统的微分方程为：
y ''(t ) + 2 y '(t ) = 2 f (t )
5-26 某反馈系统如题图 5-26 所示，试求：
+
−4 / 3 s+5
( ) ( ) = 4s−1 / 3 + s−2 + −4s−1 / 3 1− −2s−1 1− −5s−1
其信号流图如下图所示
s −1
F (s)
s −1
Y (s)
s −1
与级联形式相类似，分解不同，其信号流图及模拟图都有所变化。
5-16 试判断下列系统的稳定性：
（1）
H (s)
s2Y (s) + 4sY (s) + 3Y (s) = sX (s) + 2X (s)
则
H
(s)
=
Y (s) X (s)

[工学]信号与系统答案 西北工业大学 段哲民 信号与系统1-3章答案

[工学]信号与系统答案西北工业大学段哲民信号与系统1-3章答案第一章习题-t1-1 画出下列各信号的波形:(1) f(t)=(2-e)U(t); (2) 1-tf(t)=ecos10πt×[U(t-1)-U(t-2)]。

2答案f(t)1 (1)的波形如图1.1(a)所示.,2T,,0.2sf(t)cos10,t,102(2) 因的周期,故的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示，试写出它们各自的函数式。

答案f(t),t[u(t),u(t,1)]，u(t,1)1f(t),,(t,1)[u(t),u(t,1)]2f(t),(t,2)[u(t,2),u(t,3)]31-3 写出图题1-3所示各信号的函数表达式。

答案11,(t，2),t，1,2,t,0,22f(t),,1110,t,2,(,t，2),,t，122,f(t),u(t)，u(t,1)u(t,2)2,f(t),,sint[u(t，2),u(t,2)]32f(t),u(t，2),2u(t，1)，3u(t,1),4u(t,2)，2u(t,3)421-4 画出下列各信号的波形:(1) f(t)=U(t-1); (2) f(t)=(t-1)U(t-1); 1222(3) f(t)=U(t-5t+6); (4)f(t)=U(sinπt)。

34答案f(t),u(t,1)，u(,t,1)1 (1) ,其波形如图题1.4(a)所示.f(t),(t,1)[u(t,1)，u(,t,1)],(t,1)u(t,1)，(t,1)u(,t,1)2(2)其波形如图题1.4(b)所示.f(t),u(,t，2)，u(t,3)3(3) ,其波形如图1.4(c)所示.f(t),u(sin,t)4(4) 的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号，若是周期信号，求其周期T。

,,2(1)f(t),2cos(2t,)(1)f(t),[sin(t,)]1246; ; (3) f(t),3cos2,tU(t)3。

(仅供参考)信号与系统课后答案第五章作业答案-第三次

可以采用罗斯霍尔维兹准则进行判决但比较麻烦3由于其分母多项式的符号不完全相同故不满足霍尔维兹多项式的必要条件所以系统不稳定
5-9 用拉普拉斯变换方法求下列微分方程描述的系统冲激响应 h (t ) 和阶跃响应 g (t )
（2）
d2 y(t) dt 2
+
4
dy (t ) dt
+
3 y (t )
=
dx(t) dt
s
)
=
1
0.5s + 0.5s
⋅
(1 (1 +
+ 0.5s) / /0.2 0.5s) / /0.2 +
1
⋅U
s
(
s
)
s
由于
us
(t
)
=
10u
(t
)
↔
10 s
，故
0.2 + 0.1s
U
L
(
s
)
=
0.5s 1+ 0.5s
⋅
(1+ 0.5s) / /0.2 (1+ 0.5s) / /0.2 +
1
⋅
10 s
(s)
=
sy
(0−
)
+ y' (0− s2 + 4s
) + 4y +3
(0−
)
，代入已知条件并求其
逆变换得系统的零输入响应
( ) Yx
(s)
=
s2
s +
+5 4s +
3
=
−1 s+3
+
s
2 +1
↔

《信号与系统》第五章基本内容示例(含答案)


对比，得 a = −5, b = −6, c = 6 （1 分）
3.
解：设 f (t) F(s), yzs (t) Y (s), g(t) G(s) ，可得
G(s) = 1 − 1 + 2 ，Y(s) = 1 − 2 + 3
s s+2 s+3
s +1 s + 2 s +3
又由 (t) 1 （1 分），因此 s
正确答案的序号填在括号内。）
1、指出下面哪个说法是正确的，__________。
A. 线性时不变系统零状态响应的象函数等于系统函数与激励的象函数的乘积。 B. 在零状态条件下，元件的 s 域模型中，描述动态元件（L、C）初始状态的内部象
电源全为零，这时网络的 s 域模型与原电路形式与电路参数都完全相同。
Z1 ( s )
=
1 sC1
•
(R2
+
1 sC2
12、______变换是分析线性连续系统的有力工具，它将描述系统的时域微积分 方程变换为 s 域的______方程，便于运算和求解。（____）
A、傅立叶、微分 C、积分、代数 E、拉氏、代数 G、代数、积分
B、代数、微分 D、傅立叶、差分 F、代数、代数 H、拉氏、积
13、已知两个子系统的系统函数分别为 H1(s), H2 (s) ，则由这两个子
）
A．
B．-10
C． -11
D．1
3．因果系统转移函数 H (s) 的零极图如下图所示，此系统属于（ ）系统。
A．临界稳定的
B．不稳定的
j
C．无法判断稳定性 D．稳定的
-1 -1/2 0
4. 单边拉氏变换象函数 F(s)的收敛坐标σ< 0，则其收敛坐标在虚轴以左，在 这种情况下，___________________________。（____） A、 F(s)式在虚轴上不收敛，因此不能直接计算其傅里叶变换 B、F(s)式中，令 s=jω，就得到相应的傅里叶变换 C、 F(s)式在虚轴上收敛，但也不能直接计算其傅里叶变换 D、函数 f(t)的傅里叶变换不存在

信号与系统第5章课后习题答案

5.5 离散信号()f n 的波形如习题图5-3所示，试画出下列信号的波形。

(2)(1)(4)(2)(6)(1)(1)(8)(1)()(10)(1)(1)f n f n f n f n f n U n f n U n - +×- -- ---+习题图5-3(2)(1)f n -(4)(2)f n32211()10(2)102100n n n f n n f n n n =-ìï =- 3 =-ìïïï= = Þ = =ííïï = îïï î其他其他+×-(6)(1)(1)f n f n--(8)(1)()f n U n---+f n U n(10)(1)(1)5.17 求下列差分方程所描述的系统的单位样值响应。

1(1)()(2)()9y n y n f n --=解：单位样值响应是指当激励信号为()n d 时系统的零状态响应。

要求单位样值响应，输入()()f n n d =，代入差分方程得：1()(2)()(1)9h n h n n d --= LLL在0n >时，()0n d =，有1()(2)09h n h n --= 特征方程为：2121110,933l l l -= Þ =- =1211()()((2)33n nh n C C \ =-+ LLL0()0(())n h n h n < = Q 时，；因为单位样值响应是零状态响应1()(2)()91(0)(2)(0)191(1)(1)(1)09h n h n n h h h h d d d =-+ \ = -+== -+=由(1)式得： 121122(0)(1)1(0)12111(1)(0332h h h C C C h C C C ì =+==üïïïÞ ýí = -+=ïï=þïî将、代入（2）式得：1111()[((]()2323n nh n U n \ =-+5.18 求习题图5-5所示系统的单位样值响应。

信号和系统第5章习题答案解析

第5章 连续时间信号的抽样与量化5.1 试证明时域抽样定理。

证明： 设抽样脉冲序列是一个周期性冲激序列，它可以表示为∑∞-∞=-=n sT nT t t )()(δδ由频域卷积定理得到抽样信号的频谱为：[])()(21)(ωδωπωT s F F *=()[]∑∞-∞=-=n ssn F T ωω1式中)(ωF 为原信号)(t f 的频谱，)(ωδT 为单位冲激序列)(t T δ的频谱。

可知抽样后信号的频谱)(ωs F 由)(ωF 以 s ω为周期进行周期延拓后再与s T 1相乘而得到，这意味着如果m s ωω2≥，抽样后的信号)(t f s 就包含了信号)(t f 的全部信息。

如果m s ωω2<，即抽样间隔ms f T 21>，则抽样后信号的频谱在相邻的周期内发生混叠，此时不可能无失真地重建原信号。

因此必须要求满足ms f T 21≤，)(t f 才能由)(t f s 完全恢复，这就证明了抽样定理。

5.2 确定下列信号的最低抽样频率和奈奎斯特间隔： （1）)50(t Sa（2）)100(2t Sa（3） )100()50(t Sa t Sa +（4）)60()100(2t Sa t Sa +解：抽样的最大间隔m s f T 21=称为奈奎斯特间隔，最低抽样速率m s f f 2=称为奈奎斯特速率，最低采样频率m s ωω2=称为奈奎斯特频率。

（1）)]50()50([50)50(--+↔ωωπu u t Sa ，由此知s rad m /50=ω，则π25=m f ，由抽样定理得：最低抽样频率π502==m s f f ，奈奎斯特间隔501π==s s f T 。

（2）)2001(100)100(2ωπ-↔t Sa脉宽为400，由此可得s rad m /200=ω，则π100=m f ，由抽样定理得最低抽样频率π2002==m s f f ，奈奎斯特间隔2001π==s s f T 。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
F ( s) = K1 K K + 2 + 3 s s+2 s+4
K1 =
( s + 1)( s + 3) 3 ×s = s ( s + 2)( s + 4) 8 s =0 ( s + 1)( s + 3) 1 = ( s + 2) s ( s + 2)( s + 4) 4 s = −2
K2 =
K3 =
1 1 F (s) = × s 1 − e− s
故 (3)
f (t ) = U (t ) ∗ ∑ δ (t − K ) = ∑ U (t − K )
n =0 k =0
∞
∞
,
K∈N
F (s) =
1 − e− s 1 − e− s × s 2
因有 故
1 U (t ) − U (t − 1) ↔ (1 − e − s ) s
(4)
F ( s) =
1 4 s2 3s + 2 =1− =1+ − 2 s + 3s + 2 ( s + 1)(s + 2) s +1 s + 2
f (t ) = δ (t ) + (e − t − 4e −2t )U (t )
5.3 求下列各像函数 F (s ) 的原函数 f (t ) 。
(1) F (s ) =
5.8 图题 5-8(a)所示电路，已知激励 f (t ) 的波形如图题 5-8(b)所示。求响 应 u (t ) ，并画出 u (t ) 的波形。
f (t ) / V
1Ω
N
3
+
f (t )
+
-
1Ω
1F
u (t )
0 -2
t
-
(a)
(b)
图题 5-8 答案 图题 5-8（a）所示电路的开关等效电路，如图题 5-8（c）所示。 t < 0 时 S 在 1，电路已
2
(2) F (s ) =
1 s (1 − e − s )
⎡1 − e − s ⎤ (3) F (s ) = ⎢ ⎥ ⎣ s ⎦
答案 (1)
F ( s) =
因
2 1 2e − ( s −1) + × ( s − 1) 2 + 22 2 ( s − 1) 2 + 22
又因有
sin 2tU (t ) ↔
s 3 + 6s 2 + 6s s 2 + 6s + 8
(2) F (s ) =
1 2 s (s + 1)
2
答案 (1)
F (s) = s + 2 −4 + s+2 s+4
f (t ) = δ ′(t ) + (2e −2t − 4e −4t )U (t )
(2)
F (s) =
K11 K12 K K 21 K 22 1 2 3 1 −3 + + 13 + 2 + = + + + 2+ 3 2 3 2 ( s + 1) ( s + 1) s +1 s s ( s + 1) ( s + 2) s +1 s s
答案
2 令 F ( s ) 的分母 ( s + 2) ( s + 3) = 0 ，得到一个单极点 s1 = −3 和一个二重极点
s2 = −2 。下面求各
极点上的留数。
Re s1 = F ( s )(s + 3)e st
[
]
s = −3
⎡ 4s 2 + 17 s + 16 st ⎤ e ⎥ = e − 3t =⎢ 2 ⎣ ( s + 2) ⎦ s = −3
s2 + 2s + 1 s3 − s2 − s + 1
(2) F (s ) =
s3 s2 + s + 1
(3) F (s ) =
2s + 1 3 s + 3s 2 + 2 s
(4) F (s ) =
1 − e −2 s s (s 2 + 4 )
答案 （1） 初值定理应用的条件是， F ( s ) 必须是真分式；终值定理应用的条件式：
2 s +4
2
故由时移性有 又由复频移性有
sin 2(t − 1)U (t − 1) ↔
2 e −s s  (t − 1) ↔
2 e − ( s −1) 2 ( s − 1) + 4
故 (2)
1 f (t ) = et sin 2tU (t ) + et sin 2(t − 1)U (t − 1) 2
1 s + s +1
2
又
F (s) = s − 1 +
故
f (0 + ) = lim s
s→∞
1 =0 s + s +1
2
(3)
f (∞ ) = lim s
s →0
2s + 1 1 = 3 s + 3s + 2 s 2
3
f (0 + ) = lim s
s →∞
2s + 1 =0 s + 3s 2 + 2 s
F ( s ) 的极点必
须在 s 平面的左半开平面；（2）在 s = 0 处， F ( s ) 只能有一阶极点。也就是 说，终值定理只 有在 f (t ) 有终值的情况下才能应用。例如，当 f (t ) 维周期函数时就，终值定 理就不能适用了。 (1)
F ( s) =
s 2 + 2s + 1 ( s + 1) 2 ( s + 1) 2 = = s 3 − s 2 − s + 1 ( s − 1)( s 2 − 1) ( s − 1) 2 ( s + 1)
f (t ) = ( 12 − 2t 34 − 3t 152 −12t e − e + e )U (t ) 5 9 45
(3) 3s + 5 2 1 =2+ + ( s + 1)( s + 2) s +1 s + 2
F ( s) = 2 +
f (t ) = 2δ (t ) + (2e − t + e −2t )U (t )
3e − 2t + (−2)te − 2t = (3 − 2t )e − 2t
[
]
故
f (t ) = e −3t + (3 − 2t )e −2t U (t )
[
]
+ 5.6 求下列各像函数 F (s ) 的原函数 f (t ) 的初值 f (0 ) 与终值 f (∞ ) 。
(1) F (s ) =
(s + 1)(s + 3) s (s + 2 )(s + 4 )
2s2 + 9s + 9 s 2 + 3s + 2
(2) F (s ) =
2 s 2 + 16 (s 2 + 5s + 6)(s + 12 )
(3) F (s ) =
(4) F (s ) =
s3 (s 2 + 3s + 2)s
答案 (1)
3
(4)
f (0 + ) = lim s
s →∞
1 − e −2 s =0 s( s 2 + 4)
因 F ( s ) 在 jω 轴上有一对共轭极点，故 F ( s ) 对应的 f (t ) 不存在终值。
'' ' ' 5.7 已知系统的微分方程为 y (t ) + 3 y (t ) + 2 y (t ) = f (t ) + 3 f (t )
第五章 习 题
5.1 求下列各时间函数 f (t ) 的像函数 F (s ) 。
− at (1) f (t ) = (1 − e )U (t )
(2) f (t ) = sin (ωt + φ )U (t )
1 1 − e − at U (t ) a
(3) f (t ) = e
− at
(1 − at )U (t )
f (t ) = [U (t ) − U (t − 1)] ∗ [U (t ) − U (t − 1)] = tU (t ) − 2(t − 1)U (t − 1) + (t − 2)U (t − 2)
5.5 用留数法求像函数 F (s ) =
4 s 2 + 17 s + 16 的原函数 f (t ) 。 2 (s + 2 ) (s + 3)
(8)
−α t F ( s ) = L [ e + α t − 1] = L ⎡ ⎣ − (1 − e ) ⎤ ⎦ + L [α t ] =
−α α α2 + 2 = 2 s(s + α ) s s (s + α )
5.2 求下列各像函数 F (s ) 的原函数 f (t ) 。
(1) F (s ) =
(2)
F (s) =
s sinψ + ω cosψ s2 + ω
F ( s) =
(3)
s (s + α )2
F ( s) =
(4)
1
α
×
α
s(s + α )
=
1 s( s + α )