运算律》知识点归纳及练习

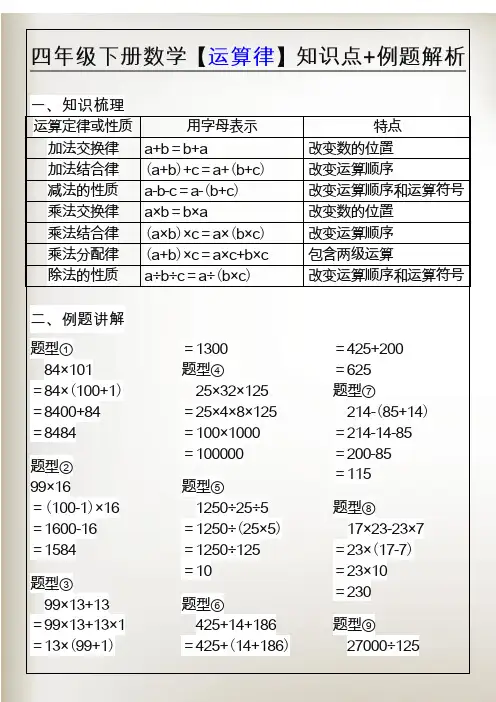
四年级下册数学【运算律】知识点+例题解析一、知识梳理运算定律或性质用字母表示特点加法交换律a+b＝b+a 改变数的位置加法结合律(a+b)+c＝a+(b+c)改变运算顺序减法的性质a-b-c＝a-(b+c)改变运算顺序和运算符号乘法交换律a×b＝b×a 改变数的位置乘法结合律(a×b)×c＝a×(b×c)改变运算顺序乘法分配律(a+b)×c＝a×c+b×c 包含两级运算除法的性质a÷b÷c＝a÷(b×c)改变运算顺序和运算符号二、例题讲解题型①84×101＝84×(100+1)＝8400+84＝8484题型②99×16＝(100-1)×16 ＝1600-16＝1584题型③99×13+13 ＝99×13+13×1 ＝13×(99+1)＝1300题型④25×32×125＝25×4×8×125＝100×1000＝100000题型⑤1250÷25÷5＝1250÷(25×5)＝1250÷125＝10题型⑥425+14+186＝425+(14+186)＝425+200＝625题型⑦214-(85+14)＝214-14-85＝200-85＝115题型⑧17×23-23×7＝23×(17-7)＝23×10＝230题型⑨27000÷125＝27×1000÷125 ＝27×8 ＝216四年级下册数学【运算律】知识点+例题解析一、知识梳理运算定律或性质用字母表示特点加法交换律a+b＝b+a 改变数的位置加法结合律(a+b)+c＝a+(b+c)改变运算顺序减法的性质a-b-c＝a-(b+c)改变运算顺序和运算符号乘法交换律a×b＝b×a 改变数的位置乘法结合律(a×b)×c＝a×(b×c)改变运算顺序乘法分配律(a+b)×c＝a×c+b×c 包含两级运算除法的性质a÷b÷c＝a÷(b×c)改变运算顺序和运算符号二、例题讲解题型①84×101＝84×(100+1)＝8400+84＝8484题型②99×16＝(100-1)×16 ＝1600-16＝1584题型③99×13+13 ＝99×13+13×1 ＝13×(99+1)＝1300题型④25×32×125＝25×4×8×125＝100×1000＝100000题型⑤1250÷25÷5＝1250÷(25×5)＝1250÷125＝10题型⑥425+14+186＝425+(14+186)＝425+200＝625题型⑦214-(85+14)＝214-14-85＝200-85＝115题型⑧17×23-23×7＝23×(17-7)＝23×10。

运算定律与简便计算（一）加减法运算定律1.加法交换律定义：两个加数交换位置，和不变字母表示：a b b a +=+例如：16+23=23+16 546+78=78+5462.加法结合律定义：先把前两个数相加，或者先把后两个数相加，和不变。

字母表示：)()(c b a c b a ++=++注意：加法结合律有着广泛的应用，如果其中有两个加数的和刚好是整十、整百、整千的话，那么就可以利用加法交换律将原式中的加数进行调换位置，再将这两个加数结合起来先运算。

例1.用简便方法计算下式：（1）63+16+84 （2）76+15+24 （3）140+639+860举一反三：（1）46+67+54 （2）680+485+120 （3）155+657+2453.减法交换律、结合律注：减法交换律、结合律是由加法交换律和结合律衍生出来的。

减法交换律：如果一个数连续减去两个数，那么后面两个减数的位置可以互换。

字母表示：b c a c b a --=--例2.简便计算：198-75-98减法结合律：如果一个数连续减去两个数，那么相当于从这个数当中减去后面两个数的和。

字母表示：)(c b a c b a +-=--例3.简便计算：（1）369-45-155 （2）896-580-1204.拆分、凑整法简便计算拆分法：当一个数比整百、整千稍微大一些的时候，我们可以把这个数拆分成整百、整千与一个较小数的和，然后利用加减法的交换、结合律进行简便计算。

例如：103=100+3，1006=1000+6，…凑整法：当一个数比整百、整千稍微小一些的时候，我们可以把这个数写成一个整百、整千的数减去一个较小的数的形式，然后利用加减法的运算定律进行简便计算。

例如：97=100-3，998=1000-2，…注意：拆分凑整法在加、减法中的简便不是很明显，但和乘除法的运算定律结合起来就具有很大的简便了。

例4.计算下式，能简便的进行简便计算：（1）89+106 （2）56+98 （3）658+997随堂练习：计算下式，怎么简便怎么计算（1）730+895+170 （2）820-456+280 （3）900-456-244（4）89+997 （5）103-60 （6）458+996（7）876-580+220 （8）997+840+260 （9）956—197-56（二）乘除法运算定律1.乘法交换律定义：交换两个因数的位置，积不变。

四年级下册运算律知识点归纳
加法运算律。

1. 加法交换律：两个加数相加，交换加数的位置，和不变。

用字母表示为：a + b = b + a
2. 加法结合律：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。

用字母表示为：(a + b) + c = a + (b + c)
乘法运算律。

1. 乘法交换律：两个因数相乘，交换因数的位置，积不变。

用字母表示为：a × b = b × a
2. 乘法结合律：三个数相乘，先乘前两个数，或者先乘后两个数，积不变。

用字母表示为：(a × b) × c = a × (b × c)
3. 乘法分配律：两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加。

用字母表示为：(a + b)×c = a×c + b×c
简便运算。

在进行简便运算时，要根据运算律，对算式进行变形，使计算更加简便。

例如：。

1. 25 + 36 + 75 = (25 + 75) + 36 = 100 + 36 = 136（运用了加法交换律和结合律）。

2. 25×4×8 = (25×4)×8 = 100×8 = 800（运用了乘法结合律）。

3. 102×56 = (100 + 2)×56 = 100×56 + 2×56 = 5600 + 112 = 5712（运用了乘法分配律）。

苏教版四年级数学下运算律知识点（内部资料）知识点一：加法交换律和结合律1．加法交换律：两个数相加，交换加数的位置，和不变。

用字母表示为：a+b=b+a 2．加法结合律：三个数相加，先把前两个数相加，再和第三个数相加，或者先把后两个数相加，再和第一个数相加，和不变。

用字母表示为：（a+b）+c=a+（b+c）。

例1.1 ：填上适当的数。

81+（）= 62 + 81 184 + 168 + 32 = 184+ （+ 32 ）练习1.2 ：选出正确答案，将序号填在相应的括号里。

①41+37+13=41+（37+13）②x+y=y+x ③ 35+（b+65）=（35+65）+b ④ a+b+c=a+c+b ⑤32+45+55=32+（45+55）⑥m+n+t=n+（m+t）只应用加法交换律的是（）。

只应用加法结合律的是（）。

既应用加法交换律，又应用加法结合律的是（）。

知识点二：应用加法运算律进行简便计算在连加计算中，当某些加数相加可以凑成整十、整百、整千的数时，运用加法运算律可使计算简便。

口诀：连加计算仔细看，考虑加数是关键。

整十、整百与整千，结合起来更简单。

交换定律记心间，交换位置和不变。

结合定律应用广，加数凑整更简便。

例2.1 ：69+75+25 78+（47+22）387+98（多加要减）387+10（2 少加要加）387﹣98（多减要加）387﹣102（少减要减）练习2.2 ：99+124+201 380+345+120 9321+4523+972+679+5477+28苏教版四年级数学下运算律知识点（内部资料）知识点三：减法的运算性质1：一个数连续减去两个数等于这个数减去这两个减数的和。

用字母表示：a-b-c=a-（b+c）减法的运算性质2：一个数减去两个数的和等于这个数连续减去和里每个加数。

例3.1 ：324-58-42 670-25-75159﹣（59+37）268 ﹣（35+68）加减的规律：（1）先加后减等于先减后加。

第三单元运算律整理知识点一、知识概述《运算律》①基本定义：运算律就是在进行四则运算（加、减、乘、除）的时候，一些能让计算变得简便的规律。

比如说加法交换律，就是两个数相加，交换它们的位置，和不变。

像3 + 5 = 5 + 3。

乘法分配律呢，就是一个数乘两个数的和，可以分别乘这两个数，再把积相加，比如3×（2 + 4）=3×2+3×4。

②重要程度：在数学学科里那可是非常重要的。

就像盖房子的基石一样，从简单的四则运算到复杂的代数运算，到处都有它的身影。

要是不懂运算律，做数学题的时候就会绕很多弯路，复杂的计算可能就没法做下去了。

③前置知识：得先掌握基本的四则运算，知道什么是加法、减法、乘法和除法，还有正数、负数等这些基础的数的概念。

比如说你得知道2 + 3是多少，5 - 1是多少这样的基础计算。

④应用价值：在生活中也经常能用到。

比如说去超市买东西，有促销活动的时候，你得计算不同组合的商品价格是不是划算，这就可能用到运算律。

或者计算家庭每月收支的时候，把收入和支出分类计算，其实也是在不知不觉中用运算律简化计算。

二、知识体系①知识图谱：运算律在小学数学学科里就是四则运算这个大板块中的核心规则部分。

它就像一张网中的节点，联系着各个不同运算类型之间的关系。

②关联知识：和整数、小数、分数的运算都有联系。

比如说整数的加法交换律，在小数、分数的加法里同样适用。

而且和后面要学的方程运算也密切相关，解方程很多步骤就是依据运算律来简化的。

③重难点分析：掌握难度中等偏上吧。

难点就是区分不同运算律之间的差别，像乘法结合律和乘法分配律就很容易弄混。

关键点在于理解每个运算律的本质含义，会根据具体的算式去选择合适的运算律来简化。

④考点分析：在考试中那可太重要了。

既会单独出题考查运算律的概念，像问加法交换律是什么；也会在四则混合运算的大题里考查运算律的运用，看是否能正确运用运算律简便计算。

三、详细讲解【理论概念类】①概念辨析：加法交换律：两个数相加，交换加数的位置，和不变。

有理数的运算知识点汇总及练习有理数的运算知识点汇总：一、有理数的加减法有理数加法法则：1.同号两数相加，取相同的符号，并把绝对值相加；2.异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值；3.一个数与相加，仍得这个数.有理数加法运算律：1.加法的交换律：a+b=b+a；2.加法的结合律：（a+b）+c=a+（b+c）.在运用运算律时，可以灵活运用以下规律：1）互为相反数的两个数先相加——“相反数结合法”；2）符号相同的两个数先相加——“同号结合法”；3）分母相同的数先相加——“同分母结合法”；4）几个数相加得到整数，先相加——“凑整法”；5）整数与整数、小数与小数相加——“同形结合法”。

有理数减法法则：减去一个数，等于加上这个数的相反数；即a-b=a+（-b）.二、有理数的乘除法有理数乘法法则：1.两数相乘，同号得正，异号得负，并把绝对值相乘；2.任何数同0相乘，都得0；3.几个不是0的数相乘，负因数的个数是偶数时，积是正数；负因数的个数是奇数时，积是负数；4.几个数相乘，如果其中有因数为0，则积等于0.有理数乘法的运算律：1）乘法的交换律：ab=ba；2）乘法的结合律：（ab）c=a（bc）；3）乘法的分配律：a（b+c）=ab+ac。

有理数除法法则：1.除以一个不等于0的数，等于乘以这个数的倒数。

2.两数相除，同号得正，异号得负，并把绝对值相除。

三、有理数的加减乘除混合运算乘除混合运算往往先将除法化成乘法，然后确定积的符号，最后求出结果。

有理数加减乘除混合运算，如果有括号先计算括号里的，如果无括则按照‘先乘除，后加减’的顺序进行。

知识点3：有理数乘方乘方的概念：求n个相同因数的积的运算，叫做乘方，乘方的结果叫做幂。

乘方中，相同的因式叫做底数，相同因式的个数叫做指数。

记作an，在an中，a叫做底数，n叫做指数。

乘方的性质：1）负数的奇次幂是负数，负数的偶次幂的正数。

2）正数的任何次幂都是正数，0的任何正整数次幂都是0.练10：混合运算中的简便运算技巧1.计算：15\div\frac{5}{1}-\frac{51\times(-1/2)}{\frac{7}{-7} -\frac{8}{-27}}$$化XXX：15\times\frac{1}{5}-\frac{51}{2}\div\frac{7}{-7+8/27}$$继续化简得：3- \frac{51}{2}\div\frac{7\times27-8}{27}$$最终结果为：frac{249}{22}$$2.某个家庭为了估计自己家6月份的用电量，对月初的一周每天电表的读数进行了记录，上周日电表的读数是115度．以后每日的读数如下表(表中单位：度)，请你估计6月份大约用多少度电．星期。

有理数的运算知识点汇总知识点1:有理数的加减法一、有理数加法法则：1.同号两数相加，取相同的符号，并把绝对值相加；2.异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值；3.一个数与0相加，仍得这个数.二、有理数加法运算律：1.加法的交换律：a+b=b+a；2.加法的结合律：（a+b）+c=a+（b+c）.3.在运用运算律时，一定要根据需要灵活运用，以达到化简的目的，通常有下列规律：（1）互为相反数的两个数先相加——“相反数结合法”；（2）符号相同的两个数先相加——“同号结合法”；（3）分母相同的数先相加——“同分母结合法”；（4）几个数相加得到整数，先相加——“凑整法”；（5）整数与整数、小数与小数相加——“同形结合法”。

三、有理数减法法则：减去一个数，等于加上这个数的相反数；即a-b=a+（-b）.知识点2：有理数的乘除法一、有理数乘法：1.有理数乘法法则法则一：两数相乘，同号得正，异号得负，并把绝对值相乘；（“同号得正，异号得负”专指“两数相乘”的情况，如果因数超过两个，就必须运用法则三）法则二：任何数同0相乘，都得0；法则三：几个不是0的数相乘，负因数的个数是偶数时，积是正数；负因数的个数是奇数时，积是负数；法则四：几个数相乘，如果其中有因数为0,则积等于0.2.有理数乘法的运算律：（1）乘法的交换律：ab=ba；（2）乘法的结合律：（ab）c=a（bc）；（3）乘法的分配律：a（b+c）=ab+ac .二、有理数除法法则1.除以一个不等0的数，等于乘以这个数的倒数。

2.两数相除，同号得正，异号得负，并把绝对值相除。

0除以任何一个不等于0的数，都得0三.有理数的加减乘除混合运算1.乘除混合运算往往先将除法化成乘法，然后确定积的符号，最后求出结果。

2.有理数加减乘除混合运算，如果有括号先计算括号里的，如果无括则按照‘先乘除，后加减’的顺序进行。

知识点3：有理数乘方一、乘方1.乘方的概念（1）求n 个相同因数的积的运算，叫做乘方，乘方的结果叫做幂。

律
用字母表示数,渗透了符号化思想。

符号化思想就是用符号化的语言(包括字母、数字、图形和各种特定的符号)来描述数学的内容。

举例:用简便算法计算29+16+24,3个数连加,运用加法结合律可以简便运算。

16+24正好是40,先算比较简便。

29+16+24
=29+(16+24)
=29+40
=69
在应用加法运算律进行简算时,有时会同时用到两种运算律。

易错点:加法交换律和乘法交换律改变的是加数和乘数的位置,结果不变。

在应用乘法运算律简算时,有时会同时用到两种或两种以上的运算律。

要点提示:加法结合律和乘法结合律改变的是运算顺。

第四单元运算律知识点一：买文具-四则混合运算顺序（1）四则混合运算顺序在没有括号的算式里，当只有加、减运算或乘、除运算时，按从左到右的顺序进行计算，既有加、减运算，又有乘、除运算时，要先算，再算。

（2）含有中括号的四则混合运算在一个算式里，如果既有小括号又有中括号，要先算的，再算面的，最后算。

知识点二：运算律及其应用加法交换律用字母表示为 a＋b＝加法结合律用字母表示为（a+b）+c=乘法交换律用字母表示为 a×b＝乘法结合律用字母表示为 (a×b) ×c=乘法分配律用字母表示为 (a+b) ×c=1.在连加计算中，运用可以让一些加法计算简便。

2.乘法结合律只适用于运算，不可以在乘加或乘减运算中运用。

3.乘法分配律可以正用，也可以逆用。

如果a×c和b×c计算简便时，可以先算a×c和b×c，再把两个积相加；如果a＋b的和正好是整十、整百、整千数时，可以用来计算。

4.运用乘法分配律进行计算时，两个加数要，然后再把。

【易错典例1】（2019秋•嘉陵区期末）实践探究．【思路引导】根据整数乘法的竖式计算法则解答即可．【完整解答】解：乘数14个位上的4与326相乘，表示4×326的积是1304，十位上的1与326相乘，表示10×326的积是3260；【易错注意点】此题考查了整数乘法的竖式计算方法．【易错典例2】（2019秋•洛川县期末）如图算式中的汉字各代表什么数字？我＝3；是＝9；中＝7；国＝1；人＝0．【思路引导】根据整数乘法的运算法则，第一个因数与第二个因数的个位相乘得：3438，所以第二个因数的个位为9，第一个因数的百位为3．原式为：382×29＝11078，完成竖式，并找到各汉字代表的数字．【完整解答】解：原式为：所以：我＝3；是＝9；中＝7；国＝1；人＝0．故答案为：3；9；7；1；0．【易错注意点】本题主要考查凑数谜，关键根据整数乘法及加法的运算法则，找到合适的数，完成计算．【易错典例3】点A表示的数可能是算式（）的积．A．201×51B．199×45C．199×51【思路引导】根据题意，点A介于1与10000之间，且更接近10000；根据估算的计算方法，分别求出各个算式的结果，再进一步解答．【完整解答】解：201×51≈200×50＝10000，等于10000，不符合题意；199×45≈200×45＝9000，接近10000，符合题意；199×51≈200×50＝10000，等于10000，不符合题意；故选：B．【易错注意点】考查了三位数乘两位数的估算，把两位数看作与它接近的整十整百数，然后再进一步解答．【易错典例4】（2018秋•单县期末）学校准备发练习本，发给15个班，每班144本，还要留40本作为备用．学校应买多少练习本？【思路引导】首先用发给每个班的练习本的数量乘班级的数量，求出发给15个班多少本练习本；然后用它加上备用的练习本的数量，求出学校应买多少练习本即可．【完整解答】解：144×15+40＝2160+40＝2200（本）答：学校应买2200本练习本．【易错注意点】此题主要考查了整数乘法的意义和应用，要熟练掌握，解答此题的关键是求出发给15个班多少本练习本．:考点1：带括号的混合运算（含较大数的除法）1．（2020春•江北区期末）把方框中的三个分步算式合并成综合算式是（）12+6＝1836÷18＝220+2＝22A．36÷（12+6）+20B．20+36÷（12+6）C．36÷12+6+20D．36÷（12+6）+22．（270+770÷55）﹣190÷10正确的运算顺序是（）A．②除法→①加法→③减法→④除法B．②除法→①加法→③减法→②除法C．②除法→①加法→④除法→③减法3．（2021春•浑源县期中）用计算器计算（801﹣576）÷15时，当按到“÷”的时候，显示屏上显示接着按“15”，再按“＝”，显示屏上显示的是。

《运算律》知识点归纳及练习乘法结合律1、乘法结合律：三个数相乘,先把前两个数相乘,再和第三个数相乘,或者先把后两个数相乘,再和第一个数相乘,它们的积不变。

用字母表示是：（a×b）×c=a×(b×c).使用时机：当几个数相乘时,如果其中两个数相乘得整十、整百、整千的数就可以应用乘法交换律和乘法结合律。

乘法结合律可以改变乘法运算中的顺序。

数字如;25和4、50和2、125和8、50和4、500和2等。

加法运算时也有结合律。

如果用a/b/c表示三个数,那么加法结合律表示为：（a+b）+c=a+（b+c）2、认识乘法交换律两个数相乘,交换他们的位置,积不变,这叫乘法交换律。

如用字母a、b表示两个数,那么乘法交换律用字母表示为：a×b=b×a。

1）上述规律可推广到更多个数相乘。

如：125×4×8×25=（125×8）×（25×4）=1000×100=1000002）加法运算时也有交换律,如用字母a、b表示两个数,那么加法交换律用字母表示为：a+b=b+a。

3）运用加法交换律和结合律可以使得一些运算简便。

50+7+40+9=（50+40）+（7+9）=90+16=106练习题：73×25×4 125×63×8 4×（25×93） 12×125×5×832×125×25 48×125×5乘法分配律1、乘法分配律：两个数的和（或差）与一个数相乘,可以把两个加数（或被减数、减数）分别与这个数相乘,在把两个积相加（或相减）,结果不变。

用字母表示数：（a+b）×c=a×c+b×c或（a-b）×c=a×c－b×c1、式子的特点：式子的运算符号一般是×、+(-)、×的形式；在两个乘法式子中,有一个相同的因数；另为两个不同的因数之和(或之差)是能凑成整十、整百、整千的数。