单筋T形截面梁抗弯承载力自动计算表

钢筋混凝土T形梁桥主梁设计资料⒈某公路钢筋混凝土简支梁桥主梁结构尺寸。

标准跨径：20.00m；计算跨径：19.50m；主梁全长：19.96m；梁的截面尺寸如下图（单位mm）：⒉计算内力⑴使用阶段的内力跨中截面计算弯矩(标准值)结构重力弯矩：M1/2恒＝759.45kN－m；汽车荷载弯矩：M1/2汽＝697.28kN－m(未计入冲击系数)；人群荷载弯矩：M1/2人＝55.30kN－m；1/4跨截面计算弯矩（设计值）M d,1/4＝1687kN－m；（已考虑荷载安全系数）支点截面弯矩M d0=0，支点截面计算剪力(标准值)结构重力剪力：V0恒＝139.75kN；汽车荷载剪力：V0汽＝142.80kN(未计入冲击系数)；人群荷载剪力：V0人＝11.33kN；跨中截面计算剪力（设计值）跨中设计剪力：V d=84kN（已考虑荷载安全系数）；，1/2主梁使用阶段处于一般大气条件的环境中。

结构安全等级为二级。

汽车冲击系数，汽车冲击系数1+μ＝1.292。

⑵施工阶段的内力简支梁在吊装时，其吊点设在距梁端a=400mm处，而梁自重在跨中截面的弯矩标准值M k=505.69kN—m，吊点的剪力标准值V0=105.57kN。

，1/2⒊材料主筋用HRB335级钢筋f sd＝280N/mm2；f sk＝335N/mm2；E s＝2.0×105N/mm2。

箍筋用R235级钢筋f sd＝195N/mm2；f sk＝235N/mm2；E s＝2.1×105N/mm2。

采用焊接平面钢筋骨架混凝土为30号f cd＝13.8N/mm2；f ck＝20.1N/mm2；f td＝1.39N/mm2；f tk＝2.01N/mm2；E c＝3.00×104N/mm2。

作用效应组合主梁正截面承载力计算主梁斜截面承载力计算全梁承载力校核施工阶段的应力验算使用阶段裂缝宽度和变形验算纵向构造钢筋、架立钢筋及骨架构造钢筋长度计算钢筋明细表及钢筋总表第1章 作用效应组合§1.1 承载力极限状态计算时作用效应组合 根据《公路桥涵设计通用规范》（JTG D60—2004）4·1·6条规定：按承载力极限状态计算时采用的基本组合为永久作用的设计值效应与可变作用设计值效应相组合，其效应组合表达式为：)(211100∑∑==++=nj QjK Qj C K Q Q m i GiK Gi ud S S S S γψγγγγ跨中截面设计弯矩M d =γG M 恒+γq M 汽+γq M 人=1.2×759.45+1.4×1.292×697.28+1.4×55.30=2250.00kN －m 支点截面设计剪力V d =γG V 恒+γG1V 汽+γG2V 人=1.2×142.80+1.4×1.292×139.75+1.4×11.33=440.00kN §1.2 正常使用极限状态设计时作用效应组合 根据《公路桥涵设计通用规范》（JTG D60—2004）4·1·7条规定：公路桥涵结 构按正常使用极限状态设计时，应根据不同的设计要求，分别采用不同效应组合 ⑴作用效应短期组合作用效应短期组合为永久作用标准值效应与可变作用频遇值效应相组合，其效应 组合表达式为：∑∑==+=nj Qjk j mi Gik sd S S S 111ψM sd =M gk +ψ11M 11+ψ12M 12=759.45+0.7×697.28+1.0×55.30=1302.85kN －m ⑵作用长期效应组合作用长期效应组合为永久作用标准值效应与可变作用准永久值效应相组合，其效应组合表达式为：∑∑==+=nj Qjk j mi Gik ld S S S 1211ψM ld =M gk +ψ21M 11+ψ22M 12=759.45+0.4×697.28+0.4×55.30=1060.48kN －m第2章 主梁正截面承载力计算§2.1 配筋计算⑴翼缘板的计算宽度b ′f根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62—2004）第4·2·2条规定：T 形截面受弯构件位于受压区的翼缘计算宽度，应按下列三者中最小值取用。

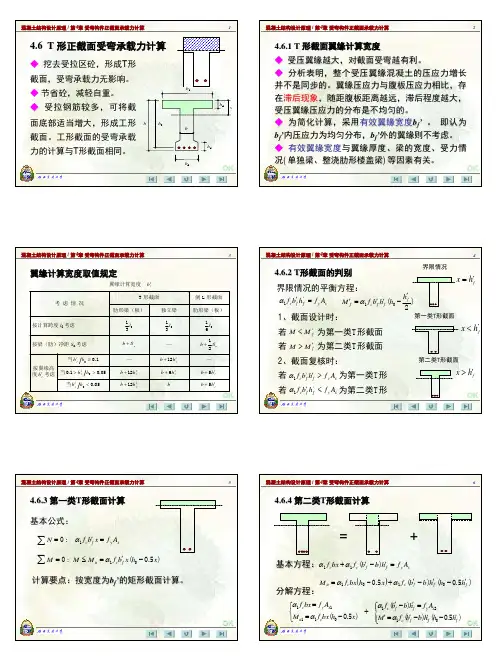
基本构件计算：单筋矩形梁正截面承载力计算一、计算简图二、基本公式1．公式法的三个基本公式：单筋矩形梁正截面受弯承载力计算的三个基本公式：s y c A f bx f =1α⎪⎭⎫ ⎝⎛-=≤201x h bx f M M c u α⎪⎭⎫ ⎝⎛-=≤20x h A f M M s y u式中 M —— 弯矩设计值；M u —— 受弯承载力设计值，即破坏弯矩设计值；c f 1α—— 混凝土等效矩形应力图的应力值； y f —— 钢筋抗拉强度设计值； s A —— 受拉钢筋截面面积； b —— 梁截面宽度； x —— 混凝土受压区高度；h 0 —— 截面有效高度，即截面受压边缘到受拉钢筋合力点的距离，h 0=h-a ； a —— 受拉钢筋合力点到梁受拉边缘的距离，当受拉钢筋为一排时，a =c+d/2； c —— 混凝土保护层厚度； d —— 受拉钢筋直径。

2．系数法的基本公式（1）系数的公式).(s ξ-ξ=α501(4-21)s αξ211--= (4-25)ξ-=α-+=γ5012211.ss (4-26)（2）基本公式 21201)5.01(bh f bh f M c s c ααξξα=-=0h A f M s s y γ=三、基本公式的适用条件1）防止超筋破坏b ξξ≤ 或 b ρρ≤ 或 0h x b ξ≤2）防止少筋破坏bh A A s s min min ,ρ=≥四、计算方法1．截面选择（设计题）按已知的荷载设计值作用下的弯矩M 设计截面时，常遇到下列两种情形： 情形1 ： 已知：M 、混凝土强度等级及钢筋等级；构件截面尺寸b 及h 。

求：所需的受拉钢筋截面面积A s 。

[解]（1）确定基本数据c f ；y f ；a h h -=0（2）计算有关系数21bh f Mc s αα=s αξ211--=ξ-=α-+=γ5012211.ss（3）计算受拉钢筋 0h f MA s y s γ=或 01bh f f A ycs αξ=（4）根据求得的受拉钢筋A s ，按照有关构造要求从附表20中选用钢筋直径和根数 （5）验算适用条件1）适用条件：b ξ≤ξ；2）若b ξ>ξ：需加大截面，或提高混凝土强度等级，或改用双筋矩形截面 3）验算bh A A m in m in ,s s ρ=≥。

T形截面受弯构件正截面承载力计算首先，我们需要确定T形截面的几何形状参数。

T形截面由两个部分组成，一部分是腿部，另一部分是横梁。

我们需要测量腿部和横梁的宽度b和高度h，以及腿部和横梁的厚度t1和t2接下来，我们需要确定材料的特性参数。

材料的特性参数包括弹性模量E和抗弯强度fy。

弹性模量表示材料在受应力作用下产生的变形程度，抗弯强度表示材料在受弯应力作用下的最大承载能力。

然后，我们需要确定加载方式。

T形截面受弯构件可以分为两种加载方式：一种是在腿部施加荷载，另一种是在横梁施加荷载。

对于腿部受载的情况，我们可以先假设T形截面的两个腿部均受到均匀荷载q的影响。

然后利用梁的理论计算方法，根据T形截面的几何形状和材料特性，计算出腿部的正截面承载力。

根据梁的理论计算方法，腿部受均匀荷载q的最大弯矩应为最大正截面弯矩M。

根据梁的力学方程M=E·I/y，其中E为弹性模量，I为截面的惯性矩，y为截面上其中一点的距离截面重心的垂直距离。

梁的截面惯性矩I可以根据截面几何形状的性质计算得到。

腿部的正截面承载力可以根据下式计算：P = fy·A = fy·(h1·t1 + h2·t2)其中，fy为材料的抗弯强度，A为截面的面积，h1和h2为腿部的高度，t1和t2为腿部的厚度。

最后，我们还需要根据截面几何形状的性质计算出腿部的扭转常数J和抗扭矩Wt。

扭转常数J表示截面抵抗扭转变形的能力，抗扭矩Wt表示截面的最大承载能力。

通过计算这两个参数，我们可以得到T形截面的抗扭矩Wt。

综上所述，我们可以通过测量T形截面的几何形状参数，确定材料的特性参数，采用梁的理论计算方法，计算出T形截面受弯构件的正截面承载力。

这将有助于工程师评估T形截面受弯构件的结构安全性，并进行合理的设计和优化。

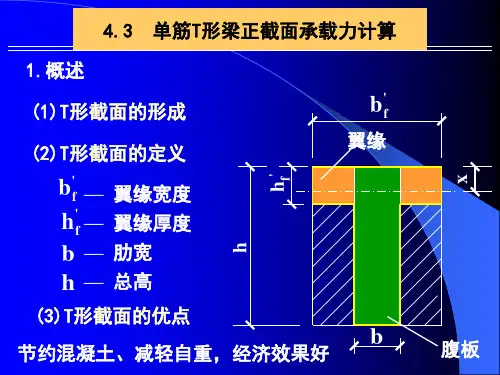
T形截面梁的计算首先，我们需要知道T形截面梁的几何形状参数，包括底部宽度b、顶部宽度bf、腹板厚度tf、翼缘宽度tw和翼缘厚度tf。

这些参数可以根据实际情况确定。

根据梁的受力情况，我们可以先计算出梁的截面模量W，用来描述梁的截面抗弯刚度。

根据梁的几何形状，T形截面梁的截面模量可以分为两个部分：腹板和翼缘。

腹板的截面模量Wf可以根据以下公式计算：Wf = (1/6) * tf * b^2翼缘的截面模量Wt可以根据以下公式计算：Wt = (1/2) * tw * (bf - tw) * (b + tf)梁的总截面模量W等于腹板截面模量Wf加上翼缘截面模量Wt：W=Wf+Wt接下来，根据梁的受力情况和截面模量W，可以计算梁的最大弯矩Mmax。

根据梁的几何形状，T形截面梁的最大弯矩可以分成三个部分：腹板、底部翼缘和顶部翼缘。

腹板的最大弯矩Mf可以根据以下公式计算：Mf=(1/2)*Wf*σy底部翼缘的最大弯矩Mt1可以根据以下公式计算：Mt1=Wt*(b/2)*σy顶部翼缘的最大弯矩Mt2可以根据以下公式计算：Mt2 = Wt * (b + tf - bf/2) * σy梁的最大弯矩Mmax等于腹板最大弯矩Mf加上底部翼缘最大弯矩Mt1和顶部翼缘最大弯矩Mt2：Mmax = Mf + Mt1 + Mt2根据梁的最大弯矩Mmax和截面模量W，可以计算梁的抗弯承载力。

抗弯承载力是指梁在承受弯曲作用下的最大承载能力。

梁的抗弯承载力可以根据以下公式计算：P = Mmax / σb其中，P为梁的抗弯承载力，Mmax为梁的最大弯矩，σb为材料的抗弯应力。

另外，需要注意的是，在计算过程中还需要考虑梁的剪力和剪切承载力。

剪力是指梁在受力作用下发生剪切变形的力，剪切承载力则是指梁在承受剪切力作用下的最大承载能力。

可以根据梁的几何形状和材料的抗剪强度计算剪力和剪切承载力。

综上所述，T形截面梁的计算方法主要包括计算截面模量、最大弯矩和抗弯承载力。

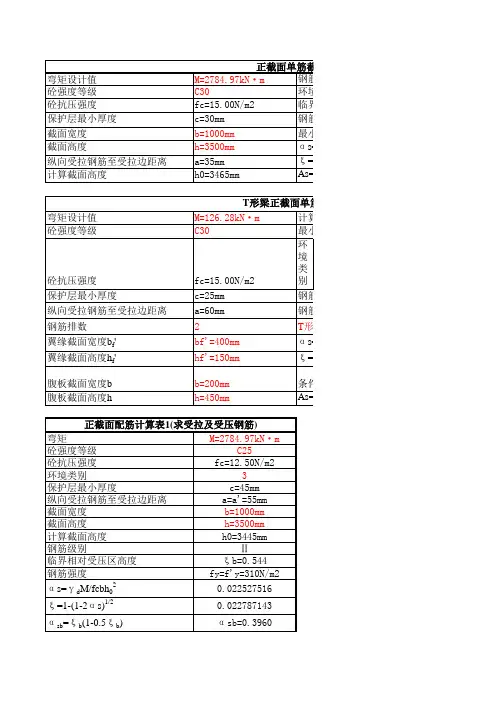
单筋T形梁正截面承载力计算首先，单筋T形梁的截面形状决定了其抗弯性能。

截面一般包括上翼缘、下翼缘和腹板三个部分。

上翼缘主要承担拉力，下翼缘和腹板主要承担压力。

根据材料的强度和构件尺寸，可以计算出单筋T形梁的截面性能指标，如截面面积、截面惯性矩、截面模量等。

其次，单筋T形梁的承载力计算还要考虑由荷载引起的应力。

常见的荷载包括自重、活载、风载和地震载等。

这些荷载可以综合考虑，并转化为梁的等效荷载作用于梁上。

根据不同的受力情况，可以采用弹性理论或塑性理论进行计算。

弹性理论假设材料的应力和应变满足胡克定律，可以解析地计算出梁的最大应力和变形情况。

而塑性理论假设材料达到屈服应变时，应力保持不变，可以通过平衡条件和塑性转化准则进行计算。

在设计和计算中，还需要考虑梁的安全性。

常见的安全系数包括抗弯强度安全系数、极限状态安全系数和服务状态安全系数等。

抗弯强度安全系数是指梁的抗弯强度与设计荷载之比，一般要求大于1.5、极限状态安全系数是指梁在极限状态下的荷载与承载力之比，要求大于1.0。

而服务状态安全系数是指梁在使用过程中的荷载与承载能力之比，要求大于 1.0。

最后，计算单筋T形梁的承载力还需要考虑构件的受限状况。

单筋T形梁的受限状态一般有局部屈曲、整体侧扭和挤压等。

这些受限状态会影响梁的承载能力。

为了确保梁的良好工作性能，需要对梁的限制状态进行合理的分析和计算。

综上所述，单筋T形梁的承载力计算是一个综合考虑材料、截面形状、荷载、安全性和受限状况等多个因素的过程。

只有在合理选择计算方法和参数的基础上，才能保证梁的设计符合规范，并能满足工程实际需求。

因此，在设计和计算单筋T形梁的承载力时，需要根据具体情况进行详细分析，并结合相关理论和规范进行计算，以保证构件的安全可靠性。

单筋T 形梁正截面承载力计算一、基本公式（一）第一类T 形梁2．第一类T 形梁的基本计算公式这一类梁的截面虽为T 形，但由于中和轴通过翼缘，即'f h x ≤，s y f c A f x b f ='1α⎪⎭⎫ ⎝⎛-'=≤201x h x b f M M f c u α 3．基本公式的适用条件是：1）0h x b ξ≤由于T 形截面的翼缘厚度h f ′一般都比较小，既然x ≤h f ′，因此这个条件通常都能满足，故不必验算。

2）0/bh A s =ρ应不小于min ρ（具体计算时，bh A A s S min min ,ρ=≥）（二）第二类T 形梁1．计算图式2．第二类T 形梁的基本计算公式这一类梁截面的中和轴通过肋部，即x > h f ′，故受压区为T 形。

于是第二类T 形梁正截面受弯承载力的基本计算公式可以写成：s y f f c c A f h b b f bx f ='-'+)(11αα()⎪⎪⎭⎫ ⎝⎛'-'-'+⎪⎭⎫ ⎝⎛-=≤220101f f f c c u h h h b b f x h bx f M M αα3．基本公式的适用条件1）为防止发生超筋破坏，应当满足：0h x b ξ≤ 或 b ξξ≤或 y c b s f f bh A //1011αξρ≤=或 ()b b c u bh f M ξξα5.012011-≤2）bhA A s s min min ,ρ=≥由于第二类T 形梁受压区较大，相应受拉钢筋也就较多，故一般均能满足此条件，可不必验算。

（三）T 形及倒L 形截面受弯构件受压区的翼缘计算宽度b f '应按表1各项中的最小值取用。

注：1、表中b 为梁的腹板宽度。

2、如肋形梁在梁跨内设有间距小于纵肋间距的横肋时，则可不遵守表列第三种情况的规定。

3、对有加腋的T 形和倒L 形截面，当受压区加腋的高度h h ≥h f ′，且加腋的宽度b h ≤3h h 时，则其翼缘计算宽度可按表列第三种情况规定分别增加2b h （T 形截面）和b h （倒L 形截面）采用。