人教版七年级数学下册 5.1 相交线 同步测试题(有答案)

七下数学同步练习、单元检测 第五章 相交线与平行线5.1.1 相交线复习检测（5分钟）：1、如图所示,∠1和∠2是对顶角的图形有( )A.1个B.2个C.3个D.4个2、如图，若∠1=60°，那么∠2=_______、∠3=_______、∠4=_______ .3、如图是一把剪刀，其中︒=∠401，则=∠2 ，其理由是 。

4、如图三条直线AB,CD,EF 相交于一点O, ∠AOD 的对顶角是_____,∠AOC 的邻补角是_______，若∠AOC=50°,则∠BOD=______,∠COB=_______，∠AOE+∠DOB+∠COF=_____.OF E D CBA5、如图，直线AB,CD 相交于O,OE 平分∠AOC,若∠AOD-∠DOB=50°,求∠EOB 的度数.OE D CBA6、如图,直线a,b,c 两两相交,∠1=2∠3,∠2=68°,求∠4的度数cba341212121221E(3)O D CBA (2)O D CBA (1)ODC BA5.1.2 垂线复习检测（5分钟）：1、两条直线互相垂直,则所有的邻补角都相等.( )2、一条直线不可能与两条相交直线都垂直.( )3、两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互相垂直.( )4、两条直线相交有一组对顶角互补，那么这两条直线互相垂直.( ).5、如图1,OA ⊥OB,OD ⊥OC,O 为垂足,若∠AOC=35°,则∠BOD=________.6、如图2,AO ⊥BO,O 为垂足,直线CD 过点O,且∠BOD=2∠AOC,则∠BOD=________.7、如图3,直线AB 、CD 相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE 与直线AB 的位置关系是_________. 8、已知:如图,直线AB,射线OC 交于点O,OD 平分∠BOC,OE 平分∠AOC.试判断OD 与OE 的位置关系.9、如图,AC ⊥BC,C 为垂足,CD ⊥AB,D 为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6，那么点C 到AB 的距离是_______,点A 到BC 的距离是________,点B 到CD 的距离是_____,A 、B 两点间的距离是_________.10、如图,在线段AB 、AC 、AD 、AE 、AF 中AD 最短.小明说垂线段最短, 因此线段AD 的长是点A 到BF 的距离,对小明的说法,你认为对吗？11、用三角尺画一个是30°的∠AOB,在边OA 上任取一点P,过P 作PQ ⊥OB,垂足为Q,量一量OP 的长,你发现点P 到OB 的距离与OP 长的关系吗?EODCBAFE D C B ADC BA5.1.3同位角、内错角、同旁内角复习检测（5分钟）：1、如图（4），下列说法不正确的是（）A.∠1与∠2是同位角B.∠2与∠3是同位角C.∠1与∠3是同位角D.∠1与∠4不是同位角2、如图（5），直线AB、CD被直线EF所截，∠A和是同位角，∠A和是内错角,∠A和是同旁内角.3、如图（6）, 直线DE截AB, AC, 构成八个角:①、指出图中所有的同位角、内错角、同旁内角.②、∠A与∠5, ∠A与∠6, ∠A与∠8, 分别是哪一条直线截哪两条直线而成的什么角？4、如图（7），在直角 ABC中，∠C＝90°，DE⊥AC于E,交AB于D .①、指出当BC、DE被AB所截时，∠3的同位角、内错角和同旁内角.②、若∠3+∠4=180°试说明∠1＝∠2＝∠3的理由.5.2.1平行线复习检测（5分钟）：1、在同一平面内,两条直线的位置关系有_________2、两条直线L1与L2相交点A，如果L1//L，那么L2与L（）3、在同一平面内,一条直线和两条平行线中一条直线相交,那么这条直线与平行线中的另一边必__________.8765c b a 34124、两条直线相交,交点的个数是________,两条直线平行,交点的个数是_____个. 判断题5、6、7、85、不相交的两条直线叫做平行线.( )6、如果一条直线与两条平行线中的一条直线平行, 那么它与另一条直线也互相平行.( )7、过一点有且只有一条直线平行于已知直线.( )8、读下列语句,并画出图形后判断.(1)直线a 、b 互相垂直,点P 是直线a 、b 外一点,过P 点的直线c 垂直于直线b. (2)判断直线a 、c 的位置关系,并借助于三角尺、直尺验证.9、试说明三条直线的交点情况,进而判定在同一平面内三条直线的位置情况.5.2.2平行线的判定复习检测（10分钟）：1、如图1所示,下列条件中,能判断AB ∥CD 的是( )A.∠BAD=∠BCDB.∠1=∠2;C.∠3=∠4D.∠BAC=∠ACD(1) (2) (3) （4）2、如图2所示,如果∠D=∠EFC,那么( )A.AD ∥BCB.EF ∥BCC.AB ∥DCD.AD ∥EF3、下列说法错误的是( ) A.同位角不一定相等 B.内错角都相等C.同旁内角可能相等D.同旁内角互补,两直线平行 4、如图5,直线a,b 被直线c 所截,现给出下列四个条件:•①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明 a ∥b 的条件序号为( ) （5） A.①② B.①③ C.①④ D.③④5、如图5,如果∠3=∠7,那么______ ,理由是 ;如果∠5=∠3,那么________, 理由是______________; 如果∠2+ ∠5= ______ 那么a ∥b,理由是________ .6、如图4,若∠2=∠6,则______∥______,如果∠3+∠4+∠5+∠6=180°, 那么____∥_______, 如果∠9=_____,那么AD ∥BC;如果∠9=_____,那么AB ∥CD.7、在同一平面内,若直线a,b,c 满足a ⊥b,a ⊥c,则b 与c 的位置关系是______.8、如图所示,BE 是AB 的延长线,量得∠CBE=∠A=∠C.(1)由∠CBE=∠A 可以判断______∥______,根据是_________.34D C BA 21F E D C B A 876543219654321D C B A DC D CBA 21(2)由∠CBE=∠C 可以判断______∥______,根据是_________. 9、已知直线a 、b 被直线c 所截,且∠1+∠2=180°试判断直线a 、b 的位置关系,并说明理由.10、如图，已知DG AEM ∠=∠，21∠=∠，试问EF 是否平行GH ，并说明理由.11、如图所示,已知∠1=∠2,AC 平分∠DAB,试说明DC ∥AB.12、如图所示,已知直线EF 和AB,CD 分别相交于K,H,且EG ⊥AB,∠CHF=600,∠E=30°,试说明AB ∥CD.GHKEDC B A13、提高训练:如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a 与c 平行吗?•为什么?D C B A O FE DC B AD C B A 187654321DC B AC A d ecb a 34125.3.1平行线的性质复习检测（10分钟）：1、如图1所示,AB ∥CD,则与∠1相等的角(∠1除外)共有( )A.5个B.4个C.3个D.2个(1) (2) （3）2、如图2所示,CD ∥AB,OE 平分∠AOD,OF ⊥OE,∠D=50°,则∠BOF 为( ) A.35° B.30° C.25° D.20°3、如图3所示,AB ∥CD,∠D=80°,∠CAD:∠BAC=3:2,则∠CAD=_______, ∠ACD=•_______.4、如图4,若AD ∥BC,则∠______=∠_______,∠______∠ABC+∠_______=180°; 若DC ∥AB,则∠______=∠∠________=∠__________,∠ABC+∠_________=180°（4） （5） （6）5、如图5,在甲、乙两地之间要修一条笔直的公路, 从甲地测得公路的走向是南偏西56°,甲、乙两地同时开工,若干天后公路准确接通, 则乙地所修公路的走向是_________,因为____________.6、河南)如图6所示,已知AB ∥CD,直线EF 分别交AB,CD 于E,F,EG •平分∠B-EF,若∠1=72°,则∠2=_______.7、如图，AB ∥CD ，∠1＝102°，求∠2、∠3、∠4、∠5的度数，并说明根据？8、如图，EF 过△ABC 的一个顶点A ，且EF ∥BC ，如果∠B ＝40°，∠2＝75°，那么∠1、∠3、∠C 、∠BAC ＋∠B ＋∠C 各是多少度，并说明依据？E21DCBNM G F E D CB A9、如图,已知:DE ∥CB,∠1=∠2,求证:CD 平分∠ECB.10、如图所示,把一张长方形纸片ABCD 沿EF 折叠,若∠EFG=50°,求∠DEG 的度数.11、如图所示，已知：AE 平分∠BAC ，CE 平分∠ACD ，且AB ∥CD ．求证：∠1+∠2=90°． 证明：∵ AB ∥CD ，（已知）∴∠BAC +∠ACD =180°，（ ） 又∵ AE 平分∠BAC ，CE 平分∠ACD ，（ ）∴112B AC ∠=∠，122A C D ∠=∠，( )∴001112()1809022B AC A CD ∠+∠=∠+∠=⨯=．即 ∠1+∠2=90°．结论：若两条平行线被第三条直线所截,则一组同旁内角的平分线互相 . 推广：若两条平行线被第三条直线所截,则一组同位角的平分线互相 .5.3.2命题、定理、证明复习检测（5分钟）：1、判断下列语句是不是命题（1）延长线段AB （ ） （2）两条直线相交，只有一交点（ ） （3）画线段AB 的中点（ ） （4）若|x|=2，则x=2（ ） （5）角平分线是一条射线（ ） 2、下列语句不是命题的是（ ）A.两点之间，线段最短B.不平行的两条直线有一个交点C.x 与y 的和等于0吗？D.对顶角不相等. 3、下列命题中真命题是（ ）A.两个锐角之和为钝角B.两个锐角之和为锐角C.钝角大于它的补角D.锐角小于它的余角4、命题：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对顶角；④同位角相等.其中假命题有（ ）A.1个B.2个C.3个D.4个 5、分别指出下列各命题的题设和结论（1）如果a ∥b ，b ∥c ，那么a ∥c （2）同旁内角互补，两直线平行 6、分别把下列命题写成“如果……，那么……”的形式（1）两点确定一条直线； （2）等角的补角相等； （3）内错角相等.7、如图,已知直线a 、b 被直线c 所截,在括号内为下面各小题的推理填上适当的根据:(1)∵a ∥b,∴∠1=∠3( ); (2)∵∠1=∠3,∴a ∥b( ); (3)∵a ∥b,∴∠1=∠2( ); (4) ∵a ∥b,∴∠1+∠4=180º ( ) (5)∵∠1=∠2,∴a ∥b( ); (6)∵∠1+∠4=180º,∴a ∥b( ). 8、已知：如图AB ⊥BC ，BC ⊥CD 且∠1=∠2，求证：BE ∥CF证明：∵AB ⊥BC ，BC ⊥CD （已知）∴ = =90°（ ） ∵∠1=∠2（已知）∴ = （等式性质）∴BE ∥CF （ ）9、已知：如图，AC ⊥BC ，垂足为C ，∠BCD 是∠B 的余角.求证：∠ACD=∠B证明：∵AC ⊥BC （已知）∴∠ACB=90°（ ） ∴∠BCD 是∠ACD 的余角∵∠BCD 是∠B 的余角（已知）∴∠ACD=∠B （ ）5.4 平移复习检测（5分钟）：1、下列哪个图形是由左图平移得到的（ ）D2、如图所示,△FDE 经过怎样的平移可得到△ABC.( ) A.沿射线EC 的方向移动DB 长; B.沿射线EC 的方向移动CD 长 C.沿射线BD 的方向移动BD 长; D.沿射线BD 的方向移动DC 长ab 1 23c4C A BD EF1 2 BD CFED C BA3、下列四组图形中,•有一组中的两个图形经过平移其中一个能得到-另一个,这组图形是( )4、如图所示,△DEF 经过平移可以得到△ABC,那么∠C的对应角和ED 的对应边分-别是( ) A.∠F,AC B.∠BOD,BA; C.∠F,BA D.∠BOD,AC 5、在平移过程中,对应线段( ) A.互相平行且相等; B.互相垂直且相等 C.互相平行(或在同一条直线上)且相等6、在平移过程中,平移后的图形与原来的图形________和_________都相同,•因-此对应线段和对应角都________.7、如图所示,平移△ABC 可得到△DEF,如果∠A=50°,∠C=60°,那么∠E=•____-度,∠EDF=_______度,∠F=______度,∠DOB=_______度.8、将正方形ABCD 沿对角线AC 方向平移，且平移后的图形的一个顶点恰好在AC 的中点O 处，则移动前后两个图形的重叠部分的面积是原正方形面积的_______9、直角△ABC 中，AC ＝3cm ，BC ＝4cm ，AB ＝5cm ，将△ABC 沿CB 方向平移3cm ，则边AB 所经过的平面面积为＿＿＿＿cm 2。

人教版七年级数学下册第五章订交线与平行线5.1 订交线同步练习一、单项选择题（共10 题；共 30 分）1.以以下列图，∠ 1 和∠ 2 是对顶角的图形有 ( )A. 1 个B. 个2C.个3D. 个42.如图，以下说法不正确的选项是（）A. ∠1 和∠ 2 是同旁内角B.∠ 1 和∠ 3 是对顶角C.∠ 3 和∠ 4 是同位角D.∠ 1 和∠ 4 是内错角3.以以下列图，∠ 1 和∠ 2 是对顶角的是（）A. B. C. D.4.以下说法中正确的个数为（）① 两条直线订交成四个角，若是有两个角相等，那么这两条直线垂直；② 两条直线订交成四个角，若是有一个角是直角，那么这两条直线垂直；③ 一条直线的垂线能够画无数条；④ 在同一平面内，经过一个已知点能画一条且只能画一条直线和已知直线垂直．5.如图，∠ 1=15 °，∠ AOC=90°，点 B， O，D 在同素来线上，则∠ 2 的度数为（）A.75 °B.15 °C.105 °D.165 °6.以以下列图，以下说法错误的选项是（）A. ∠A 和∠ B 是同旁内角B. ∠A 和∠ 3 是内错角C. ∠ 1 和∠ 3 是内错角D. ∠ C 和∠ 3 是同位角17.如图，三条直线订交于点O．若 CO⊥ AB，∠ 1=56 °，则∠ 2 等于（）A.30 °B. 34C. 45 °D. 56 °°8. 在以下语句中，正确的选项是（）．A. 在平面上，一条直线只有一条垂线;B. 过直线上一点的直线只有一条;C. 过直线上一点且垂直于这条直线的直线有且只有一条;D. 垂线段就是点到直线的距离9. 如图，以下 6 种说法：① ∠1与∠4 是内错角；② ∠ 1 与∠ 2 是同位角；③ ∠2 与∠ 4 是内错角；④ ∠4 与∠ 5 是同旁内角；⑤ ∠2 与∠ 4 是同位角；⑥ ∠2 与∠ 5 是内错角．其中正确的有( )A. 1 个B. 个2C.个3D. 个410.以以下列图， OA⊥ OC， OB⊥ OD，下面结论中，其中说法正确的选项是（）① ∠AOB＝∠ COD；② ∠ AOB＋∠ COD＝ 90°；③ ∠BOC＋∠ AOD＝180 °；④ ∠ AOC－∠ COD＝∠ BOC.A. ①②③B. ①②④C. ①③④D. ②③④二、填空题（共10 题；共 30 分）11.如图，直线AB， CD 订交于点O， EO⊥ AB，垂足为点O，若∠ AOD=132°，则∠ EOC=________12.如图，已知直线AB 与 CD 订交于点O， OA 均分∠ COE，若∠ DOE=70°，则∠ BOD=________．13.如图，∠ 1 和∠ 2 是 ________角，∠ 2 和∠ 3 是 ________角。

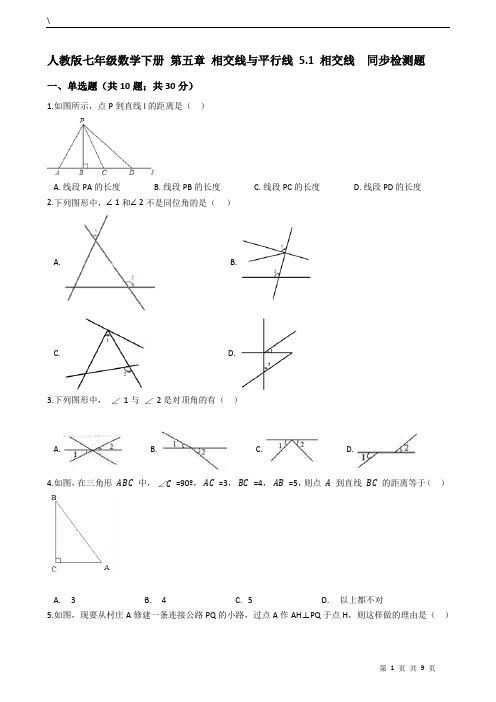
人教版七年级数学下册第五章相交线与平行线 5.1 相交线同步检测题一、单选题（共10题；共30分）1.如图所示，点P到直线l的距离是（）A. 线段PA的长度B. 线段PB的长度C. 线段PC的长度D. 线段PD的长度2.下列图形中，∠1和∠2不是同位角的是（）A. B.C. D.3.下列图形中，∠1与∠2是对顶角的有（）A. B. C. D.4.如图，在三角形中，∠=90º，=3，=4，=5，则点到直线的距离等于（）A. 3B. 4C. 5D. 以上都不对5.如图，现要从村庄A修建一条连接公路PQ的小路，过点A作AH⊥PQ于点H，则这样做的理由是（）A. 两点之间线段最短B. 两点确定一条直线C. 垂线段最短D. 过一点可以作无数条直线6.下图中∠与∠是内错角的是（）A. B.C. D.7.下列图形中，∠1和∠2是同位角的是（）A. B. C. D.8.某城市有四条直线型主干道分别为l1，l2，l3，l4，l3和l4相交，l1和l2相互平行且与l3、l4相交成如图所示的图形，则共可得同旁内角（）对．A. 4B. 8C. 12D. 169.如图，直线AB，CD相交于点O，下列描述：①∠1和∠2互为对顶角②∠1和∠3互为对顶角③∠1=∠2④∠1=∠3其中，正确的是（）A. ①③B. ①④C. ②③D. ②④10.如图，直线AB与CD相交于点O，若∠AOC= ∠AOD，则∠BOD的度数为（）A. 30°B. 45°C. 60°D. 135°二、填空题（共10题；共30分）11.如图，已知直线AB、CD、EF相交于点O，∠1=95°，∠2=32°，则∠BOE=________.12.用剪刀剪东西时，剪刀张开的角度如图所示，若∠1=25°，则∠2=________13.如图所示，已知AB和CD相交于O，OA平分∠EOC，∠EOC=70°，则∠BOD=________14.如图，AH⊥BC，垂足为H，若AB=1.7cm,AC=2cm,AH=1.1cm，则点A到直线BC的距离是________cm .15.有4条直线a、b、c、d以及3个交点A、B、C，在图中画出的部分可以数出________对同位角．16.如图，与图中的∠1成内错角的角是________．17.如图，直线AB、CD被EF、EC所截，在∠1、∠2、∠3、∠4、∠5、∠6中，同位角有________个．18.如图，如果∠2=100°，那么∠1的同旁内角等于________度．19.在同一平面内，若a⊥b，a⊥c，则b与c的位置关系是________．20.如图，与图中的∠1成内错角的角是________．三、解答题（共8题；共40分）21.如图，某村庄计划把河中的水引到水池M中，怎样开的渠最短，为什么？（保留作图痕迹，不写作法和证明）说明理由22.如图，直线a，b相交，∠1=40°，求∠2、∠3、∠4的度数．23.如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.24.如图，直线AD与AE相交于点A，直线BC分别交AD、AE于点B、C，直线DE分别交AD、AE于点D、E，分别写出图中的两对同位角、两对内错角、两对同旁内角．25.如图所示，∠1与∠2，∠3与∠4之间各是哪两条直线被哪一条直线所截而形成的什么角？26.图中的∠1与∠C、∠2与∠B、∠3与∠C，各是哪两条直线被哪一条直线所截形成的同位角？27.如图，直线AB、CD相交于点O，OF⊥CO，∠AOF与∠BOD的度数之比为3：2，求∠AOC的度数．28.如图所示，直线AB与CD交于点O，MO⊥AB，垂足为O，ON平分∠AOD．若∠COM=50°，求∠AON 的度数．答案解析部分一、单选题1.【答案】B2.【答案】D3.【答案】A4.【答案】A5.【答案】C6.【答案】A7.【答案】D8.【答案】D9.【答案】D10.【答案】B二、填空题11.【答案】53°12.【答案】25°13.【答案】：°14.【答案】1.115.【答案】1216.【答案】∠BDC17.【答案】318.【答案】10019.【答案】平行20.【答案】∠BDC三、解答题21.【答案】解：理由是：垂线段最短.22.【答案】解：∵∠1=40°，∴∠3=∠1=40°，∴∠2=∠4=180°-∠1=180°-40°=140°23.【答案】解：∵∠2=65°∴∠1=∠2=65°（对顶角相等）又∠1=2∠3∴∠3= ∠1=32.5°∴∠4=∠3=32.5°（对顶角相等）24.【答案】解：图中的2对同位角：∠1与∠2，∠3与∠4；图中的2对内错角：∠5与∠2，∠6与∠4；图中的2对同旁内角：∠1与∠3，∠2与∠4．25.【答案】解：解：左图：∠1与∠2是AB与CD被直线BD所截形成的内错角，∠3与∠4是直线AD与直线BC被直线BD所截形成的内错角；右图：∠1与∠2是AB与CD被直线BD所截形成的同旁内角，∠3与∠4是直线AD与直线BC被直线AB所截形成的同位角26.【答案】解：在截线的同旁找同位角．如图，∠1与∠C是直线DE、BC被直线AC所截形成的同位角，∠2与∠B是直线DE、BC被直线AB所截形成的同位角，∠3与∠C是直线DF、AC被直线BC所截形成的同位角27.【答案】解：∵OF⊥CO，∴∠AOF+∠AOC=90°，∵∠AOC=∠BOD，∴∠AOF+∠BOD=90°，∵∠AOF与∠BOD的度数之比为3：2∴∠AOF= ．28.【答案】解：∵MO⊥AB，∴∠AOM=90°，∵∠COM=50°，∴∠AOD=180°﹣90°﹣50°=40°，∵ON平分∠AOD，∴∠AON= ∠AOD= ×40°=20°。

(直打版)人教版七年级下册第五章相交线与平行线5.1相交线同步练习题含答案(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(直打版)人教版七年级下册第五章相交线与平行线5.1相交线同步练习题含答案(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(直打版)人教版七年级下册第五章相交线与平行线5.1相交线同步练习题含答案(word版可编辑修改)的全部内容。

初一数学人教版七年级下册第五章　相交线与平行线5．1　相交线同步练习题1. 下列说法中正确的是( )A．不相等的角一定不是对顶角B．互补的两个角是邻补角C．互补且有一条公共边的两个角是邻补角D．两条直线相交所成的角是对顶角2. 下列说法正确的是（ )A．在同一平面内，过直线外一点向该直线画垂线，垂足一定在该直线上B．在同一平面内，过线段或射线外一点向该线段或射线画垂线，垂足一定在该线段或射线上C．过线段或射线外一点不一定能画出该线段或射线的垂线D．过直线外一点与直线上一点画的一条直线与该直线垂直3. 已知∠α和∠β的对顶角，若∠α＝60°，则∠β的度数为( ）A．30° B．60° C．70° D．150°4。

如图,直线AB，CD相交于点O，因为∠1＋∠3＝180°，∠2＋∠3＝180°，所以∠1＝∠2,其推理依据是（ )A．同角的余角相等 B．对顶角相等C．同角的补角相等 D．等角的补角相等5. 如图，OB⊥CD于点O,∠1＝∠2，则∠2与∠3的关系是（ )A．∠2＝∠3 B．∠2与∠3互补C．∠2与∠3互余 D．不能确定6。

5.1 相交线垂线段基础训练知识点1 垂线段的定义1.下列说法正确的是()A.垂线段就是垂直于已知直线的线段B.垂线段就是垂直于已知直线并且与已知直线相交的线段C.垂线段是一条竖起来的线段D.过直线外一点向该直线作垂线,这一点到垂足之间的线段叫垂线段2.如图,下列说法不正确的是()A.点B到AC的垂线段是线段ABB.点C到AB的垂线段是线段ACC.线段AC是点A到BC的垂线段D.线段BD是点B到AD的垂线段知识点2 垂线段的性质3.如图,计划在河边建一水厂,过C点作CD⊥AB于D点.在D点建水厂,可使水厂到村庄C的路程最短,这样设计的依据是__________.4.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在()A.A点B. B点C.C点D.D点5.如图,已知AC⊥BC,CD⊥AB,垂足分别是C,D,那么以下线段大小的比较必定成立的是()A.CD>ADB.AC<BCC.BC>BDD.CD<BD6.如图,AD⊥BD,BC⊥CD,AB=6 cm,BC=4 cm,则BD的长度的取值范围是()A.大于4 cmB.小于6 cmC.大于4 cm或小于6 cmD.大于4 cm且小于6 cm7.如图,在三角形ABC中,∠C=90°,AC=3,点P可以在直线BC上自由移动,则AP的长不可能是()A.2.5B.3C.4D.5知识点3 点到直线的距离8.如图所示的是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段的长度.9.下列图形中,线段PQ的长表示点P到直线MN的距离的是()10.如图,其长能表示点到直线(线段)的距离的线段的条数是()A.3B.4C.5D.611.如图,三角形ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是()A.线段CA的长B.线段CD的长C.线段AD的长D.线段AB的长12.点到直线的距离是指()A.直线外一点到这条直线的垂线的长度B.直线外一点到这条直线上的任意一点的距离C.直线外一点到这条直线的垂线段D.直线外一点到这条直线的垂线段的长度13.如图,AB⊥AC,AD⊥BC,如果AB=4 cm,AC=3 cm,AD=2.4 cm,那么点C到直线AB的距离为()A.3 cmB.4 cmC.2.4 cmD.无法确定易错点对垂线段的性质理解不透彻而致错14.点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离()A.等于4 cmB.等于2 cmC.小于2 cmD.不大于2 cm提升训练考查角度1 利用点到直线的距离的定义进行识别15.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有()A.2条B.3条C.4条D.5条考查角度2 利用作垂线法作图16.如图,已知钝角三角形ABC中,∠BAC为钝角.(1)画出点C到AB的垂线段;(2)过点A画BC的垂线;(3)画出点B到AC的垂线段,并量出其长度.考查角度3 利用垂线段的性质比较大小17.如图,直线AB,CD相交于点O,P是CD上一点.(1)过点P画AB的垂线段PE;(2)过点P画CD的垂线,与AB相交于F点;(3)说明线段PE,PO,FO三者的大小关系,其依据是什么?考查角度4 利用垂线段的性质解实际应用题18.如图,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄,设汽车行驶到点P位置时,离村庄M最近,行驶到点Q位置时,离村庄N最近,请你在AB上分别画出P,Q两点的位置.探究培优拔尖角度1 利用垂线段的性质进行方案设计(建模思想)19.如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.(1)不考虑其他因素,请你画图确定蓄水池H的位置,使它到四个村庄的距离之和最小;(2)计划把河水引入蓄水池H中,怎样开渠最短?并说明根据.拔尖角度2 利用垂线段的性质解决绝对值问题(数形结合思想)20.在如图所示的直角三角形ABC中,斜边为BC,两直角边分别为AB,AC,设BC=a,AC=b,AB=c.(1)试用所学知识说明斜边BC是最长的边;(2)试化简|a-b|+|c-a|+|b+c-a|.参考答案1.【答案】D2.【答案】C3.【答案】垂线段最短4.【答案】A5.【答案】C6.【答案】D解：根据“垂线段最短”可知BC<BD<AB,所以BD大于4 cm且小于6 cm.7.【答案】A8.【答案】BN或AM9.【答案】A解：对于选项A,PQ⊥MN,Q是垂足,故线段PQ的长为点P到直线MN 的距离.10.【答案】C解：线段AB的长度可表示点B到AC的距离,线段CA的长度可表示点C到AB的距离,线段AD的长度可表示点A到BC的距离,线段CD 的长度可表示点C到AD的距离,线段BD的长度可表示点B到AD的距离,所以共有5条.11.【答案】B12.【答案】D13.【答案】A解：因为AB⊥AC,所以点C到直线AB的距离是线段AC的长度,即3 cm.14.错解:B诊断:点到直线的距离是指这个点到直线的垂线段的长度.虽然垂线段最短,但是并没有说明PC是垂线段,所以垂线段的长度可能小于2 cm,也可能等于2 cm.正解:D15.【答案】D16.解:如图:(1)CD即为所求;(2)直线AE即为所求;(3)BF即为所求.长度略.17.解:(1)如图所示.(2)如图所示.(3)PE<PO<FO,其依据是垂线段最短.18.解:如图所示.19.解:(1)如图,连接AD,BC,交于点H,则H点为蓄水池的位置,它到四个村庄的距离之和最小.(2)如图,过点H作HG⊥EF,垂足为G,则沿HG开渠最短.根据:连接直线外一点与直线上各点的所有线段中,垂线段最短.分析：本题考查了垂线段的性质在实际生活中的运用.体现了建模思想的运用.20.解:(1)因为点C与直线AB上点A,B的连线中,CA是垂线段,所以AC<BC.因为点B与直线AC上点A,C的连线中,AB是垂线段,所以AB<BC.故AB,AC,BC中,斜边BC最长.(2)因为BC>AC,AB<BC,AC+AB>BC,所以原式=a-b-(c-a)+b+c-a=a.。

人教版数学七年级下册第五章《相交线》真题同步测试1（含解析）综合考试注意事项：1、填写答题卡的内容用2B铅笔填写2、提前 xx 分钟收取答题卡第Ⅰ卷 客观题第Ⅰ卷的注释阅卷人一、单选题（每题4分，共40分）得分1．（2022·自贡）如图，直线 AB、CD 相交于点 O ；若 ∠1=30∘ ，则 ∠2 的度数是（ ）A．30°B．40°C．60°D．150°2．（2019七下·黄骅期末）如图，点O在直线AB上，OC为射线，∠2比∠1的3倍少20°，则∠1的度数为（ ）A．35°B．45°C．50°D．130°3．（2022·衢州模拟）如图，直线m∥n，则∠α为（ ）A．70°B．65°C．50°D．40°⊥，垂足为O，EF为过点O的一条直线，则∠1与∠2的关系一定成立的是（4．已知：如图，AB CD）A．相等B．互余C．互补D．互为对顶角⊥于O，且∠COE =50°，则5．（2017七下·北京期中）如图，直线AB、CD相交于点O，EF AB∠BOD等于（ ）A．40°B．45°C．55°D．65°6．（2022七下·海曙期末）下列说法错误的是（ ）A．对顶角相等B．同位角相等C．同角的余角相等D．同角的补角相等7．（2022七下·温州期中）如图，∠1与∠2是（ ）A．对顶角B．同位角C．内错角D．同旁内角8．（2019八上·海口期中）下列命题是真命题的是（ ）A．直角三角形中两个锐角互补B．相等的角是对顶角C．同旁内角互补，两直线平行D．若 ¿a∨¿∨b∨¿ ，则 a=b 9．（2021七下·桓台期中）如图，将长方形ABCD沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠AGE=34°，则∠BHG等于（ ）A．73°B．34°C．45°D．30°10．下列语句错误的是（ ）A．连接两点的线段的长度叫做两点间的距离B．两条直线平行，同旁内角互补C．若两个角有公共顶点且有一条公共边，和等于平角，则这两个角为邻补角D．平移变换中，各组对应点连成两线段平行且相等阅卷人二、填空题（每题4分，共28分）得分11．（2016七下·邹城期中）如图是一把剪刀，其中∠1=40°，则∠2= ．12．（2023七下·上海期末）若∠1的对顶角是∠2，∠2的邻补角是∠3，∠3的余角是∠4，若∠4=55°，则∠1＝ °．∠＝80°，则∠AOC＝ 度．13．（2021七下·九江期中）如图是一把剪刀，若∠AOB+COD⊥，∠AOC=50°，则∠BOE= 14．（2019七下·桂林期末）如图，AB，CD相交于点O，EO CD°．15．（2020七上·绿园期末）如图，直线 AB，CD 相交于点 O ， OE⊥AB 于点 O ，且∠COE=48° ，则 ∠AOD 为 ．16．（2022七下·崇川期末）如图，七边形ABCDEFG中，AB，ED的延长线交于点O，若∠1，∠2，∠3，∠4对应的邻补角和等于220°，则∠BOD等于 ．17．（2021九上·长沙期中）如图，直线a，b被直线c所截，已知a∥b，∠1=130°，则∠2为 度．第Ⅱ卷 主观题第Ⅱ卷的注释阅卷人三、解答题（共82分）得分⊥，已知∠BOD 18．（11分）（2020七上·越城期末）如图，直线AB与直线CD相交于点O，OE AB＝45°，求∠COE的度数．19．（10分）如图，已知直线AB和CD相交于O点，∠COE=90°，OF平分∠AOE，∠COF=28°，求∠BOD 的度数．20．（12分）（2021八下·黄州期末）如图是根据四边形的不稳定性制作的边长为15cm 的可活动菱形衣架.若墙上钉子间的距离AB ＝BC ＝15cm ，求∠1的度数.21．（11分）（2021七下·峨山期末）如图，直线AB ，CD ，EF 相交于点O ．如果∠BOD ＝60°，EF 垂直于AB 于点O ，求∠AOD 和∠FOC 的度数．22．（12分）如图，已知AB /¿CD ，FE 平分 ∠GFD ，GF 交AB 于点 M ，∠GMA =52° ，求 ∠BEF 的度数.23．（13分）（2020七下·西吉期末）如图，AB 、CD 相交于点O ，∠A=1∠，∠B=2∠，则∠C= D.∠理由是：∵ ∠A=1∠，∠B=2∠，（已知）且∠1=2∠（ ▲ ）∴∠A= B.∠（等量代换）∴AC BD ∥（ ▲ ）.∴∠C=D ∠（ ▲ ）.24．（13分）（2020七下·太原期中）如图，E 为DF 上的点，B 为AC 上的点，DF AC ∥，∠C ＝∠D ，判断∠1＝∠2是否成立，并说明理由．答案解析部分1．【答案】A【解析】【解答】解：∵直线AB，CD交于点O，∠∠∴1=2=30°.故答案为：A.【分析】利用对顶角相等，可求出∠2的度数.2．【答案】C∠﹣．【解析】【解答】由题意知：∠2=3120°∠，∵∠1+2=180°∠﹣，∴∠1+3120°=180°解得：∠1=50°．故答案为：C．∠﹣、∠1+2=180°∠求解可得．【分析】根据∠2=3120°3．【答案】C【解析】【解答】解：如图：根据邻补角可得：∠1=180°-130°=50°，∵m∥n，∠，∴∠α=1=50°故答案为：C.【分析】由邻补角的定义可得∠1的度数，再根据二直线平行，同位角相等可得∠α的度数. 4．【答案】B∠，选【解析】【分析】依题意知，∠1和∠AOF为对顶角，且∠2和∠AOF互余，所以∠2+1=90°B．【点评】本题难度较低，主要考查学生对对顶角性质和互余知识点的掌握．5．【答案】A⊥于O，∠COE=50°，【解析】【解答】∵EF AB∴∠AOC=90°-50°=40°，∵∠AOC与∠BOD是对顶角，∠；∴∠BOD=AOC=40°故答案为：A.【分析】两直线相交，所形成的的对顶角相等.6．【答案】B【解析】【解答】解：对顶角相等，正确，不符合题意；B、两直线平行，同位角相等，错误，符合题意；C、同角的余角相等，正确，不符合题意；D、同角的补角相等，正确，不符合题意；故答案为：B.【分析】根据对顶角的性质判断A；根据平行线的性质判断B；根据余角或补角的性质判断CD. 7．【答案】C【解析】【解答】解：根据内错角的定义，结合图形可知：∠1与∠2是内错角.故答案为：C.【分析】两条直线被第三条直线c所截，在截线的同旁，且在被截两直线的同一侧的角，我们把这样的两个角称为同位角；两条直线被第三条直线所截，在截线同旁，且在被截线之内的两角，叫做同旁内角；两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角叫做内错角.如果一个角的两边分别是另一个角两边的反向延长线，且这两个角有公共顶点，那么这两个角是对顶角.8．【答案】C【解析】【解答】解：A、直角三角形中两个锐角互余，故此选项错误；B、相等的角不一定是对顶角，故此选项错误；C、同旁内角互补，两直线平行，正确；D、若|a|=|b|，则a=±b，故此选项错误；故答案为：C.【分析】A、直角三角形中两个锐角互余，据此判断即可；B、对顶角相等，但相等的角不一定是对顶角，据此判断即可；C、同旁内角互补，两直线平行，据此判断即可；D、若|a|=|b|，则a=±b，据此判断即可.9．【答案】A【解析】【解答】解：∵∠AGE=34°，∴∠DGE=146°，由折叠可得， ∠DGH=∠EGH=12∠DGE=73°，∵AD/¿BC，∴∠BHG=∠DGH=73°．故答案为：A．【分析】先求出 ∠DGE，由折叠可得，∠DGH=∠EGH=12∠DGE，根据平行线的性质可得∠BHG=∠DGH。

人教版七年级数学下册《5.1.1相交线》同步提升训练(带答案)学校:___________班级：___________姓名：___________考号：___________一、单选题1．在同一平面内，三条直线的交点个数不能是（ ）．A ．1个B ．2个C ．3个D ．4个 2．下面四个图中，1∠与2∠是对顶角的是（ ） A ． B ．C ．D ．3．已知1∠与2∠是邻补角，2∠是3∠的邻补角，那么1∠与3∠的关系是（ ）A ．对顶角B ．相等但不是对顶角C ．邻补角D ．互补但不是邻补角4．如图，直线AB CD ，相交于点O ，2AOD DOE ∠=∠若30BOE ∠=︒，则AOC ∠的度数为（ ）A ．25︒B ．30︒C ．40︒D ．45︒5．直线3l 与12,l l 相交得如图所示的5个角，其中互为对顶角的是（ ）A ．3∠和5∠B ．3∠和4∠C ．1∠和5∠D ．1∠和4∠6．如图115∠=︒，=90AOC ︒∠点B ，O ，D 在同一直线上，则2∠的度数为( )A ．95︒B ．115︒C ．105︒D ．165︒7．如图，两条直线AB 与CD 相交于点O ，OE 是射线，则图中共有邻补角和对顶角的数量分别为（ ）A ．6对，2对B ．4对，2对C ．8对，4对D ．4对，4对 8．按下列语句画图：点A 在直线m 上，也在直线n 上，但不在直线c 上，且直线m n c 、、两两相交，下列图形符合题意的是（ ）A ．B ．C ．D ．9．如图，直线,AB CD 相交于点O ．若12120∠+∠=︒，3125∠=︒则2∠的度数是（ ）A ．37.5︒B ．75︒C ．50︒D ．65︒二、填空题11．如图，直线a 、b 相交1392∠+∠=︒，则2∠= ．12．2∠与1∠互为邻补角，且2∠比1∠的3倍还多20︒，则1∠的度数是 °． 13．如图，直线AB 和CD 相交于点O ，则∠AOC 的邻补角是 .14．如图，CO∠AB ，垂足为O ，∠COE ﹣∠BOD=4°，∠AOE+∠COD=116°，则∠AOD= °．三、解答题15．如图所示，已知65AOF ∠=︒，:2:3∠∠=BOC EOC 计算AOC ∠的大小．16．如图，直线AB ，CD 相交于点O ，OA 是COE ∠的平分线．(1)若92DOE ∠=︒，求BOD ∠的度数；(2)若:7:8COE DOE ∠∠=，求BOD ∠的度数．17．如图，点A O B 、、在同一直线上，射线OD OE 、分别平分,AOC BOC ∠∠．(1)依题意补全图形；(2)DOE ∠度数是________；(3)若130BOC ∠=︒，求AOE ∠的度数．参考答案：1．D2．D3．A4．C5．A6．C7．A8．D9．D10．111．134︒12．4013．∠AOD 和∠BOC14．15015．154AOC ∠=︒16．(1)44BOD ∠=︒；(2)42BOD ∠=︒．17．(1)(2)90°(3)115°。

初中数学同步训练必刷题（人教版七年级下册5.1.1 相交线）一、单选题1．（2022七下·承德期末）下列四个图形中，∠1与∠2是对顶角的是（）A．B．C．D．2．（2022七上·南海期中）直线AB和直线CD相交于点O，若∠AOC＝40°，则∠BOC等于（）A．140°B．60°C．40°D．160°3．（2022七下·崇川期末）如图，直线AB与CD相交于点O，∠AOC：∠AOD＝2：3，则∠BOD等于（）A．36°B．72°C．60°D．75°（4．（2022九上·南宁开学考）如图，直线AB，CD相交于点O，OA平分∠EOC，∠EOC＝110°，则∠BOC 的度数是（）A．115°B．125°C．135°D．145°5．（2022七下·承德期末）如图，小明手持手电筒照向地面，手电筒发出的光线CO与地面AB形成了两个角，∠BOC＝8∠AOC，则∠BOC的度数是（）A．160°B．150°C．120°D．20°6．（2022七下·延庆期末）如图，直线AB，CD相交于点O，如果∠1=35°，那么∠2的度数是（）A．35°B．55°C．145°D．165°7．（2022七下·钦州期末）如图，直线AB，CD，EO相交于点O，已知OA平分∠EOC，若∠EOC：∠EOD ＝2：3，则∠BOD的度数为（）A．40°B．37°C．36°D．35°8．（2022七下·东明期末）如图，直线AB、CD相交于点O，且∠AOC+∠BOD=110°，则∠AOD的度数为（）A．125°B．120°C．110°D．100°9．（2022七下·青县期末）如图，直线AB、CD相交于点O，下列描述一定正确的是（）A．∠1和∠2互为对顶角B．∠1和∠3互为邻补角C．∠1=∠2D．∠1=∠310．（2022七下·江油期中）如图，直线AB、CD相交于O，OA平分∠EOC，若∠EOC=70°，那么∠BOD 的度数是（）A．30°B．35°C．45°D．40°二、填空题11．（2022七下·五常期末）若∠1和∠2是对顶角，∠1＝36°，则∠2的度数是度．12．（2022七下·大连期末）如图，∠1与∠2是对顶角，∠1=α+10°，∠2=40°，则α=°．13．（2022七下·富川期末）如图，直线AB，CD相交于点O，OE是∠AOD的平分线，若∠BOD=40°，则∠COE的度数为．14．（2022七下·榆林期末）若∠1与∠2是对顶角，∠3与∠2互余，且∠3=37∘，则∠1的度数为°. 15．（2022七下·雨花期末）如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE．若∠AOC=76°，则∠BOF的度数为°．16．（2022七下·义乌开学考）如图，点O 在直线AB 上，过点O 作射线OC，若∠AOC=53°17′28″，则∠BOC 的度数是．17．（2021七下·涿鹿期末）在同一平面内的三条直线，它们的交点个数可能是．18．（2021七下·玉林期末）如图，两直线交于点O，若∠3＝3∠2，则∠1的度数是.19．（2021七下·孝义期中）如图是某城市一座古塔底部平面图，在不能进入塔内测量的情况下，学习兴趣小组设计了如图所示的一种测量方案，学习兴趣小组认为测得∠COD的度数就是∠AOB的度数．其中的数学原理是．20．（2021七下·滦南期末）小明用一副三角板自制对顶角的“小仪器”，第一步固定直角三角板ABC，并将边AC延长至点P，第二步将另一块三角板CDE的直角顶点与三角板ABC的直角顶点C 重合，摆放成如图所示，延长DC至点F，∠PCD与∠ACF就是一组对顶角，若∠ACF=30∘，则∠PCD=，若重叠所成的∠BCE=n∘(0∘<n<90∘)，则∠PCF的度数．三、解答题21．（2022七下·中山期末）如图，直线AB，CD相交于点O，OE平分∠BOC，OF∠CD，若∠BOE＝72°，求∠AOF的度数．22．（2022七下·韩城期中）如图，直线AB，CD相交于点O，∠BOC=125°，∠AOE=∠BOD，求∠DOE的度数.23．（2022七下·河源期中）如图，直线a，b相交于点O，已知3∠1−∠2=100°，求∠3的度数．24．（2021七下·南沙期中）如图，直线AB、CD、EF相交于点O，OG平分∠COF，∠1=30°，∠2=45°．求∠3的度数．25．（2022七下·黄州期中）如图，直线AB、CD相交于点O，OE平分∠BOD，∠AOC=72°，∠DOF=90°．（1）求∠DOE的度数；（2）求∠EOF的度数．26．（2021七下·瑶海期末）如图，直线AB，CD和EF相交于点O，（1）写出∠AOC，∠BOF的对顶角；（2）如果∠AOC=70°，∠BOF=20°，求∠BOC和∠DOE的度数．27．（2021七下·武昌期中）如图，直线MD、CN相交于点O，OA是∠MOC内的一条射线，OB是∠NOD 内的一条射线，∠MON＝70°.（1）若∠BOD＝12∠COD，求∠BON的度数；（2）若∠AOD＝2∠BOD，∠BOC＝3∠AOC，求∠BON的度数.28．如图，直线AB、CD相交于点O，OE把∠BOD分成两部分，（1）直接写出图中∠AOC的对顶角为, ∠BOE的邻补角为；（2）若，且=2：3，求的度数.答案解析部分1．【答案】C【知识点】对顶角及其性质【解析】【解答】解：对顶角指的是有一个公共顶点，并且一个角的两边是另一个角两边的反向延长线的两个角，所以：A 、两角没有公共顶点，不符合题意；B 、两角也是只有一条边互为反向延长线，另一条边没有互为反向延长线，不符合题意；C 、两角有一个公共顶点，并且一个角的两边是另一个角两边的反向延长线的两个角，符合题意；D 、两角只有一条边互为反向延长线，另一条边没有互为反向延长线，不符合题意； 故答案为：C ．【分析】有一个公共顶点，并且一个角的两边是另一个角两边的反向延长线的两个角是对顶角，据此逐一判断即可.2．【答案】A 【知识点】邻补角【解析】【解答】解：∵∠AOC=40°，∴∠BOC=180°-∠AOC=180°-40°=140°， 故答案为：A ．【分析】利用邻补角求出∠BOC 的度数即可。

寒假预习《5.1.1 相交线》同步测试培优卷精选 2021-2022学年人教版数学七年级下册（含答案）一、精心选一选1. 根据语句“直线1l与直线2l相交，点M在直线1l上，直线2l不经过点M．”画出的图形是（）A．B．C．D．2. 下列各图中，∠1和∠2是对顶角的是( )A．B．C．D．3. 如图，对顶角量角器中α∠的度数为（）A．120°B．60°C．90°D．50°4. 下面各图中∠1和∠2是对顶角的是（）A．B．C ．D ．5. 如图，直线AB ，CD 交于点O ，射线OM 平分∠AOD ，若∠BOD=760，则∠BOM等于（ ）A ．B ．C ．D ．6. 两条直线相交于一点，则共有对顶角的对数为（ ）A ．1对B ．2对C ．3对D ．4对7. 如图所示，直线AB ，CD 交于点O ，射线OM 平分AOC ∠．若38AOM ∠=︒，则BOC∠等于（ ）A ．104︒B ．144︒C ．106︒D ．136︒8. 如图，直线AB ，CD 相交于点O ，OE AB ⊥，垂足为点O ，若50BOD ∠=︒，则COE∠的度数为（ ）A ．40°B ．45°C ．50°D ．55°9. 下列结论中错误的是( )A ．连接两点的线段叫两点之间的距离B ．两点之间,线段最短C ．同角的补角相等D ．两点确定一条直线二、细心填一填10. 如图，两条直线AB ，CD 交于点O ，射线OM 是∠AOC 的平分线，若∠BOD ＝80°，则∠BOM 的度数是__．11. 如图是一把剪刀，若∠AOB+∠COD＝60°，则∠BOD＝____°．12. 如图，直线AB，CD相交于点O，∠EOC=70°，OA平分∠EOC，则∠BOD=________．13. 若∠α=70°，则它的补角是________．14. 如图，直线AB、CD相交于点O，OE平分∠BOD，若∠AOD-∠DOB＝60°，则∠EOB＝___.15. 已知，如图，直线AB、CD相交于O，OE平分∠BOD且∠AOE=150°，∠AOC的度数为______．16. 如图，直线AB、CD相交于点O，135∠=︒，则直线AB与直线CD的夹角是BOC______︒．17. 如图，直线AB和OC相交于点O，∠AOC=100°，则∠1=_______度．18. 如图，直线AB CD 、相交于O 点，OE AB ⊥．（1）2∠和3∠互为___角； 1∠和3∠互为_______角；2∠和4∠互为___角． （2）若125∠=︒，那么2∠=_________；3BOE ∠=∠-∠______=_______︒-____︒=___︒；4∠=∠_____1-∠=__︒-____︒=______︒．三、用心做一做19. 如图，直线AB 、CD 相交于点O ，DOE BOD ∠∠＝，OF 平分AOE ∠，20BOD ∠︒＝．（1）求AOE ∠的度数；（2）求COF ∠的度数．20. 如图所示，已知∠AOC=160°，OC 平分∠BOD ，OE 平分∠AOD ，求∠BOE 的度数．21. 如图，直线BC 与MN 相交于点O ，AO ⊥BC ，OE 平分∠BON ，若∠EON=20°．求∠AOM 和∠NOC 的度数．22. 如图，已知DM 平分ADC ∠，BM 平分ABC ∠，且27A ∠=︒，33M ∠=︒，求C ∠的度数.23. 已知O 为直线AB 上一点，射线OD 、OC 、OE 位于直线AB 上方，OD 在OE 的左侧，120AOC ∠=︒，DOE α∠=．（1）如图1，70α=︒，当OD 平分AOC ∠时，求EOB ∠的度数．（2）如图2，若2DOC AOD ∠=∠，且80α<︒，求EOB ∠（用α表示）． （3）若90α=︒，点F 在射线OB 上，若射线OF 绕点O 顺时针旋转n ︒（0180n <<︒），2FOA AOD ∠=∠，OH 平分EOC ∠，当120FOH ∠=︒时，求n 的值．24. 如图，要测得两堵墙形成的∠AOB 的度数，但人不能进入围墙，请你写出两种不同的测量方法，并说明几何道理．参考答案一、精心选一选1. D【分析】利用直线2l 不经过点M 可判断A ，利用点M 在直线1l 上，不在直线2l 上可判断B ，利用点M 在直线1l 外可判断C ，根据直线1l 与直线2l 相交，点M 在直线1l 上，直线2l 不经过点M 可判断D ．【详解】解：A ．直线2l 不经过点M ，故本选项不合题意；B ．点M 在直线1l 上，不在直线2l 上，故本选项不合题意；C ．点M 在直线1l 外，故本选项不合题意；D ．直线1l 与直线2l 相交，点M 在直线1l 上，直线2l 不经过点M ，故本选项符合题意；答案：D ．【点睛】本题考查根据语句画图问题，掌握画图的基本语句是解题关键． 2. B【分析】根据对顶角的定义对各图形判断即可．【详解】解：A 、∠1和∠2不是对顶角，故选项错误；B 、∠1和∠2是对顶角，故选项正确；C 、∠1和∠2不是对顶角，故选项错误；D 、∠1和∠2不是对顶角，故选项错误．故选B ．【点睛】本题考查了对顶角的定义，是基础题，熟记概念并准确识图是解题的关键． 3. B【分析】根据量角器的读数以及的对顶角相等即可求得α∠的度数．【详解】由图可知α∠的对顶角为60︒，根据对顶角相等，则α∠的度数为60︒， 故选B ．【点睛】本题考查了量角器的使用，对顶角相等，理解对顶角相等是解题的关键． 4. C【解析】【分析】根据对顶角的定义对各选项分析判断后利用排除法求解．【详解】A 、∠1和∠2不是对顶角，故A 错误；B 、∠1和∠2不是对顶角，故B 错误；C 、∠1和∠2是对顶角，故C 正确；D 、∠1和∠2不是对顶角，是邻补角，故D 错误．故选：C ．【点睛】本题考查了对顶角、邻补角，熟记概念并准确识图是解题的关键．5. C【解析】角平分线定义，对顶角的性质，补角的定义．由∠BOD=760，根据对顶角相等的性质，得∠AOC=760，根据补角的定义，得∠BOC=1040．由射线OM 平分∠AOD ，根据角平分线定义，∠COM=380．∴∠BOM=∠COM ＋∠BOC=1420．故选C ．6. B如图，直线AB、CD相交于一点O，图中的∠AOD和∠BOC，∠AOC和∠BOD 是对顶角，共计2对.故选B.7. A【分析】根据2∠的度数，利用平角的定义计算即可．∠=∠AOC AOM计算AOC【详解】∵OM平分AOC∠，38∠=︒，AOM∴∠=∠=⨯︒=︒，AOC AOM223876∴∠=︒-∠=︒-︒=︒．BOC AOC180********故选：A．【点睛】本题考查了角的平分线，平角的定义，熟记角的定义，平角的定义是解题的关键．8. A【分析】根据对顶角相等得到AOC∠的度数．∠，再根据作余角定义，求COE【详解】解：∵50⊥∠=∠=，OE ABAOC BOD︒∴90905040∠=︒-∠=︒-︒=︒，COE AOC故选：A．本题考查了对顶角的性质和互为余角的性质，熟悉相关性质并能进行计算是解题的关键．9. A【分析】根据两点之间的距离，同角的余角或补角相等，两点确定一条直线，线段的性质即可判断．【详解】解：A、连接两点的线段的长度叫两点之间的距离，故错误；B、两点之间，线段最短，故正确；C、同角的补角相等，故正确；D、两点确定一条直线，故正确；故选A．【点睛】本题考查了对余角或补角，直线的性质，线段的性质的理解和运用，知识点有：同角的余角或补角相等，两点确定一条直线，两点之间线段最短二、细心填一填10. 140°【分析】先根据对顶角相等得出∠AOC＝80°，再根据角平分线的定义得出∠COM，最后解答即可．【详解】解：∵∠BOD＝80°，∴∠AOC＝80°，∠COB＝100°，∵射线OM是∠AOC的平分线，∴∠COM＝40°，∴∠BOM＝40°+100°＝140°，故答案为：140°．【点睛】此题考查对顶角和角平分线的定义，关键是得出对顶角相等．11. 150【分析】根据对顶角相等得到∠AOB的度数，再根据邻补角的定义即可得出结论．【详解】∵∠AOB=∠COD，∠AOB＋∠COD=60°，∴∠AOB=∠COD=30°，∴∠BOD=180°－∠AOB=180°－30°=150°．故答案为150°．【点睛】本题考查了对顶角相等和邻补角的定义．求出∠AOB的度数是解题的关键．12. 35°【详解】试题分析：∵∠EOC＝70°，OA平分∠EOC，∴∠AOC＝12∠EOC＝12×70°＝35°，∴∠BOD＝∠AOC＝35°．故答案为35°．点睛：本题考查了角平分线的定义，对顶角相等的性质，熟记定义并准确识图是解题的关键．13. 110°．【详解】试题分析：根据定义∠α的补角度数是180°﹣70°=110°．故答案是110°．考点：余角和补角．14. 30°【详解】∵∠AOD－∠BOD＝60°,∴∠AOD=∠BOD+60°,∵AB为直线,∴∠AOD+∠BOD=∠AOB=180°,∴∠BOD+60°+∠BOD=180°,∴∠BOD=60°,∵OE平分∠BOD，∴∠EOB＝30°故答案为: 30°.15. 60°【解析】根据两直线相交，对顶角相等，可推出∠AOC=∠DOB，又根据OE平分∠BOD，x,∠AOE=150°，可求∠AOC．设∠AOC=x, ∠AOD=180°-x,∠DOE=12x，解：设∠AOC=x, ∠AOD=1800-x,∠AOC=∠DOB，OE平分∠BOD，∠DOE=12x=150°，x=60°, ∠AOC=60°∵∠AOE=150°，∴180°-x+ 12故答案为60°“点睛”本题主要考查对顶角的性质以及角平分线的定义，邻补角，解决问题的关键是用方程思想解题．16. 45【分析】先根据邻补角的定义求出∠AOC，再根据直线的夹角为锐角解答．【详解】解：∵∠BOC=135°，∴∠AOC=180°-∠BOC=180°-135°=45°，∴直线AB与直线CD的夹角是45°．故答案为：45．【点睛】本题考查了邻补角的定义，要注意直线的夹角是锐角．17. 80．【解析】试题分析：由邻补角互补，得∠1=180°﹣∠AOC=180°﹣100°=80°，故答案为80．考点：对顶角、邻补角．18. 余余邻补25 2 90 25 65 AOB180 25155根据余角、补角、邻补角、平角的定理计算求解即可．【详解】解：∵OE AB ⊥，∴90AOE EOB ==︒∠∠，∴2390=+︒∠∠，1390∠+∠=︒，∴2∠和3∠互为余角； 1∠和3∠互为余角；∵24180∠+∠=︒且有公共边，∴2∠和4∠互为邻补角；∵125∠=︒，1∠和2∠互为对顶角，∴1225∠=∠=︒，32BOE ∠=∠-∠=90︒-25︒=65︒；4∠=∠AOB 1-∠=180︒-25︒=155︒．故答案为：余；余；邻补；25︒；2；90；25；65；AOB ；180；25；155．【点睛】本题考查的是余角和补角、对顶角和邻补角的概念，如果两个角的和等于90°（直角），就说这两个角互为余角，如果两个角的和等于180°（平角），就说这两个角互为补角．三、用心做一做19. （1）140︒；（2）90︒【分析】（1）因为DOE BOD =∠，求出∠BOE ，得出AOE ∠；（2）利用180COF DOE EOF ∠=︒-∠-∠，从而求出COF ∠的度数．【详解】解：（1）20BOD ∠=︒，DOE BOD ∠=∠，202040BOE ∴∠=︒+︒=︒，18040140AOE ∴∠=︒-︒=︒；（2）20DOE ∠=︒，111407022EOF AOE ∠=∠=⨯︒=︒， 180207090COF ∴∠=︒-︒-︒=︒．本题考查了平角的性质、对顶角、角平分线的性质，解题的关键是根据题意得出各角之间的关系．20. 110°【分析】先利用平角的概念求出∠BOC的度数，然后利用角平分线的定义即可求出∠BOD的度数和∠EOD的度数，最后利用∠BOE=∠EOD+∠BOD即可求解．【详解】∵∠AOC=160°，∠AOC+∠BOC=180°，∴∠BOC=180°-160°=20°．∵OC平分∠BOD，∴∠BOD=2∠BOC=40°．又∵∠AOD+∠BOD=180°，∴∠AOD=180°-40°=140°．∵OE平分∠AOD，∴∠EOD=12∠AOD=70°，∴∠BOE=∠EOD+∠BOD=70°+40°=110°．【点睛】本题主要考查角平分线的定义，平角的定义和角的和与差，掌握角平分线的定义是解题的关键．21. 50AOM︒∠=，140NOC︒∠=.【解析】【分析】要求∠AOM的度数，可先求它的余角．由已知∠EON=20°，结合角平分线的概念，即可求得∠BON．再根据对顶角相等即可求得；要求∠NOC的度数，根据邻补角的定义即可.【详解】解：∵OE平分∠BON，∴∠BON=2∠EON=2×20°=40°，∴∠NOC=180°-∠BON=180°-40°=140°，∠MOC=∠BON=40°，∵AO ⊥BC ，∴∠AOC=90°，∴∠AOM=∠AOC-∠MOC=90°-40°=50°，所以∠NOC=140°，∠AOM=50°. 【点睛】结合图形找出各角之间的关系，利用角平分线的概念，邻补角的定义以及对顶角相等的性质进行计算.22. 39C ∠=︒.【分析】根据角平分线的性质及对顶角相等可求得，2C M A ∠=∠-∠，然后再利用已知条件及角的和差计算求解即可.【详解】解：如图所示：设BC 与MD 的交点为E DM 平分ADC ∠，BM 平分ABC ∠21CDQ ∴∠=∠，22ABQ ∠=∠在CDQ ∆与ABQ ∆中，CQD AQB ∠=∠2122C A ∴∠+∠=∠+∠①在CDE ∆与MBE ∆中，CED MEB ∠=∠12C M ∴∠+∠=∠+∠②用2⨯-②①得：2C M A ∠=∠-∠27A ∠=︒，33M ∠=︒2332739C ∴∠=⨯︒-︒=︒故39C∠=︒【点睛】角平分线的性质及对顶角相等、角的和差计算是本题的考点，根据题意求得2C M A∠=∠-∠是解题的关键.23. （1）50°；（2）140EOBα∠=︒-；（3）168或72．【分析】（1）利用角平分线的定义和邻补角的定义求得∠BOC和∠EOC，再利用角的和差即可求得∠BOE；（2）先根据已知数量关系求得∠DOE，再利用角的和差即可得出结论；（3）设BOF n∠=︒，分①若DOE∠在AOC∠的内部，②当DOE∠在射线OC的两侧时两种情况，利用角的和差列出方程求解即可．【详解】解：（1）∵120AOC∠=︒，OD平分AOC∠，∴60AOD DOC∠=∠=︒，60BOC∠=︒，又70DOEα∠==︒，∴706010COE∠=︒-︒=︒，∴6050BOE COE∠=︒-∠=︒；（2）∵120AOC∠=︒，2DOC AOD∠=∠，∴1403AOD AOC∠=∠=︒，80DOC∠=︒，60BOC∠=︒，∴80EOCα∠=︒-，∴6080140 EOB BOC EOCαα∠=∠+∠=︒+︒-=︒-；（3）①如图，若DOE∠在AOC∠的内部设BOF n∠=︒则依题意有：()11118090222AOD FOA n n ∠=∠=︒-︒=︒-︒， ∵120AOC ∠=︒，90DOE α∠==︒，∴1209030AOD EOC AOC DOE ∠+∠=∠-∠=︒-︒=︒，又∵OH 平分EOC ∠，∴()113022EOH EOC AOD ∠=∠=︒-∠111309030224n n ⎛⎫=︒-︒+︒=︒-︒ ⎪⎝⎭， 又120FOH ∠=︒，∴1118090903012024n n n ︒-︒+︒-︒+︒+︒-︒=︒，∴168n =；②当DOE ∠在射线OC 的两侧时如图设BOF n ∠=︒，则依题意有119022AOD AOF n ∠=∠=︒-︒，∵120AOC ∠=︒，90DOE α∠==︒，∴190120602COE AOD n ∠=∠+︒-︒=︒-︒，又OH 平分EOC ∠，∴113024EOH EOC n ∠=∠=︒-︒，又120FOH ∠=︒，∴1130909012042n n n ⎛⎫︒+︒-︒+︒-︒-︒=︒ ⎪⎝⎭， ∴72n =，∴综上所述OF 顺时针旋转的角度为168或72．【点睛】本题考查邻补角的有关计算，角平分线的有关计算，角的和差，一元一次方程的应用．（3）中能分类讨论画出图形，结合图形利用角的和差列出方程是解题关键．24. 见解析【分析】根据邻补角和对顶角的性质进行设计即可．【详解】方法一：如图所示，延长AO至C，测量∠BOC的度数，根据邻补角的性质得：∠AOB=180°-∠BOC，即可求解；方法二：如图所示，分别延长AO，BO，测量∠COD的度数，根据对顶角相等得：∠AOB=∠COD，即可求解．【点睛】本题考查邻补角和对顶角的实际应用，熟记基本定义和性质并灵活运用是解题关键．。

5.1.1 相交线姓名年级分数B有公共顶点且互补的两个角D有公共顶点且有一条公共边，另一边互为反向延长3•如图，直线AB与CD相交于点O ,若ZAOC+ZBOD=90° ,则ZBOC ()5•如果一个角比它的邻补角小30°,则这个角的度数为______ ° o6.如图，AB交CD于O点，OE是端点为O的一条射线，图中的对顶角有____ 对邻补角各有______ 对一、选择题1 •如图所示，Z1和Z2是对顶角的图形冇(A 135°B 120°C 100°D 145°4题图训是-----A和为180°的两个角C有一条公共边相等的两个角线的两个角ZAOC=80° , Zl=30°,求Z2 的度数 )&如图，直线AB、CD相交于点O,解：因为ZDOB=Z ______ ((己知)所以，ZDOB二__ ° (等量代换)=80°又因为ZI=30°( )所以Z2=Z ___ - Z _____ = ______ - ______ =____ °三、解答题：9.如图，直线AB, CD相交于点O , OE平分ZBOD, OF平分ZCOE, ZAOD： ZAOF的度数。

ZBOE=4:L 求F10.如图所示是某城市古建筑群中一座古塔底部的建筑平面图，请你利用学过的知识设计如何测量出古塔外墙底部的ZABC的大小的方案，并说明理由。

参考答案：1. A2.D3.A4.2 个ZACD ZB5.75°6. 2； 57.35°8. ZAOC,对顶角相等，ZAOC,8()° ,已知ZBOD, Z1, 80° , 30° , 50°9 解：由已知设ZAOD=4x° , ZBOE=x°VOE 平分ZBOD,・*. ZBOD=2ZBOE=2x°VZAOD+ZBOD=180°・\6x=180°x=30°・°・ ZBOE=30° ,・\ZAOD=120°ZBOD=60° ZCOE=150°VOF 平分ZCOE ・•・ ZEOF=- ZCOE=75°2・・・ Z BOF= ZEOF- ZBOE=450ZAOF=ZAOB-ZBOF=135°10.方法一：作AB的延长线，如图1所示，量出ZCBD的度数，ZABC=180° -ZCBD 方法二：作AB和CB的延长线，如图2所示，量I1IZDBE的度数，ZABC=ZDBE我的写字心得体会从小开始练习写字，几年来我认认真真地按老师的要求去练习写字。