伺服电机的推力计算公式

选择伺服电机时，首先要考虑的是功率的选择。

一般应注意以下两点：1．如果选择的电机功率太小，就会出现“小马车”现象，会导致电机长期过载，由于发热而损坏绝缘，甚至烧坏电机。

2．如果电动机功率太大，就会出现“大手拉车”现象，其输出机械功率不能得到充分利用，功率因数和效率不高，不仅不利于用户和电网。

而且还会造成电能浪费。

也就是说，电动机功率既不能太大也不能太小。

为了正确选择电动机功率，必须进行以下计算或比较：P = F * V / 100（其中p是计算出的功率，以KW为单位，f是所需的拉力，以n为单位，v是工作机的线速度m / s）另外，最常用的方法是通过类比选择电动机的功率。

所谓的类比法是比较类似生产机械中使用的电动机的功率。

具体方法是知道该装置或附近其他装置中类似生产机械使用了多少功率电动机，然后选择具有类似功率的电动机进行调试。

调试的目的是验证所选电动机是否与生产机械匹配。

验证方法是使电动机带动生产机械运转，用钳形电流表测量电动机的工作电流，并将测量的电流与电动机铭牌上标记的额定电流进行比较。

如果电动机的实际工作电流与标在脾脏上的额定电流相差不大，则表明所选电动机的功率合适。

如果电机的实际工作电流比铭牌上标明的额定电流低70％，则表明电机功率太大，应更换功率较小的电机。

如果测得的电动机工作电流比铭牌上标出的额定电流大40％以上，则表明电动机功率过小，应更换功率较大的电动机。

实际上，它应该是考虑转矩（转矩），电动机功率和转矩的计算公式。

T ＝9550p / n。

其中：P功率，kw；N-电机额定转速，r / min；T扭矩，Nm。

电动机的输出扭矩必须大于工作机械所需的扭矩，并且通常需要安全系数。

机械功率公式：P = T * N / 97500P：功率单位W；T：扭矩，g / cm；N：转速，以r / min为单位。

伺服电机选型计算公式伺服电机选型计算公式是指通过一系列的计算公式来确定伺服电机的合适参数，以满足特定需求。

伺服电机选型的主要目标是确定伺服电机的额定转矩、额定电流、额定功率等参数，以及选择合适的伺服驱动器。

下面将介绍一些常用的伺服电机选型计算公式。

1.负载的转矩计算公式：负载的转矩是伺服电机选型的基础，通过计算负载的转矩，可以确定伺服电机的额定转矩。

负载的转矩可以通过以下公式计算：负载转矩=（负载力*负载半径）/（传动效率*减速比）2.伺服电机的额定转矩计算公式：伺服电机的额定转矩是指在额定转速下，电机能够提供的最大转矩。

额定转矩可以通过以下公式计算：额定转矩=（负载转矩+加速扭矩）/传动效率3.伺服电机的额定电流计算公式：伺服电机的额定电流是指在额定转矩下，电机所需的额定电流。

额定电流可以通过以下公式计算：额定电流=额定转矩*电流系数/额定转速4.伺服电机的额定功率计算公式：伺服电机的额定功率是指在额定转矩和额定转速下，电机所提供的对外功率。

额定功率可以通过以下公式计算：额定功率=额定转矩*额定转速/9.555.伺服驱动器的额定功率计算公式：伺服驱动器的额定功率是指驱动器所能提供的最大功率。

额定功率可以通过以下公式计算：额定功率=伺服电机的额定功率/驱动器的效率除了上述几个常用的伺服电机选型计算公式外，还需要考虑一些其他因素，例如：负载的加速时间、负载的惯性矩、伺服系统的控制精度等，这些因素都会对伺服电机的选型产生影响，需要综合考虑。

同时，还需要根据具体的应用环境和需求，选择合适的伺服电机和驱动器型号，以确保系统的性能和可靠性。

需要注意的是，伺服电机选型计算公式只是一个参考，实际选型过程中还需要考虑一系列的工程参数和实际情况，同时也需要借助一些专业的伺服电机选型软件，以更准确地确定伺服电机的参数。

伺服电机功率扭矩计算案例
咱来个伺服电机功率扭矩计算的案例哈。

比如说，有个小机器人，它要举起一个5千克的小方块，这个小方块呢，得被举高1米，而且要在2秒内完成这个动作。

首先呢，我们得算出这个小机器人做的功。

功的公式是W = F × s，这里的F就是力，小方块的重力就是这个力啦，根据重力公式G = mg（m是质量，g取10牛/千克），那这个小方块的重力G = 5 × 10 = 50牛。

s就是距离，这里是1米，所以做的功W = 50 × 1 = 50焦耳。

然后呢，功率的公式是P=(W)/(t)，W是功，我们刚算出来是50焦耳，t是时间，是2秒，那功率P=(50)/(2)=25瓦。

这就是这个小机器人举小方块这个动作需要的功率啦。

再来说说扭矩。

假设这个小机器人的手臂长0.5米，我们要让小方块转起来（就像拧瓶盖那样的转动，不过这里是举起来的同时转一下这个概念哈）。

扭矩的公式是T = F × r，F还是那个重力50牛，r就是手臂的长度0.5米，那扭矩T = 50 × 0.5 = 25牛·米。

所以呀，对于这个小机器人举小方块的这个事儿，功率大概需要25瓦，扭矩大概是25牛·米，这样我们就可以根据这些数据去选合适的伺服电机啦，就像给小机器人找个刚好能干活的大力士伙伴一样呢。

伺服电动缸推力计算公式例题伺服电动缸（也称线性伺服电机）是一种电动缸，它将线性运动转化为旋转运动，并利用电机控制系统实现精确的推力调节。

在伺服电动缸的设计和应用中，常常需要计算电动缸的推力，以确定其满足需求的能力。

推力计算公式:推力（N）= 力矩（N·m）/ 力臂（m）力矩（N·m）= 力（N） ×距离（m）力臂（m）= 力点到旋转中心的距离（m）例题：某伺服电动缸对应用场景的要求是需提供2000N的推力。

现给定伺服电动缸的力臂为0.2m，求该伺服电动缸所需的力矩。

解答：根据推力计算公式可知，推力（N）= 力矩（N·m）/ 力臂（m）。

已知推力为2000N，力臂为0.2m，代入计算公式得到：2000N = 力矩（N·m）/ 0.2m。

将公式变形，得到力矩：力矩（N·m）= 推力（N） ×力臂（m）= 2000N × 0.2m = 400N·m。

所以，该伺服电动缸所需的力矩为400N·m。

以上例题给出了伺服电动缸推力计算的具体计算过程。

力矩和力臂的概念非常重要，力矩表示力在转动时产生的力矩大小，力臂是力点到旋转中心的垂直距离。

通过理解和应用这些概念，可以准确计算伺服电动缸的推力。

在实际应用中，伺服电动缸的推力计算还需要考虑一些其他因素，如摩擦力、负载惯性、系统误差等。

这些因素可能会对伺服电动缸的推力产生影响，需要在计算中进行综合考虑。

伺服电动缸的推力计算公式是应用伺服电动缸时进行设计和选择的重要参考内容之一。

准确计算推力可以帮助确保伺服电动缸满足需求，并为系统的设计提供重要的参考依据。

在实际应用中，还需要结合具体的系统要求和实际情况进行综合考虑，以确保伺服电动缸的性能和可靠性。

伺服扭力的计算公式为多少伺服扭力是伺服电机在工作时产生的扭矩，它是伺服系统中一个重要的参数。

在工程设计中，计算伺服扭力是非常重要的，因为它直接影响到伺服电机的选型和系统的稳定性。

在本文中，我们将介绍伺服扭力的计算公式以及如何应用这些公式进行工程设计。

伺服扭力的计算公式可以根据伺服电机的工作原理和系统的参数来推导。

一般来说，伺服电机的扭矩可以通过以下公式来计算：T = I α + T_load。

其中，T是伺服电机的输出扭矩，I是伺服电机的转动惯量，α是伺服电机的角加速度，T_load是外部载荷对伺服电机的负载扭矩。

转动惯量I是伺服电机旋转惯量的一个重要参数，它可以通过下面的公式来计算：I = m r^2。

其中，m是伺服电机的质量，r是伺服电机的半径。

通过这个公式，我们可以看到伺服电机的转动惯量与其质量和尺寸有关，因此在设计伺服系统时需要考虑伺服电机的质量和尺寸对其转动惯量的影响。

角加速度α是伺服电机旋转加速度的一个重要参数，它可以通过下面的公式来计算：α = (ω_f ω_i) / t。

其中，ω_f是伺服电机的最终角速度，ω_i是伺服电机的初始角速度，t是伺服电机的加速时间。

通过这个公式，我们可以看到伺服电机的角加速度与其角速度的变化率和加速时间有关，因此在设计伺服系统时需要考虑伺服电机的加速度对其扭矩的影响。

外部载荷对伺服电机的负载扭矩T_load是伺服系统中另一个重要的参数，它可以通过下面的公式来计算：T_load = F r。

其中，F是外部载荷的力，r是伺服电机的半径。

通过这个公式，我们可以看到外部载荷对伺服电机的负载扭矩与外部载荷的力和伺服电机的尺寸有关，因此在设计伺服系统时需要考虑外部载荷对伺服电机扭矩的影响。

综上所述，伺服扭力的计算公式可以通过转动惯量、角加速度和外部载荷对伺服电机的负载扭矩来推导。

在实际工程设计中，我们可以通过这些公式来计算伺服扭力，从而选择合适的伺服电机和优化系统参数，以满足工程需求并提高系统的稳定性和性能。

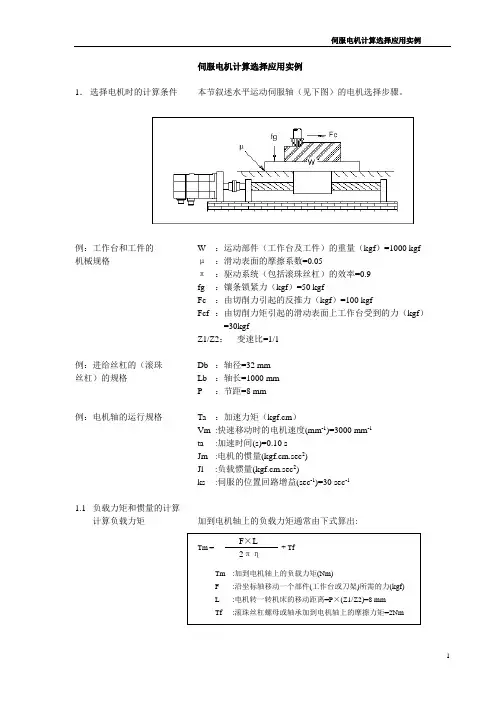
伺服电机计算选择应用实例1． 选择电机时的计算条件 本节叙述水平运动伺服轴（见下图）的电机选择步骤。

例：工作台和工件的W ：运动部件（工作台及工件）的重量（kgf ）=1000 kgf 机械规格 μ ：滑动表面的摩擦系数=0.05π ：驱动系统（包括滚珠丝杠）的效率=0.9 fg ：镶条锁紧力（kgf ）=50 kgfFc ：由切削力引起的反推力（kgf ）=100 kgfFcf：由切削力矩引起的滑动表面上工作台受到的力（kgf ） =30kgfZ1/Z2： 变速比=1/1例：进给丝杠的（滚珠 Db ：轴径=32 mm 丝杠）的规格 Lb ：轴长=1000 mm P ：节距=8 mm例：电机轴的运行规格 Ta ：加速力矩（kgf.cm ）Vm :快速移动时的电机速度(mm -1)=3000 mm -1 ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec 2) Jl :负载惯量(kgf.cm.sec 2)ks :伺服的位置回路增益(sec -1)=30 sec -11.1 负载力矩和惯量的计算 计算负载力矩 加到电机轴上的负载力矩通常由下式算出:Tm = + Tf Tm :加到电机轴上的负载力矩(Nm) F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf) L :电机转一转机床的移动距离=P ×(Z1/Z2)=8 mmTf:滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2NmF ×L2πη无论是否在切削，是垂直轴还是水平轴，F值取决于工作台的重量，摩擦系数。

若坐标轴是垂直轴，F值还与平衡锤有关。

对于水平工作台，F值可按下列公式计算：不切削时：F = μ（W+fg）例如：F=0.05×(1000+50)=52.5 (kgf)Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf)例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1，应根据数据单选择电机，其负载力矩在不切削时应大于0.9（Nm），最高转速应高于3000（min-1）。

伺服电机速度计算公式
理想情况下的速度计算公式：
在理想情况下，我们可以使用基本的物理公式来计算伺服电机的速度。

假设伺服电机的旋转惯量为J，电机所受的扭矩为T，则速度可以通过以
下公式计算：
ω=(T/J)*t
其中，ω表示电机的角速度，T表示电机所受的扭矩，J表示电机的
旋转惯量，t表示时间。

实际情况下考虑摩擦和负载的速度计算公式：
在实际情况下，我们需要考虑到伺服电机所受的摩擦和负载。

假设伺
服电机受到摩擦力 Ff、负载力 Fload 和外部负载扭矩 Mload 的作用，
则速度可以通过以下公式计算：
(T - Ff*d - Fload*d)/J = α
其中，α表示电机的角加速度，d表示电机旋转的角位移。

通过积分我们可以得到速度与时间的关系：
ω=ω0+α*t
其中，ω0表示初始速度。

同时，我们还可以将电机的加速度和速度的关系推导为：
a=α*r
其中，a表示电机的线加速度，r表示负载半径。

综上所述，实际情况下考虑摩擦和负载的速度计算公式可以表示为：ω = (T - Ff * d - Fload * d) / J * t + ω0
在实际应用中，以上的速度计算公式可能需要根据具体的情况进行微调和修正，但这些公式提供了基本计算速度的方法和思路。

电机的选择：（1）电机扭矩的计算 负载扭矩是由于驱动系统的摩擦力和切削力所引起的可用下式表达： FL M =π2式中 M-----电动机轴转距；F------使机械部件沿直线方向移动所需的力；L------电动机转一圈（2πrad ）时，机械移动的距离2πM 是电动机以扭矩M 转一圈时电动机所作的功，而FL 是以F 力机械移动L 距离时所需的机械功。

实际机床上，由于存在传动效率和摩擦系数因素，滚珠丝杠克服外部载荷P 做等速运动所需力矩，应按下式计算：z z M h h F M B spSPao P K 211122⎪⎪⎭⎫ ⎝⎛++=ηππ M 1-----等速运动时的驱动力矩(N.mm)π2hF spao K---双螺母滚珠丝杠的预紧力矩(N.mm) Fao------预紧力(N),通常预紧力取最大轴向工作载荷Fm ax的1/3，即F ao =31F m ax当F m ax 难于计算时，可采用F ao =(0.1~0.12))(N C a ； C a -----滚珠丝杠副的额定载荷，产品样本中可查：hsp-----丝杠导程(mm)；K--------滚珠丝杠预紧力矩系数，取0.1~0.2；P---------加在丝杠轴向的外部载荷(N),W F P μ+=； F---------作用于丝杠轴向的切削力(N)； W--------法向载荷(N),P W W 11+=；W 1-----移动部件重力(N),包括最大承载重力；P 1-------有夹板夹持时（如主轴箱）的夹板夹持力；μ --------导轨摩擦系数，粘贴聚四氟乙烯板的滑动导轨副09.0=μ，有润滑条件时，05.0~03.0=μ，直线滚动导轨004.0~003.0=μ；η1-------滚珠丝杠的效率，取0.90~0.95；MB----支撑轴承的摩擦力矩，即叫启动力矩(N.m),可以从滚珠丝杠专用轴承样本中得到，见表2-6（这里注意，双支撑轴承有M B 之和的问题）z 1--------齿轮1的齿数 z2--------齿轮2的齿数最后按满足下式的条件选择伺服电机M M s ≤1Ms-----伺服电机的额定转距（2）惯量匹配计算 为使伺服进给系统的进给执行部件具有快速相应能力，必须选用加速能力大的电动机，亦即能够快速响应的电机（如采用大惯量伺服电机），但又不能盲目追求大惯量，否则由于不能从分发挥其加速能力，会不经济的。

伺服传动的选型计算案例1：丝杠直线传动已知条件（负载质量m=5KG，丝杠传动导程p=10mm，工位移载行程s=1000mm，移载所需时间2.2s）据上述要求旋转一款合适的伺服电机。

解析：1. 首先一般伺服电机的额定转速为n=3000转，运动过程可视为恒扭矩传动∴丝杠传动的最快直线速度ν=3000x0.01=0.5 m/s加减速过程的速度变化图为了方便计算，可设定减速与减速时间相等均为t，最终匀速为0.5m/s∴s=1at2x2+0.5(2.2−2t)=1m2∴可得：1.1−0.5t=1得t=0.2s，则a=2.5 m/s22.根据需要的加速度可推算所需要的丝杠的轴向推力，从而推算出所需的扭矩已知负载质量：M=5kg，且经上推算的加速度a=4 m/s2(暂定)根据 F=m.a=5x2.5=12.5N（F为丝杠轴向推力）还可以根据丝杠传动电机扭矩与轴向力之间转换关系：T∗2∗π∗η=F∗p（T为电机扭矩，η为效率可取0.9）T=FP2πη=12.5x0.015.652= 0.0221 Nm3.根据需要出的扭矩再反推出所需电机的功率：∴根据功率扭矩之间的转换公式：T=9550∗pn反推得出P=T∗n9550=0.0221x30009550=0.00695 kw=6.95w从扭矩的角度100W以下的伺服电机都能满足要求4.伺服电机是精确定位的马达，不能只满足驱动扭矩，还需从惯量上去校核够不够, (丝杠φ15，长度1100)：丝杠传动系的惯量：J=J1负载+J2丝杠（可得其惯量0.426 x10−4 kg m2)J1=m∗r2=5x(p2π)2=5x(0.159）210−4 kg m2=0.1267x10−4 kg m2∴ J=（0.426+0.1267）x10−4 kg m2=0.5527 x10−4 kg m2所以可得总负载的惯量为0.5527 x10−4 kg m25.电机所需承受的总惯量已得知，则需要查询所选电机的惯量参数，这里以三菱电机为例由三菱电机属性的惯量匹配比为15~25，则可得：J电机=0.552720=0.0276∴可得100W的电机惯量太小，尽管扭矩够了，但是不能很精准地控制负载的定位所以应该选用HF-MP23G1(K9020)案例2：同步带直线传动已知条件（负载质量m=5KG，同步带轮直径d=50mm，工位移载行程s=1000mm，移载所需时间2s）据上述要求旋转一款合适的伺服电机。

手把手教你计算伺服电动缸的推力大小！
在选购伺服电动缸的时候，很多人都会对推力大小有要求，毕竟推力大小的不同，价格也不一样。

一般来说，伺服电动缸的推力越大，价格也越贵。

想要节约成本，选购合适推力大小的伺服电动缸是关键。

那么，怎么计算伺服电动缸的额定推力呢?下面森拓就跟大家来聊一聊这个问题。

伺服电动缸额定推力计算
1、额定推力(KN)=电机额定扭矩(N/M)x丝杆传动系数(5338或3.14)÷丝杆导程*减速比。

2、额定速度(MM/S)=电机额定速度÷60x丝杆导程÷减速比。

3、电动缸的实际推力:要按额定推力的85%来计算。

(另15%为电动缸配件配合的摩擦力。

4、在选择减速机型号时我们还要计算减速机的额定扭矩能否承受电动缸的额定推拉力。

(KN)。

伺服电机计算选择应用实例1． 选择电机时的计算条件 本节叙述水平运动伺服轴（见下图）的电机选择步骤。

例：工作台和工件的W ：运动部件（工作台及工件）的重量（kgf ）=1000 kgf 机械规格 μ ：滑动表面的摩擦系数=0.05π ：驱动系统（包括滚珠丝杠）的效率=0.9 fg ：镶条锁紧力（kgf ）=50 kgfFc ：由切削力引起的反推力（kgf ）=100 kgfFcf：由切削力矩引起的滑动表面上工作台受到的力（kgf ） =30kgfZ1/Z2： 变速比=1/1例：进给丝杠的（滚珠 Db ：轴径=32 mm 丝杠）的规格 Lb ：轴长=1000 mm P ：节距=8 mm例：电机轴的运行规格 Ta ：加速力矩（kgf.cm ）Vm :快速移动时的电机速度(mm -1)=3000 mm -1 ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec 2) Jl :负载惯量(kgf.cm.sec 2)ks :伺服的位置回路增益(sec -1)=30 sec -11.1 负载力矩和惯量的计算 计算负载力矩 加到电机轴上的负载力矩通常由下式算出:Tm = + Tf Tm :加到电机轴上的负载力矩(Nm) F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf) L :电机转一转机床的移动距离=P ×(Z1/Z2)=8 mmTf:滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2NmF ×L2πη无论是否在切削，是垂直轴还是水平轴，F值取决于工作台的重量，摩擦系数。

若坐标轴是垂直轴，F值还与平衡锤有关。

对于水平工作台，F值可按下列公式计算：不切削时：F = μ（W+fg）例如：F=0.05×(1000+50)=52.5 (kgf)(52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)=Tm= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf)例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1，应根据数据单选择电机，其负载力矩在不切削时应大于0.9（Nm），最高转速应高于3000（min-1）。

伺服电机功率电压计算公式
伺服电机是一种能够精确控制位置、速度和加速度的电动机，通常用于需要精
密控制的工业设备和机械。

在使用伺服电机时，我们需要了解其功率和电压之间的关系，以便正确选择电机和电源。

伺服电机的功率和电压之间的关系可以通过以下公式来计算：
P = V I。

其中，P代表功率（单位为瓦特），V代表电压（单位为伏特），I代表电流（单位为安培）。

根据这个公式，我们可以通过电压和电流来计算伺服电机的功率。

在实际应用中，通常会根据伺服电机的额定电压和额定电流来计算其额定功率。

额定电压是指电机设计时所使用的电压，而额定电流是指在额定电压下电机所消耗的电流。

通过这两个参数，我们可以计算出伺服电机的额定功率，从而为选择合适的电源提供参考。

除了额定功率外，我们还需要考虑伺服电机在工作过程中的实际功率需求。

在
某些情况下，伺服电机可能需要更高的功率来应对突发的负载变化或加速度要求。

因此，我们需要根据实际工作需求来选择合适的电源，以确保伺服电机能够正常工作并具有足够的性能储备。

另外，还需要注意的是，伺服电机在启动和停止过程中可能会产生较大的电流
冲击，因此电源系统需要具备一定的过载保护和稳压功能，以确保电机和电源的安全稳定运行。

总之，伺服电机的功率和电压之间的关系是一个重要的参数，对于正确选择电
机和电源具有重要意义。

通过上述公式和相关考虑，可以帮助我们更好地理解伺服电机的功率需求，并为实际应用提供参考依据。

伺服电机的推力计算公式伺服电机是一种能够根据外界的控制信号来控制转动位置和速度的电机。

在实际应用中，常常需要计算伺服电机的推力，以便确定其在特定工况下的使用能力和安全性。

本文将介绍伺服电机推力的计算公式及其相关内容。

一、伺服电机推力的计算公式伺服电机的推力计算公式如下：推力 = 力矩 / 半径其中，力矩是伺服电机产生的力矩，单位为牛顿·米（N·m）；半径是力矩作用的杠杆臂长度，单位为米（m）。

通过这个公式，我们可以根据伺服电机的力矩和杠杆臂长度来计算其推力。

二、伺服电机推力计算的应用伺服电机推力的计算在工程实践中具有重要的应用价值。

首先，推力的计算可以帮助工程师确定伺服电机的负载能力。

通过计算推力，工程师可以了解伺服电机在承受特定负载时所产生的力量，从而判断其是否能够满足实际工作需求。

其次，推力的计算还可以用于伺服电机的选型。

不同的应用场景对伺服电机的推力要求不同，通过计算推力，可以选择适合的伺服电机型号，以确保系统的正常运行和安全性。

三、推力计算的注意事项在进行伺服电机推力计算时，需要注意以下几点：1. 力矩的计算：力矩是伺服电机产生的力矩，可以通过电机的额定转矩和减速器的减速比进行计算。

在实际应用中，还需要考虑到负载的惯性矩和摩擦力矩等因素。

2. 杠杆臂的选择：杠杆臂是力矩作用的长度，一般选择负载到伺服电机轴线的距离。

在选择杠杆臂时，需要考虑到负载的重心位置、力矩的传递效率等因素。

3. 单位的统一：在进行推力计算时，需要保证所有的参数单位统一。

一般情况下，力矩的单位为牛顿·米（N·m），杠杆臂的单位为米（m），推力的单位为牛顿（N）。

如果参数单位不一致，会导致计算结果产生误差。

四、伺服电机推力计算的实例为了更好地理解伺服电机推力的计算方法，我们举一个实际应用的例子。

假设我们需要计算一台伺服电机在给定负载下的推力。

我们需要确定伺服电机的力矩。

假设该电机的额定转矩为10 N·m，减速比为10：1。

伺服电机丝杆推力计算公式伺服电机丝杆推力的计算可不是一件简单的事儿，它涉及到不少的物理知识和数学公式。

咱们先来说说啥是伺服电机丝杆。

想象一下，有一根长长的杆子，就像一根特别精细的金箍棒，而这个“金箍棒”能够在伺服电机的驱动下，非常精确地前后移动。

那这个推动它移动的力量，就是咱们要算的推力啦。

那怎么算这个推力呢？这就得用到一些公式了。

一般来说，推力（F）等于丝杆的导程（P）乘以螺距（L）乘以效率（η）再乘以扭矩（T）。

这里面每个量都有它的讲究。

导程呢，就好比是这根“金箍棒”上的刻度，比如说每转一圈它能前进 5 毫米，那这 5 毫米就是导程。

螺距呢，是丝杆上相邻两个螺纹之间的距离。

效率呢，是因为在传动过程中会有能量损失，不是所有的力都能完全用上。

扭矩就像是电机的“力气”，电机转得越用力，扭矩就越大。

给您举个例子吧，我之前在一个工厂里看到师傅们在调试一台新的机器。

这台机器就是靠伺服电机丝杆来控制一个部件的移动。

当时师傅们就一直在讨论怎么计算这个推力，才能让这个部件移动得既精准又有力。

他们拿着图纸，对着各种参数，一边计算一边调试。

我在旁边看着，感觉这真不是一件容易的事儿。

比如说，他们要考虑到这个部件的重量，如果推力不够大，部件就动不起来；要是推力太大了，又可能会损坏机器。

而且还要考虑到速度，如果想要部件移动得快，推力就得更大。

他们在那反复测量、计算，还不断地调整电机的参数，就为了找到那个最合适的推力。

回到咱们的计算公式，在实际应用中，还得考虑很多其他因素。

比如摩擦系数，因为部件在移动的时候会和其他东西产生摩擦，这会消耗一部分推力。

还有温度的影响，温度高了或者低了，材料的性能可能会变化，从而影响到推力的大小。

另外，不同类型的丝杆，它的计算公式可能还会有一些细微的差别。

比如说滚珠丝杆和梯形丝杆，它们的效率就不太一样，计算的时候就得特别注意。

总之，伺服电机丝杆推力的计算是个挺复杂但又特别重要的事儿。

只有算准了，才能让机器正常、高效地工作。