江苏省东海高级中学行知部2016-2017学年高一上学期第三次学分认定(月考)数学试题Word版含答案

江苏省连云港市东海高级中学【精品】高一上学期第一次月考数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知集合{}1,3,5,7A =，{}2,3,4,5B =，则AB = A ．{}3 B ．{}5C ．{}3,5D ．{}1,2,3,4,5,7 2．已知集合{}220A x x x =-->，则A =R A ．{}12x x -<<B ．{}12x x -≤≤C ．}{}{|12x x x x <-⋃D ．}{}{|1|2x x x x ≤-⋃≥ 3．已知集合(){}22,1,,A x y x y x Z y Z =+≤∈∈，则A 的子集个数为（ ） A ．32 B ．31C ．16D ．5 4．下列各组函数中，表示同一函数的是（ ）．A ．()1f x =，()0g x x =B ．()2f x x =+，()242x g x x -=- C ．()f x x =，()g x =D ．()f x x =，()2g x = 5．若一系列的函数解析式相同，值域相同但定义域不同，则称这些函数为“孪生函数”．那么函数解析式为221y x =+，值域为{}3,19的“孪生函数”共有 ( )A ．15个B ．12个C ．9个D ．8个6．设()()21141x x f x x ⎧+<⎪=⎨≥⎪⎩则使得()1f m =成立的m 值是 ( ) A ．10B ．0，10C ．1，﹣1，11D ．0，﹣2，10 7．若函数()()2212f x x a x =-+-+在(),4-∞上是增函数，则实数a 的取值范围是（ ）A ．5a ≥B ．5a =C ．5a >D ．5a < 8．若函数21()242=-+f x x x 的定义域、值域都是[2,2]b ，则（ ） A ．2b = B ．[1,2]b ∈ C ．(1,2)b ∈ D ．1b =或2b = 9．奇函数f(x)在(),0∞-上的解析式是f(x)=x （1+x ），则f(x)在()0,∞+上有（ ）A ．最大值-1/4B ．最大值1/4C ．最小值-1/4D ．最小值1/410．已知()14212ax x f x a x x >⎧⎪=⎨⎛⎫-+≤ ⎪⎪⎝⎭⎩是R 上的单调递增函数,则实数a 的取值范围是 ( )A ．[)4,8B ．()0,8C ．()4,8D ．(]0,8 11．设二次函数()22f x ax ax c =-+在区间[]0,1上单调递减，且()()0f m f ≤，则实数m 的取值范围是( )A ．(－∞，0]B ．[2，＋∞)C ．(－∞，0]∪[2，＋∞)D ．[0，2] 12．已知奇函数()g x 是R 上的减函数,且()()2f x g x =+,若()(2)4f m f m +->,则实数m 的取值范围是( )A ．(,1)-∞B ．(,3)-∞C ．(1,)+∞D ．(3,)+∞二、填空题 13．设函数()2,166,1x x f x x x x ⎧≤⎪=⎨+->⎪⎩，则()()2f f -=________. 14．已知1(1)252f x x -=-，且()7f a =，则a 的值为__________．15．已知集合{}{},,1,2,3a b c =，且下列三个关系：①3a ≠；②3b =；③1c ≠，有且只有一个正确，则10010a b c ++=_________.16．已知()f x 是定义在R 上的偶函数，且当0x ≥时，()31x f x x -=+，若对任意实数1,22t ⎡⎤∈⎢⎥⎣⎦，都有()()20f t a f t +-->恒成立，则实数a 的取值范围是________.三、解答题17．设全集U=R ，集合A={x|1≤x ＜4}，B={x|2a≤x ＜3-a}．（1）若a=-2，求B∩A ，B∩(∁U A)；（2）若A∪B=A ，求实数a 的取值范围．18．计算：（1）()212103341301682--⎛⎫--++- ⎪⎝⎭； （2）11223x x -+=，求1x x -+及1122x x --．19．已知2()2(01)f x ax x x =-≤≤，求()f x 的最小值.20．经市场调查，某门市部的一种小商品在过去的20天内的日销售量（件）与价格（元）均为时间t （天）的函数，且日销售量近似满足函数()802=-g t t （件），而且销售价格近似满足于115(010)2()125(1020)2t t f t t t ⎧+≤≤⎪⎪=⎨⎪-<≤⎪⎩（元）． （1）试写出该种商品的日销售额y 与时间(0t 20)t ≤≤的函数表达式；（2）求该种商品的日销售额y 的最大值与最小值．21．函数()21ax b f x x +=+为R 上的奇函数，且1225f ⎛⎫= ⎪⎝⎭． (1)求函数()f x 的解析式；(2)若()235f x m ≤-区间[]2,4恒成立，求m 的取值范围． 22．已知函数4(),[1,2]f x x x x =-∈. （1）求函数()f x 的值域；（2）设22164()2()F x x a x x x=+--，[1,2]x ∈，a R ∈，求函数()F x 的最小值()g a ； （3）对（2）中的()g a ，若不等式2()24g a a at >-++对于任意的(3,0)a ∈-时恒成立，求实数t 的取值范围.参考答案1．C【解析】分析：根据集合{}{}1,3,5,7,2,3,4,5A B ==可直接求解{3,5}AB =. 详解：{1,3,5,7},{2,3,4,5}A B ==,{3,5}A B ∴⋂=,故选C点睛：集合题也是每年高考的必考内容，一般以客观题形式出现，一般解决此类问题时要先将参与运算的集合化为最简形式，如果是“离散型”集合可采用Venn 图法解决，若是“连续型”集合则可借助不等式进行运算.2．B【解析】分析：首先利用一元二次不等式的解法，求出220x x -->的解集，从而求得集合A ，之后根据集合补集中元素的特征，求得结果.详解：解不等式220x x -->得12x x <->或，所以{}|12A x x x =<->或，所以可以求得{}|12R C A x x =-≤≤，故选B.点睛：该题考查的是有关一元二次不等式的解法以及集合的补集的求解问题，在解题的过程中，需要明确一元二次不等式的解集的形式以及补集中元素的特征，从而求得结果. 3．A【分析】利用列举法表示集合A ，可得出集合A 中的元素个数，然后利用子集个数公式可得出集合A 的子集个数.【详解】 (){}()()()()(){}22,1,,0,0,1,0,0,1,1,0,0,1A x y x y x Z y Z =+≤∈∈=--， 则集合A 中有5个元素，因此，集合A 的子集个数为5232=.故选：A.本题考查有限集子集个数的计算，解题的关键就是确定出集合的元素个数，考查计算能力，属于基础题.4．C【分析】对选项逐一分析函数的定义域、值域和对应关系，由此判断出正确选项.【详解】对于A 选项，函数()f x 的定义域为R ，函数()g x 的定义域为{}|0x x ≠，故不是同一函数.对于B 选项，函数()f x 的定义域为R ，函数()g x 的定义域为{}|2x x ≠，故不是同一函数. 对于C 选项，函数()f x 的定义域为R ，函数()g x 的定义域为R ，且()()g x x f x ==，故是同一函数.对于D 选项，函数()f x 的定义域为R ，函数()g x 的定义域为{}|0x x ≥，故不是同一函数.故选：C【点睛】本小题主要考查两个函数是否是同一函数的判断，考查函数的定义域、值域和对应关系，属于基础题.5．C【解析】试题分析：由y=2x 2+1=3，得x 2=1，即x=1或x=-1，由y=2x 2+1=19，得x 2=9，即x=3或x=-3，即定义域内-1和1至少有一个，有3种结果，-3和3至少有一个，有3种结果，∴共有3×3=9种，故选C ．考点：1．函数的定义域及其求法；2．函数的值域；3．函数解析式的求解及常用方法． 6．D【分析】因为是分段函数，所以分：当m ＜1时，f （m ）=（m +1）2=1和当m ≥1时，f （m ）=4=1两种情况取并集．当m ＜1时，f （m ）=（m +1）2=1∴m=﹣2或m=0当m ≥1时，f （m ）=4∴m=10综上：m 的取值为：﹣2，0，10故选D ．【点睛】本题主要考查分段函数的应用，主要涉及了已知函数值求自变量，同时，还考查了分类讨论思想和运算能力，属中档题．7．A【分析】分析二次函数()y f x =图象的开口方向和对称轴，结合题意可得出14a -≥，解出即可.【详解】由于二次函数()()2212f x x a x =-+-+图象开口向下，对称轴为直线1x a =-. 由于该函数在区间(),4-∞上是增函数，则14a -≥，解得5a ≥.因此，实数a 的取值范围是5a ≥.故选：A.【点睛】本题考查利用二次函数在区间上的单调性求参数，要结合二次函数图象的开口方向与对称轴进行分析，考查分析问题和解决问题的能力，属于基础题.8．A【解析】由题意得，函数()21242f x x x =-+图象的对称轴为2x =， ∴函数()f x 在区间[]2,2b 上单调递增，且定义域、值域都是[]2,2b ，∴()222442f b b b b =-+=，即2320b b -+=， 解得2b =或1b =（舍去）∴2b =．选A ．9．B【分析】先根据奇函数性质求f(x)在()0,∞+上解析式，再根据二次函数性质求最值.【详解】当0x >时，2111()()[(1)](1)()244f x f x x x x x x =--=---=-=--+≤， 所以当12x =时，()f x 取最大值14，选B. 【点睛】已知函数的奇偶性求函数解析式，主要抓住奇偶性讨论函数在各个区间上的解析式，或充分利用奇偶性得出关于()f x 的方程，从而可得()f x 的解析式.10．A【分析】由条件利用函数的单调性的性质可得4﹣2a ＞0，且a ＞0，且 4﹣2a +2≤a ，由此求得实数a 的取值范围．【详解】 根据f （x ）=42121a x x ax x ⎧⎛⎫-+≤⎪ ⎪⎝⎭⎨⎪⎩，，＞是R 上的单调递增函数，可得4﹣2a ＞0，且a ＞0，且 4﹣2a +2≤a ， 求得4≤a ＜8，故选A ．【点睛】本题主要考查函数的单调性，考查分段函数连续单调的问题.分段函数有两段，第一段是一次函数，第二段也是一次函数.对于一次函数，要单调递增就需要斜率大于零.两段分别递增还不行，还需要在两段交接的地方，左边比右边小，这样才能满足在R 身上单调递增. 11．D【分析】求出导函数'()2(1)f x a x =-，题意说明'()0f x ≤在[0,1]上恒成立（不恒等于0），从而得0a >，得开口方向，及函数单调性，再由函数性质可解.【详解】二次函数()22f x ax ax c ＝－＋在区间[]0,1上单调递减，则0a ≠，()()'210f x a x <＝－，所以0a >，即函数图象的开口向上，对称轴是直线1x ＝．所以f (0)＝f （2），则当()()0f m f ≤时，有02m ≤≤．【点睛】实际上对二次函数2()f x ax bx c =++，当0a >时，函数在(,]2b a -∞-递减，在[,)2b a -+∞上递增，当0a <时，函数在(,]2b a -∞-递增，在[,)2b a -+∞上递减. 12．A【分析】利用奇偶性与单调性把抽象不等式转化为具体不等式即可.【详解】∵奇函数()g x 是定义在R 上的减函数，且()()2f x g x =+,若()()24f m f m +-＞,，则g （m ）＞﹣g （m-2）=g （2﹣m ），∴m ＜2﹣m ，解得：m ＜1，故选A ．【点睛】根据抽象函数的单调性解不等式应注意以下三点：（1）一定注意抽象函数的定义域（这一点是同学们容易疏忽的地方，不能掉以轻心）；（2）注意应用函数的奇偶性（往往需要先证明是奇函数还是偶函数）；（3）化成()()()()f g x f h x ≥ 后再利用单调性和定义域列不等式组.13．12- 【分析】利用分段函数()y f x =的解析式，由内到外逐层计算()()2ff -的值.【详解】()2,166,1x x f x x x x ⎧≤⎪=⎨+->⎪⎩，()()2224f ∴-=-=， 因此，()()()61244642ff f -==+-=-. 故答案为：12-. 【点睛】本题考查分段函数值的计算，在计算多层函数值时，要遵循由内到外逐层计算，考查计算能力，属于基础题.14．2【分析】 先令112x a -=,可得()21x a =+,代回函数关系式可得()41f a a =-,进而求得a 【详解】 令112x a -=,()21x a ∴=+, ()()2215417f a a a ∴=⋅+-=-=,2a ∴=,故答案为：2【点睛】本题考查已知函数值求参数,考查函数转换的思想,属于基础题15．312【分析】根据集合相等的条件，分别讨论①正确、②正确、③正确，得出a 、b 、c 的值，从而可得出10010a b c ++的值.【详解】已知集合{}{},,1,2,3a b c =，且下列三个关系：①3a ≠；②3b =；③1c ≠，有且只有一个正确.若①正确，则3a ≠，3b ≠，1c =，不成立；若②正确，则3a =，1c =，3b =，不成立；若③正确，则3a =，3b ≠，1c =，2b ∴=.因此，10010312a b c ++=. 故答案为：312. 【点睛】本题考查集合相等条件的应用，以及分类讨论思想，注意列举时按一定的顺序列举，做到不重不漏，考查推理能力，属于基础题. 16．()(),21,-∞-⋃+∞ 【分析】分析出函数()y f x =在区间[)0,+∞上为增函数，由偶函数的性质得出()()2f t a f t +>-，可得出2t a t +>-，不等式两边平方后得出()22440a t a ++->，构造函数()()2244g t a t a =++-，得出()10220g g ⎧⎛⎫>⎪ ⎪⎝⎭⎨⎪>⎩，可得出关于实数a 的不等式组，解出即可. 【详解】当0x ≥时，()()14341111x x f x x x x +--===-+++， 所以，函数()y f x =在区间[)0,+∞上为增函数.()()20f t a f t +-->，()()2f t a f t ∴+>-，即()()2f t a f t +>-.所以，2t a t +>-，不等式两边平方得()22440a t a ++->.构造函数()()2244g t a t a =++-，由题意知，不等式()0g t >对任意的1,22t ⎡⎤∈⎢⎥⎣⎦恒成立，则()2212022440g a a g a a ⎧⎛⎫=+->⎪ ⎪⎝⎭⎨⎪=++>⎩，解得2a <-或1a >，因此，实数a 的取值范围是()(),21,-∞-⋃+∞. 故答案为：()(),21,-∞-⋃+∞. 【点睛】本题考查利用函数的单调性与偶函数的性质解函数不等式，同时也涉及了一次函数不等式在区间上恒成立，考查化归与转化思想的应用，属于中等题. 17．（1）B ∩A =[1，4），B ∩(∁U A )= [-4,1)∪[4,5)；（2）1[,)2+∞ . 【分析】(1)利用补集的定义求出A 的补集,然后根据交集的定义求解即可直接求解即可；(2 )分类讨论B 是否是空集，列出不等式组求解即可. 【详解】（1）∵A ={x |1≤x ＜4}，∴∁U A ={x |x ＜1或x ≥4}，∵B ={x |2a ≤x ＜3-a }，∴a =-2时，B ={-4≤x ＜5}，所以B ∩A =[1，4）， B ∩(∁U A )={x |-4≤x ＜1或4≤x ＜5}=[-4,1)∪[4,5). （2）A ∪B =A ⇔B ⊆A ， ①B =∅时，则有2a ≥3-a ，∴a ≥1, ②B ≠∅时，则有，∴,综上所述，所求a 的取值范围为.【点睛】本题主要考查集合的交集、集合的补集以及空集的应用，属于简答题.要解答本题，首先必须熟练应用数学的转化与划归思想及分类讨论思想，将并集问题转化为子集问题，其次分类讨论进行解答，解答集合子集过程中，一定要注意空集的讨论，这是同学们在解题过程中容易疏忽的地方，一定不等掉以轻心. 18．（1）32；（2）17x x -+=，1122x x --=【分析】（1）利用指数幂的运算律可计算出所求代数式的值；（2）将等式11223x x -+=两边平方可得出1x x -+的值，将代数式1122x x --平方即可计算出1122x x --的值.【详解】（1）原式()()()122143431310222104422---=-++-=-++-=；（2）在等式11223x x -+=两边平方得129x x -++=，则17x x -+=．2111222725x x x x --⎛⎫-=+-=-= ⎪⎝⎭，则1122x x --=【点睛】本题考查指数幂的计算，同时也考查了整体代换思想的应用，考查计算能力，属于基础题.19．()min2,11,1a a f x a a-<⎧⎪=⎨-≥⎪⎩【分析】讨论0a =和0a ≠的情况，然后再分对称轴和区间之间的关系，最后求出最小值 【详解】当0a =时，()2f x x =-，它在[]01，上是减函数 故函数的最小值为()12f =-当0a ≠时，函数()22f x ax x =-的图象思维对称轴方程为1x a=当1a ≥时，](101a ∈，，函数的最小值为11f a a ⎛⎫=- ⎪⎝⎭当01a <<时，11a>，函数的最小值为()12f a =- 当0a <时，11a<，函数的最小值为()12f a =- 综上，()2,11,1mina a f x a a-<⎧⎪=⎨-≥⎪⎩【点睛】本题主要考查了二次函数在闭区间上的最值，二次函数的性质的应用，体现了分类讨论的数学思想，属于中档题．20．（1）22101200(010){902000(1020)t t t y t t t -++≤≤=-+<≤（2）max 1225y =，min 600y =【分析】 （1），写成分段函数的形式，并且化简可得函数表达式；（2）根据（1）的结果，可得分段函数的每段都是二次函数，所以分别求两段函数的最值，再进行比较，最大的就是最大值，最小的就是最小值. 【详解】解：（1）由已知得：1(15)(802)(010)2()()1(25)(802)(1020)2t t t y f t g t t t t ⎧+-≤≤⎪⎪=⋅=⎨⎪--<≤⎪⎩=22101200(010)902000(1020)t t t t t t ⎧-++≤≤⎨-+<≤⎩ （2）由（1）知①当010t ≤≤时，22101200(5)1225=-++=--+y t t t .该函数在[0,5]递增，在（5,10]递减．max 12255y t ∴==（当时取得），min 1200010y t t ∴===（当或时取得）．②当1020t <≤时，22902000(45)25=-+=--y t t t .该函数在（10,20]递减，min 20008001200,60020y y t ∴<-===（当时取得）． 由①②知max 12255y t ∴==（当时取得），min 60020y t ==（当时取得）考点：1.函数的实际应用；2.分段函数的最值. 21．（1）()21xf x x =+；（2）(][),11,-∞⋃+∞. 【分析】（1）根据奇函数的性质求b ，再代值计算求出a ；（2）求出函数f （x ）的最大值即可，根据基本不等式即可求出． 【详解】 （1）()()f x f x -=-，()()0f x f x ∴-+=，22011ax b ax bx x -++∴+=++对一切x 成立， 即2201b x =+恒成立，0b ∴=，()21axf x x ∴=+． 又1225f ⎛⎫=⎪⎝⎭，1a ∴=. ()21x f x x ∴=+． （2）在区间[]2,4上任取1x ，2x ，且1224x x ≤≤≤，则()()()()()()221222121222221212111111x x x x x x f x f x x x x x +-+-=-=++++， ()()()()()()()()12211221122222121211111x x x x x x x x x x x x x x -+---==++++．1224x x ∴≤≤≤，210x x ∴->，1210x x ->， 又2110x +>，2210x +>，故知()()()()211222121011x x x x x x -->++，()()120f x f x ∴->，()()12f x f x >．故知，函数在[]2,4上单调递减．()()max 225f x f ∴==． 若()235f x m ≤-区间[]2,4恒成立，()2max 35f x m ≤-，即22355m ≤-，21m ∴>，21m ∴≤-或1m ≥，m ∴的取值范围是(][),11,-∞⋃+∞．【点睛】本题考查了函数恒成立的问题以及奇函数的性质和基本不等式，属于中档题．22．(1) [3,0]-； (2) 2617,(3),()8,(30),8,(0).a a g a a a a +≤-⎧⎪=--<<⎨⎪≥⎩；(3)(4,)-+∞.【解析】试题分析：（1）利用函数单调性得证明方法证明函数在[1,2]上是增函数，利用单调性求其值域；（2）通过换元法，问题转化为二次函数求最小值，利用对称轴分类讨论即可；（3）分离参数，求函数的最值，求最值时利用函数单调性.试题解析：(1) 在[1,2]任取12,x x 且12x x <，则210x x ->，120x x ⋅>， 所以，211221212112()(4)44()()()()0x x x x f x f x x x x x x x -⋅⋅+-=---=>⋅，即21()()f x f x >， 所以4()f x x x=-是[1,2]上增函数，故当1x =时，()f x 取得最小值3-，当2x =时，()f x 取得最大值0，所以函数()f x 的值域为[3,0]-. (2) 22216444()2()()2()8F x x a x x a x x x x x=+--=---+，[1,2]x ∈， 令4x t x-=，[3,0]t ∈-，则222()28()8h t t at t a a =-+=-+-. ①当3a ≤-时，()h t 在[3,0]-上单调递增，故()(3)617g a h a =-=+；②当0a ≥时，()h t 在[3,0]-上单调递减，故()(0)8g a h ==；③当30a -<<时，()h t 在[3,]a -上单调递减，在[,0]a 上单调递增，故2()()8g a h a a ==-；综上所述，2617,(3),()8,(30),8,(0).a a g a a a a +≤-⎧⎪=--<<⎨⎪≥⎩(3)由(2)知，当(3,0)a ∈-时，2()8g a a =-，所以2()24g a a at >-++， 即22824a a at ->-++，整理得，24at a <+. 因为0a <，所以4t a a>+对于任意的(3,0)a ∈-时恒成立. 令4()a a aϕ=+，(3,0)a ∈-，问题转化为max ()t a ϕ>. 在(3,0)-任取12,a a 且12a a <，则210a a ->，120a a ⋅>， 所以，211221212112()(4)44()()()()a a a a a a a a a a a a ϕϕ-⋅⋅--=+-+=⋅， ①当12,(3,2]a a ∈--时，124a a ⋅>，所以21()()0a a ϕϕ->，即21()()a a ϕϕ>， 所以函数4()a a aϕ=+在(3,2]--上单调递增； ②当12,[2,0)a a ∈-时，124a a ⋅<，所以21()()0a a ϕϕ-<，即21()()a a ϕϕ<， 所以函数4()a a aϕ=+在[2,0)-上单调递减； 综上，max ()(2)4a ϕϕ=-=-，从而4t >-. 所以，实数t 的取值范围是(4,)-+∞.试题点睛：本题涉及函数单调性定义，利用单调性求函数最值，分类讨论等内容，属于难题.解题时注意分析函数增减性及其应用，特别是含参数的函数求最值时，要注意分类讨论，过程要不重不漏.。

东海高级中学—20XX学年度第一学期高二第三次月考英语试题范围: Units 6-8 BII 考试时间: 120分钟，共150分命题人：刘恩县第一卷（三部分，共115分）第一部分：听力（共两节，满分30分）第一节：（共5小题：每小题1.5分,满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What time is it?A. 8:00.B. 9:00.C. 10:00.2. What is Peter going to do this afternoon?A. Play basketball.B. Ride a bicycle.C. Go swimming.3. How much is the woman going to pay?A. 20 pence.B. 25 pence.C. 30 pence.4. How will the man travel to New York?A. By car.B. By train.C. By plane.5. What is the woman doing?A. Making a suggestion.B. Asking for help.C. Offering advice.第二节：(共15小题：每题1.5分,满分22.5分)听下面5段对话或独白，每段对话后或独白后有几个小题。

从题中所给的A、B、C 三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话读两遍。

听第6段对话，回答6至7题。

6. What does the man do?A. He's an engineer.B. He's a salesman.C. He's a traveler.7. What's the relationship between the two speakers?A. They are friends.B. They are strangers.C. They are shop assistant and customer.听第7段对话，回答8至9题。

东海高级中学2004---2005学年度高一月考试卷物理（时间：90分钟满分：100分）一、选择题（本大题总分为40分。

每小题有一个或者多个选项符合题目要求，全对的得4分，不全的得2分，多选或选错的得0分。

）1.匀速圆周运动属于：( )A.匀速运动B.匀加速运动C.加速度不变的曲线运动D.变加速的曲线运动2.关于运动的性质，以下说法中正确的是：( )A.变速运动一定是曲线运动；B.曲线运动一定是变速运动；C.曲线运动一定是加速度变化的运动；D.运动物体的加速度数值、速度数值都不变的运动一定是直线运动．3.甲、乙两人从距地面h高处水平抛出两个小球,甲球的落地点距抛出点的水平距离是乙的2倍,不计空气阻力,为了使乙球的落地点与甲球相同,则乙球抛出点的高度可能为：( )A.2hB.2hC.4hD.3h4.飞机驾驶员最大可承受9倍的重力加速度带来的影响．若飞机在竖直平面上沿圆弧轨道俯冲时的速度为v，则圆弧的最小半径为( )A.v2/9gB.v2/8g C．v2/10g D．v2/g5.宇航员在绕地球运转的太空空间站中写字，他应选择下列哪一种笔( )A．钢笔B．圆珠笔C．铅笔D．毛笔6．在研究宇宙发展演变的理论中，有一种学说叫做“宇宙膨胀说”，这种学说认为万有引力常量G在缓慢地减小，根据这一理论，在很久很久以前，太阳系中地球的公转情况与现在相比( )A.公转半径R较大B.公转周期T较小C.公转速率v较大D.公转角速度ω较小7.如图所示，木板B托着木块A在竖直平面内做匀速圆周运动，从水平位置a到最高点b的过程中( )A.B对A的支持力越来越大B.B对A的支持力越来越小C.B对A的摩擦力越来越大D.B对A的摩擦力越来越小8.我国是世界上能够发射地球同步卫星的少数国家之一，关于同步卫星，正确的说法是( )A.可以定点在北京上空B．运动周期与地球自转周期相同的卫星肯定是同步卫星C.同步卫星内的仪器处于超重状态D．同步卫星轨道平面与赤道平面重合9．如图所示，一个物体以v0=10m/s的初速度水平抛出，不计空气阻力，g取10m/s2，3s后物体到达P点的速度与水平方向的夹角θ为（）A、30ºB、45ºC、60ºD、75º10．如图所示，物体A和B的质量均为m，且分别与跨过的定滑轮的轻绳连接，不计绳与滑轮、滑轮与轴间的摩擦，在水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中，则（）A.物体A也做匀速直线运动B.绳子拉力始终等于物体A所受重力C.绳子拉力始终大于物体A所受重力D.绳子对A物体的拉力一直保持不变二、填空题（每题4分，共20分）11.钟表上的时针、分针和秒针运行时的角速度之比为_____________；如果三针的长度之比为1∶2∶3，那么三针尖端的线速度之比为_____________。

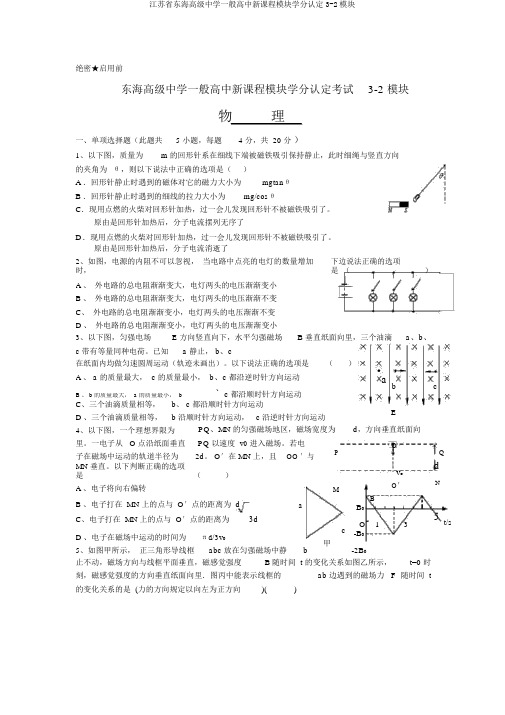
绝密★启用前东海高级中学一般高中新课程模块学分认定考试3-2 模块物理一、单项选择题（此题共 5 小题，每题 4 分，共 20 分）1、以下图，质量为m 的回形针系在细线下端被磁铁吸引保持静止，此时细绳与竖直方向的夹角为θ，则以下说法中正确的选项是（）A ．回形针静止时遇到的磁体对它的磁力大小为mgtanθB ．回形针静止时遇到的细线的拉力大小为mg/cosθC．现用点燃的火柴对回形针加热，过一会儿发现回形针不被磁铁吸引了。

原由是回形针加热后，分子电流摆列无序了D．现用点燃的火柴对回形针加热，过一会儿发现回形针不被磁铁吸引了。

原由是回形针加热后，分子电流消逝了2、如图，电源的内阻不可以忽视，当电路中点亮的电灯的数量增加时，下边说法正确的选项是（）A 、外电路的总电阻渐渐变大，电灯两头的电压渐渐变小B 、外电路的总电阻渐渐变大，电灯两头的电压渐渐不变C、外电路的总电阻渐渐变小，电灯两头的电压渐渐不变D 、外电路的总电阻渐渐变小，电灯两头的电压渐渐变小3、以下图，匀强电场 E 方向竖直向下，水平匀强磁场 B 垂直纸面向里，三个油滴a、b、c 带有等量同种电荷。

已知 a 静止， b、c在纸面内均做匀速圆周运动（轨迹未画出）。

以下说法正确的选项是（A 、 a 的质量最大， c 的质量最小， b、c 都沿逆时针方向运动、c 都沿顺时针方向运动B 、 b 的质量最大， a 的质量最小， bC、三个油滴质量相等，b、 c 都沿顺时针方向运动D 、三个油滴质量相等， b 沿顺时针方向运动， c 沿逆时针方向运动4、以下图，一个理想界限为PQ、MN 的匀强磁场地区，磁场宽度为里。

一电子从 O 点沿纸面垂直PQ 以速度 v0进入磁场。

若电P 子在磁场中运动的轨道半径为2d。

O′在 MN 上，且OO ′与MN 垂直。

以下判断正确的选项是（）A 、电子将向右偏转MB 、电子打在 MN 上的点与 O′点的距离为 d a）ab cEd，方向垂直纸面向OQ ××××××××v o××dO′NBB0C、电子打在 MN 上的点与 O′点的距离为3dO135t/scD 、电子在磁场中运动的时间为πd/3v0-B0甲-2B05、如图甲所示，正三角形导线框abc 放在匀强磁场中静b止不动，磁场方向与线框平面垂直，磁感觉强度 B 随时间 t 的变化关系如图乙所示，t=0 时刻，磁感觉强度的方向垂直纸面向里．图丙中能表示线框的ab 边遇到的磁场力 F随时间 t 的变化关系的是 (力的方向规定以向左为正方向)()2F 0FFFF 0F 0F 0F 0O 1 3 5 7 t/sO 1 3 5 7 t/sO 1 3 5 7 t/sO 1 3 5 7 t/s-F 0- F 0-F 0- F 0-2F 0 -2F 0-2F 0 -2F 0A B C D丙二、多项选择题：（此题共 4 小题，每题 5 分，共 20 分）6、对于磁感线，以下说法中正确的选项是（）A、磁感线上某一点的切线方向就是该点的磁场方向；B、磁感线必定从磁体的 N 极出发，到 S 极停止；D、磁感线密处磁场强，磁感线疏处磁场弱；7、高温超导限流器由超导零件和限流电阻并联构成，如图。

江苏省东海高中2016届高三语文上学期10月月考试题（讲评卷，含解析）不分版本东海高级中学高三学分认定考试语文试题友情提醒1.本卷总分值160分，考试时间150分钟，选修历史的总分值200分，延时30分钟。

2.答题前，请将学校、姓名、考试号等填写在答题纸的规定位置。

3.请考生务必将所有选择题答案依据题目序号填涂在机读卡上，否那么无效。

4.请用0.5毫米黑色签字笔按题号在答题纸指定区域答题，否那么一律无效。

一、语言文字运用〔15分〕1.以下各句划横线处，成语使用恰当的一组是(3分) 〔▲〕①自古以来，台湾与大陆一直同属一个中国，台湾是中国领土不可分割的一局部的法律地位不容▲，更不容挑战。

②可下半场的最后5分钟内，我们差点将全场的劳动成果▲，所以说我们要拿下一场比赛还是要在5分钟之后才能确保。

③艺术家抚弄艺术，不是在乎其“市场价值〞，而是用来搭建心灵之“庐〞。

明代戏剧家祁彪佳说其寓园为▲之所，可寄寓心灵。

A．置疑功亏一篑安贫乐道 B．质疑功亏一篑安身立命C．质疑毁于一旦安贫乐道 D．置疑毁于一旦安身立命1. 〔3分〕D 解析：置疑，疑心，多用于否认，一般和“不容，无可，毋庸〞等表否认的词语组合，适合①空。

质疑，提出疑问。

毁于一旦：于，在；一旦，一天。

在一天的工夫全被毁掉，多指长期劳动的成果一下子被毁掉。

适合②空。

前功尽弃：功，功绩；尽，完全；弃，丧失。

以前的功绩全部丧失。

也指以前的努力全部白费。

安身立命：生活有着落，精神有所寄托，符合③语境。

安贫乐道：安于贫穷的境遇，乐于奉行自己信仰的道德准那么。

2．以下语句中，没有语病的一项为哪一项：〔3分〕〔▲〕A．来自中俄两军以及我国地方科研院校的专家学者共百余人，紧紧围绕“世界反法西斯战争与中国战场〞这一主题进行研讨交流。

B．门罗的许多小说写的是平凡小镇上的普通人物，因而文笔细腻、精致，能够精确把握节奏和气氛，准确拿捏人物心理。

C．中国著名女科学家屠呦呦所从事的科学工作，显著降低了疟疾患者，为促进人类健康和减少病患痛苦作出了无法估量的奉献。

江苏省连云港市东海县高级中学2014-2015学年高三10月月考试卷一、填空题:本大题共14小题，每小题5分，共计70分．不需写出解答过程，请把答案写在答题纸的指定位置上．1. 已知集合{}41，=A ,{}a B ,1,0=，{}4,1,0=⋃B A ，则a = ▲ ． 2. 若9=z z （其中z 表示复数z 的共轭复数），则复数z 的模为 ▲ ． 3. 已知向量)2,1(=a ，)2,3(-=b ，则b b a ⋅+)(＝ ▲ ．4. 若命题“,R x ∈∃使得012≤++ax ax ”为假命题，则实数a 的取值范围为 ▲ ． 5. 已知βα,的终边在第一象限，则“βα>”是“βαsin sin >”的 ▲ 条件． 6. 函数y ＝x e x 的最小值是 ▲ ．7. 已知数列{}n a 是首项为1a ，公差为(02)d d π<<的等差数列，若数列{cos }n a 是等比数列，则其公比为 ▲ ．8. 设函数x x x f sin 1)(-=在0x x =处取极值，则)2cos 1)(1(020x x ++= ▲ ．9. 已知函数()R a xax y ∈+=2在1=x 处的切线与直线012=+-y x 平行，且此切线也是圆0)13(22=+-++y m mx y x 的切线，则m = ▲ ．10. 在ABC ∆中，角A,B,C 的对边分别为a ,b ,c ，已知sin sin sin sin cos21A B B C B ++=，若23C π=，则ab= ▲ ． 11. 已知函数1)12(31)(223+-+-++=a a x a x x x f 若函数)(x f 在(]31，上存在唯一的极值点．则实数a 的取值范围为 ▲ ．12. 设函数)102)(36sin(2)(<<-+=x x x f ππ的图像与x 轴交于点A ，过点A 的直线l 与函数)(x f 的图像交于另外两点C B ,.O 是坐标原点，则OA OC OB •+)(= ▲ ．13. 在三角形ABC 中，已知AB=3，A=0120,ABC ∆，则BC BA u u u r u u u r g 的值= ▲ ．14. 无穷数列{}n a 中，12,,,m a a a L 是首项为10，公差为2-的等差数列；122,,,m m m a a a ++L 是首项为12，公比为12的等比数列（其中*3,m m ∈N ≥），并且对于任意的*n ∈N ，都有2n m n a a +=成立.记数列{}n a 的前n 项和为n S ,则使得12852013m S +≥*3,)m m ∈(N ≥的m 的取值集合为 ▲ ．二、解答题：本大题共6小题，共90分．请在答题卡指定区域．．．．．．．内作答. 解答时应写出文字说明、证明过程或演算步骤． 15. （本题满分14分）在锐角ABC ∆中，已知内角A 、B 、C 所对的边分别为a 、b 、c ，向量()()3,sin 2C A m +=，⎪⎭⎫ ⎝⎛-=12cos 2,2cos 2B B ，且向量,共线.（1）求角B 的大小；（2）如果1b =，求ABC ∆的面积ABC S ∆的最大值.16.（本题满分14分）已知函数)()14(log )(4R ∈++=k kx x f x是偶函数. (1)求k 的值;(2)设44()log (2)3x g x a a =⋅-,若函数()f x 与()g x 的图象有且只有一个公共点,求实数a 的取值范围.17.（本题满分14分）已知各项均为整数的数列{}n a 满足31a =-,74a =,前6项依次成等差数列,从第5项起依次成等比数列.A BM (1)求数列{}n a 的通项公式；(2)求出所有的正整数m ,使得1212m m m m m m a a a a a a ++++++=.18.（本题满分16分）为丰富农村业余文化生活，决定在N B A ,,三个村子的中间地带建造文化中心。

2016-2017学年江苏省连云港市东海高中高一（上）期中数学试卷一、填空题：本大题共14小题，每小题5分，共计70分.不需写出解答过程，请把答案直接填写在题中横线上.1．（5分）设集合A={3，m}，B={3m，3}，且A=B，则实数m的值是．2．（5分）函数f（x）=a x﹣2+2（a＞0且a≠1）必过定点．3．（5分）lg+2lg2﹣（）﹣1=．4．（5分）已知a=0.4﹣0.5，b=0.50.5，c=log0.22，则a，b，c的从大到小顺序是．5．（5分）函数y=的定义域为．6．（5分）函数y=log0.2（x2﹣2x﹣3）的单调递减区间为．7．（5分）函数y=log（x2﹣6x+17）的值域为．8．（5分）已知f（x）=则不等式xf（x）+x≤2的解集是．9．（5分）用二分法求函数f（x）=3x﹣x﹣4的一个零点，其参考数据如下：据此数据，可得方程3x﹣x﹣4=0的一个近似解（精确到0.01）是．10．（5分）已知函数f（x）=ax3﹣bx+1，若f（﹣2）=3，则f（2）=．11．（5分）已知函数f（x）=2×9x﹣3x+a2﹣a﹣3，当0≤x≤1时，f（x）＞0恒成立，则实数a的取值范围为．12．（5分）已知定义在R上的函数f（x）=2|x﹣m|﹣1（m为实数）为偶函数，记a=f（log0.53），b=f（log25），c=f（2m），则a，b，c的大小关系为．13．（5分）设方程x2﹣mx+1=0两根为α，β，且0＜α＜1，1＜β＜2，则实数m 的取值范围是．14．（5分）设函数f（x）=x|x﹣a|，若对于任意x1，x2∈[3，+∞），x1≠x2，不等式＞0恒成立，则实数a的取值范围是．二、解答题（共6小题，满分90分）15．（14分）（Ⅰ）设log a2=m，log a3=n，求a2m+n的值；（Ⅱ）计算：log49﹣log212+10．16．（14分）设全集U=R，已知集合A={x||x﹣a|≤1}，B={x|（4﹣x）（x﹣1）≤0}．（1）若a=4，求A∪B；（2）若A∩B=A，求实数a的取值范围．17．（14分）已知函数f（x）=．（1）解不等式f（x）＜；（2）求函数f（x）值域．18．（16分）某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产产品x（百台），其总成本为G（x）（万元），其中固定成本为2.8万元，并且每生产1百台的生产成本为1万元（总成本=固定成本+生产成本）．销售收入R（x）（万元）满足，假定该产品产销平衡（即生产的产品都能卖掉），根据上述统计规律，请完成下列问题：（1）写出利润函数y=f（x）的解析式（利润=销售收入﹣总成本）；（2）要使工厂有盈利，求产量x的范围；（3）工厂生产多少台产品时，可使盈利最多？19．（16分）已知定义域为R的函数f（x）=是奇函数，（1）求a的值；（2）试判断f（x）在（﹣∞，+∞）的单调性，并请你用函数单调性的定义给予证明；（3）若对任意的t∈R，不等式f（mt2+1）+f（1﹣mt）＜0恒成立，求实数t的取值范围．20．（16分）设二次函数f（x）=ax2+bx+c（a≠0）在区间[﹣2，2]上的最大值、最小值分别是M、m，集合A={x|f（x）=x}．（1）若A={1，2}，且f（0）=2，求M和m的值；（2）若A={1}，且a≥1，记g（a）=M+m，求g（a）的最小值．2016-2017学年江苏省连云港市东海高中高一（上）期中数学试卷参考答案与试题解析一、填空题：本大题共14小题，每小题5分，共计70分.不需写出解答过程，请把答案直接填写在题中横线上.1．（5分）设集合A={3，m}，B={3m，3}，且A=B，则实数m的值是0．【解答】解：A=B；∴m=3m；∴m=0；故答案为：0．2．（5分）函数f（x）=a x﹣2+2（a＞0且a≠1）必过定点（2，3）．【解答】解：因为指数函数f（x）=a x经过的定点是（0，1），所以函数f（x）=a x ﹣2+2结果的定点是（2，3）．故答案为：（2，3）．3．（5分）lg+2lg2﹣（）﹣1=﹣1．【解答】解：lg+2lg2﹣（）﹣1=lg5﹣lg2+2lg2﹣2=lg5+lg2﹣2=1﹣2=﹣1．故答案为﹣1．4．（5分）已知a=0.4﹣0.5，b=0.50.5，c=log0.22，则a，b，c的从大到小顺序是a ＞b＞c．【解答】解：由函数y=0.4x单调递减的性质可得a=0.4﹣0.5＞0.40=1，即a＞1；由函数y=0.5x单调递减的性质可得b=0.50.5＜0.50=1，即0＜b＜1；由函数y=log0.2x单调递减的性质可得c=log0.22＜log0.21=0，即c＜0．故可得a＞b＞c，故答案为：a＞b＞c5．（5分）函数y=的定义域为[1，2）．【解答】解：因为：要使函数有意义：所以：⇒⇒1≤x＜2．故答案为：[1，2）．6．（5分）函数y=log0.2（x2﹣2x﹣3）的单调递减区间为（3，+∞）．【解答】解：令t=x2﹣2x﹣3，t＞0∴t在（3，+∞）上是增函数又∵y=log0.2t在（3，+∞）是减函数根据复合函数的单调性可知：函数y=log0.2（x2﹣2x﹣3）的单调递减区间为（3，+∞）故答案为：（3，+∞）7．（5分）函数y=log（x2﹣6x+17）的值域为（﹣∞，﹣3] ．【解答】解：t=x2﹣6x+17=（x﹣3）2+8≥8在[8，+∞）上是减函数，所以y≤=﹣3，即原函数的值域为（﹣∞，﹣3]故答案为：（﹣∞，﹣3]8．（5分）已知f（x）=则不等式xf（x）+x≤2的解集是{x|x≤1} ．【解答】解：x≥0时，f（x）=1，xf（x）+x≤2⇔x≤1，∴0≤x≤1；当x＜0时，f（x）=0，xf（x）+x≤2⇔x≤2，∴x＜0．综上x≤1．故答案为：{x|x≤1}9．（5分）用二分法求函数f（x）=3x﹣x﹣4的一个零点，其参考数据如下：据此数据，可得方程3x﹣x﹣4=0的一个近似解（精确到0.01）是 1.56．【解答】解：由表格作数轴如下，故f（1.5625）f（1.5563）＜0；故方程3x﹣x﹣4=0的一个近似解在（1.5563，1.5625）之间，故可取（1.5563+1.5625）=1.5594≈1.56作为近似解．故答案为：1.56．10．（5分）已知函数f（x）=ax3﹣bx+1，若f（﹣2）=3，则f（2）=﹣1．【解答】解：∵f（﹣2）=3，∴﹣8a+2b+1=3，即﹣8a+2b=2，则f（2）=8a﹣2b+1=﹣2+1=﹣1，故答案为：﹣111．（5分）已知函数f（x）=2×9x﹣3x+a2﹣a﹣3，当0≤x≤1时，f（x）＞0恒成立，则实数a的取值范围为a＞2或a＜﹣1．【解答】解：∵0≤x≤1时，f（x）＞0恒成立，令t=3x，设f（t）=2t2﹣t+a2﹣a﹣3，1≤t≤3时为对称轴x=，开口向上的抛物线的一段单调递增函数则t=1即自变量x=0，得到f（x）的最小值f（0）＞0，化简得；a2﹣a﹣2＞0，解得a＞2或a＜﹣1故答案为a＞2或a＜﹣112．（5分）已知定义在R上的函数f（x）=2|x﹣m|﹣1（m为实数）为偶函数，记a=f（log0.53），b=f（log25），c=f（2m），则a，b，c的大小关系为b＞a＞c．【解答】解：∵定义在R上的函数f（x）=2|x﹣m|﹣1（m为实数）为偶函数，∴m=0，f（x）=2|x|﹣1，∴x∈（﹣∞，0）时，f（x）是减函数，x∈（0，+∞）时，f（x）是增函数，∵﹣1＜log0.52＜log0.53＜log0.51=0，log 25＞log24=2，∴a=f（log0.53）=﹣1∈（0，1），b=f（log25）=﹣1=4，c=f（2m）=2|0|﹣1=0，∴a，b，c的大小关系为b＞a＞c．故答案为：b＞a＞c．13．（5分）设方程x2﹣mx+1=0两根为α，β，且0＜α＜1，1＜β＜2，则实数m的取值范围是．【解答】解：方程x2﹣mx+1=0对应的二次函数f（x）=x2﹣mx+1，方程x2﹣mx+1=0两根根为α，β，且0＜α＜1，1＜β＜2，∴解得．故答案为：14．（5分）设函数f（x）=x|x﹣a|，若对于任意x1，x2∈[3，+∞），x1≠x2，不等式＞0恒成立，则实数a的取值范围是（﹣∞，3] ．【解答】解：∵对于任意x1，x2∈[3，+∞），x1≠x2，不等式＞0恒成立，∴函数f（x）=x|x﹣a|在[3，+∞）上是增函数．再由函数f（x）=x|x﹣a|的增区间是（﹣∞，）、（a，+∞），可得a≤3，故实数a的取值范围是（﹣∞，3]，故答案为：（﹣∞，3]．二、解答题（共6小题，满分90分）15．（14分）（Ⅰ）设log a2=m，log a3=n，求a2m+n的值；（Ⅱ）计算：log49﹣log212+10．【解答】解：（Ⅰ）因为log a2=m，log a3=n，所以a m=2，a n=3，所以a2m+n=a2m a n=4×3=12（Ⅱ）===﹣2+=16．（14分）设全集U=R，已知集合A={x||x﹣a|≤1}，B={x|（4﹣x）（x﹣1）≤0}．（1）若a=4，求A∪B；（2）若A∩B=A，求实数a的取值范围．【解答】解：（1）当a=4，A={x||x﹣a|≤1}={x|﹣1+a≤x≤1+a}={x|3≤x≤5}，B={x|（4﹣x）（x﹣1）≤0}={x|x≥4或x≤1}，∴A∪B={x|x≥3或x≤1}（2）A={x||x﹣a|≤1}={x|﹣1+a≤x≤1+a}，B={x|（4﹣x）（x﹣1）≤0}={x|x≥4或x≤1}，若A∩B=A，则A⊆B，∴﹣1+a≥4或1+a≤1，∴a≥5或a≤0．17．（14分）已知函数f（x）=．（1）解不等式f（x）＜；（2）求函数f（x）值域．【解答】解：（1）将f（x）的解析式代入不等式得：＜，整理得：3•4x﹣3＜4x+1，即4x=22x＜2=21，∴2x＜1，解得：x＜，则不等式的解集为{x|x＜}；（2）法一：f（x）==1+，∵4x＞0，∴4x+1＞1，∴﹣2＜＜0，∴﹣1＜1+＜1，则f（x）的值域为（﹣1，1）；法二：∵y=f（x）=，∴4x=＞0，即＜0，可化为：或，解得：﹣1＜y＜1，则f（x）的值域为（﹣1，1）．18．（16分）某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产产品x（百台），其总成本为G（x）（万元），其中固定成本为2.8万元，并且每生产1百台的生产成本为1万元（总成本=固定成本+生产成本）．销售收入R（x）（万元）满足，假定该产品产销平衡（即生产的产品都能卖掉），根据上述统计规律，请完成下列问题：（1）写出利润函数y=f（x）的解析式（利润=销售收入﹣总成本）；（2）要使工厂有盈利，求产量x的范围；（3）工厂生产多少台产品时，可使盈利最多？【解答】解：（1）由题意得G（x）=2.8+x．…（2分）∵，…（4分）∴f（x）=R（x）﹣G（x）=．…（6分）（2）∵f（x）=，∴当0≤x≤5时，由f（x）=﹣0.4x2+3.2x﹣2.8＞0，得1＜x≤5；．…（7分）当x＞5时，由f（x）=8.2﹣x＞0，得5＜x＜8.2．∴要使工厂有盈利，求产量x的范围是（1，8.2）．．…（8分）（3）∵f（x）=，∴当x＞5时，函数f（x）递减，∴f（x）＜f（5）=3.2（万元）．…（10分）当0≤x≤5时，函数f（x）=﹣0.4（x﹣4）2+3.6，当x=4时，f（x）有最大值为3.6（万元）．…（14分）所以当工厂生产4百台时，可使赢利最大为3.6万元．…（15分）19．（16分）已知定义域为R的函数f（x）=是奇函数，（1）求a的值；（2）试判断f（x）在（﹣∞，+∞）的单调性，并请你用函数单调性的定义给予证明；（3）若对任意的t∈R，不等式f（mt2+1）+f（1﹣mt）＜0恒成立，求实数t的取值范围．【解答】解：（1）∵定义域为R的函数f（x）=是奇函数，∴f（﹣x）===﹣f（x）=，∴a×2x+2=a+2x+1，解得a=2．检验：a=2时，f（x）=，∴f（﹣x）==，∴f（x）+f（﹣x）=0对x∈R恒成立，即f（x）是奇函数．∴当函数f（x）=是奇函数时，a的值为2．（2）由（1）知，f（x）在（﹣∞，+∞）上是单调递减函数．证明如下：令2x=t，则y===﹣（1﹣）=﹣，在（﹣∞，+∞）上任取x1，x2，令x1＜x2，∵t=2x在（﹣∞，+∞）上是增函数，∴0＜t1＜t2，∴y1﹣y2=（﹣）﹣（﹣）==，∵0＜t1＜t2，∴t2﹣t1＞0，t1+1＞0，t2+1＞0，∴y1﹣y2＞0，∴f（x）在（﹣∞，+∞）上是单调递减函数．（3）∵f（x）是奇函数，∴不等式f（mt2+1）+f（1﹣mt）＜0恒成立，等价于不等式f（mt2+1）＜f（mt ﹣1）恒成立，∵f（x）在R上是减函数，∴对任意的t∈R，mt2+1＞mt﹣1恒成立，整理，得：mt2﹣mt+2＞0对任意的t∈R恒成立，当m=0时，不等式为2＞0恒成立，符合题意；当m≠0时，，解得0＜m＜8．综上，实数m的取值范围为[0，8）．20．（16分）设二次函数f（x）=ax2+bx+c（a≠0）在区间[﹣2，2]上的最大值、最小值分别是M、m，集合A={x|f（x）=x}．（1）若A={1，2}，且f（0）=2，求M和m的值；（2）若A={1}，且a≥1，记g（a）=M+m，求g（a）的最小值．【解答】解：（1）由f（0）=2可知c=2，又A={1，2}，故1，2是方程ax2+（b﹣1）x+c=0的两实根．∴，解得a=1，b=﹣2∴f（x）=x2﹣2x+2=（x﹣1）2+1，因为x∈[﹣2，2]，根据函数图象可知，当x=1时，f（x）min=f（1）=1，即m=1；当x=﹣2时，f（x）max=f（﹣2）=10，即M=10．（2）由题意知，方程ax2+（b﹣1）x+c=0有两相等实根x1=x2=1，根据韦达定理得到：，即，∴f（x）=ax2+bx+c=ax2+（1﹣2a）x+a，x∈[﹣2，2]其对称轴方程为x==1﹣又a≥1，故1﹣∴M=f（﹣2）=9a﹣2m=则g（a）=M+m=9a﹣﹣1又g（a）在区间[1，+∞）上为单调递增的，∴当a=1时，g（a）min=赠送初中数学几何模型【模型一】“一线三等角”模型： 图形特征：60°60°60°45°45°45°运用举例：1.如图，若点B 在x 轴正半轴上，点A (4，4)、C (1，－1)，且AB ＝BC ，AB ⊥BC ，求点B 的坐标；2.如图，在直线l 上依次摆放着七个正方形（如图所示），已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是1S 、2S 、3S 、4S ，则14S S += ．ls 4s 3s 2s 13213. 如图，Rt △ABC 中，∠BAC =90°，AB =AC =2，点D 在BC 上运动（不与点B ，C 重合），过D 作∠ADE =45°，DE 交AC 于E ． （1）求证：△ABD ∽△DCE ；（2）设BD =x ，AE =y ，求y 关于x 的函数关系式，并写出自变量x 的取值范围； （3）当△ADE 是等腰三角形时，求AE 的长．EB4.如图，已知直线112y x =+与y 轴交于点A ，与x 轴交于点D ，抛物线212y x bx c =++与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为 (1，0)。

（考试时间120分钟，满分160分）一、填空题:本大题共14小题，每小题5分，共70分.请把正确答案填写在答题卡相应的位置上．1.集合{|21},{(,)|31}A x y x B x y y x ==-==+，则AB = ▲ .2.已知一个圆台的上、下底面半径分别为1,2cm cm ，高为3cm ，则该圆台的母线长为 ▲ .3.设函数()f x 是定义在R 上的奇函数，且()()f a f b >, 则()f a - ▲ ()f b -(填“>”或 “<”)4.如果,a b 是异面直线，直线c 与,a b 都相交，那么由这三条直线中的任意两条所确定的平面共为 ▲ 个.5.设{2,},{2,2}M m N m ==，且M N =，则实数m = ▲ .6. 在空间中，用a ，b ，c 表示三条不同的直线，γ表示平面，给出下列四个判断： （1）若//,//a b b c ，则//a c （2）若,a b b c ⊥⊥，则a c ⊥ （3）若//a γ，//b γ，则//a b （4）若a γ⊥，b γ⊥，则//a b 则所有正确的序号是 ▲ ．7.已知函数2,0,(),0,x x f x x x ≥⎧=⎨<⎩，则((2))f f -= ▲ .8. 设a b 、是两条不同的直线，α、β是两个不同的平面，给出下列四个判断： ①若,a b a α⊥⊥，则//b α ②若,a βαβ⊥⊥，则//a α ③若βα⊥a a ,//，βα⊥则 ④若,,ab a b αβ⊥⊥⊥，则αβ⊥其中正确的个数为 ▲ ．9. 已知正四棱锥的底面边长是6，则这个正四棱锥的侧面积是 ▲ ． 10. 长方体1111ABCD A B C D -中，13,2AB BC AA ===，则四面体11A BC D 的体积为 ▲ .11. 设βα,为两个不重合的平面，n m ,是两条不重合的直线，给出下列四个判断： ①若α⊥⊥m n m ,，则α//n ； ②若,,βα⊂⊂m n βα与相交且不垂直，则m n 与不垂直；③若βαα//,,//⊥n n m ，则β⊥m ； ④若n m m ⊥=⊥,,βαβα ，则n β⊥． 其中所有错误的序号是 ▲ .12.已知定义在实数集R 上的偶函数()f x 在区间[0,)+∞上是单调增函数，若3(1)(log )f f x <，则实数x 的取值范围为 ▲ .13. 现有如下判断或结论：①过平面外一点有且只有一条直线与该平面垂直；②过平面外一点有且只有一条直线与该平面平行；③如果两个平行平面和第三个平面相交，那么所得的两条交线平行；④如果两个平面相互垂直，那么经过第一个平面内一点且垂直于第二个平面的直线必在第一个平面内．则错误的个数是 ▲ ．14. 如图，在长方形ABCD 中，2,1,AB BC E ==为DC 的中点，F 为线段EC （端点除外）上一动点，现将AFD ∆沿AF 折起，使平面ABD ⊥平面ABC .在平面ABD 内过点D 作,DK AB K ⊥为垂足，设AK t =，则t 的取值范围是 ▲ ．二、解答题：本大题共6小题，共计90分.请在答．题纸指定区域内．．．．．．．作答，解答时应写出文字说明、证明过程或演算步骤.15.（本题满分14分）记函数()31f x x x =+---的定义域为集合M ，函数2()43g x x x =-+的值域为集合N ，求：（1）M ，N ； （2）,M N M N .16．（本题满分14分）如图,四边形ABCD 为平行四边形，四边形ADEF 是正方形，且BD ⊥平面CDE ，H 是BE 的中点,G 是AE ,DF 的交点. （1）求证:GH ∥平面CDE ； （2）求证:面ADEF ⊥面ABCD .17. （本题满分14分） 如图，在四棱锥A —BCDE 中，底面BCDE 是直角梯形， 90=∠BED ，BE ∥CD ，AB =6，BC =5，31=BE CD ，侧面ABE ⊥底面BCDE ，︒=∠90BAE ． ⇒ABBCDDE FFKDA 1A⑴求证：平面ADE ⊥平面ABE ；⑵过点D 作面α∥平面ABC ，分别于BE ，AE 交于点F ，G ，求DFG ∆的面积．18. （本题满分16分） 经市场调查，某超市的一种小商品在过去的近20天内的日销售量（件）与价格（元）均为时间t （天）的函数，且销售量近似满足g (t )＝80－2t （件），价格近似满足1()20|10|2f t t =--（元）．（1）试写出该种商品的日销售额y 与时间t （0≤t ≤20）的函数表达式； （2）求该种商品的日销售额y 的最大值与最小值．19. （本题满分16分）如图,在三棱柱111-ABC A B C 中，侧棱1AA ⊥底面ABC ,,⊥AB BC D 为AC 的中点,12A A AB ==,3BC =. （1）求证：1//AB 平面1BC D ；E BCD A线·············(2) 求四棱锥11-B AA C D 的体积.20. （本题满分16分） 已知a R ∈，函数()||f x x x a =-. （1）当2a =时，写出函数()y f x =的单调递增区间； （2）当2a >时，求函数()y f x =在区间[1,2]上的最小值；（3）设0a ≠，函数()y f x =在(,)m n 上既有最大值又有最小值，请分别求出,m n 的取值范围（用a 表示）。

2017-2018学年江苏省连云港市东海高级中学行知部高一（上）10月月考数学试卷一、填空题：本大题共14小题，每小题5分，共70分．1．已知集合A={x|x2﹣2x=0}，B={0，1，2}，则A∩B=．2．若集合A={x|kx2+4x+4=0}，x∈R中只有一个元素，则实数k的值为．3．某班共有40人，其中18人喜爱篮球运动，20人喜爱乒乓球运动，12人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为．4．函数y=3x+的值域是．5．函数f（x）=+2的单调递减区间是．6．求函数f（x）=x2﹣2x+3，x∈[﹣1，2]的值域．7．已知函数f（x）=2x2﹣4kx﹣5在区间[﹣1，2]上不具有单调性，则k的取值范围是．8．若函数f （x）=是R上的奇函数，则a=．9．已知函数f（x）的定义域为（﹣1，0），则函数f（2x+1）的定义域为．10．计算：=．11．若f（x），g（x）都是奇函数，且F（x）=af（x）+bg（x）+2在区间（0，+∞）上有最大值8，则在区间（﹣∞，0）上的最小值是．12．设函数y=f（x）是定义在[﹣2，2]上的偶函数，当x≥0时，f（x）单调递减，若f（1﹣a）＜f（a）成立，则实数a的取值范围是．13．设f （x）是R上的奇函数，且f（x+2）=﹣f（x），当0≤x≤1时，f（x）=x，则f=．14．已知函数f（x）=满足对任意的x1≠x2，都有＜0成立，则a的取值范围是．二、解答题：本大题共6小题，共90分．解答时应写出必要的文字说明、证明过程或演算步骤．15．已知集合A={x|0＜x﹣a≤5}，B=．（1）若A⊆B，求a的取值范围；（2）若B⊆A，求a的取值范围；（3）集合A与B能够相等？若能，求出a的值，若不能，请说明理由．16．根据下列条件，求函数f （x）的解析式：（1）已知一次函数f （x）满足f（f（x））=4x﹣1；（2）已知f（x+1）=x2+x+1．17．已知函数f（x）对任意实数x，y恒有f（x+y）=f（x）+f（y），且当x＞0时，f（x）＜0．（1）判断函数f（x）的奇偶性，并给出证明；（2）求证：函数f（x）是R上的减函数．18．如图所示，某动物园要建造两个一面靠墙的矩形熊猫活动室．如果可供建造围墙的材料总长是30m，那么，如何建造才能使熊猫活动室的面积最大？最大面积是多少？（假设围墙足够长）19．已知函数，其中a＞0，且a≠1．（1）若0＜a＜1，求不等式f（x）＜1的解集；（2）求关于不等式f（x）≥g（x）的解集．20．设函数f（x）=a x+（k﹣1）a﹣x+k2（a＞0，a≠1）是定义在R上的奇函数．（1）求k的值；（2）若f（1）＞0，求使不等式f（x2+x）+f（t﹣2x）＞0恒成立的t的取值范围；（3）若，设g（x）=a2x+a﹣2x﹣2mf（x），g（x）在[1，+∞）上的最小值为﹣1，求m的值．2017-2018学年江苏省连云港市东海高级中学行知部高一（上）10月月考数学试卷参考答案与试题解析一、填空题：本大题共14小题，每小题5分，共70分．1．已知集合A={x|x2﹣2x=0}，B={0，1，2}，则A∩B={0，2} ．【考点】1E：交集及其运算．【分析】求出A中方程的解确定出A，找出A与B的交集即可．【解答】解：由A中方程变形得：x（x﹣2）=0，解得：x=0或x=2，即A={0，2}，∵B={0，1，2}，∴A∩B={0，2}；故答案为：{0，2}2．若集合A={x|kx2+4x+4=0}，x∈R中只有一个元素，则实数k的值为0或1．【考点】1C：集合关系中的参数取值问题．【分析】集合A表示的是方程的解；讨论当二次项系数为0时是一次方程满足题意；再讨论二次项系数非0时，令判别式等于0即可．【解答】解：当k=0时，A={x|4x+4=0}={﹣1}满足题意当k≠0时，要集合A仅含一个元素需满足△=16﹣16k=0解得k=1故k的值为0；1故答案为：0或13．某班共有40人，其中18人喜爱篮球运动，20人喜爱乒乓球运动，12人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为8．【考点】1I：子集与交集、并集运算的转换．【分析】因为共40人，有12人对着两项运动都不喜爱，则热爱这两项运动的有40﹣12=28（人），因为18人喜爱篮球运动，20人喜爱兵乓球运动，则两项都喜欢的有18+20﹣28=10（人）．【解答】解：18﹣（[18+20﹣（40﹣12）]=8（人）；答：既喜爱篮球运动又喜爱乒乓球运动的人数为8人；故答案为：84．函数y=3x+的值域是[3，+∞）．【考点】34：函数的值域．【分析】利用换元法换化为二次函数问题即可求解值域．【解答】解：函数y=3x+，设=t，则t≥0，那么x=t2+1．可得函数y=3（t2+1）+t=3t2+t+3，t≥0．其对称轴t=，开口向上，∴函数y在[0，+∞）上单调递增，∴当t=0时，y取得最小值为3．∴函数y=3x+的值域是[3，+∞）．故答案为[3，+∞）．5．函数f（x）=+2的单调递减区间是（﹣∞，0）和（0，+∞）．【考点】3E：函数单调性的判断与证明．【分析】函数f（x）=+2的图象是由y=的图象向上平移两个单位得到的，故单调区间与反比例函数y=的一致，进而得到答案．【解答】解：函数f（x）=+2的图象是由y=的图象向上平移两个单位得到的，故单调区间与反比例函数y=的一致，即函数f（x）=+2的单调递减区间是（﹣∞，0）和（0，+∞），故答案为：（﹣∞，0）和（0，+∞）6．求函数f（x）=x2﹣2x+3，x∈[﹣1，2]的值域[2，6] ．【考点】3X：二次函数在闭区间上的最值．【分析】首先把二次函数的一般式转化成顶点式，进一步求出对称轴方程利用定义域和对称轴方程的关系求的结果．【解答】解：函数f（x）=x2﹣2x+3=（x﹣1）2+2所以：函数为开口方向向上，对称轴为x=1的抛物线由于x∈[﹣1，2]当x=1时，f（x）min=f（1）=2当x=﹣1时，f（x）max=f（﹣1）=6函数的值域为：[2，6]故答案为：[2，6]7．已知函数f（x）=2x2﹣4kx﹣5在区间[﹣1，2]上不具有单调性，则k的取值范围是（﹣1，2）．【考点】3W：二次函数的性质．【分析】若函数f（x）=2x2﹣4kx﹣5在区间[﹣1，2]上不具有单调性，则对称轴在区间（﹣1，2）上，进而得到答案．【解答】解：∵函数f（x）=2x2﹣4kx﹣5的图象的对称轴为x=k，若函数f（x）=2x2﹣4kx﹣5在区间[﹣1，2]上不具有单调性，则k∈（﹣1，2），故答案为：（﹣1，2）．8．若函数f （x）=是R上的奇函数，则a=﹣1．【考点】3L：函数奇偶性的性质．【分析】根据奇函数的性质推断出f（0）=0求得a的值【解答】解：∵函数f（x）在R上时奇函数，∴f（0）==0，∴a=﹣1，故答案为：﹣1．9．已知函数f（x）的定义域为（﹣1，0），则函数f（2x+1）的定义域为（﹣1，﹣）．【考点】33：函数的定义域及其求法．【分析】由给出的函数f（x）的定义域为（﹣1，0），直接由﹣1＜2x+1＜0求得x的范围得答案．【解答】解：∵函数f（x）的定义域为（﹣1，0），∴由﹣1＜2x+1＜0，解得：﹣1．∴函数f（2x+1）的定义域为（﹣1，﹣）．故答案为：（﹣1，﹣）．10．计算：=．【考点】46：有理数指数幂的化简求值．【分析】根据指数幂的运算性质计算即可．【解答】解：原式=（0.4）﹣1+（﹣2）+24×（﹣0.75）+0.5=﹣1+++=，故答案为：11．若f（x），g（x）都是奇函数，且F（x）=af（x）+bg（x）+2在区间（0，+∞）上有最大值8，则在区间（﹣∞，0）上的最小值是﹣4．【考点】3L：函数奇偶性的性质．【分析】利用f（x）、g（x）的奇偶性可判断F（x）﹣2的奇偶性，由F（x）在（0，+∞）上的最大值可得F（x）﹣2的最大值，由其奇偶性可得F（x）﹣2在对称区间（﹣∞，0）上的最值情况，从而可得F（x）的最值情况【解答】解：由F（x）=af（x）+bg（x）+2，得F（x）﹣2=af（x）+bg（x），∵f（x）和g（x）都是奇函数，∴F（﹣x）﹣2=af（﹣x）+bg（﹣x）=﹣af（x）﹣bg（x）=﹣[af（x）+bg（x）]=﹣[F（x）﹣2]，∴F（x）﹣2是奇函数，∵F（x）在（0，+∞）上有最大值8，即F（x）≤8，∴F（x）﹣2≤6，当x∈（﹣∞，0）时，﹣x∈（0，+∞），则F（﹣x）﹣2≤6，即﹣[F（x）﹣2]≤6，∴F（x）﹣2≥﹣6，即F（x）≥﹣4，∴x∈（﹣∞，0）时，F（x）有最小值﹣4，故答案为：﹣4．12．设函数y=f（x）是定义在[﹣2，2]上的偶函数，当x≥0时，f（x）单调递减，若f（1﹣a）＜f（a）成立，则实数a的取值范围是．【考点】3N：奇偶性与单调性的综合．【分析】根据f（x）为定义在[﹣2，2]上的偶函数，以及x≥0时f（x）单调递减便可由f（1﹣a）＜f（a）得到，从而解该不等式组便可得出a的取值范围．【解答】解：∵f（x）为定义在[﹣2，2]上的偶函数，∴由f（1﹣a）＜f（a）得，f（|1﹣a|）＜f（|a|），又x≥0时，f（x）单调递减，∴，解得﹣1≤a＜．∴a的取值范围为．故答案为．13．设f （x）是R上的奇函数，且f（x+2）=﹣f（x），当0≤x≤1时，f（x）=x，则f=0.5．【考点】3L：函数奇偶性的性质．【分析】根据题意，分析可得f（x+4）=﹣f（x+2）=f（x），即函数f （x）的周期为4，则有f=f（1.5+4×504）=f（1.5），进而分析可得f（1.5）=﹣f（﹣0.5）=f（0.5），结合函数的解析式可得答案．【解答】解：根据题意，f （x）满足f（x+2）=﹣f（x），则有f（x+4）=﹣f（x+2）=f（x），即函数f （x）的周期为4，f=f（1.5+4×504）=f（1.5），又由f（x+2）=﹣f（x），则f（1.5）=f（﹣0.5+2）=﹣f（﹣0.5），又由函数为奇函数，则f（﹣0.5）=﹣f（0.5）；又由当0≤x≤1时，f（x）=x，则f（0.5）=0.5；故答案为：0.5．14．已知函数f（x）=满足对任意的x1≠x2，都有＜0成立，则a的取值范围是（0，] ．【考点】5B：分段函数的应用；3F：函数单调性的性质．【分析】由已知可得：函数f（x）=在R上为减函数，进而，解得a的取值范围．【解答】解：对任意的x1≠x2，都有＜0成立，则函数f（x）=在R上为减函数，∴，解得a∈（0，]，故答案为：（0，]二、解答题：本大题共6小题，共90分．解答时应写出必要的文字说明、证明过程或演算步骤．15．已知集合A={x|0＜x﹣a≤5}，B=．（1）若A⊆B，求a的取值范围；（2）若B⊆A，求a的取值范围；（3）集合A与B能够相等？若能，求出a的值，若不能，请说明理由．【考点】18：集合的包含关系判断及应用．【分析】先解出集合A，再根据集合间的关系求解a的取值范围即可．【解答】解：（1）∵集合A={x|0＜x﹣a≤5}={x|a＜x＜a+5}，B=．A⊆B，∴，解得0≤a≤1，∴a的取值范围是[0，1]．（2）∵B⊆A，∴，解得a∈∅．（3）A=B时，，无解．∴集合A与B不能相等．16．根据下列条件，求函数f （x）的解析式：（1）已知一次函数f （x）满足f（f（x））=4x﹣1；（2）已知f（x+1）=x2+x+1．【考点】36：函数解析式的求解及常用方法．【分析】（1）利用待定系数法，可得f（x）的解析式．（2）利用凑配法，可得f（x）的解析式．【解答】解：（1）∵已知f（x）是一次函数，设f（x）=kx+b （k≠0），则f（f（x））=k（kx+b）+b，∴由f（f（x））=4x﹣1 可得k（kx+b）+b=4x﹣1，即k2x+kb+b=4x﹣1，∴k2=4，且kb+b=﹣1．解得k=﹣2，b=1，或者k=2，b=﹣，故f（x）的解析式为f（x）=﹣2x+1，或f（x）=2x﹣；（2）∵f（x+1）=x2+x﹣1=（x+1）2﹣（x+1）+1．∴f（x）=x2﹣x+1．17．已知函数f（x）对任意实数x，y恒有f（x+y）=f（x）+f（y），且当x＞0时，f（x）＜0．（1）判断函数f（x）的奇偶性，并给出证明；（2）求证：函数f（x）是R上的减函数．【考点】3P：抽象函数及其应用．【分析】（1）取x=y=0可求得f（0），取y=﹣x可得f（x）与f（﹣x）的关系，由奇偶性的定义即可判断；（2）任取x1，x2∈（﹣∞，+∞）且x1＜x2，由已知可得f（x2）+f（﹣x1）=f（x2﹣x1）＜0，从而可比较f（x1）与f（x2）的大小关系，得到f（x1）＞f（x2）；【解答】（1）解：取x=y=0，则f（0+0）=2f（0），∴f（0）=0，取y=﹣x，则f（x﹣x）=f（x）+f（﹣x），∴f（﹣x）=﹣f（x）对任意x∈R恒成立，∴f（x）为奇函数．（2）证明：任取x1，x2∈（﹣∞，+∞）且x1＜x2，则x2﹣x1＞0，f（x2）+f（﹣x1）=f（x2﹣x1）＜0，∴f（x2）＜﹣f（﹣x1），又f（x）为奇函数，∴f（x1）＞f（x2）．故f（x）为R上的减函数；18．如图所示，某动物园要建造两个一面靠墙的矩形熊猫活动室．如果可供建造围墙的材料总长是30m，那么，如何建造才能使熊猫活动室的面积最大？最大面积是多少？（假设围墙足够长）【考点】7F：基本不等式．【分析】设矩形的长宽分别为x，y．（x，y＞0）．可得2x+3y=30．矩形面积S=2xy=≤，即可得出．【解答】解：设矩形的长宽分别为x，y．（x，y＞0）．可得2x+3y=30．矩形面积S=2xy=≤==75，当且仅当2x=3y=15时取等号．∴建造时取矩形的长宽分别为7.5，5m时，才能使熊猫活动室的面积最大，最大面积是75m2．19．已知函数，其中a＞0，且a≠1．（1）若0＜a＜1，求不等式f（x）＜1的解集；（2）求关于不等式f（x）≥g（x）的解集．【考点】7E：其他不等式的解法．【分析】（1）根据0＜a＜1，指数函数单调递减，即可求解不等式f（x）＜1的解集；（2）根据指数函数的性质，对底数a进行讨论即可求解．【解答】解：函数，其中a＞0，且a≠1．（1）当0＜a＜1时，f（x）=a3x+1是单调递减函数，∵f（x）＜1，即a3x+1＜a0，可得：3x+1＞0解得：x∴不等式的解集为{x|x}；（2）不等式f（x）≥g（x），即a3x+1≥a2x﹣5，当0＜a＜1时，可得：3x+1≤2x﹣5，解得：x≤﹣6；不等式的解集为{x|x≤﹣6}．当a＞1时，可得：3x+1≥2x﹣5，解得：x≥﹣6；不等式的解集为{x|x≥﹣6}．20．设函数f（x）=a x+（k﹣1）a﹣x+k2（a＞0，a≠1）是定义在R上的奇函数．（1）求k的值；（2）若f（1）＞0，求使不等式f（x2+x）+f（t﹣2x）＞0恒成立的t的取值范围；（3）若，设g（x）=a2x+a﹣2x﹣2mf（x），g（x）在[1，+∞）上的最小值为﹣1，求m的值．【考点】3R：函数恒成立问题；3L：函数奇偶性的性质．【分析】（1）由奇函数的定义，可得f（﹣x）+f（x）=0恒成立，化简整理，即可得到所求值；（2）结合函数的单调性和函数的奇偶性脱去f符号求解二次不等式即可；（2）由f（1）=，可得a=2，再令t=f（x）=2x﹣2﹣x，g（x）=t2﹣2mt+2=（t﹣m）2+2﹣m2，t≥f（1）=，讨论对称轴t=m，求解最小值为﹣1，解方程即可得到m的值．【解答】解：（1）∵函数f（x）=是定义域为R的奇函数，∴f（﹣x）+f（x）=a﹣x+（k﹣1）a x+k2+a x+（k﹣1）a﹣x+k2=k（a x+a﹣x）+2k2=0对于任意实数都成立．∴k=0；此时f（x）=a x﹣a﹣x，满足f（﹣x）=﹣f（x），即函数f（x）是奇函数．（2）由（1）知函数的解析式为f（x）=a x﹣a﹣x，∵f（1）＞0，即a＞0，a＞0，a≠1，可得：a＞1．结合指数函数的性质可得，f（x）是定义域内的增函数，那么：不等式f（x2+x）+f（t﹣2x）＞0恒成立，可得f（x2+x）＞﹣f（t﹣2x）∴f（x）是奇函数，也是增函数，等价于：x2+x＞2x﹣t即x2﹣x＞﹣t∵x2﹣x=（x）2﹣当x=时，x2﹣x取得最小值为，∴﹣t，即t故得t的取值范围时（，+∞）．（3）由，即a=0，a＞0，a≠1，可得：a=2．，（负值舍去），即有t=f（x）=2x﹣2﹣x定义域内的增函数，由x≥1，可得：t．∵g（x）=a2x+a﹣2x﹣2mf（x）=22x+2﹣2x﹣2m（2x﹣2﹣x）=（2x﹣2﹣x）2﹣2m（2x ﹣2﹣x）+2，即有函数h（t）=t2﹣2mt+2，t∈[，+∞）其对称轴t=m．当m时，h（t）min=h（）=﹣1，即（）2﹣2m×+2=﹣1，可得：m=＞（舍去）当m时，h（t）min=h（m）=﹣1，即（m）2﹣2m×m+2=﹣1，可得：m=3，故满足题意的m的值为3．。

江苏省东海高级中学高三学分认定考试语文试题答案一、语言文字运用（15分）1．【答案】A（B，协奏曲；C，震撼力唾．（tuò）手可得；D，笑眯眯箪食．（shí）壶浆）2.【答案】C“作茧自缚”是指自己做的事不利于自己，反使自己陷入不利的境地；而“玩火自焚”是指干冒险或害人的事，最后害了自己，关键就是所干的事情的性质，前者只是不利己的事,后者则是既损人又不利己的事。

“间不容发”指空隙中容不下一根头发。

比喻与灾祸相距极近或情势危急到极点；“刻不容缓”指形势紧迫，一刻也不允许拖延。

前者指危险或危情迫在眉睫，但尚未发生；后者指对于已经发生的危险或危情必须立即处理解决，不容耽搁了。

“骇人听闻”是事情使人听了非常吃惊、害怕；“危言耸听”是指故意说些夸大的吓人的话，使人吃惊。

3．【答案】（1）必须是正在进行的不法侵害行为（2）只针对不法侵害的实施（3）不能超过必要的限度（4）必须针对不法侵害者本人实施。

（评分标准：每点1分，若超过字数，该点不得分，共4分。

）4．爸爸：妈妈来电话说消费税调整，车要涨价，请您今天带订单去经销商处提车。

芳芳3月25日（评分标准：称谓1分、署名及时间1分，三句话各1分，共5分。

）二、文言文阅读5.（1）狱：案件（2）被：接受（3）晏：安定6．A （都是介词，把。

B项是介词，用……方式；C项是介词，凭……身份，D项是连词，表目的。

）7. B （“地方官员将大量百姓治罪，一度达到八百多人”有误，应该是“官吏中应被处以刑罚的有八百多人”。

）8. (1) 赵公独自掌管政事，却隐藏了事实的真相，使得那些决策好像不是出于自己之手。

（3分。

“左右”1分，“晦”1分，语意流畅1分）(2) 河朔一带连年大丰收，所以不能按照（规定的）人数完成招募，请（皇上）宽赦他们的罪，等农闲之时（再继续招募）。

（4分。

“频岁”1分，“如”1分，“俟”1分，语意流畅1分）(3) 谨慎施行法律，遵循规矩。