湖南省浏阳一中、攸县一中高三数学上学期期中联考试卷文

2016-2017学年湖南省浏阳一中、攸县一中高三（上）10月联考数学试卷（理科）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求）1．设集合M={x|2x﹣x2≥0}，N=，则M∩N等于（）A．（﹣1，0]B．[﹣1，0]C．[0，1） D．[0，1]2．“log2（2x﹣3）＜1”是“4x＞8”的（）A．充分不必要条件 B．必要不充分条件C．充分必要条件D．既不充分也不必要条件3．若tanθ=，则cos2θ=（）A．B．C．D．4．已知向量=（3，﹣2），=（x，y﹣1）且∥，若x，y均为正数，则+的最小值是（）A．24 B．8 C．D．5．设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：①若m⊥α，n∥α，则m⊥n②若α∥β，β∥γ，m⊥α，则m⊥γ③若m∥α，n∥α，则m∥n④若α⊥γ，β⊥γ，则α∥β其中正确命题的序号是（）A．①和②B．②和③C．③和④D．①和④6．若a=，则二项式（a﹣）6的展开式中含x项的系数是（）A．210 B．﹣210 C．240 D．﹣2407．函数f（x）为定义在R上的偶函数，且满足f（x+1）+f（x）=1，当x∈[1，2]时，f（x）=2﹣x，则f（﹣2013）=（）A．﹣1 B．1 C．2 D．﹣28．从0，1，2，3，4，5这六个数字中任取两个奇数和两个偶数，组成没有重复数字的四位数的个数为（）A．300 B．216 C．180 D．1629．点P是曲线y=x2﹣lnx上任意一点，则点P到直线y=x+2的最小距离为（）A．B．C．2 D．210．已知某几何体的三视图如图所示，则该几何体的表面积等于（）A． B．160 C．64+32D．88+811．已知函数，则关于a的不等式f（a﹣2）+f（a2﹣4）＜0的解集是（）A．B．（﹣3，2）C．（1，2） D．12．已知函数y=f（x）是定义域为R的偶函数．当x≥0时，f（x）=若关于x的方程[f（x）]2+af（x）+b=0（a，b∈R），有且仅有6个不同实数根，则实数a的取值范围是（）A．（﹣，﹣）B．（﹣，﹣1）C．（﹣，﹣）∪（﹣，﹣1）D．（﹣，﹣1）二、填空题（本大题共4小题，每小题5分，共20分．请将答案填在答题卷上）13．已知幂函数y=f（x）的图象过点，则=．14．已知矩形ABCD中，AB=2，AD=1，E、F分别是BC、CD的中点，则（）•等于．15．在棱长为1的正方体ABCD﹣A1B1C1D1中，E为AB1的中点，在面ABCD中取一点F，使EF+FC1最小，则最小值为．16．定义在（0，+∞）上的函数f（x）满足：①当x∈[1，3）时，f（x）=1﹣|x ﹣2|；②f（3x）=3f（x）．设关于x的函数F（x）=f（x）﹣a的零点从小到大依+x2n=．（用次为x1，x2，...，x n，...（n∈N*）．若a∈（1，3），则x1+x2+ (x2)﹣1n表示）三、解答题（本大题共6小题，共70分．解答应写出文字说明，演算步骤或证明过程）17．已知，且，（1）求cosα的值；（2）若，，求cosβ的值．18．已知向量，设函数f（x）=．（1）求f（x）在上的最值；（2）在△ABC中，a，b，c分别是角A，B，C的对边，若f（A）=4，b=1，△ABC的面积为，求a的值．19．如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD=DC=AP=2，AB=1，点E为棱PC的中点．（Ⅰ）证明：BE⊥DC；（Ⅱ）求直线BE与平面PBD所成角的正弦值；（Ⅲ）若F为棱PC上一点，满足BF⊥AC，求二面角F﹣AB﹣P的余弦值．20．某课题组对全班45名同学的饮食习惯进行了一次调查，并用茎叶图表示45名同学的饮食指数．说明：如图中饮食指数低于70的人被认为喜食蔬菜，饮食指数不低于70的人被认为喜食肉类（1）根据茎叶图，完成下面2×2列联表，并判断是否有90%的把握认为喜食蔬菜还是喜食肉类与性别有关，说明理由：（2）根据饮食指数在[10，39]，[40，69]，[70，99]进行分层抽样，从全班同学中抽取15名同学进一步调查，记抽取到的喜食肉类的女同学为ξ，求ξ的分布列和数学期望E ξ下面公式及临界值表仅供参考：附：X 2=21．一家公司计划生产某种小型产品的月固定成本为1万元，每生产1万件需要再投入2万元，设该公司一个月内生产该小型产品x万件并全部销售完，每万件的销售收入为4﹣x万元，且每万件国家给予补助2e﹣﹣万元．（e为自然对数的底数，e是一个常数）（Ⅰ）写出月利润f（x）（万元）关于月产量x（万件）的函数解析式（Ⅱ）当月产量在[1，2e]万件时，求该公司在生产这种小型产品中所获得的月利润最大值（万元）及此时的月生成量值（万件）．（注：月利润=月销售收入+月国家补助﹣月总成本）22．已知函数f（x）=ln（1+x2）+ax．（a≤0）（1）若f（x）在x=0处取得极值，求a的值；（2）讨论f（x）的单调性；（3）证明：（1+）（1+）…（1+）＜（n∈N*，e为自然对数的底数）．2016-2017学年湖南省浏阳一中、攸县一中高三（上）10月联考数学试卷（理科）参考答案与试题解析一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求）1．设集合M={x|2x﹣x2≥0}，N=，则M∩N等于（）A．（﹣1，0]B．[﹣1，0]C．[0，1） D．[0，1]【考点】交集及其运算．【分析】分别求出集合M，N，再利用交集定义求解．【解答】解：∵集合M={x|2x﹣x2≥0}={x|0≤x≤2}，N=={x|﹣1＜x＜1}，∴M∩N={x|0≤x＜1}=[0，1）．故选：C．2．“log2（2x﹣3）＜1”是“4x＞8”的（）A．充分不必要条件 B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】利用函数的单调性分别化简log2（2x﹣3）＜1，4x＞8，即可判断出结论．【解答】解：log2（2x﹣3）＜1，化为0＜2x﹣3＜2，解得．4x＞8，即22x＞23，解得x．∴“log2（2x﹣3）＜1”是“4x＞8”的充分不必要条件．故选：A．3．若tanθ=，则cos2θ=（）A．B．C．D．【考点】三角函数的化简求值．【分析】原式利用二倍角的余弦函数公式变形，再利用同角三角函数间的基本关系化简，将tanθ的值代入计算即可求出值．【解答】解：∵tanθ=，∴cos2θ=2cos2θ﹣1=﹣1=﹣1=．故选：D．4．已知向量=（3，﹣2），=（x，y﹣1）且∥，若x，y均为正数，则+的最小值是（）A．24 B．8 C．D．【考点】平面向量共线（平行）的坐标表示；基本不等式．【分析】根据向量共线定理列出方程，得出2x+3y=3，再求的最小值即可．【解答】解：∵∥，∴﹣2x﹣3（y﹣1）=0，化简得2x+3y=3，∴=（+）×（2x+3y）=（6+++6）≥（12+2）=8，当且仅当2x=3y=时，等号成立；∴的最小值是8．故选：B．5．设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：①若m⊥α，n∥α，则m⊥n②若α∥β，β∥γ，m⊥α，则m⊥γ③若m∥α，n∥α，则m∥n④若α⊥γ，β⊥γ，则α∥β其中正确命题的序号是（）A．①和②B．②和③C．③和④D．①和④【考点】空间中直线与平面之间的位置关系；命题的真假判断与应用；空间中直线与直线之间的位置关系；平面与平面之间的位置关系．【分析】根据线面平行性质定理，结合线面垂直的定义，可得①是真命题；根据面面平行的性质结合线面垂直的性质，可得②是真命题；在正方体中举出反例，可得平行于同一个平面的两条直线不一定平行，垂直于同一个平面和两个平面也不一定平行，可得③④不正确．由此可得本题的答案．【解答】解：对于①，因为n∥α，所以经过n作平面β，使β∩α=l，可得n∥l，又因为m⊥α，l⊂α，所以m⊥l，结合n∥l得m⊥n．由此可得①是真命题；对于②，因为α∥β且β∥γ，所以α∥γ，结合m⊥α，可得m⊥γ，故②是真命题；对于③，设直线m、n是位于正方体上底面所在平面内的相交直线，而平面α是正方体下底面所在的平面，则有m∥α且n∥α成立，但不能推出m∥n，故③不正确；对于④，设平面α、β、γ是位于正方体经过同一个顶点的三个面，则有α⊥γ且β⊥γ，但是α⊥β，推不出α∥β，故④不正确．综上所述，其中正确命题的序号是①和②故选：A6．若a=，则二项式（a﹣）6的展开式中含x项的系数是（）A．210 B．﹣210 C．240 D．﹣240【考点】二项式系数的性质．【分析】利用定积分求出n，利用二项展开式的通项公式求出通项，令x的指数等于1，求出系数即可．【解答】解：a==﹣cosx=2∴（a﹣）6=（2﹣）6展开式的通项为T r+1=（﹣1）r26﹣r C6r x3﹣r令3﹣r=1得r=2，故展开式中含x项的系数是16C62=240故选C．7．函数f（x）为定义在R上的偶函数，且满足f（x+1）+f（x）=1，当x∈[1，2]时，f（x）=2﹣x，则f（﹣2013）=（）A．﹣1 B．1 C．2 D．﹣2【考点】函数的周期性；抽象函数及其应用；函数的值．【分析】利用函数f（x）为定义在R上的偶函数，且满足f（x+1）+f（x）=1，可求得f（x+2）=f（x），再结合x∈[1，2]时f（x）=2﹣x，即可求得答案．【解答】解：∵f（x+1）+f（x）=1，①用﹣x代替x得：f（﹣x+1）+f（﹣x）=1，②∵f（x）为定义在R上的偶函数，f（﹣x）=f（x），∴②式可化为：f（﹣x+1）+f（x）=1③由①③得：f（x+1）=f（1﹣x），∴f[（x+1）+1]=f[1﹣（x+1）]=f（﹣x）=f（x），即f（x+2）=f（x），∴f（x）是以2为周期的函数，又f（x）为定义在R上的偶函数，又x∈[1，2]时f（x）=2﹣x，∴f（﹣2013）=f=2﹣1=1，故选B．8．从0，1，2，3，4，5这六个数字中任取两个奇数和两个偶数，组成没有重复数字的四位数的个数为（）A．300 B．216 C．180 D．162【考点】排列、组合的实际应用．【分析】本题是一个分类计数原理，从1，2，3，4，5中任取两个奇数和两个偶数，组成没有重复数字的四位数；取0此时2和4只能取一个，0不可能排在首位，组成没有重复数字的四位数的个数为C32C21[A44﹣A33]，根据加法原理得到结果．【解答】解：由题意知，本题是一个分类计数原理，第一类：从1，2，3，4，5中任取两个奇数和两个偶数，组成没有重复数字的四位数的个数为C32A44=72第二类：取0，此时2和4只能取一个，0不能排在首位，组成没有重复数字的四位数的个数为C32C21[A44﹣A33]=108∴组成没有重复数字的四位数的个数为108+72=180故选C．9．点P是曲线y=x2﹣lnx上任意一点，则点P到直线y=x+2的最小距离为（）A．B．C．2 D．2【考点】利用导数研究曲线上某点切线方程．【分析】求出平行于直线y=x+2且与曲线y=x2﹣lnx相切的切点坐标，再利用点到直线的距离公式可得结论．【解答】解：设P（x，y），则y′=2x﹣（x＞0）令2x﹣=1，则（x﹣1）（2x+1）=0，∵x＞0，∴x=1，∴y=1，即平行于直线y=x+2且与曲线y=x2﹣lnx相切的切点坐标为（1，1）．由点到直线的距离公式可得d==．故选：B．10．已知某几何体的三视图如图所示，则该几何体的表面积等于（）A． B．160 C．64+32D．88+8【考点】由三视图求面积、体积．【分析】由已知中的三视图，我们可以判断该几何体是由一个直三棱柱去掉一个三棱锥组成，然后根据相应的长度即可求该几何体的表面积．【解答】解：由三视图可知该几何体是由一个直三棱柱去掉一个三棱锥组成，三棱柱的底面是一个直角边长为4的直角三角形，高为8，即AD=DE=4，AB=8，FH=4，∴CF=，AE=，∴该几何体的表面积为==64+，故选：C．11．已知函数，则关于a的不等式f（a﹣2）+f（a2﹣4）＜0的解集是（）A．B．（﹣3，2）C．（1，2） D．【考点】奇偶性与单调性的综合．【分析】根据已知中的函数解析式，先分析函数的单调性和奇偶性，进而根据函数的性质及定义域，可将不等式f（a﹣2）+f（a2﹣4）＜0化为1＞a﹣2＞4﹣a2＞﹣1，解不等式组可得答案．【解答】解：函数的定义域为（﹣1，1）∵f（﹣x）=﹣sinx=﹣f（x）∴函数f（x）为奇函数又∵f′（x）=+cosx＞0，∴函数在区间（﹣1，1）上为减函数，则不等式f（a﹣2）+f（a2﹣4）＜0可化为：f（a﹣2）＜﹣f（a2﹣4）即f（a﹣2）＜f（4﹣a2），即1＞a﹣2＞4﹣a2＞﹣1解得＜a＜2故关于a的不等式f（a﹣2）+f（a2﹣4）＜0的解集是（，2）．故选：A．12．已知函数y=f（x）是定义域为R的偶函数．当x≥0时，f（x）=若关于x的方程[f（x）]2+af（x）+b=0（a，b∈R），有且仅有6个不同实数根，则实数a的取值范围是（）A．（﹣，﹣）B．（﹣，﹣1）C．（﹣，﹣）∪（﹣，﹣1）D．（﹣，﹣1）【考点】分段函数的应用；根的存在性及根的个数判断．【分析】根据函数的奇偶性作出函数f（x）的图象，利用换元法判断函数t=f（x）的根的个数，利用数形结合即可得到结论．【解答】解：作出函数f（x）的图象如图：则f（x）在（﹣∞，﹣1）和（0，1）上递增，在（﹣1，0）和（1，+∞）上递减，当x=±1时，函数取得极大值f（1）=；当x=0时，取得极小值0．要使关于x的方程[f（x）]2+af（x）+b=0，a，b∈R有且只有6个不同实数根，设t=f（x），则当t＜0，方程t=f（x），有0个根，当t=0，方程t=f（x），有1个根，当0＜t≤1或t=，方程t=f（x），有2个根，当1＜t＜，方程t=f（x），有4个根，当t＞，方程t=f（x），有0个根．则t2+at+b=0必有两个根t1、t2，则有两种情况符合题意：①t1=，且t2∈（1，），此时﹣a=t1+t2，则a∈（﹣，﹣）；②t1∈（0，1]，t2∈（1，），此时同理可得a∈（﹣，﹣1），综上可得a的范围是（﹣，﹣）∪（﹣，﹣1），故选：C二、填空题（本大题共4小题，每小题5分，共20分．请将答案填在答题卷上）13．已知幂函数y=f（x）的图象过点，则=1．【考点】幂函数的概念、解析式、定义域、值域．【分析】设幂函数y=f（x）=xα（α为常数），由图象过点，则，解得α，再利用对数的运算性质即可得出．【解答】解：设幂函数y=f（x）=xα（α为常数），由图象过点，则，解得α=．∴f（x）=，∴f（4）=2．=log22=1．故答案为：1．14．已知矩形ABCD中，AB=2，AD=1，E、F分别是BC、CD的中点，则（）•等于．【考点】平面向量数量积的运算．【分析】利用向量的运算法则和数量积的定义即可得出．【解答】解：如图所示，∵矩形ABCD中，E、F分别是BC、CD的中点，∴=，．∴（）•=====．故答案为．15．在棱长为1的正方体ABCD﹣A1B1C1D1中，E为AB1的中点，在面ABCD中取一点F，使EF+FC1最小，则最小值为．【考点】棱柱的结构特征．【分析】由题意，作出点E关于面ABCD的对称点E′，连C1E′交面ABCD于点F，则C1E′的长即为所求．【解答】解：由题意，作出点E关于面ABCD的对称点E′，连C1E′交面ABCD于点F，则C1E′的长即为所求．∵E是AB1的中点，∴C1E′==．∴EF+FC1的最小值为．故答案为：．16．定义在（0，+∞）上的函数f（x）满足：①当x∈[1，3）时，f（x）=1﹣|x ﹣2|；②f（3x）=3f（x）．设关于x的函数F（x）=f（x）﹣a的零点从小到大依+x2n=6（3n 次为x1，x2，...，x n，...（n∈N*）．若a∈（1，3），则x1+x2+ (x2)﹣1﹣1）．（用n表示）【考点】分段函数的应用．【分析】根据分段函数的表达式，作出函数的图象，利用数形结合确定零点的取值关系，利用数列求和的公式即可得到结论．【解答】解：由①当x∈[1，3）时，，可画出f（x）在[1，3）上的图象，根据②f（3x）=3f（x），只要将f（x）在[1，3）上的图象沿x轴伸长到原来的3倍，再沿y轴伸长到原来的3倍即可得到f（x）在[3，9）上的图象，以此类推，可得到在[9，27），[27，81）…上的图象，关于x的函数F（x）=f（x）﹣a的零点，可看成函数y=f（x）与y=a图象交点的横坐标，由函数y=f（x）图象的对称性可知：如图，所以就有，因此三、解答题（本大题共6小题，共70分．解答应写出文字说明，演算步骤或证明过程）17．已知，且，（1）求cosα的值；（2）若，，求cosβ的值．【考点】二倍角的余弦；同角三角函数间的基本关系；两角和与差的正弦函数．【分析】（1）把已知条件平方可得sinα=，再由已知，可得cosα的值．（2）由条件可得﹣＜α﹣β＜，cos（α﹣β）=，再根据cosβ=cos（﹣β）=cos[（α﹣β ）﹣α]，利用两角和差的余弦公式，运算求得结果．【解答】解：（1）由，平方可得1+sinα=，解得sinα=．再由已知，可得α=，∴cosα=﹣．（2）∵，，∴﹣＜α﹣β＜，cos（α﹣β）=．∴cosβ=cos（﹣β）=cos[（α﹣β ）﹣α]=cos（α﹣β）cosα+sin（α﹣β）sinα=+=﹣．18．已知向量，设函数f（x）=．（1）求f（x）在上的最值；（2）在△ABC中，a，b，c分别是角A，B，C的对边，若f（A）=4，b=1，△ABC的面积为，求a的值．【考点】平面向量数量积的运算．【分析】（1）由已知结合数量积的坐标表示求得f（x），得到f（x）在上的单调性，从而求得最值；（2）由f（A）=4求得角A，然后结合正弦定理和余弦定理求得a值．【解答】解：（1）∵=，∴f（x）在上单调递增，在上单调递减，又，∴f（x）min=4，f（x）max=5；（2）∵，∴，∵∈（），∴，则A=，∵，∴c=2，则a2=b2+c2﹣2bccosA=3，∴a=．19．如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD=DC=AP=2，AB=1，点E为棱PC的中点．（Ⅰ）证明：BE⊥DC；（Ⅱ）求直线BE与平面PBD所成角的正弦值；（Ⅲ）若F为棱PC上一点，满足BF⊥AC，求二面角F﹣AB﹣P的余弦值．【考点】与二面角有关的立体几何综合题；直线与平面所成的角．【分析】（I）以A为坐标原点，建立如图所示的空间直角坐标系，求出BE，DC的方向向量，根据•=0，可得BE⊥DC；（II）求出平面PBD的一个法向量，代入向量夹角公式，可得直线BE与平面PBD 所成角的正弦值；（Ⅲ）根据BF⊥AC，求出向量的坐标，进而求出平面FAB和平面ABP的法向量，代入向量夹角公式，可得二面角F﹣AB﹣P的余弦值．【解答】证明：（I）∵PA⊥底面ABCD，AD⊥AB，以A为坐标原点，建立如图所示的空间直角坐标系，∵AD=DC=AP=2，AB=1，点E为棱PC的中点．∴B（1，0，0），C（2，2，0），D（0，2，0），P（0，0，2），E（1，1，1）∴=（0，1，1），=（2，0，0）∵•=0，∴BE⊥DC；（Ⅱ）∵=（﹣1，2，0），=（1，0，﹣2），设平面PBD的法向量=（x，y，z），由，得，令y=1，则=（2，1，1），则直线BE与平面PBD所成角θ满足：sinθ===，故直线BE与平面PBD所成角的正弦值为．（Ⅲ）∵=（1，2，0），=（﹣2，﹣2，2），=（2，2，0），由F点在棱PC上，设=λ=（﹣2λ，﹣2λ，2λ）（0≤λ≤1），故=+=（1﹣2λ，2﹣2λ，2λ）（0≤λ≤1），由BF⊥AC，得•=2（1﹣2λ）+2（2﹣2λ）=0，解得λ=，即=（﹣，，），设平面FBA的法向量为=（a，b，c），由，得令c=1，则=（0，﹣3，1）， 取平面ABP 的法向量=（0，1，0）， 则二面角F ﹣AB ﹣P 的平面角α满足： cosα===，故二面角F ﹣AB ﹣P 的余弦值为：20．某课题组对全班45名同学的饮食习惯进行了一次调查，并用茎叶图表示45名同学的饮食指数．说明：如图中饮食指数低于70的人被认为喜食蔬菜，饮食指数不低于70的人被认为喜食肉类（1）根据茎叶图，完成下面2×2列联表，并判断是否有90%的把握认为喜食蔬菜还是喜食肉类与性别有关，说明理由：（2）根据饮食指数在[10，39]，[40，69]，[70，99]进行分层抽样，从全班同学中抽取15名同学进一步调查，记抽取到的喜食肉类的女同学为ξ，求ξ的分布列和数学期望E ξ下面公式及临界值表仅供参考：附：X 2=【考点】独立性检验的应用；极差、方差与标准差．【分析】（Ⅰ）根据统计数据，可得2×2列联表，根据列联表中的数据，计算K2的值，即可得到结论；（Ⅱ）ξ的可能取值有0，1，2，3，求出相应的概率，可得ξ的分布列及数学期望．【解答】解：（1）根据茎叶图，填写2×2列联表，如下；计算观测值K2==0.5625＜2.706；对照数表得出，没有90%的把握认为喜食蔬菜还是喜食肉类与性别有关；（2）因为从喜食肉类同学中抽取9×=3人，所以ξ可能取值有0，1，2，3．P（ξ=0）==，P（ξ=1）==，P（ξ=2）==，P（ξ=3）==．所以ξ的分布列是所以ξ的期望值是Eξ=0×+1×+2×+3×=1．21．一家公司计划生产某种小型产品的月固定成本为1万元，每生产1万件需要再投入2万元，设该公司一个月内生产该小型产品x万件并全部销售完，每万件的销售收入为4﹣x万元，且每万件国家给予补助2e﹣﹣万元．（e为自然对数的底数，e是一个常数）（Ⅰ）写出月利润f（x）（万元）关于月产量x（万件）的函数解析式（Ⅱ）当月产量在[1，2e]万件时，求该公司在生产这种小型产品中所获得的月利润最大值（万元）及此时的月生成量值（万件）．（注：月利润=月销售收入+月国家补助﹣月总成本）【考点】导数在最大值、最小值问题中的应用．【分析】（Ⅰ）由月利润=月销售收入+月国家补助﹣月总成本，即可列出函数关系式；（2）利用导数判断函数的单调性，进而求出函数的最大值．【解答】解：（Ⅰ）由于：月利润=月销售收入+月国家补助﹣月总成本，可得（Ⅱ）f（x）=﹣x2+2（e+1）x﹣2elnx﹣2的定义域为[1，2e]，且列表如下：由上表得：f（x）=﹣x2+2（e+1）x﹣2elnx﹣2在定义域[1，2e]上的最大值为f （e）．且f（e）=e2﹣2．即：月生产量在[1，2e]万件时，该公司在生产这种小型产品中所获得的月利润最大值为f（e）=e2﹣2，此时的月生产量值为e（万件）．22．已知函数f（x）=ln（1+x2）+ax．（a≤0）（1）若f（x）在x=0处取得极值，求a的值；（2）讨论f（x）的单调性；（3）证明：（1+）（1+）…（1+）＜（n∈N*，e为自然对数的底数）．【考点】利用导数研究函数的极值；利用导数研究函数的单调性；不等式的证明．【分析】（1）求出f′（x），因为f（x）在x=0时取得极值，所以f'（0）=0，代入求出a即可；（2）分三种情况：a=0；a≤﹣1；﹣1＜a＜0，令f′（x）＞0得到函数的递增区间；令f′（x）＜0得到函数的递减区间即可；（3）由（2）知当a=﹣1时函数为减函数，所以得到ln（1+x2）＜x，利用这个结论根据对数的运算法则化简不等式的左边得证即可．【解答】解：（1）∵，∵x=0使f（x）的一个极值点，则f'（0）=0，∴a=0，验证知a=0符合条件．（2）∵①若a=0时，∴f（x）在（0，+∞）单调递增，在（﹣∞，0）单调递减；②若得，当a≤﹣1时，f'（x）≤0对x∈R恒成立，∴f（x）在R上单调递减．③若﹣1＜a＜0时，由f'（x）＞0得ax2+2x+a＞0∴再令f'（x）＜0，可得∴上单调递增，在综上所述，若a≤﹣1时，f（x）在（﹣∞，+∞）上单调递减；若﹣1＜a＜0时，上单调递增上单调递减；若a=0时，f（x）在（0，+∞）单调递增，在（﹣∞，0）单调递减．（3）由（2）知，当a=﹣1时，f（x）在（﹣∞，+∞）单调递减当x∈（0，+∞）时，由f（x）＜f（0）=0∴ln（1+x2）＜x，∴ln[（1+）（1+）…（1+）]=ln（1+）+ln（1+）+…+ln（1+）＜++…+==（1﹣）＜，∴（1+）（1+）…（1+）＜=2017年1月18日。

2016届高三浏阳一中、攸县一中十一月联考文科数学试卷时量：120分钟 总分：150分 命题人：邹辉煌 审题人：黄六合一．选择题（本大题共有12个小题，每小题5分，共60分） 1．设集合{|lg(2)}A x y x ==-，集合{|22}B x x =-≤≤，则A B = （ ）A ．{|2}x x ≥-B ．{|22}x x -<<C ．{|22}x x -≤<D ．{|2}x x <2.在复平面内复数 121iz i+=-对应的点在( )A.第一象限B.第二象限C.第三象限D.第四象限3．已知命题p ：若x∈R，则21≥+xx ，命题q ：若0)1(1≥-x g ，则x≥2，则下列各命题中是假命题的是（ ）A ．q p ∨B ．q p ∨⌝)(C ．q p ∧⌝)(D ．)()(q p ⌝∧⌝ 4.平面向量与的夹角为60°，=(2,0)，||=1，则|+2|等于（ ）A. 32B. 22C. 4D. 105．若110a b <<，则下列不等式：①a b <； ②||||a b >；③a b ab +<；④2b a a b+>中，正确的不等式有( )A.①②B. .①④ C ．②③D.③④5. 若函数()f x 为定义在R 上的偶函数，最小正周期为π，且当0,2x π⎡⎤∈⎢⎥⎣⎦时，()sin f x x =，则5()3f π的值为( )A ．12- B ．12 C．7.在△ABC中，已知030,8,A a b ===，则三角形的面积为（ ） A．．16 C．或16 D．或8.设{}n a 是公差不为零的等差数列，22a =．且139,,a a a 成等比数列，则数列 {}n a 的前n 项n S =( ) A.2744n n+ B.2322n n+ C.2344n n+ D. 222n n+9.ABC ∆中，点E 为AB 边的中点，点F 为边AC 的中点，BF 交CE 于点G ，若若y x +=，则x+y 等于( )A. 32B.1C. 43D. 2310、函数()()sin f x A x ωϕ=+（其中0,2A πϕ><）的图像如图所示，为了得到()sin2g x x =的图像，则只需将()f x 的图像( )（A ）向左平移3π个长度单位 （B ）向右平移3ππ7πx个长度单位（C ）向左平移6π个长度单位 （D ）向右平移6π个长度单位11. 已知函数⎪⎩⎪⎨⎧≥-<≤+=)1(212)10(1)(x x x x f x ，设0≥>b a ，若f(a)=f(b)，则)(a f b ∙的取值范围是( )A ．】，（21B ．】，（243 C ．），【243 D ．），（22112.设()f x 与()g x 是定义在同一区间[],a b 上的两个函数，若函数()()[],y f x g x x a b =-∈在上有两个不同的零点，则称()f x 和()g x 在[],a b 上是“关联函数”，区间[],a b 称为“关联区间”。

湖南省浏阳一中、攸县一中、醴陵一中2015届高三数学上学期12月联考试题 文本卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试用时120分钟 一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的1、设全集(2),{|21},{|ln(1)}x x U R A x B x y x -==<==-，则图中阴影部分表示的集合为 A ．{}|1x x ≥ B ．{}|1x x ≤ C ．{}|01x x <≤ D ．{}21<≤x x 2、已知()3sin f x x x π=-，命题():(0,),02p x f x π∀∈<，则A ．p 是真命题，():(0,),02p x f x π⌝∀∈>B ．p 是真命题，p ┐： ()000,,02x f x π⎛⎫∃∈≥ ⎪⎝⎭C ．p 是假命题，():(0,),02p x f x π⌝∀∈≥D ．p 是假命题，p ┐： ()000,,02x f x π⎛⎫∃∈≥ ⎪⎝⎭3、定义在R 上的函数()f x 满足()()()(),22f x f x f x f x -=--=+，且(1,0)x ∈-时，()125x f x =+，则()2log 20f =A ．1B ．45C ．1-D ．45-4、某产品在某零售摊位的零售价x （单位：元）与每天的销售量y （单位：个）的统计资料如下表所示：由上表可得回归直线方程ˆˆˆybx a =+中的ˆ4b =-，据此模型预测零售价 为15元时，每天的销售量为A ．51个B ．50个C ．49个D ．48个5、设等比数列{a n }的前n 项和为S n .若S 2＝3，S 4＝15，则S 6＝( )A ．31B ．32C ．63D ．646、已知函数()322,()2,03a f x x ax cx g x ax ax c a =++=++≠，则它们的图象可能是7、已知函数()sin()(0)4f x x πωω=+>的最小正周期为π，则该函数的图象是A ．关于直线8x π=对称 B ．关于点(,0)4π对称 C ．关于直线4x π=对称 D ．关于点(,0)8π对称8、一只受伤的丹顶鹤在如图所示（直角梯形）的草原上飞过，其中2,1AD DC BC ===，它可能随机在草原上任何一 处（点），若落在扇形沼泽区域ADE 以外丹顶鹤能生还， 则该丹顶鹤生还的概率是（ ） A ．1215π- B ．110π- C ．16π- D ．3110π- 9、已知函数()y f x =对于任意的(,)22x ππ∈-满足()()cos sin 0f x x f x x '+>（其中()f x '是函数()f x 的导函数），则下列不等式不成立的是（ ）A ()()34f ππ< B ．()()34f ππ-<-C ．(0)()4f π<D ． (0)2()3f f π<10、已知函数()32(,f x x bx cx d bc d =+++均为常数)，当(0,1)x ∈时取极大值，当(1,2)x ∈时取极小值，则221()(3)2b c ++-的取值范围是A ．2B ．)C ．37(,25)4D ．()5,25二、填空题：本大题共5小题，每小题5分，共25分，把答案填在题中的横线上 11、若不等式131x x m ++-≥-恒成立，则实数m 的取值范围是12、定义行列式的运算:12122112a a ab a b b b =-，若将函数()sin cos xf x x=的图象向左平移(0)t t >个单位，所得图象对应的函数为偶函数，则t 的最小值为13、设曲线2cos sin x y x -=在点(,2)2π处切线与直线10x ay ++=垂直，则a =14、已知命题:p 函数()22lg(4)f x x x a =-+的定义域为R ；命题:q [1,1]m ∀∈-，不等式253a a --≥p q ∨“为真命题，且“p q ∧”为假命题，则实数a 的取值范围是15、已知函数()2xf x e x a =-+有零点，则a 的取值范围是三、解答题：本大题共6小题，共75分，解答应写成文字说明、证明过程或演算步骤 16、（本小题满分12分）已知幂函数223()()m m f x x m z -++=∈为偶函数，且在区间(0,)+∞上是单调增函数（1）求函数()f x 的解析式； （2）设函数3219()()()42g x f x ax x b x R =++-∈，其中,a b R ∈.若函数()g x 仅在0x =处有极值，求a 的取值范围.17. （本小题满分12分）已知函数()sin f x m x x =+,(0)m >的最大值为2． （Ⅰ）求函数()f x 在[]0,π上的值域； (Ⅱ)已知ABC ∆外接圆半径3=R，()()sin 44f A f B A B ππ-+-=，角,A B 所对的边分别是,a b ，求11+的值． 分）已知数列的前项和求的通项公式；，求数列的前项和．19. （本小题满分12分） 如图，在四棱锥P ABCD -中，90ABC ACD ∠=∠=︒,60BAC CAD ∠=∠=︒, PA ⊥平面ABCD ,E 为PD 的中点，22PA AB ==.(I ) 求证：CE ∥平面PAB ; ( II ) 求四面体PACE 的体积.20. （本小题满分13分） 已知椭圆C 的对称中心为原点O ，焦点在x 轴上，左右焦点分别为1F 和2F ，且|1F 2F |=2，点（1，23）在该椭圆上． （1）求椭圆C 的方程；（2）过1F 的直线l 与椭圆C 相交于A ，B 两点，若∆A 2F B 的面积为7212，求以2F 为圆心且与直线l 相切圆的方程．21.（本小题满分14分）.已知函数x x x f ln )(=，x e ax x x g )3()(2-+-=（a 为实数）． (Ⅰ) 当a=5时，求函数)(x g y =在1=x 处的切线方程； (Ⅱ) 求)(x f 在区间[t ，t+2]（t >0）上的最小值；(Ⅲ) 若存在两不等实根]1[，21，e ex x ∈，使方程)(2)(x f e x g x =成立，求实数a 的取值范围．浏攸醴11月高三文科数学考试答案一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中， 只有一项是符合题目要求的.1. D【解析】因为图中阴影部分表示的集合为()U A C B ，由题意可知{}{}02,1A x x B x x =<<=<，所以()U A C B {}{}021x x x x =<<≥ {}12x x =≤<，故选.D2. B【解析】依题意得，当0,2x π⎛⎫∈ ⎪⎝⎭时，()3cos 30f x x ππ'=-<-<，函数()f x 是减函数，此时()()03sin000f x f π<=-⨯=，即有()0f x <恒成立，因此命题p 是真命题，p ┐应是“()000,,02x f x π⎛⎫∃∈≥ ⎪⎝⎭”.综上所述，应选.B3. C【解析】由()()()()224f x f x f x f x -=+⇒=+，因为24log 205<<，所以20log 2041<-<，214log 200-<-<，所以 ()()()22224log 20log 2044log 20log 15f f f f ⎛⎫=-=--=-=- ⎪⎝⎭.故选.C4. C【解析】由题意知17.5,39x y ==，代入回归直线方程得 109,a=109154-⨯49=，故选.C5. C [解析] 设等比数列{a n }的首项为a ，公比为q ，易知q ≠1，根据题意可得⎩⎪⎨⎪⎧a （1－q 2）1－q ＝3，a （1－q 4）1－q ＝15，解得q 2＝4，a 1－q ＝－1，所以S 6＝a （1－q 6）1－q ＝(－1)(1－43)＝63. 6. B【解析】因为()22f x ax ax c '=++，则函数()f x '即()g x 图象的对称轴为1x =-，故可排除,A D ；由选项C 的图象可知，当0x >时，()0f x '>，故函数()323a f x x ax cx =++在()0,+∞上单调递增，但图象中函数()f x 在()0,+∞上不具有单调性，故排除.C 本题应选.B7.A【解析】依题意得2,2T ππωω===，故()sin 24f x x π⎛⎫=+ ⎪⎝⎭，所以 sin 2sin 108842f ππππ⎛⎫⎛⎫=⨯+==≠ ⎪ ⎪⎝⎭⎝⎭，sin 2444f πππ⎛⎫⎛⎫=⨯+ ⎪ ⎪⎝⎭⎝⎭3sin4π==0≠，因此该函数的图象关于直线8x π=对称，不关于点,04π⎛⎫⎪⎝⎭和点,08π⎛⎫⎪⎝⎭对称，也不关于直线4x π=对称.故选.A8. B【解析】过点D 作DF AB ⊥于点F ，在Rt AFD ∆中，易知1,45AF A =∠= ，梯形的面积()115221122S =++⨯=,扇形ADE的面积221244S ππ=⨯⨯=，则丹顶鹤生还的概率12152415102S S P S ππ--===-，故选.B9.A 10. D【解析】因为()232f x x bx c '=++，依题意，得()()()00,1230,24120,f c f b c f b c '=>⎧⎪'=++<⎨⎪'=++>⎩则点(),b c 所满足的可行域如图所示（阴影部分，且不包括边界），其中()4.5,6A -，()3,0B -，()1.5,0D -.()22132T b c ⎛⎫=++- ⎪⎝⎭表示点(),b c 到点1,32P ⎛⎫- ⎪⎝⎭的距离的平方，因为点P到直线AD 的距离d ==，观察图形可知，22d T PA<<，又()22214.563252PA ⎛⎫=-++-= ⎪⎝⎭，所以525T <<，故选.D二、填空题：（5题，每题5分） 11. []3,5-【解析】由于()()13134x x x x ++-≥+--=，则有14m -≤，即414m -≤-≤，解得35m -≤≤，故实数m 的取值范围是[]3,5-.12.56π 【解析】()sin 2cos 6f x x x x π⎛⎫=-=+⎪⎝⎭，平移后得到函数 2cos 6y x t π⎛⎫=++ ⎪⎝⎭，则由题意得,,66t k t k k Z ππππ+==-∈，因为0t >，所以t 的最小值为56π. 13.1【解析】由题意得()()()222cos sin 2cos sin 12cos sin sin x x x x x y xx''----'==，在点,22π⎛⎫⎪⎝⎭处的切线的斜率1212cos2 1.sin 2k ππ-==又该切线与直线10x ay ++=垂直，直线10x ay ++=的斜率21k a=-， 由121k k =-，解得 1.a =14. []()2,12,6--【解析】若命题p 为真，则216402a a ∆=-<⇒>或2a <-.若命题q 为真，因为[]1,1m ∈-，⎡⎤⎣⎦.因为对于[]1,1m ∀∈-，不等式253a a --≥恒成立，只需满足2533a a --≥，解得6a ≥或1a ≤-.命题“p q ∨”为真命题，且“p q ∧”为假命题，则,p q 一真一假.①当p 真q 假时，可得22,2616a a a a ><-⎧⇒<<⎨-<<⎩或；②当p q 假真时，可得22,2116a a a a -≤≤⎧⇒-≤≤-⎨≤-≥⎩或.综合①②可得a 的取值范围是[]()2,12,6-- . 15. (],22ln 2-∞-+【解析】由()20xf x e '=-=，解得ln 2.x =当(),ln 2x ∈-∞时，()0f x '<，函数()f x 单调递减； 当()ln 2,x ∈+∞时，()0f x '>，函数()f x 单调递增. 故该函数的最小值为()ln2ln22ln222ln2.f ea a =-+=-+因为该函数有零点，所以()ln 20f ≤，即22ln 20a -+≤，解得22ln 2.a ≤-+ 故a 的取值范围是(],22ln 2-∞-+. 16.【答案】（1）4()f x x = （2）[2,2]a ∈-（1）()f x 在区间(0,)+∞上是单调增函数，2230m m ∴-++>即2230m m --<13,m ∴-<<又,0,1,2m z m ∈∴=…………………4分 而0,2m =时，3()f x x =不是偶函数，1m =时，4()f x x =是偶函数，4()f x x ∴=. …………………………………………6分（2）2'()(39),g x x x ax =++显然0x =不是方程2390x ax ++=的根.为使()g x 仅在0x =处有极值，必须2390x ax ++≥恒成立，…………………8分 即有29360a ∆=-≤，解不等式，得[]2,2a ∈-.…………………11分这时，(0)g b =-是唯一极值. ∴[]2,2a ∈-. ……………12分17.解：（1）由题意，()f x．………………………2分而0m >，于是m =π()2sin()4f x x =+．…………………………………4分在]4,0[π上递增．在 ππ4⎡⎤⎢⎥⎣⎦，递减，所以函数()f x 在[]0π，上的值域为]2,2[-；…………………………………5分（2）化简ππ()()sin 44f A f B A B -+-=得sin sin sin A B A B +=． (7)分由正弦定理，得()2R a b +=，……………………………………………9分 因为△ABC 的外接圆半径为3=R．a b +=．…………………………11分 所以211=+ba …………………………………………………………………12分 18. 解：(Ⅰ) 由 ①可得：．同时②②-①可得：．——4分从而为等比数列，首项，公比为．． ————————6分(Ⅱ) 由(Ⅰ)知，————8分故．——12分19、答案：1)法一： 取AD 得中点M ，连接EM,CM.则EM//PA 因为,,EM PAB PA PAB ⊄⊂平面平面所以，//EM PAB 平面 （2分）MEPDBA在Rt ACD 中，60,CAD CM AM ∠=︒= 所以，60ACM ∠=︒而60BAC ∠=︒,所以,MC//AB. （3分） 因为,,MC PAB AB PAB ⊄⊂平面平面 所以，//MC PAB 平面 （4分） 又因为EM MC M = 所以，//EMC PAB 平面平面因为,//EC EC PAB ⊂平面EMC 所以，平面 （6法二： 延长DC,AB,交于N 点，连接PN. 因为60,NAC DAC AC CD ∠=∠=︒⊥ 所以，C 为ND 的中点. （3分） 因为E 为PD 的中点，所以，EC//PN 因为,,EC PAB PN PAB ⊄⊂平面平面//EC PAB 所以，平面 （6分）2)法一：由已知条件有;AC=2AB=2,AD=2AC=4,CD=（7分） 因为，PA ABCD ⊥平面，所以，PA CD ⊥ （8分）又因为,CD AC AC PA A ⊥= ，所以， CD PAC ⊥平面 （10分） 因为E 是PD 的中点，所以点E 平面PAC 的距离12h CD == 12222PAC S =⨯⨯= 所以，四面体PACE 的体积112333PAC V S h =⨯=⨯=（12分） 法二：由已知条件有;AC=2AB=2,AD=2AC=4,CD=因为，PA ABCD ⊥平面，所以，112333P ACD ACD V S PA -=⨯=⨯⨯=（10分）ND因为E 是PD 的中点，所以，四面体PACE的体积12P ACD V V -== （12分） 20.（1）椭圆C 的方程为13422=+y x ……………．．（4分） （2）①当直线l ⊥x 轴时，可得A （-1，-23），B （-1，23），∆A 2F B 的面积为3，不符合题意． …………（6分） ②当直线l 与x 轴不垂直时，设直线l 的方程为y=k （x+1）．代入椭圆方程得：01248)43(2222=-+++k x k x k ，显然∆＞0成立，设A ),(11y x ，B ),(22y x ，则2221438k k x x +-=+，222143128k k x x +-=⋅，可得|AB|=2243)1(12kk ++ ……………．．（9分） 又圆2F 的半径r=21||2k k +，∴∆A 2F B 的面积=21|AB| r=22431||12k k k ++=7212，化简得：174k +2k -18=0，得k=±1，∴r =2，圆的方程为2)1(22=+-y x ……………．．（13分）21.解:(Ⅰ)当5a =时2()(53)x g x x x e =-+-⋅,(1)g e =. ………1分 2()(32)x g x x x e '=-++⋅，故切线的斜率为(1)4g e '=. ………2分 所以切线方程为:4(1)y e e x -=-,即43y ex e =-. ………4分 (Ⅱ)()ln 1f x x '=+,………6分 ①当et 1≥时,在区间(,2)t t +上()f x 为增函数,7分,(9分a分hh14分。

2016下学期 浏阳一中高三年级期中测试卷文 科 数 学时量： 120分钟 分值：150分一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.若集合{|0}1xA x x =≤-,2{|2}B x x x =<,则A B = （ ）A.{|01}x x <<B.{|01}x x ≤<C.{|01}x x <≤D.{|01}x x ≤≤ 2.已知复数12312z bi z i =-=-，,若12z z 是实数，则实数b 的值为 （ ）A ．0B ．32-C ．6-D ．63. 在平面直角坐标系中，不等式组0401x y x y x +≥⎧⎪-+≥⎨⎪≤⎩表示的平面区域面积是（ ）．A ．9B ．6C ．92D ．3 4. 执行如图所示的程序框图，若输入如下四个函数：①()sin f x x =，②()cos f x x =， ③1()f x x =， ④1()lg 1x f x x-=+，则输出的函数是 ( ) A.()sin f x x = B.()cos f x x = C.1()f x x =D.1()lg 1x f x x-=+ 5.以下判断正确的是 ( )A.函数()y f x =为R 上可导函数，则()0f x '=是0x 为函数()f x 极值点的充要条件B.命题“存在2,10x R x x ∈+-<”的否定是“任意2,10x R x x ∈+->” C.“()2k k Z πϕπ=+∈”是“函数()sin()f x x ωϕ=+是偶函数”的充要条OBA件D.命题“在ABC ∆中，若,sin sin A B A B >>则”的逆命题为假命题6.一个长方体被一个平面截去一部分后，所剩几何体的三视图如图所示(单位：cm)， 则该几何体的体积为A.120 cm 3B.100 cm 3C.80 cm 3D.60 cm 37.若数列{}n a 的通项公式为221n n a n =+-，则数列{}n a 的前n 项和为 （ ） A.221nn +- B.1221n n ++- C.1222n n ++- D.22n n +-8.已知m ，n 是两条不同直线，α，β是两个不同平面，则下列命题正确的是（ ） A ．若α，β垂直于同一平面，则α与β平行 B ．若m ，n 平行于同一平面，则m 与n 平行C ．若α，β不平行，则在α内不存在与β平行的直线D ．若m ，n 不平行，则m 与n 不可能垂直于同一平面 9.函数sin(2),()y x ϕπϕπ=+-≤<的图象向右平移4π个单位后，与函数sin(2)3y x π=+ 的图象重合，则ϕ的值为 ( ) A. 56π-B. 56πC. 6π D. 6π- 10.如图所示,两个不共线向量,OA OB 的夹角为q ，,M N 分别为,OA OB 的中点,点C 在直线MN 上,且(,)OC xOA yOB x y R =+∈,则22x y +的最小值为（ ）A.4B.18C.2D.1211.在ABC ∆中，三个内角,,A B C 所对的边为,,a b c，若ABC S ∆=6a b +=，cos cos 2cos a B b AC c+=，则c =（ ）A ．．．12.已知函数f (x )＝x (ln x －ax )有两个极值点，则实数a 的取值范围是 ( ) A ．(,0)-∞ B ．1(0,)2C ．(0,1)D ．(0,)+∞ 二、填空题：本大题共4小题，每小题5分，共20分.13. 在等差数列{}n a 中，35710133()2()24a a a a a ++++=，则此数列前13项的和是 。

文科数学试卷一、选择题（本大题共10小题，每小题5分，共50分，每题只有一项是符合要求的）1．已知P 为椭圆192522=+y x 上一点, 12,F F 为椭圆的两个焦点，且13PF =,则2PF = ( )A. 2B. 5C. 7D. 82．在ABC ∆中，::1:2:3A B C =，则::a b c 等于 （ ） A ．1:2:3 B．2 C ．3:2:1 D．3．设n S 是等差数列{}n a 的前n 项和，已知23a =，611a =，则7S = （ ） A ．13 B ．35 C ．49 D ．634．如图，设,A B 两点在河的两岸，一测量者在A 的同侧，在所在的河岸边选定一点C ， 测出AC 的距离是50m ，∠ACB=45，∠CAB=105， 就可以计算出,A B 两点的距离为 （ ） A． B．C． D．2m 5．若抛物线的准线方程为x ＝－7，则抛物线的标准方程为 ( )A ．x 2＝－28yB ．x 2＝28yC ．y 2＝－28xD ．y 2＝28x 6．“n m =”是“方程122=+ny mx 表示圆”的 ( ) A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 7. 如右图所示为y =f ′(x )①f (x )在(－∞, 1)上是增函数； ②x ＝－1是f (x )的极小值点；③f (x )在(2, 4)上是减函数，在(－1, 2)上是增函数； ④x ＝2是f (x )的极小值点A ．①②③ B．①③④ C．③④ D．②③8．已知,x y 满足条件5003x y x y x -+≥⎧⎪+≥⎨⎪≤⎩，则23x yz +=的最小值为 （ ）A ．0B ．1C ．271 9．设等比数列{a n }的前n 项和为S n ，若S 2＝3，S 4＝15，则S 6＝ ( )A ．31B ．32C ．63D ．64 10．若221xy+=，则x y +的取值范围是 （ ）A ．[0,2]B ．[2,0]-C ．[)2,-+∞D ．(],2-∞- 二、填空题（本大题共5小题，每小题5分，共25分）11．等比数列{a n }的各项均为正数，且a 1a 5＝4，则log 2a 1＋log 2a 2＋log 2a 3＋log 2a 4＋log 2a 5＝ 。

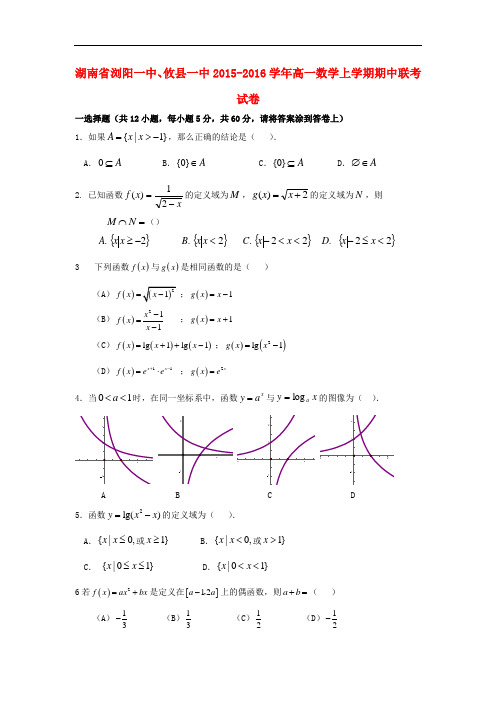
7.下列函数中，既在定义域上是增函数且图象又关于原点对称的是（ ） A.x y 2-= B.2lg 11y x ⎛⎫=- ⎪+⎝⎭C.x y 2=D.x x y -22+= 8函数x x x f ++=12)( 的值域是 （ ） A.[0,)+∞ B.1[,)2-+∞C.[0,)+∞D.[1,)+∞ 9．函数)32(log )(221--=x x x f 的单调递减区间为( )．A ． )1,(-∞B ． ),1(+∞C ． )1,(--∞D ．),3(+∞ 10．方程lg 30x x +-=的实根为0x ，则0x 位于区间（ ）内A ．),3(+∞B ．(2,3)C ．(1,2)D ．(0,1)11.若0.52a =，1.23.0=b ，5log 21=c ，5log 31=d 则（ ）A ．d c a b >>>B ．c d a b >>>C ．c d b a >>>D ．d c b a >>>12设函数()f x 定义在实数集上，且函数y=f(x+1)是偶函数，当1≥x 时，()12xf x ⎛⎫= ⎪⎝⎭，则有（ ）（A ）()11232f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭（B ）()11223f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭（C ）()11223f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭（D ）)21()31()2(f f f <<二填空题（共4小题，每小题5分，共20分，请将答案写到答卷上） 13.设集合{}3,1=A ，{}2,a a B =，{}1=B A I ，则实数=a _____.14．函数()log (23)1a f x x =-+的图像恒过定点P ，则点P 的坐标是 . 15．已知函数()2log ,0,3,0x x x f x x >⎧=⎨≤⎩则18f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦ ．16已知函数(31)4,1()log ,1a a x a x f x xx -+<⎧=⎨≥⎩0)()(R ,212121<--∈x x x f x f x x 都有对任意，那么a 的取值范围是 ；三解答题（共6小题） 17. (本小题满分10分)计算:（1()()411320.0080.25---⨯；（2）21log 31324lg 22493+--2log 9log 32⨯18. (本小题满分12分) 已知}0)3)((|{≤---=a x a x x A ，}016|{>-+=x x x B ． （1）化简集合A 、B ；（2）若A B =∅I ，求a 的取值范围； （3）若A B B =U ，求a 的取值范围．19已知二次函数()f x 满足0)1(=f ,且(1)()4 3.f x f x x +-=+ （1）求()f x 的解析式，（2）若()f x 在区间[,1]a a +上单调，求实数a 的取值范围.20．（本小题满分12分）如图，有一块矩形空地ABCD ，要在这块空地上开辟一个内接四边形EFGH 为绿地，使其四个顶点分别落在矩形的四条边上. 已知AB =a （a >2），BC =2，且AE =AH =CF =CG ，设AE =x ，绿地EFGH 面积为y .（1）写出y 关于x 的函数解析式，并求出它的定义域； （2）当AE 为何值时，绿地面积y 最大？并求出最大值。

湖南省浏阳市三校2018届高三数学上学期期中联考试题文编辑整理：尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（湖南省浏阳市三校２01８届高三数学上学期期中联考试题文)的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为湖南省浏阳市三校２0１8届高三数学上学期期中联考试题文的全部内容。

湖南省浏阳市三校２018届高三数学上学期期中联考试题 文考试时间:１50分钟；学校：__＿___＿__＿_姓名：＿__________班级：＿＿＿_＿___＿__考号:____＿______注意事项：1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上.ﻫﻫ第1卷评卷人得分一、选择题（本大题12小题，每小题5分,共6０分)1、函数最小值是( ）A 。

B. 1-2C 。

12 D.２、下列函数中,既是偶函数又在0+∞（，）上单调递增的是( )Ａ。

B 。

y=cos ｘ C. 21y x =D 。

3、下列结论错误的是( ） A 。

命题“若,则＂的逆否命题是“若,则”B.若命题，则C 。

若为真命题，则,均为真命题ﻫ D.“”是“”的充分不必要条件４、已知数列中,,则等于( )A 。

Ｂ。

Ｃ． D 。

5、定义在上的函数对任意两个不相等的实数,，总有，则必有( ）ﻫA ．函数先增后减 B 。

函数先减后增ﻫ C.函数在上是增函数 D 。

函数在上是减函数6、一质点沿直线运动,如果由始点起经过称后的位移为3231322s t t t =-+，那么速度为零的时刻是（ ) A 。

Ｂ．末 C ．末 D ．末和末７、在A ＢＣ中,若，则这个三角形一定是( ）A 。

湖南省浏阳一中、攸县一中2024-2025学年高三校内模拟考试自选模块试卷考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、单项选择题：本题共6小题，每小题4分，共24分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、如图所示为静止的原子核在匀强磁场中发生衰变后做匀速圆周运动的轨迹，衰变后两带电粒子a、b的半径之比为45∶1，两带电粒子a、b的动能之比为117：2，下列说法正确的是（）A．此衰变为β衰变B．大圆为β粒子的运动轨迹C．小圆为α粒子的运动轨迹D．两带电粒子a、b的周期之比为10∶132、如图所示，空间P点离地面足够高，从P点以很小的速度向右水平抛出一个小球，小球能打在竖直的墙壁上，若不断增大小球从P点向右水平抛出的初速度，则小球打在竖直墙壁上的速度大小A．一定不断增大B．一定不断减小C．可能先增大后减小D．可能先减小后增大3、如图所示，A，B质量均为m，叠放在轻质弹簧上（弹簧上端与B不连接，弹簧下端固定于地面上）保持静止，现对A施加一竖直向下、大小为F（F＞2mg）的力，将弹簧再压缩一段距离（弹簧始终处于弹性限度内）而处于静止状态，若突然撤去力F，设两物体向上运动过程中A、B间的相互作用力大小为F N，则关于F N的说法正确的是（重力加速度为g）（）A．刚撤去外力F时，B．弹簧弹力等于F时，C．两物体A、B的速度最大时，F N=2mgD．弹簧恢复原长时，F N=mg4、帆船运动中，运动员可以调节帆面与船前进方向的夹角，使船能借助风获得前进的动力．下列图中能使帆船获得前进动力的是A．B．C．D．5、手机A的号码为138****1111，手机B的号码为130****2222.当手机A拨打手机B时，能听见B发出响声并且看见B上来电显示A的号码为138****1111.若将手机A置于透明真空罩中，再用手机B拨打手机A，则A．能听见A发出响声，但看不到A上显示B的号码B．能听见A发出响声，也能看到A上显示B的号码130****2222C．既不能听见A发出响声，也看不到A上显示B的号码D．不能听见A发出响声，但能看到A上显示B的号码130****22226、两辆汽车a、b在两条平行的直道上行驶。

2016年下学期浏阳一中、攸县一中高三文科数学学联考试题一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{}2430A x x x =-+<，{}2|,R B y y x x ==∈，则B A ⋂= A ．∅ B ．[)()+∞⋃,31,0 C ．（0,3) D ．(1,3) 2．若(1i)i z =+（i 为虚数单位），则Z 的虚部是( )A ．1B ．1-C ．iD ．i -3．设等差数列{}n a 的前n 项和为,n S 2a 、4a 是方程220x x --=的两个根，则5S =A ．52-B ．5-C ．5D ．524．已知命题:0p a b >>，命题:q a b a b +<+，则命题p 是q 的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件 5．三个数43log 、9.01.1log 、43.0的大小顺序是…………………………………………（ ）A 、43log >9.01.1log >43.0 B 、43log >43.0>9.01.1log C 、9.01.1log >43log >43.0 D 、43.0>43log >9.01.1log6.在ABC ∆中，o o B A c 45,75,3===，则ABC ∆的外接圆面积为（ ） A ．4πB ．πC ．π2D ．π4 7. 若函数y ＝xa （a ＞0，且a ≠1）的值域为{y ｜0＜y ≤1}，则函数y ＝log a x 的图像大致是（ ）8． 已知函数的定义域为)(x f ),2[+∞-，且1)2()4(=-=f f ，)()(x f x f 为'的导函数，函数)(x f y '=的图象如图所示. 则平面区域⎪⎩⎪⎨⎧<+≥≥1)2(00b a f b a 所围成的面积是( )A ．8B ．5C ．4D ．29．已知()x f 在R 上是奇函数，且满足()()x f x f -=+5，当()5,0∈x 时，()x x x f -=2，则()=2016f （ ） A ．-12 B.-16 C.-20 D.0 10．定义运算：,,a a ba b b a b≤⎧*=⎨>⎩．例如121*=，则函数()sin cos f x x x =*的值域为（ ）A ．22⎡-⎢⎣⎦B ．[]1,1-C ．2⎤⎢⎥⎣⎦D ．1,2⎡-⎢⎣⎦ 11．已知数列{}n a ，若点*(,)()n n a n N ∈在经过点（5，3）的定直线l 上，则数列{}n a 的前9项和9S = ( )A ．9B ．10C ．18D ．2712．设函数()''y f x =是()'y f x =的导数.某同学经过探究发现，任意一个三次函数()()320f x ax bx cx d a =+++≠都有对称中心()()00,x f x ，其中0x 满足()0''0f x =.已知函数()3211533212f x x x x =-+-，则1232016...2017201720172017f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭（ ） A ．2013 B ．2014 C ．2015 D ．2016 二、填空题： 本题共4小题，每小题5分，共20分． 13．函数x y 5.0log =的定义域为___________.14．设等比数列{}n a 满足,1031=+a a ,542=+a a 则n a a a 21的最大值为 .15.在矩形ABCD 中，=⋅=⋅=∠30CAB 0， .16．已知偶函数)(x f 满足()(2)0f x f x -+=，且当]1,0[∈x 时，xe x xf ⋅=)(，若在区间]3,1[-内，函数k kx x f x g 2)()(--=有且仅有3个零点，则实数k 的取值范围是 ．三、解答题：本题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤． 17.（10分）已知函数,cos 2)322cos()(2x x x f ++=π（1）求函数)(x f 的最小正周期和单调减区间； （2）将函数)(x f 图象向右平移3π个单位长度后得到函数)(x g 的图象，求函数)(x g 在区间[0,2π]上的最小值。

攸县一中、浏阳一中2015年下学期高一期中考试联考试卷数学试卷命题、审题：浏阳一中高一数学组一选择题（共12小题，每小题5分，共60分，请将答案涂到答卷上）1．如果，那么正确的结论是（）．A．B．C．D．2. 已知函数的定义域为，的定义域为，则（）3下列函数与是相同函数的是（）（A）；（B ） ；（C ）()()()lg 1lg 1f x x x =++- ；（D ） ；）．A5．函数）．A．或B．或C．D．6若是定义在上的偶函数，则（）（A）（B）（C）（D）7.下列函数中，既在定义域上是增函数且图象又关于原点对称的是（）A. B. C.D.8函数的值域是（）A. B.C.D.9．函数)32(log )(221--=x x x f 的单调递减区间为()．A ．B ．C ．D．10．方程的实根为，则位于区间（）内A． B．C．D．11.若，，，则（） A．B．C． D．12设函数定义在实数集上，且函数y=f(x+1)是偶函数，当时，，则有（）（A）（B）（C）（D）二填空题（共4小题，每小题5分，共20分，请将答案写到答卷上）13.设集合，，，则实数_____.14．函数()log (23)1a f x x =-+的图像恒过定点，则点的坐标是 .15．已知函数()2log ,0,3,0x x x f x x >⎧=⎨≤⎩则．16已知函数(31)4,()log ,1a a x a x f x xx -+<⎧=⎨≥⎩0)()(R ,212121<--∈x x x f x f x x 都有对任意，那么的取值范围是 ；三解答题（共6小题） 17. (本小题满分10分)计算:（1()()411320.0080.25---⨯；（2）21log 31324lg 22493+--18. (本小题满分12分) 已知}0)3)((|{≤---=a x a x x A ，．（1）化简集合A 、B ；（2）若，求的取值范围；（3）若，求的取值范围．19已知二次函数满足,且(1)()4 3.f x f x x +-=+（1）求的解析式，（2）若在区间上单调，求实数的取值范围.20．（本小题满分12分）如图，有一块矩形空地ABCD ，要在这块空地上开辟一个内接四边形EFGH 为绿地，使其四个顶点分别落在矩形的四条边上. 已知AB =a （a >2），BC =2，且AE =AH =CF =CG ，设AE =x ，绿地EFGH 面积为y .ABC D EF GH（1）写出y关于x的函数解析式，并求出它的定义域；（2）当AE为何值时，绿地面积y最大？并求出最大值。