棱锥台的表面积和体积的计算公式

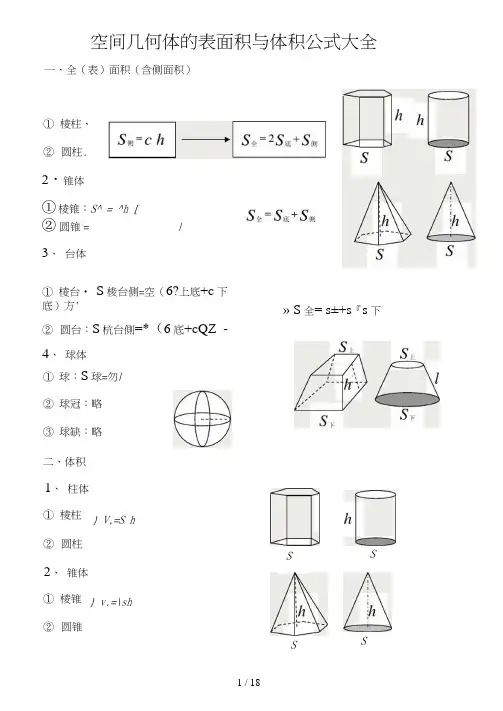
空间几何体的表面积与体积公式大全一、全（表）面积（含侧面积）①棱柱、②圆柱.2・锥体①棱锥：S^ = ^h [②圆锥:= /3、台体①棱台• S梭台侧=空（6?上底+c下底）方'» S全= s±+s『s下②圆台：S杭台側=*（6底+cQZ -4、球体①球：S球=勿/②球冠：略③球缺：略二、体积1、柱体①棱柱} V,=S h②圆柱S S 2、锥体①棱锥} v.=\sh②圆锥S S3、 台体V 台肓//（S 匕+ JS 上S F + S 下）台=齐方（厂上+Jr 上厂下+厂下） 4、 球体①球：V 球② 球冠：略VyT/③ 球缺：略说明：棱锥、棱台计算侧面积时使用侧面的斜高力计算；而圆锥、圆台的 侧面积计算时使用母线/计算。

三、拓展提高1、 祖眶原理：（祖璀：祖冲之的儿子）夹在两个平行平面间的两个几何体，如果它们在任意高度上的平行截面面积都相等，那么这两个几何体的体积相等。

最早推导出球体体积的祖冲之父子便是运用这个原理实现的。

2、 阿基米德原理：（圆柱容球）圆柱容球原理：在一个高和底面直径都是2厂的圆柱形容器内装一个最大 的球体，则该球体的全面积等于圆柱的侧面积，体积等于圆柱体积的？。

①棱台 ②圆台丿分析：圆柱体积：V H1 = s h =（^r）x2r = 2^/圆柱侧面积：S叭削= c/z = （2岔）X2广=4兀/2 彳4 彳因lit :球体体积：|/厅=—x2/r^ =_龙厂球体表面积：S球=4兀厂通过上述分析，我们可以得到一个很重要的关系（如图）即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和3、台体体积公式公式：几冷〃（S上+、恳瓦+ S』证明：如图过台体的上下两底面中心连线的纵切面为梯形ABCD。

延长两侧棱相交于一点P 0设台体上底面积为Si，下底面积为S下高为// °易知：\PDCs 型AB，设卩£ =人，则Pf+h由相似三角形的性质得：孚=袋AB PF即：（相似比等于面积比的算术平方根）、用hi整理得：人=尺刃又因为台体的体积二大锥体体积一小锥体体积u台=§s下（九+力r s上人人（S下-S上）+§s下方即：（、瓦+丫瓦）+扣下力=|/z $ + 应7+S卜）4、球体体积公式推导分析：将半球平行分成相同高度的若干层（兀层），〃越大，每一层越近似于圆柱'"T -HZ）时»每一层都可以看作是一个圆柱。

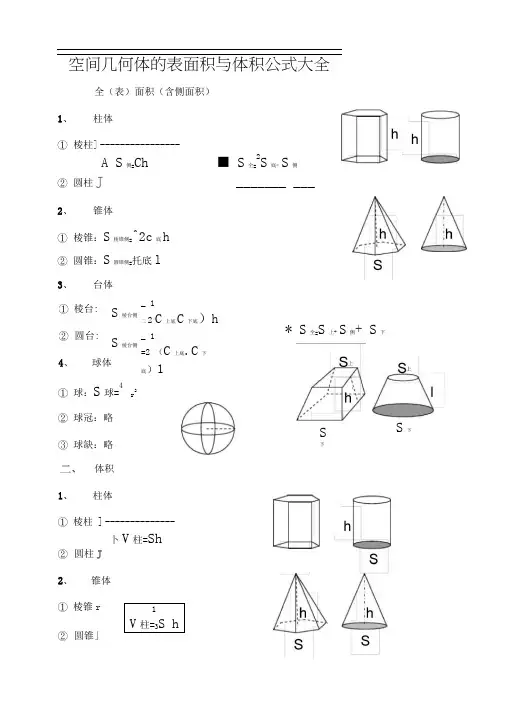
空间几何体的表面积与体积公式大全全（表）面积（含侧面积）1、柱体①棱柱]----------------A S侧=Ch ■ S全=2S底* S侧②圆柱J _______ ___2、锥体①棱锥：S棱锥侧=^2c底h②圆锥：S圆锥侧=托底l3、台体①棱台:②圆台:S棱台侧S棱台侧_ 1二2（C上底C下底）h_ 1=2 （C上底.C下底）1* S全=S上+ S侧+ S下4、球体①球：S球=4r2②球冠：略③球缺：略S下S下体积1、柱体①棱柱]--------------卜V柱=Sh②圆柱J2、锥体①棱锥r②圆锥」1V柱=3S h3、台体1①棱台］V台=gh （S上NS上S^ +S下）②圆台J V圆台=3兀h （r上+Q r上r下+ r下）4、球体①球：V球=4二r'②球冠：略③球缺：略说明：棱锥、棱台计算侧面积时使用侧面的斜高h计算；而圆锥、圆台的侧面积计算时使用母线I计算。

三、拓展提高1、祖暅原理：（祖暅：祖冲之的儿子）夹在两个平行平面间的两个几何体，如果它们在任意高度上的平行截面面积都相等，那么这两个几何体的体积相等。

最早推导出球体体积的祖冲之父子便是运用这个原理实现的2、阿基米德原理：（圆柱容球）圆柱容球原理：在一个高和底面直径都是2r的圆柱形容器内装一个最大的球体，则该球体的全面积等于圆柱的侧面积，体积等于圆柱体积的-。

3分析：圆柱体积：V圆柱=Sh =（二「2）2r=2^r'圆柱侧面积：S圆柱侧=C h =（2 r） 2r = 4二「因此：球体体积：V球=2 2二J=4二r33 3球体表面积：S球=4 r2即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和3、台体体积公式公式：V台=1h （S上+ S下）证明：如图过台体的上下两底面中心连线的纵切面为梯形ABCD 延长两侧棱相交于一点P设台体上底面积为S上,下底面积为S下P 高为h。

易知：PDC s .>PAB ,设PE = h i，则PF =h i h由相似三角形的性质得:CD PEAB PFA整理得：h 1 ： =S上hPS 下-VS上又因为台体的体积=大锥体体积一小锥体体积1 11 1 二V台=3S 下(h 1h K3S 上h^3h 1(S下一S上) 下h代入：h= i S 上芬得: V台=3胪L(S下—S"3S 下hJS下3*SrS31 ___ I ------ ------ 1即: V 台=3 S上h (S下S上)3S下人二 V 台=3h （S 上S 上S 下S下）球体体积公式推导即：ShiS 下-h lh （相似比等于面积比的算术平方根）1 ______________=3h (S上S 上S 下S下)4、分析：将半球平行分成相同高度的若干层（ n 层），n 越大，每一层越近似于圆柱，n “ •「时，每一层都可以看作是个圆柱。

棱柱棱锥棱台的表面积和体积教案一、引言在几何学中，棱柱、棱锥和棱台是常见的三维几何体。

它们有着不同的特点和性质，但是计算其表面积和体积的方法却有一定的相似之处。

本教案将针对棱柱、棱锥和棱台的表面积和体积进行详细讲解，并提供相应的计算公式和实例。

二、棱柱1. 定义和性质棱柱是一个底面是一个多边形的立体，且顶部和底部平行，并由与底面对应的一组边相连接而成。

棱柱的侧面全部是矩形，而顶部和底部是多边形。

2. 表面积的计算棱柱的表面积由底面积和侧面积两部分组成。

计算公式如下：表面积 = 底面积 + 侧面积底面积的计算取决于底面的形状，可以是正多边形或其他形状。

假设底面的周长为P，高度为h，则底面积可以表示为：底面积 = P * h/2侧面积的计算有两种情况： - 若底面是正多边形，侧面积可以通过计算正多边形周长P和高度h的乘积得到：侧面积 = P * h - 若底面是其他形状，侧面积需要通过分解为多个矩形，计算每个矩形的面积，然后求和得到。

3. 体积的计算棱柱的体积可以通过计算底面积和高度的乘积得到，即：体积 = 底面积 * 高度三、棱锥1. 定义和性质棱锥是一个底面是一个多边形的立体，且顶部是一个顶点。

棱锥的侧面全部是三角形，而底面是多边形。

2. 表面积的计算棱锥的表面积由底面积和侧面积两部分组成。

计算公式如下：表面积 = 底面积 + 侧面积底面积的计算方法与棱柱相同。

侧面积的计算可以通过计算棱锥的侧面积和底面积之和得到，即：侧面积 = 底面积 + 棱锥侧面积棱锥侧面积的计算可以通过计算底面的周长和斜高的乘积得到，斜高可以通过勾股定理求得。

3. 体积的计算棱锥的体积可以通过计算底面积和高度的乘积再除以3得到，即：体积 = 底面积* 高度 / 3四、棱台1. 定义和性质棱台是一个上底面和下底面是两个平行的多边形的立体。

棱台的侧面全部是梯形，而上底面和下底面是多边形。

2. 表面积的计算棱台的表面积由上底面积、下底面积和侧面积三部分组成。

7．2 棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积学习目标 1.掌握柱体、锥体、台体的体积计算公式，会利用它们求有关几何体的体积.2.掌握求几何体体积的基本技巧．知识点一 柱、锥、台体的体积公式知识点二 柱体、锥体、台体的体积公式之间的关系V ＝ShV ＝13(S ′＋S ′S ＋S )hV ＝13Sh .1．锥体的体积等于底面面积与高之积．( × ) 2．台体的体积可转化为两个锥体的体积之差．( √ )类型一 多面体的体积例1 如图，四边形ABCD 为正方形，QA ⊥平面ABCD ，PD ∥QA ，QA ＝AB ＝12PD .(1)证明：PQ ⊥平面DCQ ；(2)求棱锥Q －ABCD 的体积与棱锥P －DCQ 的体积的比值． (1)证明 由题知四边形PDAQ 为直角梯形． 因为QA ⊥平面ABCD ，QA 平面PDAQ ， 所以平面PDAQ ⊥平面ABCD ，交线为AD . 又四边形ABCD 为正方形，DC ⊥AD ， 所以DC ⊥平面PDAQ ，可得PQ ⊥DC . 在直角梯形PDAQ 中可得DQ ＝PQ ＝22PD ， 则PQ ⊥QD .又DC ∩QD ＝D ，DC ，QD 平面DCQ ， 所以PQ ⊥平面DCQ .(2)解 设AB ＝a .由题设知AQ 为棱锥Q －ABCD 的高， 所以棱锥Q －ABCD 的体积V 1＝13a 3.由(1)知PQ 为棱锥P －DCQ 的高． 而PQ ＝2a ，△DCQ 的面积为22a 2， 所以棱锥P －DCQ 的体积V 2＝13a 3.故棱锥Q －ABCD 的体积与棱锥P －DCQ 的体积的比值为1. 反思与感悟 求几何体体积的四种常用方法 (1)公式法：规则几何体直接代入公式求解．(2)等积法：如四面体的任何一个面都可以作为底面，只需选用底面积和高都易求的形式即可． (3)补体法：将几何体补成易求解的几何体，如棱锥补成棱柱、三棱柱补成四棱柱等． (4)分割法：将几何体分割成易求解的几部分，分别求体积．跟踪训练1 如图，在三棱柱111ABC A B C －中，若E ，F 分别为AB ，AC 的中点，平面11EB C F 将三棱柱分成体积为l 2V V ，的两部分，那么12:V V ＝________.答案 7∶5解析 设三棱柱的高为h ，底面的面积为S ，体积为V ，则V ＝V 1＋V 2＝Sh . 因为E ，F 分别为AB ，AC 的中点，所以AEFS ＝14S ， 1V ＝13h ⎝⎛⎭⎫S ＋14S ＋S ·S 4＝712Sh ， 2V ＝Sh －1V ＝512Sh ，故12:7:5V V ＝.类型二 旋转体的体积例2 体积为52 cm 3的圆台，一个底面面积是另一个底面面积的9倍，求截得这个圆台的圆锥的体积．解 由底面面积之比为1∶9知，体积之比为1∶27. 截得的小圆锥与圆台体积比为1∶26， ∴小圆锥的体积为2 cm 3， 故原来圆锥的体积为54 cm 3.反思与感悟 要充分利用旋转体的轴截面，将已知条件尽量归结到轴截面中求解，分析题中给出的数据，列出关系式后求出有关的量，再根据几何体的体积公式进行运算、解答． (1)求台体的体积，其关键在于求高，在圆台中，一般把高放在等腰梯形中求解．(2)“还台为锥”是求解台体的体积问题的重要思想，作出截面图，将空间问题平面化，是解决此类问题的关键．跟踪训练2 设圆台的高为3，如图，在轴截面中母线AA 1与底面直径AB 的夹角为60°，轴截面中的一条对角线垂直于腰，则圆台的体积为________．考点 题点答案 21π解析 设上，下底面半径，母线长分别为r ，R ，l .作A 1D ⊥AB 于点D ，则A 1D ＝3，∠A 1AB ＝60°， 又∠BA 1A ＝90°， ∴∠BA 1D ＝60°， ∴AD ＝A 1Dtan 60°＝3， ∴R －r ＝ 3.BD ＝A 1D ·tan 60°＝33，∴R ＋r ＝3 3.∴ R ＝23，r ＝3，而h ＝3.∴V 圆台＝13πh (R 2＋Rr ＋r 2)＝13π×3×[(23)2＋23×3＋(3)2]＝21π.∴圆台的体积为21π. 类型三 几何体体积的求法 命题角度1 等体积法例3 如图，已知ABCD －A 1B 1C 1D 1是棱长为a 的正方体，E 为AA 1的中点，F 为CC 1上一点，求三棱锥A 1－D 1EF 的体积．考点 柱体、锥体、台体的体积 题点 锥体的体积解 1111A D EF F A D E V V －－＝，锥锥三棱三棱由1121111124A D E S EA A D a ∆⋅＝＝， 又三棱锥F －A 1D 1E 的高为CD ＝a ，11231113412F A D E V a a a ∴⨯⨯－＝＝，锥三棱 1131.12A D EF V a ∴－＝三棱锥反思与感悟 (1)三棱锥的每一个面都可当作底面来处理． (2)利用等体积法可求点到面的距离．跟踪训练3 如图所示，正方体ABCD －A 1B 1C 1D 1的棱长为1，在三棱锥A 1－ABD 中，求A 到平面A 1BD 的距离d .考点 题点解 在三棱锥A 1－ABD 中，AA 1是三棱锥A 1－ABD 的高，AB ＝AD ＝AA 1＝1，A 1B ＝BD ＝A 1D ＝ 2.∵13×12×12×1＝13×12×2×32×2×d ， ∴d ＝33. 命题角度2 割补法例4 如图，在多面体ABCDEF 中，已知面ABCD 是边长为4的正方形，EF ∥AB ，EF ＝2，EF 与平面AC 的距离为3，求该多面体的体积．考点 题点解 如图，连接EB ，EC ，AC .四棱锥E －ABCD 的体积V E －ABCD ＝13×42×3＝16.因为AB ＝2EF ，EF ∥AB ，所以S △EAB ＝2S △BEF .所以V F －EBC ＝V C －EFB ＝12V C －ABE ＝12V E －ABC＝12×12V E －ABCD ＝4. 所以该多面体的体积V ＝V E －ABCD ＋V F －EBC ＝16＋4＝20.反思与感悟 通过“割补法”解决空间几何体的体积问题，需要思路灵活，有充分的空间想象力，什么时候“割”，什么时候“补”，“割”时割成几个图形，割成什么图形，“补”时补上什么图形，都需要灵活的选择．跟踪训练4 如图所示，一个底面半径为2的圆柱被一平面所截，截得的几何体的最短和最长母线长分别为2和3，求该几何体的体积．考点 题点解 用一个完全相同的几何体把题中几何体补成一个圆柱，如图所示，则圆柱的体积为π×22×5＝20π，故所求几何体的体积为10π.1.已知高为3的棱柱ABC —A 1B 1C 1的底面是边长为1的正三角形(如图)，则三棱锥B 1—ABC 的体积为( )A.14B.12C.36D.34考点 柱体、锥体、台体的体积 题点 锥体的体积答案 D解析 V ＝13Sh ＝13×34×3＝34.2．圆锥的轴截面是等腰直角三角形，侧面积是162π，则圆锥的体积是( ) A.128π3 B.64π3 C ．64π D ．1282π考点 柱体、锥体、台体的体积 题点 锥体的体积 答案 B解析 设圆锥的底面半径为r ，母线长为l ， 由题意知2r ＝l 2＋l 2，即l ＝2r ，∴S 侧＝πrl ＝2πr 2＝162π， 解得r ＝4.∴l ＝42，圆锥的高h ＝l 2－r 2＝4，∴圆锥的体积为V ＝13Sh ＝13π×42×4＝64π3.3．棱台的上、下底面面积分别是2,4，高为3，则该棱台的体积是( ) A ．18＋6 2 B ．6＋2 2 C ．24 D ．18考点 题点 答案 B解析 V ＝13(2＋4＋2×4)×3＝6＋2 2.4．已知某圆台的上、下底面面积分别是π，4π，侧面积是6π，则这个圆台的体积是________． 考点题点 台体的体积 答案73π3解析 设圆台的上、下底面半径分别为r 和R ，母线长为l ，高为h ，则S 上＝πr 2＝π，S 下＝πR 2＝4π.∴r ＝1，R ＝2，S 侧＝π(r ＋R )l ＝6π.∴l ＝2，∴h ＝3，∴V ＝13π(12＋22＋1×2)×3＝73π3.5．如图是一个底面直径为20 cm 的装有一部分水的圆柱形玻璃杯，水中放着一个底面直径为6 cm ，高为20 cm 的圆锥形铅锤，当铅锤从水中取出后，杯里的水将下降__________cm.考点 题点 答案 0.6解析 将铅锤取出后，水面下降部分实际是圆锥的体积． 设水面下降的高度为x cm ，则π×⎝⎛⎭⎫2022x ＝13π×⎝⎛⎭⎫622×20， 得x ＝0.6 cm.1．柱体、锥体、台体的体积之间的内在关系为V 柱体＝Sh ←―――S ′＝S V 台体＝13h (S ＋SS ′＋S ′)――→S ′＝0V 锥体＝13Sh .2．在三棱锥A －BCD 中，若求点A 到平面BCD 的距离h ，可以先求V A －BCD ，h ＝3V S △BCD.这种方法就是用等体积法求点到平面的距离，其中V 一般用换顶点法求解，即V A －BCD ＝V B －ACD ＝V C －ABD ＝V D －ABC ，求解的原则是V 易求，且△BCD 的面积易求．3．求几何体的体积，要注意分割与补形．将不规则的几何体通过分割或补形将其转化为规则的几何体求解．一、选择题1.如图，ABC －A ′B ′C ′是体积为1的棱柱，则四棱锥C －AA ′B ′B 的体积是( )A.13B.12C.23D.34考点 题点 答案 C解析 ∵V C －A ′B ′C ′＝13V ABC －A ′B ′C ′，∴V C －AA ′B ′B ＝23V ABC －A ′B ′C ′＝23.2.如图，已知正三棱锥S －ABC ，D ，E 分别为底面边AB ，AC 的中点，则四棱锥S －BCED 与三棱锥S －ABC 的体积之比为( )A ．1∶2B ．2∶3C ．3∶4D ．4∶3答案 C解析 两锥体高相等，因此V 四棱锥S －BCED ∶V 三棱锥S －ABC ＝S 四边形BCED ∶S △ABC ＝3∶4. 3．已知圆锥的母线长为8，底面圆的周长为6π，则它的体积是( ) A ．955π B ．955 C ．355π D ．355 考点 题点 答案 C解析 设圆锥的底面圆的半径为r ，高为h ，则2πr ＝6π，∴r ＝3. ∴h ＝64－32＝55，∴V ＝13π·r 2·h ＝355π.4.如图，在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2，将梯形ABCD 绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.53πB.43πC.23π D ．2π 考点 组合几何体的表面积与体积题点 柱、锥、台、球切割的几何体的表面积与体积 答案 A解析 由题意，旋转而成的几何体是圆柱，挖去一个圆锥(如图)，该几何体的体积为π×12×2－13×π×12×1＝53π.5．若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的母线长为( ) A ．2 B ．2 2 C. 2 D. 3 考点 题点 答案 A解析 如图所示，设等边三角形ABC 为圆锥的轴截面，由题意知圆锥的母线长即为△ABC 的边长，且S △ABC ＝34AB 2，∴3＝34AB 2，∴AB ＝2.6．如图所示，正方体ABCD －A 1B 1C 1D 1的棱长为1，则三棱锥D 1－ACD 的体积是( )A.16B.13C.12D ．1答案 A 解析 三棱锥D 1－ADC 的体积V ＝13S △ADC ×D 1D ＝13×12×AD ×DC ×D 1D ＝13×12＝16. 7．将若干毫升水倒入底面半径为2 cm 的圆柱形器皿中，量得水面高度为6 cm ，若将这些水倒入轴截面是正三角形的倒圆锥形器皿中，则水面高度为( )A ．6 3 cmB ．6 cmC ．2318 cmD ．3312 cm 考点 柱体、锥体、台体的体积题点 锥体的体积答案 B解析 设圆锥中水的底面半径为r cm ，由题意知13πr 2×3r ＝π22×6， 得r ＝23，∴水面的高度是3×23＝6 cm.8．正三棱柱ABC －A 1B 1C 1的底面边长为2，侧棱长为3，D 为BC 的中点，则三棱锥A －B 1DC 1的体积为( )A ．1 B.32 C ．3 D.32考点题点答案 A解析 在正△ABC 中，D 为BC 中点，则有AD ＝32AB ＝3，11DB C S ＝12×2×3＝ 3. 又∵平面BB 1C 1C ⊥平面ABC ，平面BB 1C 1C ∩平面ABC ＝BC ，AD ⊥BC ，AD 平面ABC ，∴AD ⊥平面BB 1C 1C ，即AD 为三棱锥A －B 1DC 1底面上的高．∴1111DB C A B DC V S 三棱－＝锥·AD ＝13×3×3＝1. 二、填空题9．设甲、乙两个圆柱的底面积分别为S 1，S 2，体积分别为V 1，V 2.若它们的侧面积相等，且S 1S 2＝94，则V 1V 2的值是________． 考点题点答案 32解析 设两个圆柱的底面半径和高分别为r 1，r 2和h 1，h 2，由S 1S 2＝94，得πr 21πr 22＝94，则r 1r 2＝32. 由圆柱的侧面积相等，得2πr 1h 1＝2πr 2h 2，即r 1h 1＝r 2h 2，所以V 1V 2＝πr 21h 1πr 22h 2＝r 1r 2＝32. 10.如图，在△ABC 中，AB ＝8，BC ＝10，AC ＝6，DB ⊥平面ABC ，且AE ∥FC ∥BD ，BD ＝3，FC ＝4，AE ＝5.则此几何体的体积为________．考点题点答案 96解析 用“补形法”把原几何体补成一个直三棱柱，使AA ′＝BB ′＝CC ′＝8，所以V 几何体＝12V 三棱柱＝12×S △ABC ·AA ′＝12×24×8＝96.11.如图，在三棱柱A 1B 1C 1－ABC 中，已知D ，E ，F 分别为AB ，AC ，AA 1的中点，设三棱锥A －FED 的体积为V 1，三棱柱A 1B 1C 1－ABC 的体积为V 2，则V 1∶V 2的值为______．考点 柱体、锥体、台体的表面积与体积题点 其他求体积、表面积问题答案 124解析 设三棱柱的高为h ，∵F 是AA 1的中点，∴三棱锥F －ADE 的高为h 2， ∵D ，E 分别是AB ，AC 的中点，∴S △ADE ＝14S △ABC ， ∵V 1＝13S △ADE ·h 2，V 2＝S △ABC ·h ， ∴V 1V 2＝16S △ADE ·h S △ABC ·h ＝124. 三、解答题12．在四边形ABCD 中，A (0,0)，B (1,0)，C (2,1)，D (0,3)，绕y 轴旋转一周，求所得旋转体的体积．解 如图为所得旋转体，由一个圆锥和一个圆台组成．∵C (2,1)，D (0,3)，∴圆锥的底面半径r ＝2，高h ＝2.∴V 圆锥＝13πr 2h ＝13π×22×2 ＝83π.∵B (1,0)，C (2,1)， ∴圆台的两个底面半径R ＝2，R ′＝1，高h ′＝1.∴V 圆台＝13πh ′(R 2＋R ′2＋RR ′) ＝13π×1×(22＋12＋2×1)＝73π， ∴V ＝V 圆锥＋V 圆台＝5π.13.如图所示是一个边长为5＋2的正方形，剪去阴影部分得到圆锥的侧面和底面展开图，求该圆锥的体积．考点题点解 设圆锥的底面半径为r ，母线长为l ，高为h ，则依题意有14·2πl ＝2πr ， ∴l ＝4r .又∵AC ＝OC ＋OA ＝2r ＋r ＋l ＝(2＋5)r ，且AC ＝2×(2＋5)，∴(2＋5)r ＝(2＋5)×2，∴r ＝2，∴l ＝42，∴h ＝l 2－r 2＝30，∴V 圆锥＝13πr 2h ＝13π(2)2×30＝2303π.故该圆锥的体积为2303π. 四、探究与拓展14．若正三棱台A 1B 1C 1－ABC 的两底面边长分别为2,8，侧棱长等于6，则此三棱台的体积V ＝________.答案 42 2解析 如图，设D 1，D 分别为A 1B 1，AB 的中点，O 1，O 为上、下两底面的中心，则O 1O 为棱台的高h ，O 1C 1＝233，OC ＝833，作C 1H ⊥OC 于点H ，则C 1H ＝h ，且CH ＝23，故h ＝C 1H ＝36－12＝2 6. ∵111A B C S ＝3，S △ABC ＝163，∴V ＝(3＋43＋163)×263＝42 2. 15.在三棱台ABC －A 1B 1C 1中，AB ∶A 1B 1＝1∶2，则三棱锥A 1－ABC ，B －A 1B 1C ，C －A 1B 1C 1的体积之比是多少？考点题点解 设棱台的高为h ，S △ABC ＝S ，则1114.A B C S S ∆＝ ∴1A ABC V －＝13S △ABC ·h ＝13Sh ， 1111114·.3C ABC A B C V S h Sh ∆－＝＝又V 台＝13h (S ＋4S ＋2S )＝73Sh ， ∴11B A B C V －＝V 台－1111A ABC C ABC V V －－－＝73Sh －13Sh －43Sh ＝23Sh . ∴1A ABC V －∶11B A B C V －∶111C A B C V －＝1∶2∶4.。

棱锥棱柱的表面积体积以棱锥和棱柱的表面积和体积为标题，我们将分别介绍棱锥和棱柱以及它们的表面积和体积的计算方法。

一、棱锥的表面积和体积1. 棱锥的定义和特点棱锥是一种具有一个顶点和n个侧面的几何体。

其中，顶点连接着棱锥的底面的每个角。

棱锥的底面可以是任何形状，例如三角形、四边形等。

2. 棱锥的表面积棱锥的表面积等于其底面的面积加上所有侧面的面积之和。

假设棱锥的底面面积为B，侧面的面积为S，则棱锥的表面积为S = B + Ss，其中Ss为侧面的总面积。

3. 棱锥的体积棱锥的体积等于其底面的面积乘以其高度再除以3。

假设棱锥的底面面积为B，高度为h，则棱锥的体积为V = (B × h) / 3。

二、棱柱的表面积和体积1. 棱柱的定义和特点棱柱是一种具有两个平行底面和n个侧面的几何体。

其中，棱柱的侧面是由底面的每个点和对应点的直线段组成的。

2. 棱柱的表面积棱柱的表面积等于其两个底面的面积加上所有侧面的面积之和。

假设棱柱的底面面积为B，侧面的面积为S，则棱柱的表面积为S = 2B + Ss，其中Ss为侧面的总面积。

3. 棱柱的体积棱柱的体积等于其底面的面积乘以其高度。

假设棱柱的底面面积为B，高度为h，则棱柱的体积为V = B × h。

三、应用举例1. 棱锥的应用举例棱锥常见的应用包括建筑、工程和几何学等领域。

例如，在建筑中，棱锥形的屋顶可以提供更大的内部空间，同时增加建筑的美观度。

在几何学中，棱锥可以作为教学工具，用于教授三维几何的概念和计算方法。

2. 棱柱的应用举例棱柱也有许多实际应用。

在建筑中，棱柱形的柱子通常用于支撑建筑物的结构。

在工程中，棱柱形的管道可以用于输送液体或气体。

此外，棱柱还可以作为容器或储物箱使用。

总结：本文介绍了棱锥和棱柱的定义和特点，并分别介绍了它们的表面积和体积的计算方法。

棱锥的表面积等于底面的面积加上所有侧面的面积之和，体积等于底面的面积乘以高度再除以3。

推导公式棱柱与棱锥的体积与表面积计算在数学的几何学中，计算几何体的体积和表面积是常见的问题。

本文将讨论推导公式来计算棱柱和棱锥的体积和表面积。

一、棱柱的体积和表面积计算公式推导棱柱是由两个平行且相等的多边形底面和连接它们的矩形侧面组成。

假设底面为正n边形，边长为a，高为h。

下面推导出棱柱的体积和表面积计算公式。

1. 棱柱的体积计算公式我们可以将棱柱分解为多个矩形和两个底面。

每个矩形的面积为底面的边长乘以高h。

因为棱柱有n个这样的矩形，所以总体积V可以表示为：V = n * a * h2. 棱柱的表面积计算公式棱柱的表面积由两个底面和多个矩形的面积之和构成。

两个底面的面积相等，可以表示为n * a²，而每个矩形的面积为底面边长a乘以高h。

所以棱柱的表面积S可以表示为：S = n * a² + 2 * n * a * h二、棱锥的体积和表面积计算公式推导棱锥是由一个多边形底面和连接它们的三角形侧面组成。

假设底面为正n边形，边长为a，高为h。

下面推导出棱锥的体积和表面积计算公式。

1. 棱锥的体积计算公式与棱柱类似，我们可以将棱锥看作是多个三角形和一个底面的组合体。

每个三角形的面积可以表示为底面边长a乘以高h再除以2。

因为棱锥有n个这样的三角形，所以总体积V可以表示为：V = (n * a * h) / 32. 棱锥的表面积计算公式棱锥的表面积由底面和多个三角形的面积之和构成。

底面的面积为n * a²，而每个三角形的面积为底面边长a乘以高h再除以2。

所以棱锥的表面积S可以表示为：S = n * a² + (n * a * h) / 2这样，我们就得到了计算棱柱和棱锥的体积和表面积的推导公式。

结论：根据上述推导，我们可以通过已知的底面边长、高以及边的个数来计算棱柱和棱锥的体积和表面积。

这些公式提供了便捷的方法来解决计算几何体积和表面积的问题。

注意：本文中所提及的几何体指的是理想情况下的几何体，即没有考虑实际几何体的非完美性。

8.3简单几何体的表面积与体积8.3.1棱柱、棱锥、棱台的表面积和体积学习目标核心素养1.通过对棱柱、棱锥、棱台的研究，掌握棱柱、棱锥、棱台的表面积与体积的求法．(重点)2．会求棱柱、棱锥、棱台有关的组合体的表面积与体积．(难点、易错点)1.借助棱柱、棱锥、棱台的表面积、体积的计算，培养数学运算素养．2．通过对棱柱、棱锥、棱台的体积的探究，提升逻辑推理的素养.1．棱柱、棱锥、棱台的表面积多面体的表面积就是围成多面体各个面的面积的和．2．棱柱、棱锥、棱台的体积棱柱的体积公式V＝Sh(S为底面面积，h为高)；棱锥的体积公式V＝13Sh(S为底面面积，h为高)；棱台的体积公式V＝13h(S′＋S′S＋S)．其中，台体的上、下底面面积分别为S′、S，高为h.思考：简单组合体分割成几个几何体，其表面积不变吗？其体积呢？[提示]表面积变大了，而体积不变．1．棱长为3的正方体的表面积为()A．27B．64C．54D．36C[根据表面积的定义，组成正方体的面共6个，且每个都是边长为3的正方形．从而，其表面积为6×32＝54.]2．长方体同一顶点上的三条棱长分别为1,2,3，则长方体的体积与表面积分别为( )A ．6,22B ．3,22C ．6,11D ．3,11A [V ＝1×2×3＝6，S ＝2(1×2)＋2(1×3)＋2(2×3)＝22.] 3．棱长都是3的三棱锥的表面积S 为 ．93 [因为三棱锥的四个面是全等的正三角形，所以S ＝4×34×32＝9 3.]简单几何体的表面积【例1】 现有一个底面是菱形的直四棱柱，它的体对角线长为9和15，高是5，求该直四棱柱的侧面积．[解] 如图，设底面对角线AC ＝a ，BD ＝b ，交点为O ，对角线A 1C ＝15，B 1D ＝9，∴a 2＋52＝152，b 2＋52＝92， ∴a 2＝200，b 2＝56.∵该直四棱柱的底面是菱形， ∴AB 2＝⎝ ⎛⎭⎪⎫AC 22＋⎝ ⎛⎭⎪⎫BD 22＝a 2＋b 24＝200＋564＝64，∴AB ＝8.∴直四棱柱的侧面积S ＝4×8×5＝160.求几何体的表面积问题，通常将所给几何体分成基本几何体，再通过这些基本几何体的表面积进行求和或作差，从而获得几何体的表面积，另外有时也会用到将几何体展开求其展开图的面积进而得表面积．1．侧面都是等腰直角三角形的正三棱锥，底面边长为a 时，该三棱锥的表面积是( )A.3＋34a 2B.34a 2C.3＋32a 2D.6＋34a 2A [∵侧面都是等腰直角三角形，故侧棱长等于22a ， ∴S 表＝34a 2＋3×12×⎝ ⎛⎭⎪⎫22a 2＝3＋34a 2.]简单几何体的体积【例2】 三棱台ABC -A 1B 1C 1中，AB ∶A 1B 1＝1∶2，求三棱锥A 1-ABC ，三棱锥B -A 1B 1C ，三棱锥C -A 1B 1C 1的体积之比．[解] 设三棱台的高为h ，S △ABC ＝S ，则S △A 1B 1C 1＝4S . ∴VA 1-ABC ＝13S △ABC ·h ＝13Sh ， VC -A 1B 1C 1＝13S △A 1B 1C 1·h ＝43Sh .又V台＝13h(S＋4S＋2S)＝73Sh，∴VB-A1B1C＝V台－VA1-ABC－VC-A1B1C1＝73Sh－Sh3－4Sh3＝23Sh，∴体积比为1∶2∶4.求几何体体积的常用方法2．如图，正方体ABCD-A1B1C1D1的棱长为1，E，F分别为线段AA1，B1C 上的点，则三棱锥D1-EDF的体积为．16[利用三棱锥的体积公式直接求解．VD1-EDF＝VF-DD1E＝13S△D1DE·AB＝13×12×1×1×1＝16.]棱台与棱锥之间关系的综合问题是下底面中心)上底面边长为6，高和下底面边长都是12，求它的侧面积．[解] 如图，E ，E 1分别是BC ，B 1C 1的中点，O ，O 1分别是下、上底面正方形的中心，则O 1O 为正四棱台的高，则O 1O ＝12.连接OE ，O 1E 1， 则OE ＝12AB ＝12×12＝6， O 1E 1＝12A 1B 1＝3.过E 1作E 1H ⊥OE ，垂足为H ， 则E 1H ＝O 1O ＝12，OH ＝O 1E 1＝3， HE ＝OE －O 1E 1＝6－3＝3. 在Rt △E 1HE 中，E 1E 2＝E 1H 2＋HE 2＝122＋32＝32×17， 所以E 1E ＝317.所以S 侧＝4×12×(B 1C 1＋BC )×E 1E ＝2×(6＋12)×317＝10817.在本例中，把棱台还原成棱锥，你能利用棱锥的有关知识求解吗？[解] 如图，正四棱台的侧棱延长交于一点P .取B 1C 1，BC 的中点E 1，E ，则EE 1的延长线必过P 点(以后可以证明)．O 1，O 分别是正方形A 1B 1C 1D 1与正方形ABCD 的中心．由正棱锥的定义，CC 1的延长线过P 点，且有O 1E 1＝12A 1B 1＝3，OE ＝12AB ＝6， 则有PO 1PO ＝O 1E 1OE ＝36， 即PO 1PO 1＋O 1O＝12.所以PO 1＝O 1O ＝12.在Rt △PO 1E 1中，PE 21＝PO 21＋O 1E 21＝122＋32＝32×17，在Rt △POE 中，PE 2＝PO 2＋OE 2＝242＋62＝62×17， 所以E 1E ＝PE －PE 1＝617－317＝317. 所以S 侧＝4×12×(BC ＋B 1C 1)×E 1E ＝2×(12＋6)×317＝10817.解决有关正棱台的问题时，常用两种解题思路：一是把基本量转化到直角梯形中去解决；二是把正棱台还原成正棱锥，利用正棱锥的有关知识来解决．1．棱柱、棱锥、棱台的表面积分别是它们侧面展开图的面积，因此弄清侧面展开图的形状及侧面展开图中各线段的长，是掌握它们的表面积有关问题的关键．2．计算棱柱、棱锥、棱台的体积，关键是根据条件找出相应的底面面积和高，要充分运用多面体的有关截面，将空间问题转化为平面问题．3．在几何体的体积计算中，注意体会“分割思想”、“补体思想”及“等价转化思想”．1．判断正误(1)锥体的体积等于底面积与高之积．()(2)台体的体积，可转化为两个锥体体积之差．()(3)正方体的表面积为96，则正方体的体积为64.()[答案](1)×(2)√(3)√2．如图所示，正方体ABCD-A1B1C1D1的棱长为1，则三棱锥D1-ACD的体积是()A.16 B.13C.12D．1A[三棱锥D1-ADC的体积V＝13S△ADC×D1D＝13×12×AD×DC×D1D＝13×12＝16.]3．已知高为3的棱柱ABC-A1B1C1的底面是边长为1的正三角形(如图)，则三棱锥B1-ABC的体积为()A.14 B.12C.36 D.34[答案]D4．把一个棱长为a的正方体，切成27个全等的小正方体，则所有小正方体的表面积为．18a2[原正方体的棱长为a，切成的27个小正方体的棱长为13a，每个小正方体的表面积S1＝19a 2×6＝23a2，所以27个小正方体的表面积是23a2×27＝18a2.]5．如图所示，三棱锥的顶点为P，P A，PB，PC为三条侧棱，且P A，PB，PC两两互相垂直，又P A＝2，PB＝3，PC＝4，求三棱锥P-ABC的体积V.[解]三棱锥的体积V＝13Sh，其中S为底面积，h为高，而三棱锥的任意一个面都可以作为底面，所以此题可把B看作顶点，△P AC作为底面求解．故V＝13S△P AC·PB＝13×12×2×4×3＝4.。

平面几何中的棱锥和棱锥的表面积和体积平面几何中，棱锥是一种常见的三维图形，由一个多边形底面和若干个共同顶点围成的锥形物体。

棱锥是我们日常生活中常见的物体，如华盛顿纪念碑、埃菲尔铁塔等，均是棱锥的形式。

棱锥的结构棱锥由一个多边形底面和若干个共同顶点围成的锥形物体。

多边形底面顶点个数为n，棱锥的高为h，共同顶点到底面中心点的距离为l，依据底面不同，棱锥的结构也有所不同。

如图所示，一个三角形底面的棱锥结构。

棱锥的表面积棱锥的表面积包括侧棱面积和底面积两部分。

侧棱面积的计算公式为：S1 = 1/2 × p × l其中p为棱锥的底面周长，l为共同顶点到底面的距离。

底面积的计算公式为：S2 = n × l × r其中n为底面的边数，l为边长，r为底面的外接圆半径。

因此，棱锥的表面积公式为：S = S1 + S2 = 1/2 × p × l + n × l × r棱锥的体积棱锥的体积是指棱锥所占据的空间的大小，计算公式为：V = 1/3 × S2 × h因此，棱锥的体积公式为：V = 1/3 × n × l × r × h棱锥的应用棱锥在各个领域中具有广泛的应用，如在建筑工程中，棱锥形式的建筑是旅游景点的重要标志，如我国的春熙路太古里、沈阳太阳岛水上乐园等。

同时，棱锥在数学学科中也有着重要的地位，其形态与性质被广泛运用，例如在微积分中，黎曼积分的定义用到了棱锥的体积公式，而在向量分析中，棱锥模型也被用于定义Delaunay三角剖分的概念。

总结在生活和学习中，我们常常需要计算棱锥的表面积、体积等数值来解决某些实际问题，如在建筑工程中计算棱锥的空间大小来评估建筑成本，在数学学科中通过棱锥的定义与性质演绎出更多有趣且有用的概念和定理。

因此，了解棱锥的结构、特点、公式与应用是很有必要的。

棱台的体积与表面积棱台是一种具有棱角的多面体，由一个上底面、底面到上底面的棱以及连接底面和上底面的侧面构成。

在几何学中，计算棱台的体积与表面积是非常常见的问题。

本文将详细介绍如何计算棱台的体积与表面积，并给出相关的数学公式和实际应用。

一、棱台的定义与性质棱台是由一个上底面和一个底面构成的多面体，底面和上底面都是圆形或多边形，并通过一系列的侧面连接起来。

根据侧面的形状，棱台可以分为正棱台和斜棱台两种。

对于正棱台，底面和上底面都是正多边形，而且侧面都是等腰三角形。

斜棱台则没有这些限制，底面和上底面可以是任意形状的多边形，侧面也不一定是等腰三角形。

无论是正棱台还是斜棱台，其体积和表面积的计算都是基于底面的形状和侧面的长度。

二、计算正1. 正棱台的体积公式设正棱台的底面的边长为a，上底面的边长为b，棱台的高为h，则正棱台的体积V可以通过以下公式计算：V = (1/3) * h * (a^2 + a*b + b^2)其中，^表示乘方运算。

2. 正棱台的表面积公式正棱台的表面积A可以通过以下公式计算：A = 底面积 + 上底面积 + 侧面积底面积 = a^2上底面积 = b^2侧面积 = (1/2) * 周长 * h其中，周长为底面的边长乘以底面的边数。

三、实际应用举例计算棱台的体积与表面积在实际中有着广泛的应用。

举个例子，如果我们要购买一个水箱，需要知道水箱的容积大小，以确定是否适用于存储所需的水量。

而水箱的形状可能就近似于一个棱台，通过计算其体积，可以得知其最大的存水量。

另外，棱台的表面积计算也可以应用于建筑工程。

在建造一个有规则形状的建筑物时，如一个多层平台或塔楼，我们可以使用棱台的表面积公式来确定所需的材料长度和面积，以便提前做好准备。

四、总结通过本文的介绍，我们了解了棱台的定义、性质以及如何计算其体积与表面积。

对于正棱台，我们可以利用相应的公式进行计算，以满足实际应用的需求。

此外，棱台的计算方法也可以应用于其他几何体，如棱锥和棱柱等。

棱台的表面积公式：S圆台表=π(r+R)l+πr^2+πR^2。

棱台的体积取决于两底面之间的距离（棱台的高），以及原来棱锥的体积。

设h为棱台的高，为棱台的上下底面积，V为棱台的体积。

由于棱台是由一个平面截去棱锥的一部分（也就是和原来棱锥相似的一个小棱锥）得到。

所以计算体积的时候，可以先算出原来棱锥的体积，再减去和它相似的小棱锥的体积。

棱锥被平行于底面的平面所截时，截面的面积与底面面积的比，等于小棱锥和原棱锥的高的比的平方。

假设原棱锥的高是H，那幺小棱锥的高是H-h。

正棱台的性质：
（1）正棱台的侧棱相等，侧面是全等的等腰梯形。

各等腰梯形的高相等，它叫做正棱台的斜高。

（2）正棱台的两底面以及平行于底面的截面是相似正多边形。

（3）正棱台的两底面中心连线、相应的边心距和斜高组成一个直角梯形；两底面中心连线、侧棱和两底面相应的半径也组成一个直角梯形。