则
lim f [ ( k ) , ( k ) ]
0 k 1
n
n
注意 2 (t ) 2 (t ) 连续
lim f [ ( k ) , ( k ) ]
0 k 1
因此
说明:
(1) sk 0, t k 0, 因此积分限必须满足 !
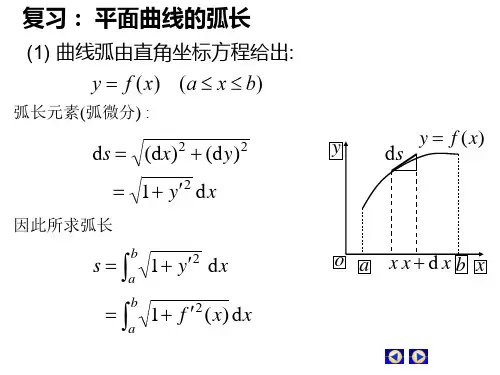
弧长元素(弧微分) :
ds (dx) 2 (d y ) 2
2 (t ) 2 (t ) d t
因此所求弧长
s
2 (t ) 2 (t ) d t
(3) 曲线弧由极坐标方程给出:
令 x r ( ) cos , y r ( ) sin , 则得
弧长元素(弧微分) :
ds [ x( )]2 [ y ( )]2 d
r 2 ( ) r 2 ( ) d
因此所求弧长
s
r 2 ( ) r 2 ( ) d
第十章 曲线积分与曲面积分
积分学 定积分 二重积分 三重积分 曲线积分 曲面积分
积分域
区间域
取极限 W lim [ P ( i , i ) xi Q( i , i ) yi ]. 0
i 1
n
精确值
2. 定义. 设 L 为xoy 平面内从 A 到B 的一条有向光滑
弧, 在L 上定义了一个向量函数
若对 L 的任意分割和在局部弧段上任意取点,
0
极限
L L
( 3) f ( x , y )ds f ( x , y )ds f ( x , y )ds.
L L1 L2
( L L1 L2 ).
( s 为曲线弧 L 的长度)