关于经纬仪角度测量误差减弱措施的论证
- 格式:pdf
- 大小:312.53 KB
- 文档页数:3

浅谈角度测量的误差分析及注意事项摘要:本文简述了角度测量过程中产生的误差,并进行分析及提出其产生原因和减小、消除角度测量误差的方法,对于角度测量过程中的注意事项也做了简单论述。
关键词:角度测量误差分析精度角度测量的误差主要来源于仪器误差、观测误差以及外界条件的影响三个方面。
认真分析这些误差,找出消除或减小误差的方法,从而可以提高观测精度。
一、角度测量的误差1、仪器误差仪器误差主要包括仪器制造加工不完善所引起的误差和仪器校正不完善所引起的误差,主要有视准轴误差、横轴误差、竖轴误差、度盘偏心差等。
(1)视准轴误差视准轴误差是由于视准轴不垂直横轴引起的水平方向读数存在的误差。
随垂直角增大而增大。
由于盘左、盘右观测时该误差的符号相反,因此可以采用盘左、盘右观测取平均值的方法予以消除。
(2)横轴误差横轴误差是由于横轴与竖轴不垂直引起的水平方向读数存在的误差。
随垂直角增大而增大,对两等高目标观测时误差为0。
由于盘左、盘右观测时该误差的符号相反,因此可以采用盘左、盘右观测取平均值的方法予以消除。
(3)竖轴误差竖轴误差是由于水准管轴不垂直于竖轴,或水准管轴不水平而引起的误差。
随垂直角增大而增大,与横轴所处的方向有关。
竖轴误差只能通过校正尽量减少残余误差。
(4)度盘偏心差经纬仪照准部旋转中心与水平度盘分划中心不完全重合而存在的误差。
随照准方向而异,照准方向垂直于偏心方向时对水平方向读数影响最大。
度盘偏心差可以采用盘左、盘右观测取平均值的方法予以消除。
(5)度盘刻画不均匀误差由于度盘刻画不均匀引起的方向读数误差。
度盘制造时产生,可以通过配置度盘各测回起始读数的方法,使读数均匀的分布在度盘各个区域而予以减小。
(6)竖盘指标差由于竖盘指标水准管工作状态不正确,导致竖盘指标没有处在正确的位置,产生读数误差,竖盘指标差只影响对竖直角的测量。
竖盘指标差可以采用盘左、盘右观测取平均值的方法予以消除。
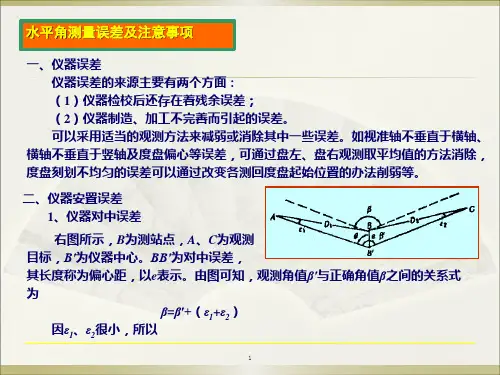
2、观测误差(1)对中误差安置经纬仪没有严格对中,使仪器中心与测站中心不在同一铅垂线上引起的角度误差,称对中误差。

角度测量及其误差控制发表时间:2010-08-18T15:35:30.233Z 来源:《中小企业管理与科技》2010年6月上旬刊供稿作者:董玉启张泽辉[导读] 角度测量作为测量工作的基本内容之一,有其独特的优势董玉启张泽辉(天津二十冶建设有限公司)摘要:角度测量作为测量工作的基本内容之一,有其独特的优势。
但在实际测量的过程中,由于种种因素的影响,不可避免的会产生测角误差。
虽然无法彻底的消除其影响,但是可以采取一些有效的措施,将测角误差削弱至可以忽略的程度,从而测量精度和质量。
关键词:角度测量误差消减 0 引言角度测量是测量的基本工作之一。
在测量工作中,有时候为了确定地面上点的位置,这就需要测量测量竖直角和水平角。
在同一个竖直平面内,水平线与视线之间的夹角即为竖直角,通常用字母a 表示。
水平角指的是地面上两条相交的直线在水平面上的投影之间的夹角,一般用字母β表示。
这些角度值在理论上可以达到非常精确,但是在实际测量的过程中,由于各种因素的影响,不可避免的会产生误差,从而导致测量结果不理想。
因此,采取一些有效的措施将测量误差的影响降低到最小的程度是十分必要的。
1 角度测量的常用仪器和方法角度测量最主要的仪器是经纬仪,它既可以测量竖直角和水平角,也可进行高程测量和距离测量。
按测角精度的不同,经纬仪可以分成DJ6、DJ2、DJ1和DJ07等系列。
在进行竖直角的测量时,需要在经纬仪的横轴一端放置一个竖直刻度盘,利用望远镜瞄准目标读取竖盘读数,便可计算得出竖直角。
进行水平角的测量时,可以采用方向观测法或是测回法。
方向观测法适用于当对某一个测站点上需要测量的方向数大于2的情况。
测回法则适用于测量两个不同方向之间的水平角。
2 角度测量的误差分析 2.1 测量误差的分类测量误差按照性质可分为系统误差、粗差、偶然误差三类。
①系统误差。
系统误差是指在相同的观测条件下,对某一具体量进行一系列的观测,观测过程中产生的误差在符号和数值上均相同,或呈现一定规律的变化趋势。


减小误差的方法在科学研究和工程实践中,减小误差是非常重要的一项工作。
误差的存在会影响到实验结果的准确性,甚至可能导致错误的结论和决策。
因此,我们需要采取一些方法来减小误差,提高实验和工程的可靠性和准确性。
首先,选择合适的仪器和设备是减小误差的关键。
优质的仪器和设备能够提供更加准确的测量结果,减小系统误差的产生。
因此,在实验和工程中,我们应该选择精度高、稳定性好的仪器和设备,以确保测量数据的准确性和可靠性。
其次,严格控制实验条件和环境也是减小误差的重要手段。
实验条件和环境的变化会对测量结果产生影响,因此我们需要尽量消除这些影响,确保实验条件和环境的稳定性。
在实验中,我们可以通过控制温度、湿度、光照等因素,以及采取隔离措施,来减小外界因素对实验结果的影响,从而提高测量的准确性。
另外,合理设计实验方案和工程流程也是减小误差的重要策略。
在实验和工程中,我们需要充分考虑到各种可能的误差来源,合理设计实验方案和工程流程,以减小误差的产生。
比如,在实验设计中,我们可以采取重复测量、对照实验等方法,以消除随机误差的影响;在工程设计中,我们可以采取多重检测、多重验证等手段,以减小系统误差的产生。
通过合理设计实验方案和工程流程,我们能够更好地控制误差,提高测量和工程的准确性。
此外,及时校准和维护仪器设备也是减小误差的有效途径。
仪器设备在使用过程中会出现漂移、老化等现象,导致测量结果的偏差和误差。
因此,我们需要定期对仪器设备进行校准和维护,及时发现并修复问题,以确保仪器设备的准确性和可靠性。
总之,减小误差是科学研究和工程实践中非常重要的一项工作。
通过选择合适的仪器设备、严格控制实验条件和环境、合理设计实验方案和工程流程,以及及时校准和维护仪器设备,我们能够有效地减小误差,提高测量和工程的准确性和可靠性。
希望以上方法能够对大家在科学研究和工程实践中减小误差有所帮助。


角度测量的误差分析及注意事项一、角度测量的误差角度测量的误差主要来源于仪器误差、人为操作误差以及外界条件的影响等几个方面。
认真分析这些误差,找出消除或减小误差的方法,从而提高观测精度。
由于竖直角主要用于三角高程测量和视距测量,在测量竖直角时,只要严格按照操作规程作业,采用测回法消除竖盘指标差对竖角的影响,测得的竖直角值即能满足对高程和水平距离的求算。
因此,下面只分析水平角的测量误差。
(一)仪器误差1.仪器制造加工不完善所引起的误差如照准部偏心误差、度盘分划误差等。
经纬仪照准部旋转中心应与水平度盘中心重合,如果两者不重合,即存在照准部偏心差,在水平角测量中,此项误差影响也可通过盘左、盘右观测取平均值的方法加以消除。
水平度盘分划误差的影响一般较小,当测量精度要求较高时,可采用各测回间变换水平度盘位置的方法进行观测,以减弱这一项误差影响。
2.仪器校正不完善所引起的误差如望远镜视准轴不严格垂直于横轴、横轴不严格垂直于竖轴所引起的误差,可以采用盘左、盘右观测取平均的方法来消除,而竖轴不垂直于水准管轴所引起的误差则不能通过盘左、盘右观测取平均或其他观测方法来消除,因此,必须认真做好仪器此项检验、校正。
(二)观测误差1.对中误差仪器对中不准确,使仪器中心偏离测站中心的位移叫偏心距,偏心距将使所观测的水平角值不是大就是小。
经研究已经知道,对中引起的水平角观测误差与偏心距成正比,并与测站到观测点的距离成反比。
因此,在进行水平角观测时,仪器的对中误差不应超出相应规范规定的范围,特别对于短边的角度进行观测时,更应该精确对中。
2.整平误差若仪器未能精确整平或在观测过程中气泡不再居中,竖轴就会偏离铅直位置。
整平误差不能用观测方法来消除,此项误差的影响与观测目标时视线竖直角的大小有关,当观测目标与仪器视线大致同高时,影响较小;当观测目标时,视线竖直角较大,则整平误差的影响明显增大,此时,应特别注意认真整平仪器。
当发现水准管气泡偏离零点超过一格以上时,应重新整平仪器,重新观测。


电子经纬仪的检定与误差解析电子经纬仪不仅能作为测角仪器单独完成测量工作,还能与电子手簿、激光测距仪等组成全站仪,或与激光测距机、卫星定位仪、陀螺仪等组成测地系统。
本文详细分析了电子经纬仪的误差成因,旨在提高电子经纬仪的测量精度。
标签:电子经纬仪;鉴定范围;误差解析计算机技术与微电子技术的快速发展,为传统测绘仪器带来了革命性的变化,电子经纬仪正是在这种科技的冲击下而诞生的一种测量仪器,被广泛应用在建筑、军事等行业,极大提高了现代测绘技术水平。
1.电子经纬仪电子经纬仪是一款集光学、电子、机械、计算为一体的高精度光学测量仪器,其在光学经纬仪的基础上增加了自动化智能技术、滤波技术以及电子细分控制技术等,能够对测量数据进行智能读取,除被广泛应用在公路、铁路、水利等工程的测量中,还可以用于大型建筑、设备的实地安装地形测量。
常见的电子经纬仪主要由:照准部、望远镜、测微器系统、水准器、基座及脚螺旋、光栅盘或光学码盘、读数面板、光学对点器,九大部分组成,具有较高的抗振能力、稳定性、可靠性,以及耗电小、寿命长、温度影响小等优点,适用于各种地形测量、地籍测量、工程测量。
2.进行电子经纬仪检定的主要内容电子经纬仪是在光学经纬仪基础发展而来,为进一步提升其精确度,我们应熟悉并掌握电子经纬仪的检定工作内容。
1)水准器轴与竖轴的垂直度;2)望远镜竖丝铅垂度;3)望远镜视轴对横轴的垂直度;4)横轴误差;5)照准差;6)竖轴误差;7)光学对中器视轴与竖轴重合度;8)望远镜调焦视轴变动误差;9)一测回水平方向标准偏差。
3.电子经纬仪的误差分析电子经纬仪主要用于边角的角度测量,测量误差是比照国家标准仪器精度来判断的,而国家标准仪器精度指的是一测回水平方向的标准误差。
在對电子经纬仪进行误差测量时,需要首先将电子经纬仪的望远镜对准实现选取的目标点A,获得对应角度的测量数值,然后对转目标点B,继续获得相应角度的测量数值,A、B两点测量数值间的误差为目标点间的夹角。

一、实习目的与意义本次实训旨在使学生熟练掌握经纬仪的使用方法,学会通过经纬仪进行角度测量,并了解角度测量的基本原理和误差分析。
通过本次实训,学生可以巩固课堂所学知识,提高动手操作能力和实际解决问题的能力。
二、实习内容与方法1. 实习内容(1)了解经纬仪的结构、工作原理及使用方法。
(2)掌握经纬仪对中、整平、瞄准和读数的方法。
(3)学会使用经纬仪进行水平角和竖直角的测量。
(4)掌握角度测量的误差分析及数据处理方法。
2. 实习方法(1)理论讲解:由教师讲解经纬仪的结构、工作原理、使用方法、角度测量的误差分析及数据处理方法等。
(2)实际操作:学生在教师的指导下,进行经纬仪的对中、整平、瞄准和读数等操作,并测量水平角和竖直角。
(3)数据处理:对所测量的角度数据进行整理、分析,计算误差。
三、实习过程1. 实习准备(1)熟悉实习内容及要求。
(2)了解经纬仪的结构、工作原理及使用方法。
(3)准备好实习所需的仪器和工具。
2. 实习操作(1)对中:将经纬仪放置在测量点,调整仪器,使照准轴与地面垂直。
(2)整平:调整仪器,使照准轴与水平面平行。
(3)瞄准:将望远镜对准目标点,使目标点位于十字丝中心。
(4)读数:读取望远镜中十字丝的水平方向和竖直方向的读数。
(5)水平角测量:测量目标点与起始方向之间的水平角。
(6)竖直角测量:测量目标点与水平面之间的竖直角。
3. 数据处理(1)整理测量数据,计算水平角和竖直角的平均值。
(2)分析测量误差,计算误差来源及误差大小。
(3)对测量结果进行评价。
四、实习结果与分析1. 实习结果(1)熟练掌握了经纬仪的使用方法。
(2)能够正确进行水平角和竖直角的测量。
(3)学会了角度测量的误差分析及数据处理方法。
2. 实习分析(1)实习过程中,学生认真操作,积极思考,提高了实际操作能力。
(2)通过误差分析,学生了解了角度测量的误差来源及影响,提高了对测量结果评价的能力。
(3)本次实习使学生巩固了课堂所学知识,为今后从事测绘工作打下了基础。

3 经纬仪及角度测量3.1 水平角测量原理3.2 DJ6型光学经纬仪3.3 水平角测量3.4 竖直角测量3.5 角度测量中误差产生的原因及消除方法3 经纬仪及角度测量角度测量是确定地面点位的基本测量工作之一,包括水平角测量和垂直角测量。
经纬仪是进行角度测量的主要仪器。
垂直角:观测水平角的经纬仪必须具备的条件:1)有能够水平安置的刻度圆盘和能够精确读取度盘读数的读数装置;2)有能够在水平方向和竖直方向转动的瞄准设备,以精确瞄准不同方向、不同高度和不同距离的目标;3)有能够将度盘的中心安置在所测角顶点的铅垂线方向上的设备。
3.2 DJ6型光学经纬仪D:大地测量仪器J:经纬仪数字:表示精度按测角精度:DJ07DJ1,DJ2,DJ6等几种类型。
3.2.1.1 照准部1)望远镜望远镜是用作精确瞄准目标的。
它和水平轴连接在一起,可以绕水平轴在竖直面内上下任意转动。
包括:物镜,目镜,内调焦镜,十字丝板2)竖直度盘。
用来测量竖直角的度盘装置。
3)照准部水准管。
照准部上有一个水准管和一个圆水准器。
圆水准器用作粗略整平,水准管用作精确整平仪器。
4)光学读数系统。
起改变光路的作用。
5)读数显微镜。
把水平度盘和竖直度盘的读数窗口放大,进行读数。
6)内轴。
整个照准部可在轴座内任意地作水平方向的旋转。
照准部下部装有水平制动扳钮和水平微动螺旋。
3.2.1.2 水平度盘部分1)水平度盘。
顺时针0°~360 °全圆注记, 不能随便转动。
2)度盘变换手轮。
可以调整水平度盘的当前位置的刻度值。
3)外轴。
连接度盘与基座。
3.2.1.3 基座三个脚螺旋用于整平仪器(粗平)连接仪器与三脚架3.2.2 电子经纬仪随着科技发展,近几年电子经纬仪发展迅猛,标志着经纬仪发展到一个新的阶段,并为测量工作的自动化创造了有利的条件。
电子经纬仪测角精度高,能够自动显示角度值,具有光学经纬仪类似的结构特征,其不同点在于读数系统,光学经纬仪采用光学度盘和人工读数,电子经纬仪则采用光电扫描度盘和自动读数系统。
使用经纬仪进行方位角测量的方法与技巧导言:方位角测量是地理定位和导航中非常重要的一项技术。
随着现代科技的发展,人们已经习惯于使用GPS等便捷工具来导航和定位。
然而,在某些情况下,依靠传统的手动测量方法可能会更准确和可靠。
本文将介绍使用经纬仪进行方位角测量的方法与技巧。
一、什么是经纬仪?经纬仪是一种常见的测量工具,用于测量距离、角度和方位角。
它由一个具有刻度的旋转盘和一个可调节的目镜组成。
通过观测目标物体和旋转盘上的固定点,可以测量方位角。
二、准备工作在使用经纬仪进行方位角测量前,有一些准备工作是必要的。
首先,需要选择一个合适的观测点,在该点上放置经纬仪。
观测点应尽可能稳固,以确保测量的准确性。
其次,需要清除观测方向上的障碍物,以保证目标物体的可见性。
最后,需要确定观测时的天气条件。
在大风、强日照或恶劣天气情况下,测量结果可能受到干扰,因此需要选择适当的观测时间。
三、确定初始指向在测量方位角前,需要先确定一个初始的指向。
通常,可以通过观测目标物体的方位角或与目标物体相邻的地物来确定初始指向。
例如,可以通过观测北极星的位置来确定北方的方向。
四、目标物体的观测与记录当确定了初始指向后,可以开始观测目标物体并记录测量结果。
首先,将目标物体置于目镜的中心,并将视线对准目标物体。
然后,以目标物体为中心,旋转经纬仪的旋转盘,并同时观察刻度盘上的读数。
当目标物体恰好位于探针中心时,刻度盘上的读数即为目标物体的方位角。
五、准确性与精度的控制在进行方位角测量时,准确性和精度是非常重要的。
为了提高准确性,可以采取以下措施。
首先,确保经纬仪的仪器精度。
不同的经纬仪在刻度和读数精度方面可能存在差异,因此在选购和使用时应注意其技术参数。
其次,保持仪器的水平和稳固。
经纬仪需要放置在平坦的地面上,并使用调整脚等工具来保持其水平。
最后,进行多次测量并取平均值。
重复测量同一目标物体多次,并计算平均值,可以减小因个体测量误差而产生的偏差。
经纬仪水平角测量仪器误差探析仪器的制造和安装不论如何严格要求,也不可能百分之百地达到仪器各部件及其相互几何关系的要求,伴随使用中的磨损、变形及外界因素的影响,测定结果不可避免地存在误差,这就是所谓的仪器误差。
三轴误差(视准轴误差、水平轴倾斜误差、垂直轴倾斜误差)、照准部旋转误差以及分划误差(水平度盘分划误差、测微盘分划误差)、光学测微器行差共同组成仪器误差。
本文将主要阐述和分析仪器误差的成因、控制措施和消减办法。
1 三轴误差的影响1.1 视准轴误差产生视准轴误差的原因是安装和调整不规范,望远镜的十字丝中心不在正确的位置,视准轴与水平轴不正交而产生的。
另外,视准轴位置也会因温度的差异引起变化,造成视准轴误差。
视准轴误差对观测方向值的影响,在望远镜纵转前后,大小相等,符号相反。
因此,可利用取盘左与盘右的平均数消除。
1.2 水平轴倾斜误差水平轴倾斜误差是在水平轴与视准轴正交、垂直轴与测站铅垂线一致的前提下,仅由于水平轴与垂直轴不正交使水平轴倾斜一个小角造成的。
水平轴倾斜误差出现的原因:未按规范正确安装、调整仪器,造成仪器水平轴两支架不等高或軸两端的直径不等。
在盘左、右读数中,取平均值来消除水平轴倾斜误差对观测值的影响。
1.3 垂直轴倾斜误差仪器三轴间关系均已符合要求时,仪器水平未严格整置,使仪器垂直轴和测站铅垂线间有一个微小的偏离角度,称垂直轴倾斜误差。
结果视准轴(与水平轴正交)也偏离了正确位置,在其绕水平轴俯仰时的照准面形成了倾斜照准面,而不是要求的垂直照准面,造成了水平方向观测的误差。
该误差不像水平轴倾斜误差通过盘左盘右观测取平均能抵消,要仔细整平。
2 照准部旋转误差在观测过程中仪器转动可能产生一些误差。
2.1 弹性带动误差轴套和垂直轴间存在摩擦力使照准部转动时,仪器的基座局部出现弹性扭转,水平度盘因摩擦力被带动发生微小的方位变动。
需要克服轴与轴套间互相的惯性阻力,弹性带动主要发生在照准部转动起始时,照准部转动过程中,摩擦力较小。
降低测量误差的方法有哪些?
降低测量误差的方法有多种,主要包括:
1. 校准测量工具:工具在使用过程中受各种因素印象其精度会发生改变,因而需要适时校正,以提高测量准确度。
2. 选用高精度测量工具:选用精度高(分度值小)的仪器可以减小误差,如采用更精确的刻度尺、游标卡尺、量筒等。
3. 改进测量方法:如采用累积法,比如测出用线悬挂的小球30次摆动所用的时间,除以30得到小球摆动所用时间,可减小测量误差。
或者采用放大法,通过放大镜等将微小的变化放大观察,有利于减小误差。
4. 多次测量求平均值:为了减小由于测量人对于测量时估计数字方面的误差,可以多次测量求平均值。
综上所述,通过校准测量工具、选用高精度测量工具、改进测量方法和多次测量求平均值等方法可以有效降低测量误差。
在实际应用中,应根据具体情况选择合适的方法,以提高测量的准确性和可靠性。
关于经纬仪角度测量误差减弱措施的论证发表时间:2014-09-11T14:44:30.043Z 来源:《科学与技术》2014年第6期下供稿作者:王耀明[导读] 仪器机械传动误差对测角误差的影响分析机械传动误差是在观测过程中操作仪器所产生的误差。
红河州南洞泵站工程管理处王耀明一、绪论角度测量是确定地面点位三要素(角度、距高、高程)的基本测量工作之一。
它广泛应用在工程建设中的定位标定中,经纬仪是主要测角的仪器,三角网、支导线推算元素的精度,除了与图形结构有关外,主要取决于测角的精度,而角度是由两个方向组成的,在测角过程中有各种各样的误差来源,这些误差来源对水平角的观测精度又有着不同的影响。
欲提高测角精度,必须减弱经纬仪方向观测的各种误差来源,才能有效提高水平角精度。
二、经纬仪角度测量的误差来源影响经纬仪角度观测精度的因素很多,但是其主要来源因素有四种,如仪器误差的来源、观测误差的来源、测角方法误差的来源、外界条件引起的误差来源。
三、经纬仪角度测量误差来源分析及其减弱措施3-1仪器本身误差来源对角度测量误差影响分析由于仪器从零件制造到整体装配,都会存在一系列的误差,从而损坏仪器正确结构。
其次,随着仪器使用时间年限增加的影响,仪器误差也会增大,主要使仪器误差带来两方面的测角影响,一方面是三轴几何关系不正确所产生的几何结构误差,即视准轴误差、水平轴倾斜误差、垂直轴倾斜误差。
另一方面是仪器制造、校准不完善,传动磨损等原因所产生的机械结构误差,即度盘和测微尺分划误差、螺旋和轴与轴套的机械误差、照准部和度盘偏心的误差、光学测微器的行差、传动误差,下面将仪器误差的产生和影响测角精度分析如下:(一)三轴几何关系不正确所产生的几何结构误差1、视准轴误差对测角误差的影响分析当视准轴发生斜偏时,视准轴不垂直于水平轴,望远镜绕水平轴旋转时,视准轴扫出的面与正确时扫出的视准面发生偏移,视准面不再是平面,而是一个圆锥面,设视准轴误差为C,观测垂直角 a 目标时,所产生的测角误差为△C。
根据视准轴误差球面直角三角形可知△C = C/cosα公式。
当用盘左位置观测时,视准误差△C为正,盘右位置观测时,视准轴误差为负,这就是说视准轴误差 C 对观测方向的影响△C,盘左、盘右大小相等、符号相反,所以取盘左、盘右读数的平均值,就可以消除视准轴误差的影响,但是这结论必须在盘左、盘右观测期间保持不变的条件下才是正确的,即一个测回内不得重新调焦,保证视准轴位置不变。
视准轴误差C 对观测方向值的影响随目标垂直角 a 的增大而增加,当观测方向为水平时△C=C。
观测竖角相等的两点间视准轴误差的影响相互抵消。
在观测时,视准轴偏斜误差2C,可以用来检查仪器稳定性和观测成果的质量,只要掌握它的影响规律,就可以用测量方法来减小和消除视准轴误差影响方向观测的精度。
2、水平轴倾斜误差对测角误差的影响分析由于望远镜两侧支架不等高或水平轴两端直径不等,至使水平轴不垂直于竖直轴,发生微小倾斜,产生水平轴误差i,望远镜绕水平轴旋轴时,视准轴所形成的平面不是铅垂面,而是成为倾斜平面,设水平轴倾斜误差为i 观测垂直角a 目标时所产生的测角误差为△i,根据视准面几何关系得到球面直角三角形公式△i= i×tga,为水平轴误差影响方向观测值的误差,从公式可以知它的大小,它不仅与水平轴倾斜角i 的大小有关,而且与照准目标的垂直角a有关,a愈大,△i愈大,a=0时△i=0。
当观测水平位置的目标,横轴倾斜对方向值没有影响,但是,当个别观测方向的垂直角a 比较大时,就应该考虑到正、倒镜数值中,除视准轴偏斜影响以外,还包含水平轴倾斜影响,如果将垂直角大于3°的方向与其它垂直角水平的方向进行2C 互差比较,就不合理了,当照准点方向的垂直角超过 ± 3°时,该方向的2C 互差可按同一观测的时间段内的相邻测回进行比较。
3、垂直轴倾斜误差对测角误差的影响分析若视准轴与水平轴垂直,水平轴就与垂直竖轴垂直,只是垂直竖轴本身不竖直而偏离铅垂位置V,就产生了垂直竖轴误差影响方向观测角度的精度,实质上是由于垂直竖轴倾斜而引起水平轴倾斜所造成的,当旋转照准部对目标进行观测时,水平轴将以倾斜的垂直竖轴为轴,在倾斜面内转动,随着照准部的转动,水平轴的倾斜角不断发生变化。
根据垂直轴倾斜与水平轴几何关系得知,垂直竖轴倾斜误差影响方向值公式△V=V×cosβ×tga,从公式中得知,垂直轴误差对水平角的影响△V,不仅会随观测方向的垂直角 a 增大而增大,而且与水平轴所处的位置有关。
这是不同于水平轴倾斜误差的根本之点,因它产生的水平轴倾斜的方向、盘左盘右时均相同,误差正负号相同,不能用盘左、盘右观测方法改变和清除影响,所以在观测中照准部水准管气泡中心偏离不应超过一格,否则应在测回之间重新整平仪器。
由于垂直轴其倾斜误差对方向观测值的影响△V,随观测目标的垂直角和方位不同而变化,因而各方向误差并不相等,组成角度时也不能得到消除,当照准点的垂直角超过 ±3°时,各测回间应精确整平仪器,使水准气泡居中减小误差影响。
(二)仪器机械传动误差对测角误差的影响分析机械传动误差是在观测过程中操作仪器所产生的误差。
1、照准部转动时的弹性带动误差对测角误差影响分析当照准部转动时,由于照准部的轴心与基座轴套之间有磨擦致使基座部分发生弹性扭曲。
因此与基座相连的水平度盘发生微小的方位变动,当照准部向右时,水平度盘也随之向右被带动一个微小角度,使读数减小,反之,使读数增大,这就给方向观测值带来系统误差。
如果要想消除这种误差的影响,在上半个测回中照准各个目标时,照准部必须沿同一方向转动,以便使各目标所产生的误差符相同,大小近于相等。
这样,在各个方向相减所得的角度中将抵消这种误差的大部份,下半测回必须逆转照准部观测各方向,这样读数平均值中会有效地减弱这种误差的影响。
2、脚螺旋的空隙带动误差对角度误差影响分析由于基座螺旋杆与螺旋窝之间存在微小空隙,当转动照准部时,垂直轴的微小磨擦将带动基座,使螺旋杆逐渐靠近螺旋窝空隙的一侧,直到两者完全接触为止。
在观测过程中,基座与水平度盘就产生微小的方位变动,使读数产生误差,这种误差对变更仪器旋转方向后的第一个照准目标影响最大,对以后其它目标的影响逐渐减小。
要消除减弱这种误差影响,在观测前先将照准部沿着将要旋转的方向转动1—2 周后,再按旋转方向顺序观测,不得作反向旋转,就可以减小这种误差的影响。
3、照准部水平微动螺旋的隙动误差影响分析旋进照准部水平微动螺旋时,靠螺旋杆的压力推动照准部,旋出时,靠弹簧的弹力推动照准部,由于油污阻碍或弹簧老化等原因使弹力减弱,则微动螺旋旋出扣,照准部不能及时转动,微动螺杆顶杆就出现微小空隙,这就使视准轴偏离了原来照准部方向,产生方向值误差。
要消除减小这种误差带来的影响,照准观测方向时应尽量旋进微动螺旋(与弹力作用方向相反)同时要尽量使用微动螺旋的中间部3—2 观测误差对水平角误差的影响分析1、对中误差对水平角误差的影响分析在测站上安置仪器时,若仪器中心不在所测点的同一垂线上,出现对中误差,它对水平角的影响与测站偏心距e,观测边长D,以及观测方向与偏心方向的夹角φ 有关,即ε=p″×e〔sinφ/D1+sin(B-φ)/D2〕。
由对中误差对水平角影响误差公式可知:经纬仪对中误差对测角的影响,决定于所测角度的大小,当其它条件相同,观测近于180°的角时为最大,与此构成此角两边的长度成反比,测角两边长相差的愈大,误差影响愈大。
要减小这种误差的影响,在边长较短且转折角接近180°时,应特别注意提高对中精度,尽量避免长短边测设。
2、整平误差对水平角误差的影响分析由于仪器没有整平将引起垂直轴和水平度盘的倾斜,势必给水平角观测带来误差,主要原因是垂直轴发生倾斜不垂直而造成的。
由于它不能用观测方法来消除,所以作业前必须精确校准照准部水准管轴和竖轴互相垂直关系,作业时认真整平仪器,在一个测回观测过程中气泡不能偏差半格,否则应重新整平后再观测。
3、标杆倾斜误差对水平角误差影响分析观测角度时,常不能直接瞄准观测目标,只能瞄准设在测点上的标杆。
如果标杆发生倾斜,没有铅垂地置于测点上,在实测中所测角值就包含着标杆的倾斜误差,如果测点至目标的距离为D,仪器瞄准标杆位置至测点长为L,标杆倾斜角为β,那么对水平角影响的误差为a″=P/D ×L×cosβ,从公式中我们知道目标偏心误差对水平角的影响与测站距离成反比,与倾角成正比,要减少标杆倾斜误差的影响,观测时必须仔细竖直标杆,并尽可能瞄准标杆底部。
4、瞄准误差与读数误差对水平角误差影响分析影响照准精度的主要因素是:望远镜的放大率、目标与照准标志的形状以及人眼的判别能力,目标影象的亮度和清晰度有关,要减少影响误差,必须选择放大率适中的仪器,选择良好的外界观测条件。
读数误差主要取决于仪器读数设备,照明情况不佳、显微镜的目镜调焦情况、以及观测者的技术不熟练估读的极限误差超限。
3—3 测角方法的误差对水平角误差影响分析角度观测的误差一半来自照准目标不准确、仪器对中不准确以及读数不准确,但是由于观测方法不同,所产生的误差情况也不同。
1、方向观测法误差对水平角影响分析如果在水平角β 测角过程中每次望远镜照准目标的中误差为mv,每次读数之中误差为 mt 根据误差传播定律得每观测一次方向值中的误差为m 方=±(mv2+mt2)1/2。
因为一个角度是两个方向值之差,故方向观测角度的中误差为mβ=±〔2(mv2+mt2)〕1/2 。
2、测回法误差对水平角误差影响分析若对β 角用上述方法以正、到镜观测了一个测回(每半测回起始方向不归零),则一测回角度平均值之中误差为 mβ1= ±〔2(mv2+mt2/2)〕1/2 /21/2 =±(mv2+mt2/2)1/2,用同样的方法β 角观测了n 个测回,测n 个测回角β 平均数均值的中误差为mβ 均 =±〔1/n(mv2+mt2/2)〕1/2 若取两次读数平均值的误差为m0,则 m0=mt/21/2,于是得mβ 均=±〔1/n (mv2+m0)〕1/23、复测法误差对水平角误差影响分析当用复测法对角进行n 次复测时,仍按正、倒镜观测每个方向照准n 次,共照准2n 次,则n 倍角的照准误差为mv2=2nmv2,因读数只读首尾两次,每次均取两次重合读数的中数,则读数中误差为 mt2=2×mt2/2=2m02,n 倍角的观测值为 nβ=C-b+i×360°,故nβ 之误差为:mnβ= ±(mv2+mt2)1/2=±(2nmv2+2m02)1/2 = ±〔2n(mv2+m02/n)〕1/2,而角β的平均值为β=(c-b+i×360°)/n。