例题最大流的标号法

b.终点得到标号，反向追踪即可找到从起点到终点由标号 点及相应的弧连接而成的一条增广链。
(0, +∞)
s (5, 2)
(S+,3)
v1
(7, 5)
(v1-,5)
t
h
18
3．调整过程：
修改流量，其中流量调整量
， mjinj
指增广链上所有点的流量修正量； j
调整方法：
在增广链的正向弧上增加 ；
反向弧上减少 ；
是，则不加标记； 不是，则加标记为(vs+,j)，其中 j =csj-fsj；
✓对反向弧，检查其是否是零流弧？
是，则不加标记； 不是，则加标记为(vs-, j)，其中 j =fsj；
h
17
重复步骤二，但要注意把vs换成已得到标号的点；可能
出现两种结局：
a.标号过程中断，终点得不到标号。说明该网络中不存在 增广链，现行的可行流就是最大流；
h
13
定理8：
可行流f *是最大流，当且仅当 存不 在
关于f *的增广链。
➢思路：可行流f*是最大流<=>不存在关于f*的增广链.
[证] 必要性→ 用反证法。若 f* 是D中的最大流，假定存在关于f* 的增
广链u，令
。那么，由增广链的定义可
知 m ，现令m iu n (c i{ ijn fi* j)m ,u fii* j} n
令 vsV1*（ ; 起点属V 于 1*）点集 若 vi V1*,且 fi*j cij,则令 vj V1*(正向非饱和弧 都 的 属 起 V1于 *)终 若 vi V1*,且 fj*i 0,则令 vj V（ 1* 反向非零弧 都 的 属 起 V1于 *） 终
因D中不存在关于f*的增广链，故必有

最大流量问题（1）流量问题是一类应用极为广泛的问题，例如在交通网络中有人流、车流、货物流，供水网络中有水流，金融系统中现金流，等等。

最大流量问题，是一种组合最优化问题，就是要讨论如何充分利用装置的能力，使得运输的流量最大，以取得最好的效果。

求最大流量的标号算法最早由福特(Ford)和福克逊(Fulkerson)于1956年提出，他们建立的“网络流理论”，是网络应用的重要组成成分。

我们今天介绍最简单的最大流量问题：找出从单个源点到单个目标点之间可以通过的最大流量。

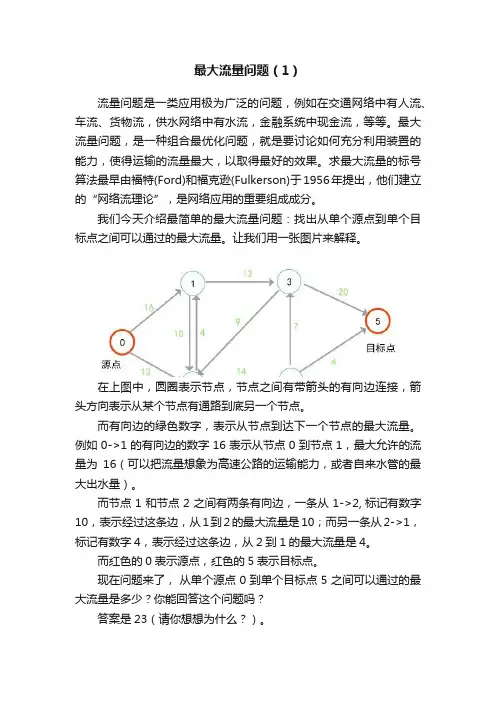
让我们用一张图片来解释。

在上图中，圆圈表示节点，节点之间有带箭头的有向边连接，箭头方向表示从某个节点有通路到底另一个节点。

而有向边的绿色数字，表示从节点到达下一个节点的最大流量。

例如0->1的有向边的数字16表示从节点0到节点1，最大允许的流量为16（可以把流量想象为高速公路的运输能力，或者自来水管的最大出水量）。

而节点1和节点2之间有两条有向边，一条从1->2, 标记有数字10，表示经过这条边，从1到2的最大流量是10；而另一条从2->1，标记有数字4，表示经过这条边，从2到1的最大流量是4。

而红色的0表示源点，红色的5表示目标点。

现在问题来了，从单个源点0到单个目标点5之间可以通过的最大流量是多少？你能回答这个问题吗？答案是23（请你想想为什么？）。

具体的分流的情况如下图所示，其中的粉色数字表示两点之间的实际流量，它必须不大于原来规定的最大流量。

朴素贪婪算法我们先尝试采用朴素的贪婪算法来解决最大流量问题。

从假设每条边的流量都是0开始，采用贪婪算法，逐步增加对应的流量。

也就是从源点s到目标点t的某个路径上逐步增加更多流量（当然必须满足每条边的流量不超过运行的最大流量）。

假设在例子中：E是边的集合f(e)是边对应的流量C(e)是边对应的最大流量s-t路径表示从源点到目标点存在的路径算法的描述如下：1) max_flow = 02) 当存在s-t路径时，对每一条路径重复下面的步骤：a) 采用DFS（深度优先）或BFS（宽度优先）找到从s-t的路径P，并且路径上的每一条边e 都满足 f(e) < C(e)b) 如果找不到路径, 返回 max_flow。

割是分离A和F的弧的集合,若切断一个割的所有弧对应的桥梁, 就可切断A和F之间的线路。切断最小割包含的弧对应的桥 梁，是切断A和F之间线路的桥梁数最少的方法。
由最大流最小割定理，分离A和F的最小割容量等于由A到F的 最大流量 A(0,+) 1,1 2 ,1 1 1, 1,0 2,1 D 2,0 B E C 1,1 2,0 (B,1) (A,1) 1 2, 2,1 F 由上图得知：已标号点为A，B，C，而D，E，F不能获得标 号，从而知道该最大流对应的最小割为{（A，E），（C， D），（C，F）}因此，切断AE，CD，CF三座桥梁，即可阻 止对方部队过河。
3 3 2 v4
割 集 容量 6 7 7 5 11 8 最小割 { (v1, v2) , ( v1, v3) } { (v1, v3) , ( v2, v5) } { (v1, v2 ) , ( v3, v2) , (v3,v4 ) } { (v2, v5) , ( v3, v4) } {(v1, v2) , ( v3, v2),(v4,v2) , (v4,v5)} { (v2 , v5 ) , ( v4 , v5 ) }
• 割中所有弧的容量之和称为该割的容量
C (V1 ,V2 )
( v i , v j )(V1 ,V2 )

c ij
所有割中容量最小的称为最小割
v2 2 v1 4 v3
V1 {v1} {v1,v2} {v1,v3} { v1,v2,v3 } {v1,v3 ,v4 } {v1 ,v2 ,v3, v4} V2 { v2 ,v3 ,v4 , v5 } { v3 ,v4 ,v5 } {v2 ,v4, v5} { v4, v5 } { v2 ,v5 } { v5 }
1,1

2 2
5 6
6 0
7
V6
V 8 V 10
V3
6 10
V5
前向弧： 1 min{Cij fij } 2
后向弧：
2
min{ 1 , 2 } 2
V2
8 8
5 5 3 2 5
1
V4
10 19
4
V1
2 2
5 6
6 0
7
V6
V 8 V 10
而对于实际问题来说，通常需要求最大流．
那么，如何求最大流呢？ 最大流可以从任何一个可行流出发来求．
这需要下面的可扩充路的概念．
定义 6.17 设 { fij }是一组可行流，如果存在一 条从起点V1 到终点V 的路P，满足 ①在P的所有前向弧上 0 fij Cij ( fij Cij ) ( fij 0) ②在P的所有后向弧上 0 fij Cij 则称P是一条关于流 { fij }的可扩充路．
对于P的所有后向弧 (0 fij Cij ) (若P无后向弧，则令 2 ) 令 2 min{ fij }
再令 min{ 1 , 2 }
最后，构造新的可行流 { f ij }, 使得
f ij fij fij
f ij
若弧 (Vi ,Vj )不在路P上 若弧 (Vi ,Vj )是路P的前向弧 若弧 (Vi ,Vj ) 是路P的后向弧
V3 V2
8
8
6 10
V5 V4
5
1
2 5
最大流不唯一
7
3 0 6 6
19
4
V1
2 2
6 3
7
V6

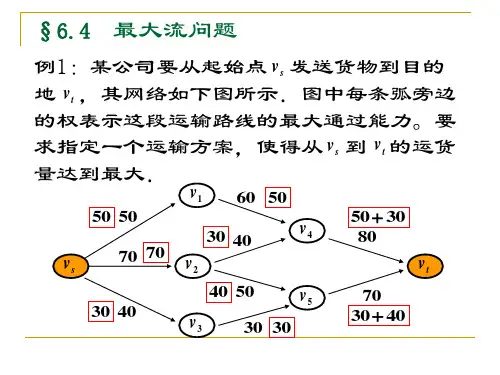
例题最大流的标号法精品文档例题最大流的标号法例2用标号法求下图所示的公路交通网络的最大流量 (要求写出标号过程并说明得到的的确是最大流)，其中，弧旁的数字是(c「f Q。

.⑴首先,给V s标上(0, )(2)检查V s，给V s为起点的未饱和弧的未标号的终点V2标号(V s, l(V2)),其中l(V2)min [l(V s),C s2 f s2】min[ ,15 7] 8其它点不符合标号条件。

⑶检查V2，给V2为终点的非零流弧的未标号的起点V3标号(V2, |(V3)),其中l(V3)min[g), f32】min[ 8,4] 4其它点不符合标号条件。

(4)检查v3，给v3为起点的未饱和弧的未标号的终点v4、v6标号(V4, l (V4)) > ( v6,l(V6))其中，l(V4)min[?3)234 ￡34] min[4,5 4] 1l(V6)min [l(V3),C36 f36] min [4,5 1] 4其它点不符合标号条件。

⑸检查v6，给v6为起点的未饱和弧的未标号的终点v t标号(v t, l (v t))其中，l(V t) mi n[l(V6), C6t f&] mi n[4,10 5] 4其它点不符合标号条件。

由于V t已标号，反向搜索可得增广链{(V s,V2),(V3,V2),(V3,V6),(V6,Vj}，在该增广链的前相弧(v s, v2), (v3, v6), (v6,v t)上增加l (v t) 4，在后向弧(v3, v2)上减去精品文档l(V t) 4，其它弧上的流量不变，则可得一流量v(f ) 20的新的可行流如下图重新开始标号：⑹首先,给V s标上(0, )(7)检查V s，给V s为起点的未饱和弧的未标号的终点V2标号(V s, l(V2)),其中l(V2) min [l(V s),C s2 f s2】 min[ ,15 11] 4其它点不符合标号条件。

例：在下面的有向图中1是发点， 6是收点，求最大流.
2 1 4
4 2
定理2. 容量网络的最大流不大于任一割集的割集容量.
(最大流--最小割)定理3. 容量网络的最大流等于最小割的割集容量.
证明：设f*是一个最大流，流量为F, 定义顶点集V的子集S*如下：
发点属于S*；若i点属于S*, 且弧(i,j)是非饱和弧，则j点属于S*；
若j点属于S*, 且弧(i,j)是非零流弧，则i点属于S*.
1 2 4 2 6
5 6
3 3 5
定义7： 设容量网络G=(V,A,c)的顶点集V是两个不交的部分S, S'的併集, 使得发点在S中，收点在S'中. 若A'是A的最小的子集，使得G中去掉A'后成为两个不相交的子图G1(S,A1)，G2(S',A2), 分别以S, S'为顶点集，则称A'是关于(S,S')的割集，记为A'=(S,S'). 割集A'中所有始点在S，终点在S'的弧的容量之和称为割集(S,S')的割集容量，记为C(S,S'). 对于不同的S和S'就有不同的割集，其中割集容量最小的割集称为容量网络G的最小割集(简称最小割). 易知：
(3) 若收点n没有被标号，对i点的标记中+，- 号加圈，表示i点已检查。转(2). 否则令j=n. 进入以下调整过程
(4) 若j点的标记为正, 即(i,+ ,d(j)), 令fij=fij+d(n), 否则fji=fji-d(n)
(5) 若j=1, 去掉全部标记, 转(1), 否则转(4).
1. 每条前向弧是非饱和弧，2. 每条后向弧是非零流弧.

(2,6) v1
v2
(0,10)
(0,3)
(0,3)
(6,6)
v0
(2,2)
v5
(0,4)
vn
(2,5)
(0,3)
(0,3)
(0,10)
v3
(0,4)
v4
(0,5)
(4,5)
(2,6) v1
v2
(0,10)
(0,3)
(0,3)
(6,6)
v0
(2,2)
v5
(0,4)
vn
(2,5)
(0,3)
(0,3)
(4,5)
(6,6) v1
v2
(4,10)
(0,3)
(0,3)
(6,6)
v0
(2,2)
v5
(4,4)
vn
(2,5)
(0,3)
(0,3)
(4,10)
v3
(0,4)
v4
(0,5)
(4,5)
(6,6) v1
v2
(4,10)
(0,3)
(0,3)
(6,6)
v0
(2,2)
v5
(4,4)
vn
(2,5)
(0,3)
再检查vi，直到vs为止
min1,2
1 min cij fij 对于增广链上的前向弧
2 min fij 对于增广链上的后向弧
(2)以为调整量进行调整
fij
'
ffiijj
(vi , vj ) (vi , vj )
fij (vi , v j )
去掉所有点的标号，对新的可行流f ' {fij '}进行标号
v2

（ ）如果终点 得到标号 ， ３ 则标号结束。
Ｓｅ２寻找增广链 。 ｔ ｐ
如果 同时存在几个始点或者几个 终点 ， 通过增加 虚 （） ２ 网络是流有方 向的容量网络 ； （ ） 网络 中每 条弧 都有 一个权 ， 表示允 许 网 ３在 它
拟 节点使得 网络 只有一个起点和一个终点 ；
一
种新的求解网络最大 流问题 的方法 ， 每个顶 点进 对
行标号 ， 顶点有几个 入弧 ， 即有几 个标号 ， 每次在选 择
・
１４・ １
计算机技 术与发展
第 ２ 卷 １
路径时先选取只有一个标 号 的路 径 ， 当所 有单标 号 的 路径走完时 ， 再按照弧容量较 大 ， 且最短 的路径选择增
Ａｂ ｔ ａ ｔ Ｉ ｐ ｏ ｉ ｅ ｅ ｗａ －ｌｂ ｌ ｇ ａ ｇ ｒ ｈ ｔ ｏ ｖ ｅｗｏ ｋ ｆ ｗ． ｅｙ ｖ Ｒｅ ｓｌｂ ｌｄ ａ ｄ ｖ ｒｅ ａ ｅ ｓ ｍｅ ｎ ｍｂ ｒｉ ｒ ｓ ｒ ｃ ：ｔ ｒ ｖｄ ｓ ａ ｎ ｗ ｙ ａ ｅ ｉ ｏ ｔ ｍ ｏ ｓ ｌ ｅ ｎ ｔ ｒ ｏ Ｅｖ ｒ ｅ ｘ ｉ ａ ｅ ｎ ｅ ｔｘ ｈ ｔ ａ ｕ ｅ ａ ｃ ｎ ｌ ｉ ｌ ｅ ｓ ｈ ｎ ｓ ｇａｅ． ｏ ｓ ｌ ａ ｒ ｄ ｓ Ｃｈ ｏ ｅｔ ｅ ｗａ ｔ ａ ａ ｒ ｄ ． ｔｒｅ ｅ ｗａ ｈ ａ ｎ ｙ ａｇ ａ ｅ。 ｈ ｓ ｔ ｅｗａ ｔ ａ ａ ｉ ｇ ｒ ａｃ ｃ ｐ ｃ ｔ ｎ ｈ ｒｅ ｉ ｙ ｈ ｔｈ ｓ ａ ｇ ａ ｅ Ａｆｅ ｖ ｒ ｙ ｙｔ ａ ｈ ｓ ｏ ｌ ｒ ｄ ｃ ｏ ｅ ｈ ｔ ｙ ｈ ｔｈ ｓｂ ｇ ｅ ｒ ａ ａ ｉｙ ａ ｄ ｓ ｏ ｔｒ
Ｏ 引 言
在现实生活 中 ， 在着 大量 的“ ” 问题 ， 存 流 的 计算 机技术和 网络技术 的迅速发展使得 网络最大流 问题在

最大流问题标号法例题详解最大流问题标号法例题详解本文以一道标号法求解最大流问题的例题胶加以详细讲解，帮助读者了解其原理及运算步骤。

题目如下：给定一个网络结构如下：s (源点) 0----1----2----3----4---- t (汇点)a 25 10 12 15 20其中 s 是源点，t是汇点，aij（i,j=0,1,2,3,4)是每条弧的容量，求整个网络的最大流量。

解：1、设置标号：在最大流问题中，为了求解最大流，最常用的方法是标号法。

首先，要设置各结点标号，因为本题中有5个结点，s源点的标号为0，t汇点标号为4，其他结点即1，2，3依次标号，标号的设定不仅便于求解，而且可以在初始化的时候使用。

2、初始化标号：初始化标号即将各结点初始化为两个空集合{}，即各结点的访问和未访问标号都是空集合，即无访问的结点标号为{}，访问过的结点标号也为{}。

3、依据标号法，从源点(s=0)计算，得出每条弧的剩余容量Cij，具体推导如下：源点0 1 2 3 41 0 25 10 12 152 0 0 10 7 103 0 0 0 8 104 0 0 0 0 20其中：Cij=aij-fij (i,j=0,1,2,3,4)其中，aij 为每条弧的容量，fij 为每条弧的流量，在初始情况下，fij=0，故Cij=aij。

4、找增广路径：从源点s开始，用深度优先搜索法查找从s到t的增广路径，具体步骤如下：设置一个数组P[i]用以记录路径，P[i]表示从s到i节点所经过的上一个结点，先从源点s开始，P[0]=-1，然后查找s出发可以到达的结点，若Cij>0，则有路可达，将P[j]=i（j为s出发可达的结点），接着查找j出发可以到达的结点（该结点未被访问过）若Cjk>0，则有路可达，把P[k]=j，以此类推，直到找到P[t]=-1，即从s到t 的一条增广路径找到，这条增广路径的路径上的容量称为Cmin，它是该增广路径上各结点之间的容量最小值。

三、最大流问题的标号法

步骤： 判断是否存在增广链, 并设法把增广链找出来, 并予以调整, 最终使图中无增广链.
此算法从网络中的一个可行流f 出发（如果D中 没有
f，可以令f 是零流），运用标号法，经过标号过程和
调整过程，最终可以得到网络中的一个最大流。
1． 标号过程 在标号过程中，网络中的点分为两种： 已标号的点（分为已检查和未检查）和未标号的点。 每个标号点的标号包含两部分： 第一个标号表示这个标号是从那一点得到的， 以便找出增广链。 第二个标号是从上一个标号点到这个标号点的流量的 最大允许调整值， 是为了用来确定增广链上的调整量θ。
运输网络最大流问题
一、引言
1.应用背景 在许多实际的网络系统中都存在着流量和最大流问 题。 例如铁路运输系统中的车辆流，城市给排水系统的 水流问题,控制系统中的信息流问题，常见的人流， 物流，水流，气流，电流，现金流等。 在一定条件下,求解给定系统的最大流量,就是网络最大 流问题.

2.问题描述
标号过程开始，先给vs 标号（0，+∞）。 这时，vs 是标号未检查的点，其它都是未标号点。 如果vt有了标号，表示存在一条关于f 的增广链。 如果标号过程无法进行下去，并且vt未被标号， 则表示不存在关于f 的增广链。 此时，就得到了网络中的一个最大流。
例 求图10-25的网络最大流，弧旁的权数 表示（cij , fij）。
(4 , 3)
(1 , 1)
v2
v4
(3 , 3)
(5 , 3) (3 , 0) (2 , 1)
(0,+)
vs
(5 , 1)
(1 , 1)
(2 , 2)
vt

clc,clear u=[0 5 4 3 0 0 0 0; 0 0 0 0 5 3 0 0; 0 0 0 0 0 3 2 0; 0 0 0 0 0 0 2 0; 0 0 0 0 0 0 0 4; 0 0 0 0 0 0 0 3; 0 0 0 0 0 0 0 5; 0 0 0 0 0 0 0 0]; n=length(u); f=zeros(n,n); list=[];maxf(n)=1; while maxf(n)>0 maxf=zeros(1,n);pred=zeros(1,n); list=1;record=list;maxf(1)=inf; %list 是未检查邻接点的标号点，record 是已标号点 while (~isempty(list))&(maxf(n)==0) flag=list(1);list(1)=[]; label1= find(u(flag,:)-f(flag,:)); label1=setdiff(label1,record); list=union(list,label1);
(2,7 )
v5
b=[0 10 6 3 0 0; 0 0 4 0 0 3; 0 0 0 0 12 4; 0 0 5 0 2 0; 0 0 0 0 0 5; 0 0 0 0 0 0]; c=[0 12 7 8 0 0; 0 0 8 0 0 5; 0 0 0 0 10 7; 0 0 9 0 7 0; 0 0 0 0 0 8; 0 0 0 0 0 0]; [f wf zwf]=BGf(c,b)
c= 10 从两种方法得到的最小生成树不同，但权和都为 10.
实 验 体 会
在最优化上机实验中，将数学语言转化成了计算机语言，通过学习 Ford-Fulkerson 算法， 我掌握了更加高效的解决最大流和最小费用最大流问题。 通过学习编程代码，我学习了最大流的算法，同一个连通图的最大流是唯一的。 通过学习，提高了编程水平。

第七章Operational厂§ 4网络最大流问题网络最大流冋题是网络的另一个基本冋题。

许多系统包含了流量问题。

例如交通系统有车流量，金融系统有现金流，控制系统有信息流等。

许多流问题主要是确定这类系统网络所能承受的最大流量以及如何达到这个最大流量。

4.1基本概念与定理1. 1.网络与流定义14 （1）网络：例1如图7-20是连结某产品产地’和销地一的交通图。

弧:1 表示从二到匚的运输线，弧旁的数字表示这条运输线的最大通过能力，.，括号内的数字表示该弧上的实际流一［。

现要求制定一个运输方案，使从一运到尸，的产品数量最多。

可行流与最大流输网络的实际问题中，我们可以看出，对于流有两个基本要求：一是每条弧上的流量必须是非负的且不能超过该弧的最大通过能力(即该弧的容量)二是起点发出的流的总和(称为流量)，必须等于终点接收的流的总和，且各中间点流 入的流量之和必须等于从该点流出的流量之和， 即流入的流量之和与流出的流量之和的差为 零，也就是说各中间点只起转运作用，它既不产出新的物资，也不得截留过境的物资。

因此有下面所谓的可行流的定义。

定义14对于给定的网络 D=(V,A,C )和给定的流 』」：.「，若「满足下 列条件:(1)容量限制条件：对每一条弧 .-，有- -(7.9)(2)平衡条件： 对于中间点：流出量=流入量，即对于每一个对于出发带点T ：，有SA -'K/)对于收点①，有 工二 'I(7.12)则称/ - ■为一个可行流，•-称为这个可行流的 流量。

注意，我们这里所说的出发点 r 是指只有从匚发出去的弧，而没有指向J 的弧;收点二是指只有弧指向--，而没有从它的发出去的弧。

在运i (i 丰 s,t)，有(7.10)(7.11)可行流总是存在的。

例如令所有弧上的流，就得到一个可行流，（称为零流）,其流量 ': 一。

如图7-20中，每条弧上括号内的数字给出的就是一个可行流 3 - f/yJ ，它显然满足定义中的条件（1 ）和（2）。

最⼤流问题的⼏种经典解法综述⼀、什么是最⼤流问题假设现在有⼀个地下⽔管道⽹络，有m根管道，n个管道交叉点，现在⾃来⽔⼚位于其中⼀个点，向⽹络中输⽔，隔壁⽼王在另外⼀个点接⽔，已知由于管道修建的年代不同，有的管道能承受的⽔流量较⼤，有的较⼩，现在求在⾃来⽔⼚输⼊的⽔不限的情况下，隔壁⽼王能接到的⽔的最⼤值？为解决该问题，可以将输⽔⽹络抽象成⼀个联通的有向图，每根管道是⼀条边，交叉点为⼀个结点，从u流向v的管道能承受的最⼤流量称为容量，设为cap[u][v]，⽽该管道实际流过的流量设为flow[u][v]，⾃来⽔⼚称为源点s，隔壁⽼王家称为汇点t，则该问题求的是最终流⼊汇点的总流量flow的最⼤值。

⼆、思路分析关于最⼤流问题的解法⼤致分为两类：增⼴路算法和预流推进算法。

增⼴路算法的特点是代码量⼩，适⽤范围⼴，因此⼴受欢迎；⽽预流推进算法代码量⽐较⼤，经常达到200+⾏，但运⾏效率略⾼，如果腹⿊的出题⼈要卡掉⼤多数⼈的code，那么预流推进则成为唯⼀的选择。

( ⊙ o ⊙ )咳咳。

先来看下增⼴路算法：为了便于理解，先引⼊⼀个引理：最⼤流最⼩割定理。

在⼀个连通图中，如果删掉若⼲条边，使图不联通，则称这些边为此图的⼀个割集。

在这些割集中流量和最⼩的⼀个称为最⼩割。

最⼤流最⼩割定理：⼀个图的最⼤流等于最⼩割。

⼤开脑洞⼀下，发现此结论显⽽易见，故略去证明（其实严格的证明反⽽不太好写，但是很容易看出结论是对的，是吧）。

这便是增⼴路算法的理论基础。

在图上从s到t引⼀条路径，给路径输⼊流flow，如果此flow使得该路径上某条边容量饱和，则称此路径为⼀条增⼴路。

增⼴路算法的基本思路是在图中不断找增⼴路并累加在flow中，直到找不到增⼴路为⽌，此时的flow即是最⼤流。

可以看出，此算法其实就是在构造最⼩割。

增⼴路算法⽽预流推进算法的思路⽐较奇葩（没找到⽐较好的图，只能⾃⾏脑补⼀下了。

= =#）：先将s相连的边流⾄饱和，这种边饱和的结点称为活动点，将这些活动点加⼊队列，每次从中取出⼀个点u,如果存在⼀个相邻点v是⾮活动点，则顺着边u->v 推流，直到u变为⾮活动点。

f
ij

• 最大流问题是一个特殊的线性规划问题。即求一组 ｛fij｝，在满足条件①和②下使v(f)达到极大。将会看 到利用图的特点，解决这个问题的方法较之线性规划 的一般方法要方便、直观得多。
增广网络
作出一个和原网络G具有相同顶点并具有相同发点和收点的增 广网络G’，G’包含两类边，对G中每一条边(i,j): 1.若fij<cij ,作正向边(i,j)，规定容量c’ij=cij –fij，即剩余容量。(正 规边) 2.若fij>0,作反向边(j,i), 规定容量c’ ji= fji， c’ ji事实上是边(j,i),上最 多可以减少的容量.(增广边) 如果增广网络上存在着由s到t的通路P(称为原网络的一条增广 路)
思考题
• 四个人：张三、李四、王五、赵六，四种乐器： 小提琴、大提琴、钢琴、吉他。 • 已知四人的擅长如下： • 张三擅长拉大提琴和弹钢琴； • 李四擅长拉小提琴、大提琴和吉他； • 王五擅长拉小提琴、大提琴； • 赵六只会弹吉他。 • 今假设四人同同台演出，每人各奏一种乐器，问 四人同时各演奏一种乐器时所有可能的方案，试 把此问题化为最大流问题。
量多的人能就业。 其中 x1 ,, x5 表示工人。
y1 ,, y5 表示工作。
x1
y1 y2
x2
x3
x4
y3
y4
x5
y5
x1
y1 y2
x2
vs
x3
x4
y3
y4
vt
x5
y5
二部图中最大匹配问题，可以转化为最大流问题求解。在 二部图中增加两个新点 vs , vt 分别作为发点，收点。并用 有向边把它们与原二部图中顶点相连，令全部边上的容量 均为1。当网络流达到最大时，如果 ( xi , y j ) 上的流量为1，

N
JU
ST
-Z
H
A N
G
vs
vt
基本定理(可行流与割集的关系)
流量为W ( f ), (V1 ,V1 )是分离vs , vt的任一割集，割集容量为C(V1 , V1 )
分离v s , v t 的最小割的容量
可行流 f 是最大流 不存在从 v s 到 v t 的可增广链
N
JU
ST
任一个网络 G中， 从v s到v t 的最大流的流量
A N
设 f { fij }是网络D=（V，A，C）的一个可行流
G
弧关于流的分类
4、如果fijБайду номын сангаас0，该弧是非0弧；
N
JU
v1
cij=5 fij>0
ST
v2
v1
cij=5 fij=0
-Z
v2
H
3、如果fij=0，该弧是0流弧；
（v1，v2）是0流弧
（v1，v2）是非0弧
A N
设 f { fij }是网络D=（V，A，C）的一个可行流
ST
vt 。而 v1 对 v5 来讲是流 d) 检查与v5 相邻接且未标号的点 v1 ， 入，现欲增加流出量，应该压缩 v1 的流入量，只要的流入 量 f 15 0, 可令调整量为
JU
8(8)
v3
6(1)
5(5)V1
N
割集 {(v1 , v3 ), (v2 , v4 )}
vs
7(5)
2(0)
vt
10(8)
割集的容量为9+9=18
v2
K
9(9)
v4
考虑KK的不同画法
8(8)

武
10
28
10 8
广
6
沈
京
18
发点vs =成都，收点vt =北京。前面已订购机票情况表中的数字即是 各边上的容量（允许通过的最大旅客量），当各边上的实际客流量为
零时略去不写，以零流作为初始可行流。
利用标号法（经5次迭代）可以得到从成都发送旅 客到北京的最大流量如图所示
0
西
6
郑
重
10 0 6
0
0
2
10 10
标号过程: (1)给vs标号(-,+∞)，vs成为已标号未检查的点，其 余都是未标号点。
(2)取一个已标号未检查的点vi，对一切未标号点vj： 若有非饱和弧(vi,vj)，则vj标号(vi,l(vj))，其中l(vj)＝ min[l(vi),cij – fij]，vj成为已标号未检查的点；若有非 零弧(vj,vi)，则vj标号(-vi,l(vj))，其中l(vj)＝min[l(vi), fji]， vj成为已标号未检查的点。vi成为已标号已检查的点。
[-,+∞]
vs
x[v1 s,1] [xv2s,1] [xv3s,1] [xv4s,1]
x[v5 s,1]
[x1,1y1] [x1,1y]2 [x1,1]y3
y4
y5
[y1,1]vs
1
[v-,s+∞]
x1
1
x[2vs,1]
[xv3 s,1] x4 [vs,1] x5 [vs,1]
[x2,1y]1 1
(3,0) vt (2,1)
v1 (2,2)
v3
(vs,4)
(-v2,1)
(3,3) v2 (4,3)
(-,+∞)

取 min ij ，显然 0。 f 1 ： • 我们把 f 修改为 f ij vi , v j 为 上前向边 f1 f ij vi , v j 为 后向边 f ij 其余 f1仍为可行流（即满足容量限制条件与 • 不难验证 平衡条件），但是 f1的总流量等于 f 的流加 ， 这与 f 为最大流矛盾，所以 vt不属于 S 。
• 检查与 v5 点邻接的未标号点有 v1 , vt，发现 v1 , 点满足 v1 , v5 E且 f15 3 0 ，令 v1 min 3, 2 2, 则给 v1点以标号 v5 , 2 。 , • v4 点未标号，与 v1邻接，边 v1 , v4 E且 f14 2 c14 5,所以令 v 4 min 3, 2 2, 给 v4 以标 号 v1, 2 。 • vt 类似前面的步骤，可由 v4得到标号 v4 , 2。 • 由于 vt 已得到标号，说明存在增广链，所 以标号过程结束，见图5-44。
• 但流量W又满足
W
cij fij 0
vi S , v j S
v j S , vi S
vi S ,v j S

fij f Ji
vi S ,v j S

cij
• 所以最大流的流量等于最小割的容量，定理得到 证明。 • 定义22 容量网络G，若 为网络中从vS到 vt的一 条链，给 定向为从vS到 vt, 上的边凡与 同向称 为前向边，凡与 反向称为后向边，其集合分别 用和 表示，f是一个可行流，如果满足
（3）重复（2）直到收点 vt 被标号或不再有顶点 可标号时为止。 • 如若 vt 得到标号，说明存在一条可增广链，转 （第2步）调整过程。若 vt 未获得标号，标号过 程已无法进行时，说明f已是最大流。 2. 调整过程 f ji 若 vi , v j 是可增广链上的前向边 f ji 若 v , v 是可增广链上的后向边 （1）令 fij i j 若 vi , v j 不存在可增广链上 f ji （2）去掉所有标号，回到第1步，对可行流 f 重 新标号。