高一数学 正弦函数图像

第二课时
高一
数学
画出函数y=sinx，x∈R的图象
y 1 -6π -4π -5π -3π -1 -2π -π
O
π 2π
3π 4π
5π 6π x
这节课我们研究函数y=cosx，x∈R的图象
高一 数学
1．知道余弦函数图象的大致形状
2．会利用“五点法数的图象
-1
高一
数学
例1 用“五点法”画出下列函数的简图：
(1)y=cosx-1，x∈[0，2π ]； (2)y=-cosx，x∈[0，2π ] .
高一
数学
思考7：
1、函数y=cosx-1的图象与函数y=cosx的图象有什么关系？ 2、函数y=-cosx的图象与函数y=cosx的图象有什么关系？
高一
数学
关键作用的点有哪几个？
y
1 O -1
高一 数学
2
π
2
2π
x
思考6：函数y=cosx，x∈R的图象叫做余弦曲线，怎样画
出余弦曲线，余弦曲线的分布有什么特点？ y
2
2
2 2
1 2
2
2
2
2
2
x
2
2
O
1 π
3p 2
y 1
O π 2π x 2 2 1 1 2.作与正、余弦函数有关的函数图象，是解题的基
O
p 2
2 π x
本要求，用“五点法”作图是常用的方法.
高一 数学
课后作业 P34 练习 1,2题
高一
数学
思考1：观察函数y=x2与y=(x＋1)2 的图象，你能发现这 两个函数的图象有什么内在联系吗？ y

【答案】 B
3．点
M
π，－m 2
在函数
y＝sin
x
的图象上，则
m
等于(
)
A．0
B．1
C．－1
D．2
【解析】 由题意－m＝sin π2，∴－m＝1，∴m＝－1.
【答案】 C
4．函数 y＝cos x 与函数 y＝－cos x 的图象( )
A．关于直线 x＝1 对称
B．关于原点对称
C．关于 x 轴对称
1.正、余弦函数的图象每相隔2π个单位重复出现，因此，只要记住 它们在[0，2π]内的图象形态，就可以画出正弦曲线和余弦曲线.
2.作与正、余弦函数有关的函数图象，是解题的基本要求，用“五 点法”作图是常用的方法.
y
1
x
o1
o
632
2 5
7
4
3 5 11 2
36
6
3
23
6
-1
让单位圆继续逆时针旋转一周，函数值会重复出现，再继续逆时针旋转一周， 函数值又重复出现；相反地，让单位圆顺时针旋转一周，函数值也会重复出 现，再继续顺时针旋转一周，函数值又重复出现.
由诱导公式一知：函数y = sinx在[2kπ，2(k+1)π](k∈z，k≠0)上的图象 与y = sinx在[0，2π]上的图象完成一致.因此，将函数y = sinx在[0，2π]上 的图象不断向左、向右平移（每次运移动2π个单位），就可以得到正弦 函数y = sinx在R上的图象.
-1
描点连线，如图
思考：你能利用函数y＝sin x，x∈[0，2π]的图象，通过图象 变换得到y＝1＋sin x，x∈[0，2π]的图象吗？同样地，利用函 数y＝cosx，x∈[0，2π] 图象，通过怎样的图象变换就能得到 函数y＝-cosx，x∈[0，2π] 的图象？

六、例 题 讲 解
例1：用五点法画出函数的简图 y=1+sinx, x∈[0，2π] ： ∈ ，
分析：利用五点法画正弦函数y=sinx的图像 分析：利用五点法画正弦函数 的图像 π π ) π ， 五个关键点是： 五个关键点是：(0,0) ( 2 ,1) (π,0) (32 ,−1 (2π,0)， π
二.正弦函数的图像 正弦函数的图像
在画正弦函数图像时,我们可以先画 在画正弦函数图像时,我们可以先画 上的正弦函数的图像,再利 出[ 0, 2π ] , 上的正弦函数的图像 再利 用周期性将其延拓到整个定义域上. 用周期性将其延拓到整个定义域上
正弦函数的图象
用描点法作出函数图象的主要步骤是怎样的？ 描点法作出函数图象的主要步骤是怎样的？
练习: 练习: 用单位圆中正弦线表示正弦的方法 π π 作出点 ( ， ) sin 3 3
y
P
( ,sin ) 3 3
A O
π
π
O1 M
π 6
π 2
π
X
仿上例可以作出 y=sinx , 2π]的图象 x∈[0, 2π]的图象
四、几何法作图
用正弦线作正弦函数 用正弦线作正弦函数 的图象
y = sin x( x ∈[0,2π ])
π
2
2
,1 )
最低点： 最低点： (3π ,−1 ) 轴的交点： 与x轴的交点： (0, 0) 轴的交点
(π , 0) (2π ,0)
在精度要求不高的情况下，我们可以利用这 个点画出函数 在精度要求不高的情况下，我们可以利用这5个点画出函数 的简图，一般把这种画图方法叫“五点法画图” 的简图，一般把这种画图方法叫“五点法画图”。
回忆单位圆中正 弦函数的定义

1
3 5

2
2 3
2

2
O
1

2

3
2
2
5
2
3
x
函数
y＝sin x(x∈R)
y＝cos x (x∈R)
图像
·
最
值
·
周期
T=2
奇偶性
对称轴
对称中心
增区间
减区间
最值
=
奇函数
π
2
+ , ∈ Z
(, 0) ∈ Z
π
π
[− + 2, + 2], ∈ Z
典 型 例 题 1
正弦、余弦（型）函数的单调性
例1 (1)函数 = (2
(2)函数 = (2
(3)函数 =

(
6

− )的单调递减区间为___________________
6

− )， ∈ [0,2]的单调递减区间为_____
6
− 2)的单调递增区间为___________________
跟 踪 训 练 1
正弦、余弦（型）函数的单调性
(1)函数 = 2(

− )，
3
∈ [−, 0]的单调递增区间是(
5
A.[−, − ]
6
5

B.[− , − ]
6
6

C.[− , 0]
3

D.[− , 0]
6
(2)函数 =

3(
3
− 2)的单调递减区间为_________________
(1) 函数() = (2 − Nhomakorabea)，

y
2
1
0
π
2π
3π
4π x
-1
ω的作用：使正弦函数的周期发生变化。
你能得到y=sin （ x)与y=sinx 图象的关系吗？
函数 y sin(x) 的图象，可以看作
是把 y sin( x) 的图象上所有点的横坐
标* 1 倍（纵坐标不变）而得到的. 0
T 2
练习：求下列函数的最大值、最小值、 周期
先观察y=2sinx、y= 1 sinx与y=sinx的图象间的关系
y
2
2
1
0
π
2π x
-1
-2
你能得到y=Asinx与y=sinx 图象的关系吗？
1.y=Asinx（A>0)的图象是由y=sinx的图象上所 有点的横坐标不变，纵坐标*A倍而成. 2.值域 [ -A, A]最大值A,最小值-A
正弦型函数y =Asin(ωx + )的图象
5、 3 2
1
5
y sin( x ) 1
2 2
ymax 2
ymin
2
T 2
正弦型函数y =Asin(ωx + )的图象和性质
3、 的作用：研究 y=sin(x+ )与y=sinx 图象的关系
先观察y = sin（x+ ）、y = sin（x － ）
2
2
与 y=sinx 的图象间的关系
y
2
1
0
π
2π
3π
4π x
-1
作y=sin
1 2
x的图象
1x
0
2
x
0
sin 12x 0
1、列表

在电路分析中，正弦交流电和余弦交流电可以叠加形成复杂 的交流电信号。同时，在振动和波动问题中，正弦波和余弦 波也可以叠加形成复杂的波形。
CHAPTER 05
图形变换及应用
平移变换
平移变换定义
将函数的图象在直角坐标系中沿x轴或y轴方向移动一定的距离，得到新的函数图象。
正弦函数、余弦函数的平移变换规律
过程与方法
通过观察和实验，理解正 弦函数、余弦函数的图象 形状和变化规律，培养数 形结合的思想方法。
情感态度与价值观
感受数学与生活的联系， 体会数学的应用价值，培 养学习数学的兴趣和热情 。
教学内容
正弦函数、余弦函数 的定义域、值域、周 期性等基本性质。
利用正弦函数、余弦 函数的图象解决简单 的实际问题。
对称变换
对称变换定义
将函数的图象在直角坐标系中关于某条直线或某个点进行对称，得到新的函数图象。
正弦函数、余弦函数的对称变换规律
正弦函数、余弦函数的图象关于原点对称，也关于直线x=kπ+π/2（k∈Z）对称。即 函数y=sin(x)或y=cos(x)的图象关于原点对称，得到y=-sin(x)或y=-cos(x)的图象；关
求函数的解析式； 求函数的递增区间；
求使$y leqslant 0$的$x$的取值范围。
例题一：利用正弦、余弦函数图象求解析式
解析
由题意知，函数的周期为$T = 4 times (frac{pi}{3} - frac{pi}{12}) = pi$，从而得到$omega = frac{2pi}{T} = 2$。
例题一：利用正弦、余弦函数图象求解析式
又因为函数的最大值为5，所以振幅 $A = 5$。
所以函数的解析式为$y = 5sin(2x frac{pi}{6})$。

2
-
4
-
6
-
x
因为终边相同的角的三角函数值相同，所以y=sinx的图象在……， 4 ,2 , 2 ,0, 0,2 , 2 ,4 , …与y=sinx,x∈[0,2π]的图象相同
-
二、余弦函数y=cosx的图象
y
余弦曲线
1




2 , 0)
3 ( , 0) 2
与x轴的交点： (
-
； / 五莲红
bgk839utb
那个送莫艳艳回家的男士不是别人，正是司空阳宇，即使时隔十年，她再一次正面碰见那个男子，她还是一眼就将他认了出来。 敲门声响起的时候她正在洗脸，一边喊了几句“来了、来了”一边快快的去开门。 莫艳艳正倚在那位长相看起来十分清秀的男士的身上，整个人都是一副娇弱无力的样子，孤独晓寂从来不曾如那样一刻、那般 的讨厌起那个看起来总是轻而易举的就能卖弄风骚的莫艳艳。她怔怔的看着那位男士，可惜那个男子并不认识她，只是礼貌的 开口“你是她室友吗，那现在麻烦你把她扶回去吧！”。 孤独晓寂不知道自己是如何接手莫艳艳的，她只觉得那样的莫艳艳让她觉得很厌恶，她从来没有过的一种厌恶。她一瞬不瞬的 看着司空阳宇的背影消失在楼道之后，便将莫艳艳扶回了家门，似丢垃圾般将她直接推向了就近的沙发。然后，把自己锁进房 中，心疼到不知所以的流下泪来，这世上、果然所有的男士都是喜欢莫艳艳那类的娇媚女人么？ 莫艳艳不耐烦的敲她的门“孤独晓寂，你给我出来，你在闹什么别扭，怎么总是那么自以为是，你为何不问问我、那个男人是 谁？” 孤独晓寂嫌烦的捂住了耳朵，她现在不想听到莫艳艳的声音，更不想看到那样的一个人！ 莫艳艳不死心的一遍遍的拍打她的房门，她还不信了，孤独晓寂烦不甚烦的时候终于开了门，莫艳艳一把将她拽了出来，她费 了很大的劲才将孤独晓寂拽了出来，她堵在孤独晓寂的门口，不屑的看了孤独晓寂一眼“至于吗你，我是跟他做了什么了吗？ 至于反应那么大吗？你不过是暗恋他十年而已，况且他又不认识你，我们、我们是实实在在的认识了二十多年的姐妹，姐妹， 知道吗” 孤独晓寂听她讲出这样的话，心里还是因为司空阳宇而难过到忍不住落下泪来，却不曾开口说出一个字。

马上就上课了，同学们准备好了吗？
满足 sin x 1 x的 x 的个数是多少
一、复习正弦线的概念 y
P
x
MO
正弦线： MP
二、在直角坐标系中如何作点（ ，sin ） 33
y
P MO
C(
3
,
sin
3
)
x
三、用几何方法作正弦函数 y sin x(x [0,2 ])
的图象
（1）作直角坐标系，在直角坐标系的y轴左侧画单位圆；
（2）把单位圆分成12等份。过单位圆上的各分点作x轴 的垂线，可以得到对应于各角的正弦线；
（3）找横坐标：把x轴上从０到2这一段分成12等份； （4）找纵坐标：将正弦线对应平移，即可指出相应12
个点； （5）连线：用平滑的曲线将12个点依次从左到右连接
起来，即得到 y sin x(x [0,2 ])的图象。
六、例题
例1、画出函数 y 1 sin x, x [0,2 ]的简图。
解：按五个关键点列表：
x
0
1 sin x 1
2
2
1
3 2
2
0
1
y
.2
1
.
.
.
.
o
2
x
画出下列函数的简图：
(1)y sin x, x [0,2 ] (2)y 2sin x, x [0,2 ]
解： x
0
2
3
2
2
sin x 0 -1 0 1 0
2sin x
0 2 0 -2 0
y y 2sin x, x[0,2]
2
y sin x, x[0,2]
1
o
2
x
八、小结：

•
•
•
•
之前有个网友说自己现在紧张得不得了 ，获得 了一个 大公司 的面试 机会， 很不想 失去这 个机会 ，一天 只吃一 顿饭在 恶补基 础知识 。不禁 要问， 之前做 什么去 了？机 会当真 就那么 少？在 我看来 到处都 是机会 ，关键 看你是 否能抓 住。运 气并非 偶然， 运气都 是留给 那些时 刻准备 着的人 的。只 有不断 的积累 知识， 不断的 进步。 当机会 真的到 来的时 候，一 把抓住 。相信 学习真 的可以 改变一 个人的 运气。
O MA x
三角函数
三角函数线
正弦函数 余弦函数 正切函数
sin=MP cos=OM
tan=AT
正弦线MP 余弦线OM 正切线AT
4.问题与思考
4.回顾三角函数的定义
三角函数
定义域
sin
cos
tan
R
R
{ | k , k Z}
2
值域
[-1,1] [-1,1] R
那我们是如何研究一个函数的？
•
•
学习重要还是人脉重要?现在是一 个双赢 的社会 ，你的 价值可 能更多 的决定 了你的 人脉， 我们所 要做的 可能更 多的是 专心打 造自己 ，把自 己打造 成一个 优秀的 人、有 用的人 、有价 值的人 ，当你 真正成 为一个 优秀有 价值的 人的时 候，你 会惊喜 地发现 搞笑人 脉会破 门而入 。从如 下方 面改进 ：1、专 心做可 以提升 自己的 事情； 2、学 习并拥 有更多 的技能 ；3、成 为一个 值得交 往的人 ；4学 会独善 其身， 尽量少 给周围 的人制 造麻烦 ，用你 的独立 赢得尊 重。
凡 事 都 是 多 棱 镜 ， 不 同 的 角度 会

上都单调递减，其值从1减小到-1.
最大值与最小值
【整理】从上述对正弦函数、余弦函数的单调性的讨论中容易得到：

+ ( ∈ ) 时取得最大值1，


当且仅当 = − + ( ∈ ) 时取得最小值-1；

①正弦函数当且仅当 =
②余弦函数当且仅当 = ( ∈ ) 时取得最大值1，
【1】周期性：观察正弦函数的图像，可以发现，在图像上，横坐标每隔2π个单位
长度，就会出现纵坐标相同的点，这就是正弦函数值具有的“周而复始”的
变化规律.实际上，这一点既可以从定义中看出，也能从诱导公式中得到反映.即自
变量 的值加上2π的整数倍时所对应的函数值，与 所对应的函数值相等.数学
上用周期性来定量地刻画这种“周而复始”的规律.
如何用自变量的系数表示上述函数的周期呢？
事实上，令 = + ，那么由 ∈ 得 ∈ ，且函数 = , ∈ 及函数
= , ∈ 的周期都是.
因为 + = + + = +




+ ，所以自变量增加 ，函数值




+ ,
+ ( ∈ ) 上都单调递减，其值从1减小到-1.


单调性


−
−



−



同样的道理结合余弦函数的周期性我们可以知道：
余弦函数在每一个闭区间
在每一个闭区间
− + , ( ∈ ) 上都单调递增，其值从-1增大到1；
, + ( ∈ )
关于y轴对称.所以正弦函数是奇函数，余弦函数是偶函数.

y=sinx
1
9 2
7 2
5 2
3 2
2
o
-1
2 3
4 x
正弦曲线
-2
-
余弦曲线
-2
-
y y sinx , x R
1
x
o
2 3
4
-1 y1
定义域：R
y cosx , x R 值域：[-1,1]
o
2
3
x
-1
思考：在确定正弦函数的图象形状时，应该抓住哪些关键点？
y
1
o
2
3 2
2 x
-1
五个关键点:
3 5 11 2
6
3
2
36
6
3
2
3
6
-1
y
1
x
o1
o
632
2 5 36
7 4 3 5 11 2
6
3
23
6
-1
y
1
x
o1
o
632
2 5 36
7 4 3 5 11 2
6
3
23
6
-1
思考:如何画函数y =sinx(x∈R)的图象?
sin(x+2k)=sinx, kZ
y=sinx， x[0,2]
2
1 画出 y＝sin x 的图象和直线 y＝ .
2
1
1
可知 sin x≥ 的解集为 y＝sin x 图象与直线 y＝ 的交点及上方部分的集合，即
2
2
π
5π
函数定义域为{x| ＋2kπ≤x≤ ＋2kπ，k∈Z}．
6
6
02

问题 正切函数 y = tanx 是否为周期函数？
∵f x +π = tan x +π = tanx ＝f(x)
是它的一个周期 ∴y = tanx 是周期函数，
ππ (- , ) 2 2
想一想：先作哪个区间上的图象好呢？ 一个周期内的图像
y tan x x 利用正切线画出函数 ， ， 的图像: 2 2 把单位圆右半圆分成8等份。 作法: (1) 等分： 3 3 (2) 作正切线 ， ， ， ， ， 8 8 4 8 8 4 (3) 平移 (4) 连线

自我小结
谈谈本节课你的收获是什么？ 哪部分知识掌握的比较好？ 还有什么不清楚的细节吗？……… 1.课本习题 2.学案课后练习 3.（选做）导学练
思考
我们已经学习了正弦、余弦函数的图像 我们是怎么得到它们的图像的呢？ 利用单位圆中的三角函数线作图 （由一个周期到整个定义域）
探索新知
通过回顾，对我们研究正切函数图像有 什么启发吗？ （利用正切线）
π 2 3π 2
O
π
2π x
-1
y cosx , x [0,2π]
正弦、余弦函数的图象
y
1 -4 -3 -2 -
o
-1

2
3
4
5
6
x
正弦函数的图象 y=cosx=sin(x+ ), xR
2

正弦曲 线
形状完全一样 只是位置不同
余弦函数的图象
y
1
余弦曲 线

-4
-3
-2
其值从-1增至1 其值从 1减至-1
y=cosx (xR)
6
4

1
1－ cos x 的图象，如图所示.
3
训练3
方程sin x＝lg x的实根个数有
A.1个
B.2个
C.3个
√
D.无穷多个
在同一直角坐标系中作函数y＝sin x与y＝lg x的图象.
由图中可以看出两函数图象有三个交点(xi，yi)，其中xi∈(1，10)(i＝1，2，3)
是方程sin x＝lg x的解.
y
1
-4
-3
-2
-
o

-1
2
3
4
5
6
= , ∈

左移

y
x

= = +
, ∈

1
-4
-3
-2
-
o
-1

2
3
4
5
6
x
余弦函数的图象 = , ∈
余弦函数 = , ∈ 的图像叫余弦曲线，是和
弦函数值0 ，并准确找到点(0 , 0 )的位
置呢？
探究新知（一）：正弦函数的图象 = , ∈
探究新知（一）：正弦函数的图象 = , ∈
问 题 4 ：你会选 , 上的哪些 0 来画正弦函数的图像？
结论： 在 , 内取等分的点，最简便准确
这些点用光滑的曲线连接起来，得到比较精确的函数
= , ∈ , 的图像
函数 = , ∈ , 的图像
探究新知（一）：正弦函数的图象 = , ∈
问 题 5 ：根据函数 = , ∈ , 的图像，你能想
象正弦函数 = , ∈ 的图像吗？依据是
什么？请画出该图像
y

与三角函数有关的函数定义域问题常常归结为解三角不等式 (组)问题，利用三角函数的图像或单位圆中的三角函数线直观地求 出解集．
跟踪训练 2 求下列函数的定义域： (1)y＝ sinx； (2)y＝lg(sinx)＋ 9－x2.
解析：(1)由 sinx≥0， 得函数的定义域为{x|2kπ≤x≤2kπ＋π，k∈Z}． (2)由题意，得s9i－nxx>20≥0. 解得－2kπ3<≤x<x≤2k3π，＋πk∈Z 所以 0<x≤3. 故函数的定义域为(0,3]．
【解析】 原函数的定义域为 R，关于原点对称． 又 f(x)＝xsin(π＋x)＝－xsinx， f(－x)＝－(－x)sin(－x)＝－xsinx＝f(x)， 因此函数 f(x)＝xsin(π＋x)为偶函数． 【答案】 B
方法归纳
判断函数奇偶性的步骤：(1)判断函数的定义域是否关于原点对 称；(2)判断 f(x)与 f(－x)之间的关系．
类型五 正弦函数的单调性
[例 5] 求函数 y＝log 1 (sinx)的递增区间．
2
【思路点拨】 设 u＝sinx，先由 sinx>0，得出相应的 x 的取值
范围，再利用 y＝log 1 u 的单调性求解．
2
【解】 设 u＝sinx，由 sinx>0，
得 2kπ<x<2kπ＋π(k∈Z)．
因为12<1，
跟踪训练 3 (2016·马鞍山期中)y＝sinx－|sinx|的值域是( ) A．[－1,0] B．[0,1] C．[－1,1] D．[－2,0]
解析：y＝20s，in0x≤，s－in1x≤≤s1inx<0， 因此函数的值域为[－2,0]．故选 D. 答案：D
类型四 正弦函数的奇偶性 [例 4] 函数 f(x)＝xsin(π＋x)在其定义域上是( ) A．奇函数 B．偶函数 C．既是奇函数又是偶函数 D．非奇非偶函数

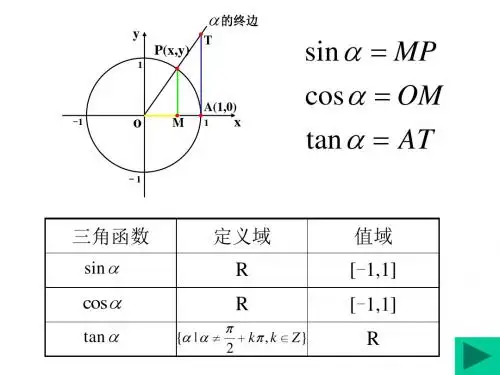
高一数学春季班（教师版）教师日期学生课程编号课型同步复习课课题正弦、余弦函数图像及其性质教学目标1．理解正弦、余弦函数的概念以及图像；2．掌握其奇偶性、单调性、值域及最值；3．学会从研究函数的角度解决实际问题．教学重点1．掌握正余弦函数的各种性质及应用；2．学会从多个角度分析函数．教学安排版块时长1 知识梳理102 例题解析603 巩固训练304 师生总结205 课后练习30 ……1、正弦线：设任意角α的终边与单位圆相交于点),(y x P ，过P 作x 轴的垂线，垂足为M ，则有MP ry==αsin ，向线段MP 叫做角α的正弦线. 2、用单位圆中的正弦线作正弦函数x y sin =，]2,0[π∈x 的图象（几何法）：y=sin x, x ∈[0, 2π]M 1P 1M 2P 2M 1’P 1’M 2’P 2’1-1π2π xyO 2π32π'O3、用五点法作正弦函数的简图（描点法）：正弦函数x y sin =，]2,0[π∈x 的图象中，五个关键点是：)0,0( )1,2(π )0,(π )1,23(-π)0,2(π4、正弦函数R x x y ∈=,sin 的图像：把x y sin =，]2,0[π∈x 的图象，沿着x 轴向右和向左连续地平行移动，每次移动的距离为π2，就得到R x x y ∈=,sin 的图像，此曲线叫做正弦曲线。

正弦、余弦函数的图像与性质知识梳理由正弦函数图像可知： （1）定义域：R（2）值域：[]1,1- ； 正弦线的长度小于或等于单位圆的半径的长度，所以1|sin |≤x ， 即1sin 1≤≤-x ，也就是说，正弦函数的值域是]1,1[-亦可由正弦图像直接得出。

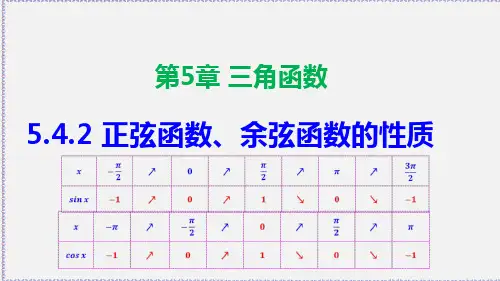
（3）奇偶性：奇函数由x x sin )sin(-=-可知：x y sin =为奇函数，正弦曲线关于原点O 对称 （4）单调递增区间：z k k k ∈⎥⎦⎤⎢⎣⎡+-,22,22ππππ； （5）单调递减区间：z k k k ∈⎥⎦⎤⎢⎣⎡++,232,22ππππ； （6）对称中心：（0,πk ）； （7）对称轴：2ππ+=k x（8）最值：当且仅当,22ππ+=k x y 取最大值1max =y ；当且仅当,232ππ+=k x y 取最小值1min -=y 。

y
π 2

2 1 O -1 -2
y 2 sin x, x R
3p 2
y sin x, x R
3p 2p
5p 2 7p 2
π 2
p
4p
x
1 y sin x, x R 2
1 例2 画出函数 y sin 2 x, x R, y sin x, x R的简图 2 2π 解函数y sin 2 x, x R的周期T 2
2 函数y sin x, x R的周期是什么? 3 它的图像与正弦曲线有什么关系？
一般地函数 y sin x, x R其中 0且 1 的图像. 可以看作把正弦曲线上 所有点的横坐标 缩短（当 1时）
或伸长（当0 1时 ） 到原来的
1
而得到,所以函数 y sin x, x R的值域是
3p 2p
5p 2 7p 2
ห้องสมุดไป่ตู้
π 2
p
4p
x
下面我们一起来研究函 数y sin x, x R和函数y 2 sin x, x R 1 以及函数 y sin x, x R和函数 y sin x, x R图像的关系 . 2
1 y sin x, x R 2
一般地函数 y A sin x, x R其中A 0且A 1 的图像 伸长 可以看作把正弦曲线上 所有点的纵坐标 （当A 1时） （当0 A 1时 ） 到原来的A倍 （ 横坐标不变 ） 或缩短 而得到. 所以函数y A sin x, x R的值域是 [-A,A] ，
单位长度 , 就可以得到正弦函数 .
例1 画出函数y 2 sin x, x R , 1 y sin x, x R的简图 2 解 : 这两个函数的周期都是 2π 我们先画出它们在 0,2π上的简图